Unit 3
Wave nature of particles and the Schrodinger’s equation
Quantum mechanics, science dealing with the behaviour of matter and light on the atomic and subatomic scale. It attempts to describe and account for the properties of molecules and atoms and their constituents—electrons, protons, neutrons, and other more esoteric particles such as quarks and gluons. These properties include the interactions of the particles with one another and with electromagnetic radiation (i.e., light, X-rays, and gamma rays)
Postulate of quantum mechanics:
1. Associated with any particle moving in a conservative field of force is a wave function which determines everything that can be known about the system
2. With every physical observable q there is associated an operator Q, which when operating upon the wave function associated with a definite value of that observable will yield that value times the wavefunction.
3. Any operator Q associated with a physically measurable property q will be Hermitian
4. The set of eigenfunctions of operator Q will form a complete set of linearly independent functions.
5. For a system described by a given wavefunction, the expectation value of any property q can be found by performing the expectation value integral with respect to that wavefunction.
6. The time evolution of the wavefunction is given by the time dependent Schrodinger equation
Louis de- Broglie in 1924 extended the wave particle parallelism of light radiations to all the fundamental entities of Physics such as electrons, protons, neutrons, atoms and molecules etc. He put a bold suggestion that the correspondence between wave and particle should not confined only to electromagnetic radiation, but it should also be valid for material practices, i.e. like radiation, matter also has a dual (i.e., particle like and wave like) character.
A moving particle is always associated with the wave and the particle is controlled by waves. This suggestion was based on the fact that nature loves symmetry, if radiation like light can act like waves some times and like a particle at other times, then the material particles (e.g., electron, neutrons, etc.) should act as waves at some other times. These waves associated with particles are named de- Broglie waves or matter waves.
Louis de- Broglie in 1924 extended the wave particle parallelism of light radiations to all the fundamental entities of Physics such as electrons, protons, neutrons, atoms and molecules etc. He put a bold suggestion that the correspondence between wave and particle should not confined only to electromagnetic radiation, but it should also be valid for material practices, i.e. like radiation, matter also has a dual (i.e., particle like and wave like) character.
A moving particle is always associated with the wave and the particle is controlled by waves. This suggestion was based on the fact that nature loves symmetry, if radiation like light can act like waves some times and like a particle at other times, then the material particles (e.g., electron, neutrons, etc.) should act as waves at some other times. These waves associated with particles are named de- Broglie waves or matter waves.
Expression for de- Broglie wavelength
The expression of the wavelength associated with a material particle can be derived on the analogy of radiation as follows:
Considering the planck's theory of radiation, the energy of photon (quantum) is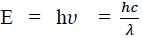 
Where c is the velocity of light in vacuum and is its wavelength.
According to Einstein energy – mass relation
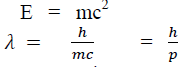
Where mc = p is momentum associated with photons.
If we consider the case of material particle of mass m and moving with a velocity v, i.e. momentum mv, then the wavelength associated with this particle ( in analogy to wavelength associated with photon ) is given by
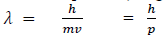
Different expressions for de-Broglie wavelength
(a) If E is the kinetic energy of the material particle then
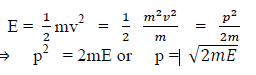
There for de Broglie wavelength is—
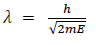
(b) When a charged particle carrying a charge ‘q’ is accelerated by potential difference v, then its kinetic energy K.E is given by
E = qV
Hence the de-Broglie wavelength associated with this particle is
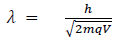
For an electron
Time dependent equation:
It was observed that the wave function of a particle of fixed energy E could most naturally be written as a linear combination of wave functions of the form:
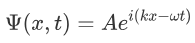
Now the hemiltonian of this system:
H=T+V
Where V is the potential energy and T is the kinetic energy. As we already know that ‘H’ is the total energy, we can rewrite the equation as:
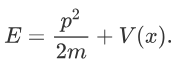
Now taking the derivatives:
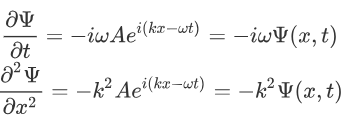
We know that:
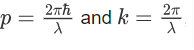
Where ‘λ’ is the wavelength and ‘k’ is the wavenumber.
We have:
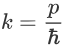
Therefore:
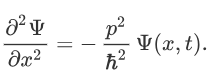
Now multiplying Ψ (x, t) to the Hamiltonian we get:
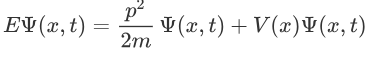
The above expression can be written as:
We already know that the energy wave of a matter wave is written as:
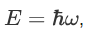
So, we can say that
Now combining the right parts, we can get the Schrodinger Wave Equation.
Time independent equation:
According to de-Broglie theory, for a particle of mass ‘m’, moving with a velocity ‘v’, the wavelength associated with it is
λ=h/p
The wave equation for a de-Broglie wave can be written in complex notation as:
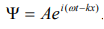…………1
Where, A is the amplitude, ω is angular frequency and k is the wave vector.
Differentiate equation (1) with respect to ‘t’ twice, we get
We have differential equation for the traveling wave as,
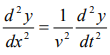……….3
Where, y is displacement and ‘v’ is velocity of wave.
By analogy, we can write the wave equation for de-Broglie wave associated with the motion of a free particle as,
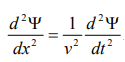………4
This represents the de-Broglie wave propagating along x-direction with a velocity ‘v’ and ‘Ψ’ is the displacement.
From equation (2) and (4),
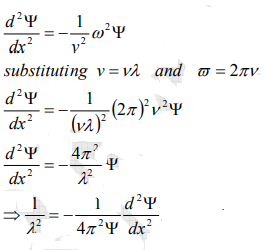…………..5
The kinetic energy of a moving particle of mass ‘m’ and velocity ‘v’ is given by
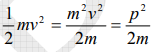
But we have from equation (1), p = (h/λ)
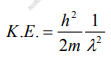
Substitute for (1/ λ)2 from equation (5),
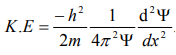…………….6
Let there be a field where the particle is present. Depending on its position in the field, the particle will possess certain potential energy. Then we can write:
Total energy = Kinetic energy + Potential energy
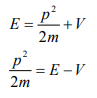
From equation (6), we can write
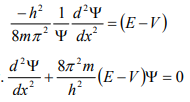
This is the time independent Schrödinger’s wave equation in one-dimension.
We will now look at the solutions of a particle of mass m confined to move along the x-axis between 0 to L. This is achieved by making the potential 0 between x = 0 and x = L and V = ∞ for x < 0 and x > L. In quantum mechanics this model is referred to as a particle in a box (PIB) of length L.
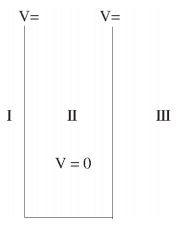
The one-dimensional infinite potential well of length L. It is divided into three regions, with regions I and III having V = ∞ and region II having V = 0
Before we set up and solve the Schrodinger equation let us apply de Broglie’s approach to this problem. De Broglie associates a wave with every material particle traveling with momentum p. The wavelength of the wave is
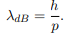
The classical analog of a particle in a box is a string that is fixed at both ends. When such a string is plucked, we know that the amplitude of the oscillations at the fixed ends is zero. In other words, an integer number of half-wavelengths must fit in the length of the box. Applying this idea to the present case, we find that
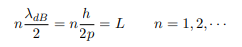
Solving for p we get
The particle feels no potential energy so all its energy is in the form of kinetic energy. As a result
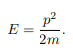
Substituting for p, we get
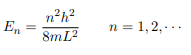
The Schrodinger equation is-
Hψˆ (x) = Eψ(x)
Where V (x) = ∞ in regions I and III and V (x) = 0 in region II. The results are in no way affected if in region II the potential is V because it only has the effect of altering the zero of energy and so without generality, we will assume that V = 0 within the box. In regions I and III the wave function is identically zero since the potential is infinite so we will only have to consider the solution within the box. We are looking for the solutions to the equation.
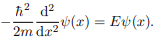
We rewrite this differential equation in the form:
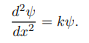
Wave equation
ψ(x) = A cos(kx) + B sin(kx)
The boundary conditions that the wave function should satisfy are
ψ (0) = 0 and ψ(L) = 0. The
First of these conditions implies that A = 0.
The second condition yields
B sin(kL) = 0
Which implies that kL = nπ, n = 1, 2, 3, · · ·
Or in other words k = nπ/L. Because E is related to k we hence obtain that
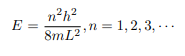
You will notice that the application of the boundary conditions naturally leads to quantization. In addition, observe that we do not consider n = 0 as a possibility because that would imply that the wave function is identically zero for all x or in other words there is no particle! The constant B is yet to be determined. The normalization condition on the wave function yields B.
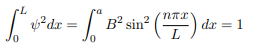
In cases where the wave function is not an eigenfunction of the operator corresponding to the observable, we will be concerned with the statistical mean of the measured values, averaged over a large number of measurements, the expectation value. The expectation value is defined of an operator is defined a:
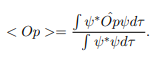
The average momentum is the
According to this theory, a metal consists of electrons which are free to move about in the crystal-like molecules of a gas in a container. Mutual repulsion between electrons is ignored and hence potential energy is taken as zero. Therefore, the total energy of the electron is equal to its kinetic energy. This model provided a satisfactory explanation for certain properties (e.g electrical conductivity, electronic emission and electronic emission) but failed to explain why some solids are good conductors, some are semiconductors and others are insulators. It also fails to explain the specific heat of metals and magnetic susceptibility of paramagnetic metals.
This theory was developed by Drude and Lorentz and hence is also known as Drude-Lorentz theory.
Postulates of free electron Model
1. The outermost electrons of the constituent atom of the metal are weakly bound with the atoms. Hence these electrons get separated from their atoms and move freely inside the substance and are called free electrons.
2. There are a large number of free electrons inside the metals and they behave like molecules of a gas enclosed in a container. Hence it is called free electron gas. These free electrons are responsible for the thermal and electrical conduction inside the metal. Hence, they are also called conduction electrons.
3.The free electrons in thermal equilibrium obey Maxwell-Boltzmann statistics. Which states that the free energy per electron at an absolute temperature T is 1/2 KT, where K is Boltzmann's constant.
4. Inside the metal, free electrons move randomly with high velocity and it depends on the temperature of the metal. During the motion, their velocity and direction changes in such a way that the rate of flow of electrons in a particular direction is zero.
5. When the metal is kept in an external electric field, the free electrons gets attracted in the direction opposite to the direction to the external electric field. They start moving with a constant average velocity called drift velocity.
The highest energy level that an electron can occupy at the absolute zero temperature is known as the Fermi Level. The Fermi level lies between the valence band and conduction band because at absolute zero temperature the electrons are all in the lowest energy state.
In a p type semiconductor, there is an increase in the Density of unfilled States. Thus, more electrons can be accommodated at lower energy states. In a n type semiconductor, the DOS is increased. Thus, electrons have to be accommodated at higher energy levels.
Fermi level is also defined as the work done to add an electron to the system. More positive (more holes) in a p type semiconductor, mean lesser work needs to be done. Hence a lower Fermi level.
The density of states in a semiconductor equals the number of states per unit energy and per unit volume.
Calculation of Density of states
We will assume that the semiconductor can be modelled as an infinite quantum well in which electrons with effective mass, m*, are free to move. The energy in the well is set to zero. The semiconductor is assumed to be a cube with side L.
This assumption does not affect the result since the density of states per unit volume should not depend on the actual size or shape of the semiconductor.
Consider a sphere in k-space. Associated with this sphere volume will be
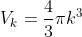
Where k is our “radius" where
We now define a state by the smallest nonzero volume it possesses in k-space. This occurs when
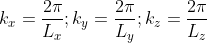
A cube in k-space with size L (Lx = Ly = Lz =L) as indicated on Figure
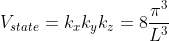
Thus, within our imagined spherical volume of k-space, the total number of states present is
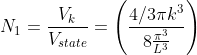
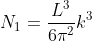
Next, when dealing with electrons and holes, we must consider spin degeneracy, since two carriers, possessing opposite spin, can occupy the same state. As a consequence, we multiply the above expression by 2 to obtain
Density of states is number of states per unit volume per unit energy range, therefore dividing N with volume (L3) and differentiating it with respect to E
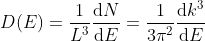
Or
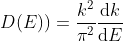
As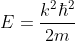 
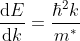
Or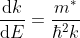 
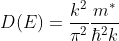
Or
This is our desired density-of-states expression for a bulk three dimensional solid.
The Bloch theorem in essence formulates a condition that all solutions ψk(r), for any periodic potential V(r) whatsoever, have to meet. In one version it ascertains
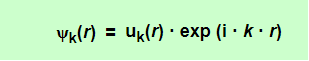
With k = any allowed wave vector for the electron that is obtained for a constant potential, and uk(r) = arbitrary functions (distinguished by the index k that marks the particular solution we are after), but always with the periodicity of the lattice, i.e.
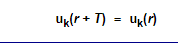
Any wavefunction meeting this requirement we will henceforth call a Bloch wave
The Bloch theorem is quite remarkable, because, as said before, it imposes very special conditions on any solution of the Schrödinger equation, no matter what the form of the periodic potential might be.
We notice that exactly as in the case of the constant potential, the wave vector k has a twofold role: It is still a wave vector in the plane wave part of the solution, but also an index to ψk(r) and uk(r) because it contains all the quantum numbers, which enumerate the individual solutions.
Bloch's theorem is a proven theorem with perfectly general validity. We will first give some ideas about the proof of this theorem, and then discuss what it means for real crystals. As always with hindsight, Bloch's theorem can be proved in many ways
It follows rather directly from applying group theory to crystals. In this case one looks at symmetry properties that are invariant under translation
It can easily be proved by working with operator algebra in the context of formal quantum theory mathematics
It can be directly proved in simple ways – but then only for special cases or with not quite kosher "tricks".
It can be proved (and used for further calculations), by expanding V(r) and ψ(r) into a Fourier series and then rewriting the Schrödinger equation. This is a particularly useful way because it can also be used for obtaining specific results for the periodic potential
Bloch's theorem can also be rewritten in a somewhat different form, giving us a second version:
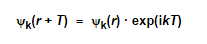
This means that any function ψk(r) that is a solution to the Schrödinger equation of the problem, differs only by a phase factor exp(ikT) between equivalent positions in the lattice
This implies immediately that the probability of finding an electron is the same at any equivalent position in the lattice, exactly as we expected, because
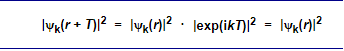
This is so because |exp(ikT)|2 = 1 for all k and T.
If we write the wave function in the first form ψk(r) = uk(r) · exp(ikr) and consider its value at an equivalent lattice position r + T we obtain |
|
Bloch's theorem has many more forms and does not only apply to electrons in periodic potentials, but for all kinds of waves, e.g. Phonons. However, we will now consider the theorem to be proven and only discuss some of its implications.
According to quantum free electron theory of metals, a conduction electron in a metal experiences constant (or zero) potential and free to move inside the crystal but will not come out of the metal because an infinite potential exists at the surface. This theory successfully explains electrical conductivity, specific heat, thermionic emission and Para magnetism. This theory is fails to explain many other physical properties, for example:
(i) it fails to explain the difference between conductors, insulators and semiconductors,
(ii) positive Hall coefficient of metals and
(iii) lower conductivity of divalent metals than monovalent metals.
To overcome the above problems, the periodic potentials due to the positive ions in a metal have been considered., if an electron moves through these ions, it experiences varying potentials. The potential of an electron at the positive ion site is zero and is maximum in between two ions. The potential experienced by an electron, when it passes along a line through the positive ions
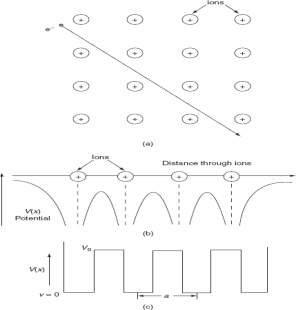
It is not easy to solve Schrödinger’s equation with these potentials. So, Kronig and Penney approximated these potentials inside the crystal to the shape of rectangular steps as shown in Fig. (c). This model is called the Kronig-Penney model of potentials.
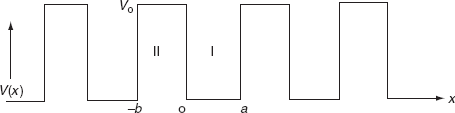
The energies of electrons can be known by solving Schrödinger’s wave equation in such a lattice. The Schrödinger time-independent wave equation for the motion of an electron along X-direction is given by:
...............(1)
The energies and wave functions of electrons associated with this model can be calculated by solving time-independent one-dimensional Schrödinger’s wave equations for the two regions I and II as shown in Fig
The Schrödinger’s equations are:
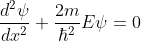for 0<x<a.............(2)
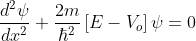for -b<x<0.............(3)
We define two real quantities (say) α and β such that:
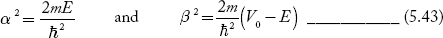
Hence, becomes:
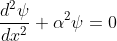for 0<x<a
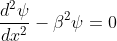for -b<x<0
According to Bloch's theorem, the wave function solution of the Schrödinger equation when the potential is periodic and to make sure the function u(x) is also continuous and smooth, can be written as:
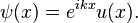
Where u(x) is a periodic function which satisfies u (x + a) = u(x).
Using Bloch theorem and all the boundary conditions for the continuity of the wave function the solution of Schrodinger wave equation obtained as
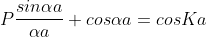
Where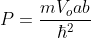 
This equation shows the relation between the energy (through α) and the wave-vector, k, and as you can see, since the left hand side of the equation can only range from −1 to 1 then there are some limits on the values that α (and thus, the energy) can take, that is, at some ranges of values of the energy, there is no solution according to these equation, and thus, the system will not have those energies:
Energy gaps. These are the so-called band-gaps, which can be shown to exist in any shape of periodic potential (not just delta or square barriers).
1. The permissible limit of the term
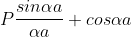
Lies between +1 to -1. By varying αa, a wave mechanical nature could be plotted as shown in Fig, the shaded portion of the wave shows the bands of allowed energy with the forbidden region as unshaded portion.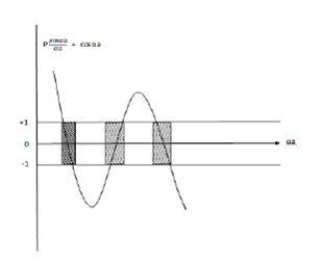
2. With increase of αa, the allowed energy states for an electron increases thereby increasing the bandwidth of the bands, i.e., the strength of the potential barrier diminishes. This also leads to an increase of the distance between electrons and the total energy possessed by the individual electron.
3.Conversly if suppose the effect of potential barrier dominate i.e., if P is large, the resultant wave obtained in terms of 
shows a stepper variation in the region lies between +1 to -1. This results in the decrease of allowed energy and increase of forbidden energy gap. Thus, at extremities,
Case (i) when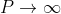 
, the allowed energy states are compressed to a line spectrum.
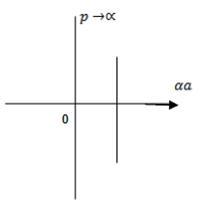
Case (ii) when 
The energy band is broadened and it is quasi continuous.
In an isolated atom, the electrons are tightly bound and have discrete, sharp energy levels [Figure]. When two identical atoms are brought closer, the outermost orbits of these atoms overlap and interact. When the wave functions of the electrons of the different atoms begin to overlap considerably, the energy levels split into two
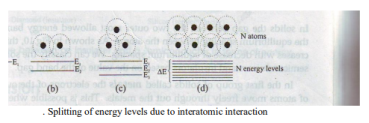
If more atoms are brought together, more levels are formed and for a solid of N atoms, each of the energy levels of an atom splits into N levels of energy [Figure]. The levels are so close together that they form an almost continuous band. The width of this band depends on the degree of overlap of the electrons of adjacent atoms and is largest for the outermost atomic electrons. In a solid, many atoms are brought together that the split energy levels form a set of energy bands of very closely spaced levels with forbidden energy gaps between them. Overlapping of these atoms occurs for smaller equilibrium spacing.
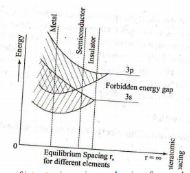
The band corresponding to outermost orbit is called conduction band and the next band is called valence band. The gap between these two allowed bands is called the forbidden energy gap or band gap. According to the width of the gap between the bands and band occupation by electrons all solids can be classified broadly into three groups namely, conductors, semiconductors and insulators.
