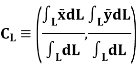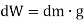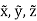Unit - 4
Centroid and Centre of Gravity
Center of Line:
Consider a line defined by a curve y = f(x) lies in a x-y plane as shown in figure.
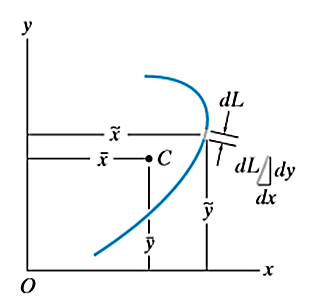
Now, consider a small element dL whose center is located at (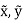 ) in the x-y reference frame.
) in the x-y reference frame.
Then, the center of whole line is formulated by integration shown below
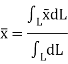
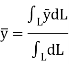
Hence, the location of center of line is given as
Center of Area (Centroid)
Consider a small vertical strip of planar body bounded by a curve y = f(x) in x-y plane as shown in figure.
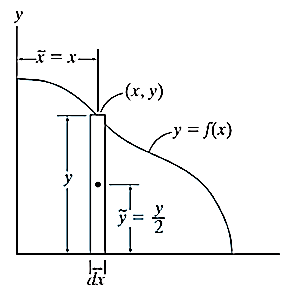
Let the center of the vertical strip be located at (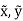 ) in the x-y reference frame and dA be the area of strip.
) in the x-y reference frame and dA be the area of strip.
Then, the center of whole area (centroid) is formulated by integration shown below

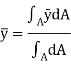
Hence, the location of center of area or centroid of area body is given as
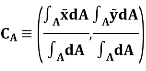
Let the planar body of area A is made up of n number of small elements of area A1, A2, A3, …, An whose center is located at a distance of x1, x2, x3, …, xn from y-axis and y1, y2, y3, …, yn from x-axis.
Then according to first principle, the centroid of a planar body is given by,
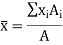
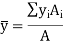
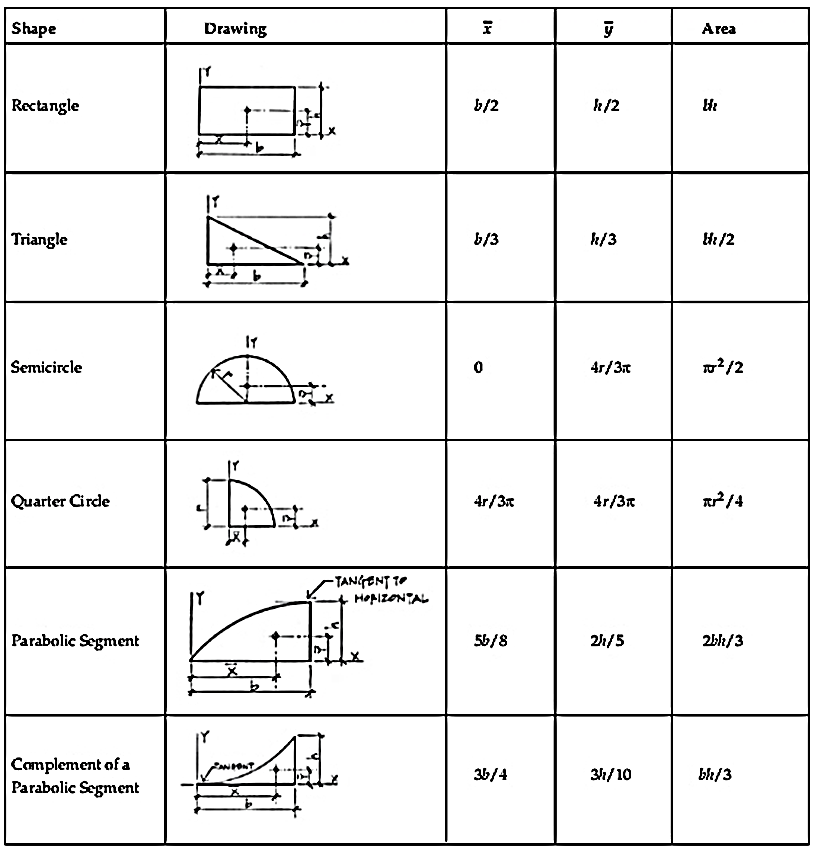
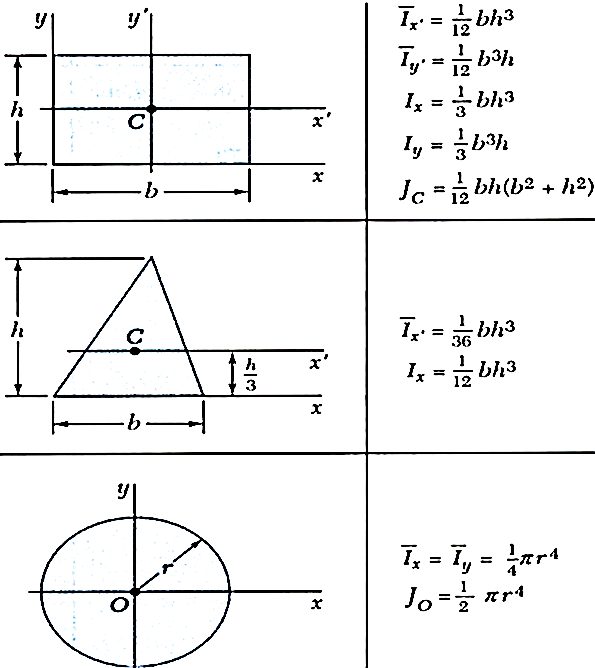
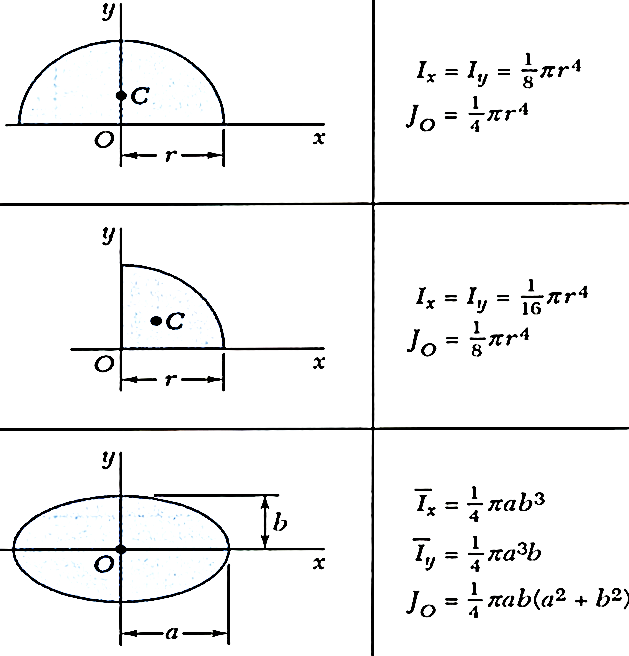
Centroid of some simple figures is tabulated below:
First principal is used to find the centroid of the composite sections.
Consider the I section shown below. I section can be broken down into three rectangles as shown.
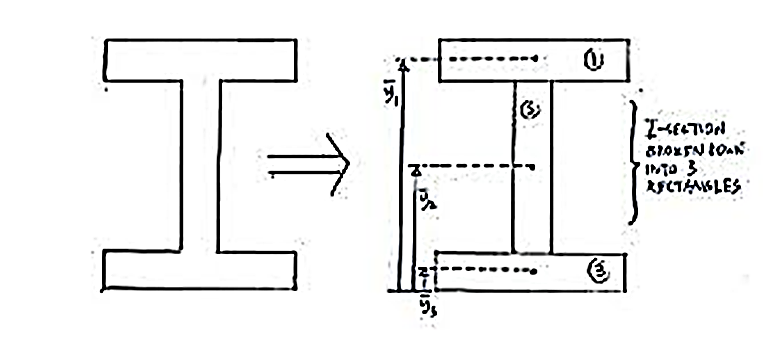
As I section is symmetric about y axis, hence, 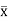 will be at the mid-plane of the section.
will be at the mid-plane of the section.
To find  first principal is used.
first principal is used.
Let the area of rectangles 1, 2 and 3 from figure be A1, A2 and A3 respectively.
Let 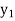 ,
, 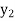 and
and 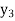 be the distance between x-axis and the centroids of the rectangles 1, 2 and 3 respectively.
be the distance between x-axis and the centroids of the rectangles 1, 2 and 3 respectively.
Then, according to first principle,
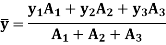
Hence, for the composite sections, made from n number of elements with area A1, A2, A3, …, An whose center is located at a distance of x1, x2, x3, …, xn from y-axis and y1, y2, y3, …, yn from x-axis.
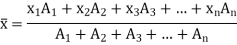
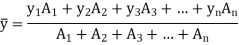
Hence, the centroid of composite sections is given by,
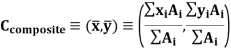
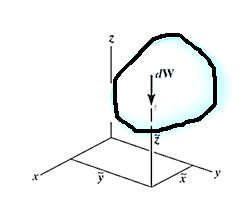
Let, 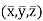 be the location of center of gravity CG of the body.
be the location of center of gravity CG of the body.
Weights of each particle will form an approximately parallel force system, and the resultant of this system is the total weight of the body W, which passes through a single point called the center of gravity G.
i.e., the weight of the body is the sum of the weights of all of its particles
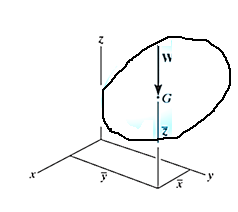
Now, the moment of W about x-axis is equal to the sum of moment of weights of each particle about same axis.
We get,
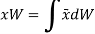
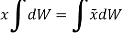
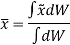
Similarly, if moments are summed about the y axis,
We get,
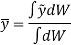
Now, consider that the body is fixed within the coordinate system and this system is rotated about the y axis as shown in fig
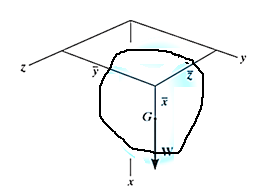
In similar manner, if moments are summed about the z axis, we get,
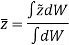
Hence, the location of center of gravity with respect to x, y, z axes is
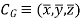
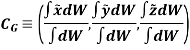
Implication of center of gravity: Center of gravity and center of mass of a body is equal. Because, As, W = mg.
Hence,
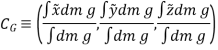
As g is constant,
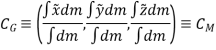
Hence, the conclusion is, center of gravity and center of mass coincides.
Definition:
Explanation:
Consider a differential plate, subjected to fluid pressure P that varies linearly with depth, as shown in fig, such that 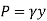 , where,
, where, 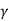 is the specific weight of fluid.
is the specific weight of fluid.
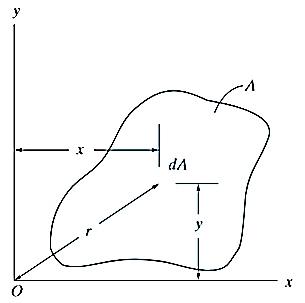
The force acting on an acting on the differential area of the plate is given by
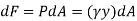
The moment of this this force about the x-axis is
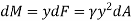
Integrating 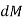 over the entire area of the plate yields
over the entire area of the plate yields
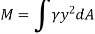
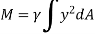
The integral part of the moment equation is called area moment of inertia about x-axis 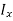
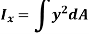
Similarly, area moment of inertia about y-axis is given as,
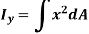
Radius of gyration:
Moment of Inertia for area can also be given as
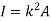
Where, A is the total area
And k is referred as radius of gyration
Radius of gyration for area of a plate about an axis is defined as the radial distance to a point which would have a same moment of inertia as the plate’s actual distribution of area, if the total area of the plate were concentrated.
It is given by,
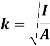
Moment of inertia of rectangle:
Consider a rectangular area of width b and depth d as shown in figure.
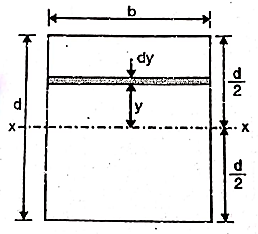
Consider an elemental strip of thickness dy parallel to x-x at a distance y from x-x.
Area of elemental strip = b dy
By definition of moment of inertia,
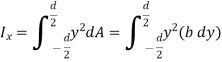
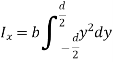
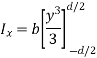
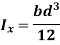
Similarly,
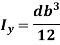
According to theorem of parallel axes.
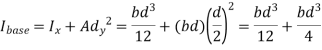
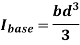
Theorem of Parallel Axes:
Mathematically,
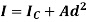
Where, 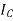 is the moment of inertia about axis passing through the centroid, and d is the perpendicular distance between two axes.
is the moment of inertia about axis passing through the centroid, and d is the perpendicular distance between two axes.
Proof:
For the system shown below,
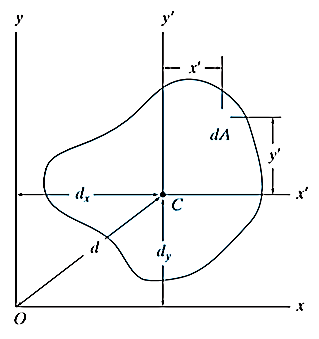
By definition of Moment of inertia,
Moment of inertia about axis x’ passing from center of gravity C is
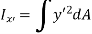
Moment of inertia about x-axis is
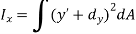
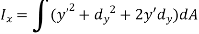
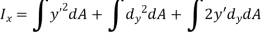
But,
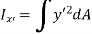
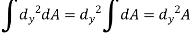
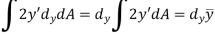
And as 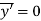 (distance between centroid and x’ axis.
(distance between centroid and x’ axis.
Hence,
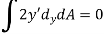
Therefore,
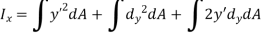
Becomes,
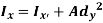
Similarly,
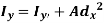
It states that, “For a planar body, the sum of moments of inertia about two mutually perpendicular axes in the plane of the body is equal to the moment of inertia about an axis perpendicular to the plane of the body.”
Mathematically,
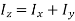
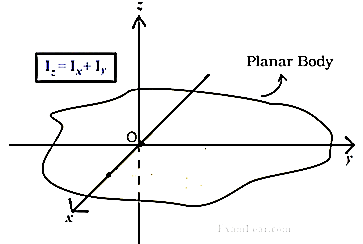
Proof:
Consider a body shown in figure,
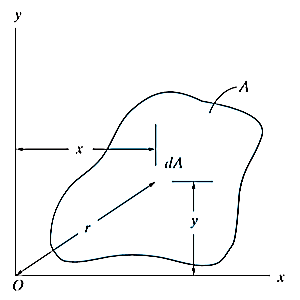
According to definition of moment of inertia,
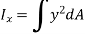
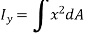
From figure,
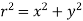
Now, according to definition, moment of inertia about an axis perpendicular to plane of body and passing through O is,
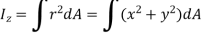
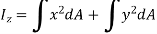
Hence,
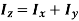
Moment of inertia about the axis perpendicular to plane or any cross-section is called as polar moment of inertia. Denoted by J.
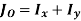
Moments of inertia of some standard sections is tabulated below:
Moment of Inertia for composite sections:
A composite area consists of a series of connected “simpler” parts or shapes, such as rectangles, triangles and circles. Provided the moment of inertia of each of these parts is known or can be determined about a common axis, then the moment of inertia for the composite area about this axis equals the algebraic sum of the moments of inertia of all its parts.
Consider a composite section made of n number of different standard sections with moment of inertia about an axis of 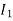 ,
, 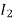 , …,
, …, 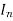 .
.
Then, the moment of inertia of a composite section about an axis is equal to the algebraic sum of moments of inertia of individual component about same axis.
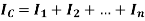
Moment of Inertia of triangle
Consider a triangular area of width b and height h as shown in figure.
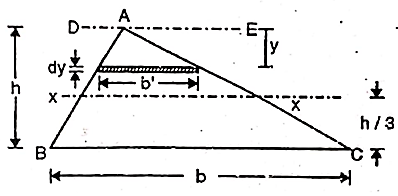
Consider an elemental strip of thickness dy parallel to x-x at a distance y from apex A
Area of elemental strip = b’ dy
From figure,
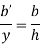
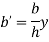
Area = 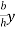
By definition of moment of inertia,
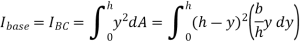
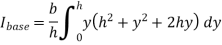
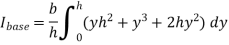
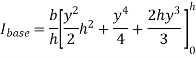
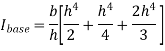
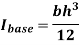
According to theorem of parallel axes.
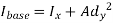
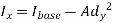
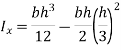
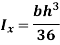
Moment of Inertia of Circle:
Consider a circle of diameter d as shown in figure.
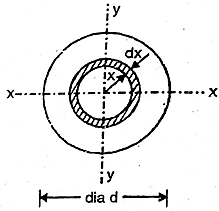
Consider an elemental ring at distance x from OZ axis perpendicular to plane x-y at center O and of thickness dx.
Area of elemental ring = (2πx) dx
By definition of moment of inertia,
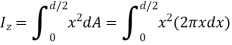
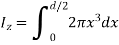
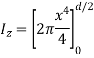
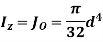
As circle is symmetric about x and y axis, hence, 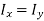
According to perpendicular axes theorem,
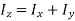
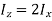
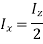
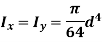
Mass moment of Inertia for circular plate:
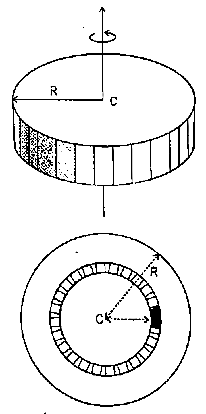
Consider an elemental strip of mass dm at distance r from CZ axis perpendicular to plane of circular plate at center C and of thickness dr.
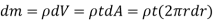
By definition of moment of inertia,
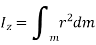
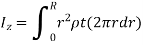
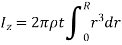
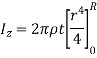
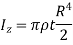
For a circular plate,
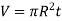 and
and 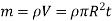
Hence,
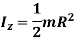
As a circular plate is symmetric about x and y axis, hence, 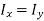
According to perpendicular axes theorem,
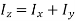
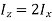
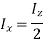
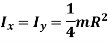
Mass moment of inertia of cylinder:
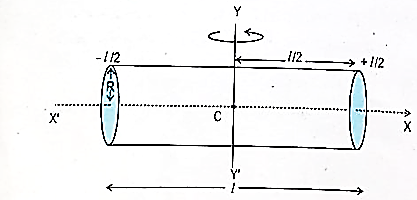
Consider a long cylinder rotating about z- axis of height h and radius r as shown in figure.
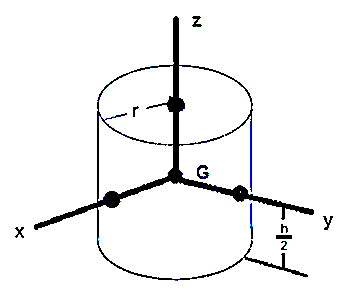
Cylinder is nothing but a combination of number of small circular plates piled one above another. And as moment of inertia about z- axis does not depend on the thickness of circular plate. Hence, M.I. of cylinder about z-axis is equal to that of M.I. of circular plate about z-axis.
Hence, for cylinder,
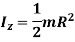
Now, consider a cylinder rotating about an axis perpendicular to geometric axis (z-axis)
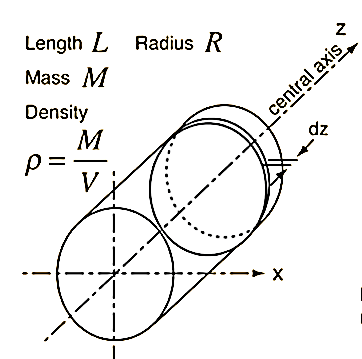
Consider a small elemental disc of mass dm of thickness dz at a distance of z from CG.
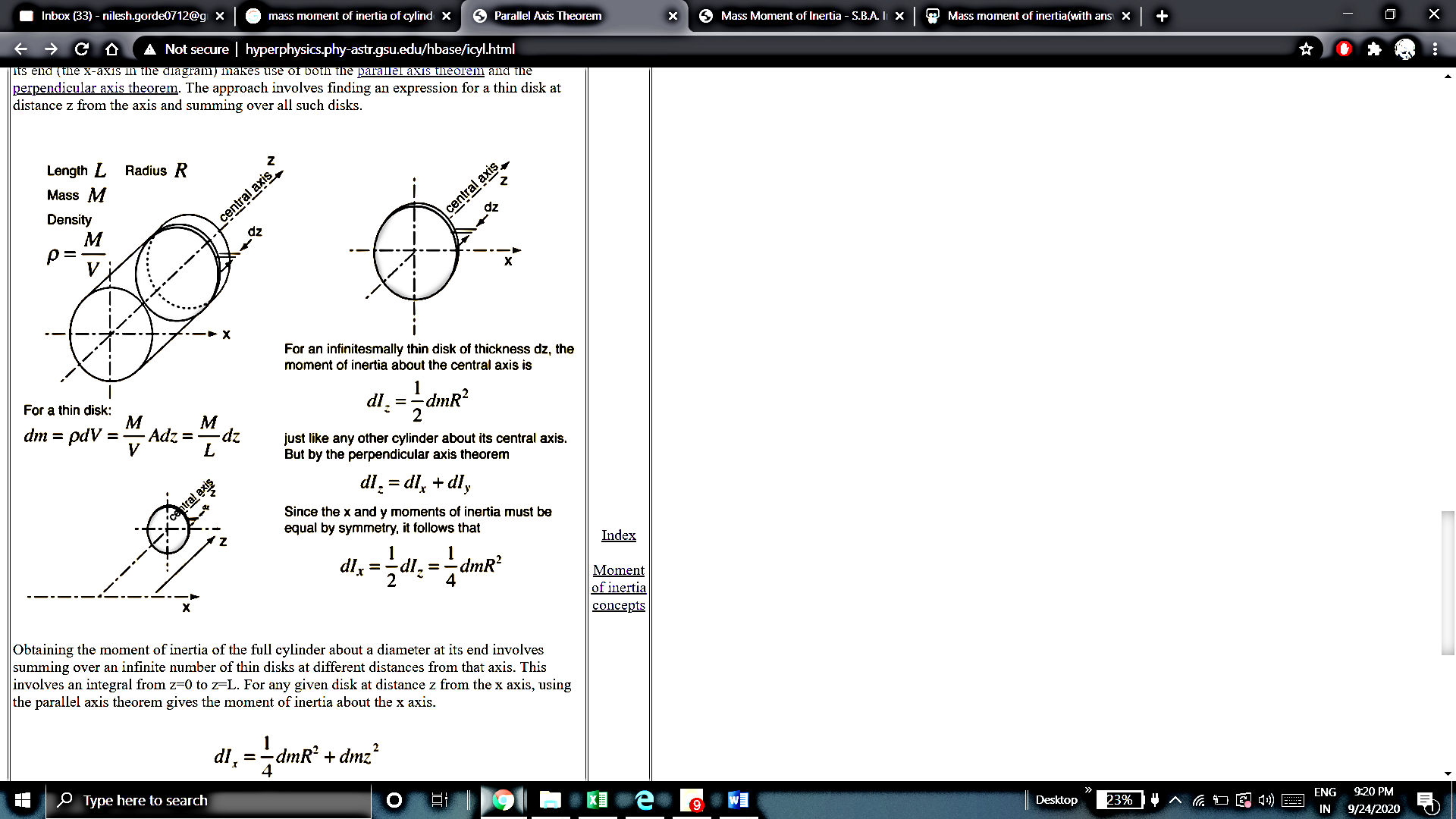
Moment of inertia about central axis is given as,
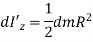
By, perpendicular axes theorem,
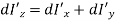
Since, 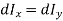 due to symmetry,
due to symmetry,
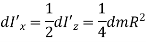
Now, mass of elemental plate is
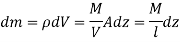
Where, M is the total mass of cylinder, V is the volume of cylinder and L is the total length of cylinder.
Now, as the elemental disc is at a distance of z from the CG of the cylinder,
According to parallel axes theorem,
Moment of inertia of a disc about an axis passing through CG of cylinder is
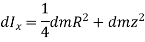
Moment of inertia rotating about an axis perpendicular to geometric axis (z-axis) of cylinder is found by integrating above equation.
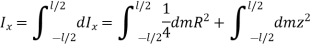
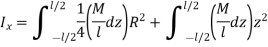
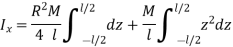
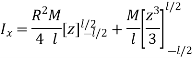
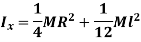
Moment of Inertia of cone:
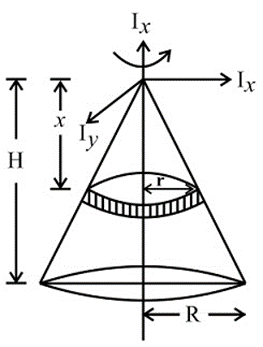
Consider a small strip of mass dm, radius r at a distance x and thickness dx from the apex.
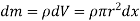
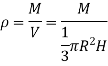
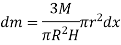
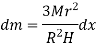
Now, from figure, we have,
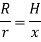
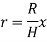
Hence,
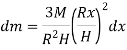
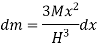
Now, moment of inertia of elemental disc about vertical axis is
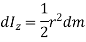
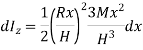
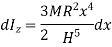
Moment of Inertia about geometric axis of cone is given by integrating above equation
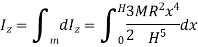
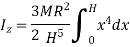
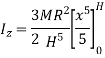
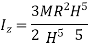
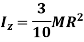
Moment of Inertia of sphere
Consider a sphere of radius R and mass M as shown in figure below.
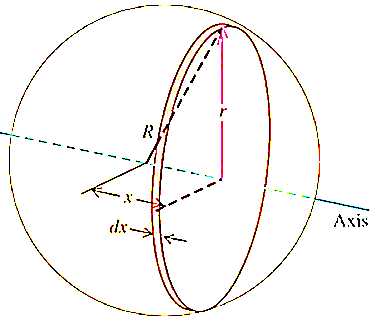
Consider a small elemental plate of mass dm, thickness dx, radius r at a distance of x from the center of sphere.
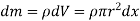
Moment of inertia of the elemental strip is,
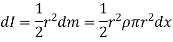
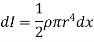
Now, from figure,
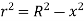
Hence,
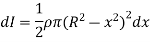
Moment of inertia of whole sphere is found by integrating moment of inertia of small elemental strip from radius -R to R
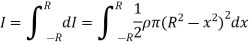
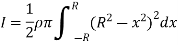
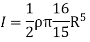
Now, we have,
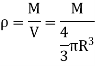
Hence, we get,
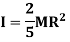
References:
1. Irving H. Shames (2006), Engineering Mechanics, 4th Edition, Prentice Hall
2. F. P. Beer and E. R. Johnston (2011), Vector Mechanics for Engineers, Vol I - Statics, Vol II, – Dynamics, 9th Ed, Tata McGraw Hill
3. R. C. Hibbler (2006), Engineering Mechanics: Principles of Statics and Dynamics, Pearson Press.
4. Andy Ruina and Rudra Pratap (2011), Introduction to Statics and Dynamics, Oxford University Press
5. Shanes and Rao (2006), Engineering Mechanics, Pearson Education