MODULE 1

Sets, Relation And Function

1.1             TYPES OF SETS

                           Finite : A set which has finite dement is called finite set e.g. {1, 2, 3 }

                           Infinite Set: A set which is not finite is called Infinite set. e.g. {1, 2, 3 ……}

                           Null set : A set having no elements is called null set. e.g. {    }

  Universal Set : The universal set is denoted by U or S. If we are studying sets of real numbers, then universal set it will be set of all real numbers.

  Subset : Given two set A & B if every element of A is an element of B then A is called a subset of B.  A  B.

  Equality of sets If every element of A is an element B & if every element B is an element of A, then the set is equal to set B.If A B & if B  A then A =B.

  Complement of Set: The set of all elements of U which do not belong to A is called complement of A.

  Union of Sets:  The union of two sets A & B is defined as the set of all elements which we either A or in B.A B = {x/x 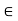A or 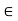B or both}

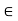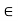  Intersection of sets: Common elements in A & B.  A  B {x/x A & xB }

  De- Morgan Law

1.2 Laws of set:

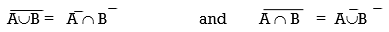
1) Idempotent Law  AA = A  AA = A

2) Identity Law   A = A  AU = A

3) Inverse Law   AA = U  AA = 

4) Domination Law  AU = U  A = 

5) Commutative Law  AB = BA  AB = BA

6) Associate Law  A (BC) = (AB) C

A (BC) = (AB) C

7) Distribution Law  A (BC) = (AB)  (AC)

A (BC) = (AB)  (AC)

8) De-Morgan Law

 AB = A  B

9) Absorption Law  A (AB) = A   A (AB) – A

10) Double Complementation (A) = A

11) If A  B then   AB = A

A B = B

       B  A

12)  A – B =  AB

13) A  B = (AB) – (AB)

14) A B = (A-B)  (B-A)

15) A – B = A B

Q.Eg.1) P.T.  A  B = A  B

 LS  = A  B

  = (A – B)  (B – A)     …….. Formula No. (14)

  = (A B)  (B A) ……… No. (15)

 = (A B)  (B A) ………….

= (B A)  (AB)

= (A – B)  (B-A)

= A  B

Q.2) P.T. A – (BC) = (A-B)  (A-C)

Let x EA – (BC)

 x EA and x  BC

 x EA and x  B  and xC

 x EA and x  B and xA and x/

 x E (A-B) and x E (A-C)

 x E (A-B)  (A-C)

 A- (BC)  (A-B)   (A-C)

Procedure to find No. Of elements in subset.

1. n(A-B) = n (A  B) = n (A) - n (AB)

2. n (B-A) = n (B  A) = n (B) - n (AB)

3. n (AB) = n (A) +  n (B) - n (AB)

4. n (AB) = n (A  B) = n (S) - n (AB)

* When there are three sets

1. n (A-B-C) = n [ A  (BC)] = n [ ABC]

= n (A) - n (AB)  - n (AC) + n [ABC)

2. n (B-A-C) = n [ B  (AC)] = n [B AC]

1. In a class of 60 students 30 students got first class in sem 1 & 25 got first class in sem 2.  If 20 students did not get 1st class in either examination & how many got 1st class in both?

Solution: (S) = 60

(A) = 30

(B) = 25

    (AB) = 20

 (AB) =      (S)    -      (AB)

= 60 – 20

= 40

n (AB) = n (A) + n (B) - n (AB)

= 30 + 25 – 40 = 15

The number of students who got first class in both semester = 15.

1.3  Logic

Symbolizing Statement

1) Negation (p)

2) Conjunction ( p  q)

3) Disjunction (p  q)

4) Implication ( p  q)

a) Converse of p  q is [q p]

b) Inverse of p  q is [  p  q]

c) Contra positive of p  q is [q p]

1.4 Truth Table

1) Negation  p p

T F

F T

2) Conjunction   Disjunction   Implication 

p q   p  q   p  q   p q   p q p q

T T          T   T T      T   T T    T

T F      F   T F       T   T F     F

F T      F   F T     T                              F  T    T

F F          F   F F      F   F F      T

Q. Prove that p  (q r) and (pq)  (p  r) are logically equivalent.

p   q   r     qr  p  (q r) (pq)  (pr)  (pq) V (pr)

T T T T       T    T     T   T

T T F T       T     T     F   T

T F T T       T      F     T    T

T   F F F        F                 F      F     F

F T T T        F       F                F      F

F T T T        F       F                F      F

F T F T        F       F                F      F

F F T T        F       F                F      F

F F F F        F       F                F      F

Tautologies : If the statement or last column is true than its tautology.

Contradiction: If the last column is false that its contradiction.

Contingencies: If the last column is T and F then its contingencies statement.

* Duality:

1) Idempotent Law :-

pp  p   p  p  p

2) Commutative law :-

p q  q p   p  p  qp

3) Associative Law :-

(pq)  r  p (qr)  (pq)  r  p (qr)

4) Identity Law :-

p  t  p   pf  p

5) Domination Law :-

pt  t    pf  f

6) Distribution Law :-

p  (qr)  (pq)  (pr)

7) Complement Law :-

p  p  t    p  p  f

8) Double Negation

 (p)  p    t  f,     f  t

9) De- Morgan Law :

 (p q)  pq  ;  (pq)  p q

10) Absorption Law :

p  (p q)  p  p  (p q)  p

11) Contrapositive  p  q  q  p

12) Conditional   p  q  p  q

14) Biconditional   (p  q)  (p  q)  (q  p)

Q.) Using the law of logic P.T.  (p  q)  (p

 ( p  q)  p  q

L.H.S.  (p  q)   ( p  (pq))

 (p  q)   ( p p) q)        By Association

 (p  q)   ( p q)        [ p  p  p]

 (p  q)  (  p  q)  (Implication)

  (p  q)  ( p  q)  (Double neg

 ( (  p  q)  p)  (( p  q)   (Commutation)

 ( (  p  q)  p)  ( p  q)  

 (t  q)  ( pq)

 p  q

1.5 Cartesian Product:

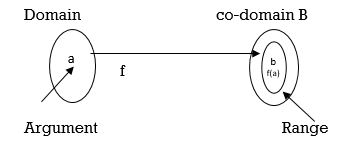
An ordered pair (a,b) is a listing of two objects a & b in given order with a appearing first & b appearing second.

Q.1) Let A = {1, 2 ,3} and B = {1, 2, 3}

Find A X A & A X B

A X B = {1,1}{1,2}{1,3},  {2,1}{2,2}{2,3},  {3,1}{3,2}{3,3},  }

A X A = {1,1}{1,2}{1,3},  {2,1}{2,2}{2,3},  {3,1}{3,2}{3,3},  }

1.6             Partition of set: A collection of subsects of A is called a parition or quaotient set of a non – empty set A.

Q.) Let A = { 1, 2,3,4,5,6}. Find whether or not each of following is a portion of A

P = [{1,3,5}, {2, 4 ,5,6}]

P= [{1,2}, {3,4,5}{6}]

* Relation : It’s a relation between two object.

* Diagram of Relation : A {1,2,3,4} B = {a,b}

1.7 Matrix of Relation :- If A = {a1, a2  am}

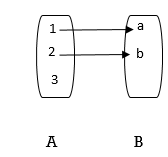
B= {b1, b2, bn} are finite sets containing m and n elements resp & of R is a relation from A to B we represent R by matrix MR = [mij]

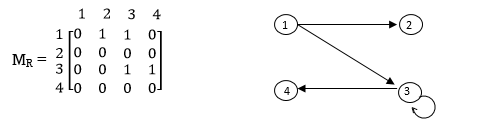
Q) Let the matrix of a relation between

A = [ 1, 2, 3}    B = {a, b, c, d, } be

MR= 

Write the relation ,

 R= {(1, 1), (1,d), (2, b), (2, d), (3, a), (3,c) }

* Digraph of a Relation:-

1) Let A = { 1, 2, 3, 4 } and let R be the relation greater than. Represent R as a set a diagraph, matrix and diagram.

 R= { (2, 1), (3,1), (4,1), (3,2), (4,2) (4,3) }

1.8 Types of Relation

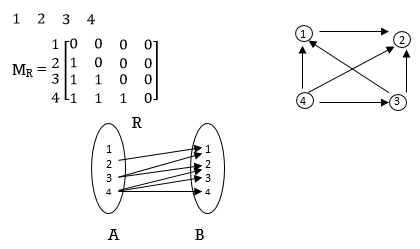
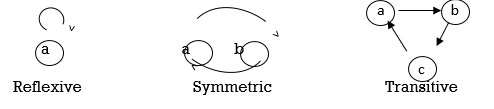
1) Reflexive :- A relation R on set A is called reflexive  if a related to a itself ie. ( a r a) R for all a A ie if a R a for all a A  

2) Irreflexive  :-

Some elements have zero is non-zero elements in diagonal.

* Symmetric :- A relation R on set A is called symmetric if whenever aRb have bRa.

* Asymmetric :-A relation R on A is called asymmetric if whenever aRb then

bRa.

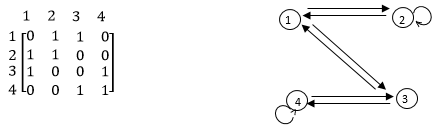
Q) Let A= { 1, 2, 3, 4} & R = { (1, 2) (2,1) (2,2), (3,1) (1,3) (4,3), (4,4)}

 The relation is symmetric because whenever aRb we have bRa. Its matrix & diagraph are

Q) Let A = {1, 2, 3, 4} and R= {(1, 2), (1,3) , (3,3), (3,4)} state the nature of relation. Give its matrix is diagraph.

 The relation is not symmetric because (1,2)  R but (2,1) R.

The relation is not asymmetric because (3, 3) R.

The relation is anti symmetric because whenever aRb, bRa a=b. e.g. (3,3) R and whenever a b then either aRb or b Ra

* Note :- No. Of symmetric relation that can be defined a set A with n elements is 2n(n+1)/2

* Note :- The no. Of reflexive  & symmetric relation that can be defined on set A is 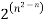/2

* Transitive elements: - A relation R on set A is called Transitive of whenever aRb and bRC then a Rc.

* Relation of path of length n :- Let R be relation defined on a set A. A finite sequence    :1, x1 , x2….xn1, be such that Rx, x1 Rx2, …..xn1is called a path of length n from a to b.

a R2b   there is path from a to b of length

a R3 c   there is path of length 3.

* In a path of length n; elements are (n +1)

1) Let A ={ a, b, c, d, e} and R ={ (a, a) (a,b) (b,a) (b,c) (a,d) (d,c), (d,e)}find R

 aR1a    since   aRa

 aR1b    since   aRb

AR1d    since   aRd

AR2c    since   aRb,  bRc

 aR2e      aRd,  bRe

 aR1a      aRa

AR1c      aRc

AR2d     aRa,   aRd

AR3e     aRa,   aRb

DR1c    bRa, aRd,    dRe

DR1e    bRc

BR2b    dRe

R= { (a, a) (a,b) (a,c) (a,d) (a,e) (b,b), (b,a) (b,c) (b,d) (b,e,) (d,c, (d,e)}

Equivalence :- If  a is an element of A and R is an equivalence relation then the set of x A such that aRx is called equivalence class of a induced by partion denoted by R(a) E(a) or [a]

1) Let A = { 1, 2, 3, 4, 5} find the equivalence  relation in A which generates the partition {(1, 3, 5), (2, 4) }.

 

2R2, 4R4, 2R4, 4R2

R= { (1,1), (1,3), (3,1), (1,5), (5,1) (3,3), (3,5), (5,3),

(5,5), (2,2), (2,4), (4,2) (4,4)}

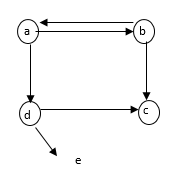
Q) Let A = { a, b, c, d, e } and let R and S be two Relation on A whose diagraph are shown :-

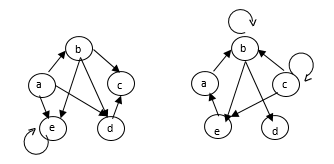
Find R, R1, R⋂S & R⋃S.

 Step 1:- Find A x A

{ (a,a) (a,b) (a,c) (a,d) (a,e 

(b,a) (b,b) (b,c) (b,d) (b,e,) 

(c,a) (c,b) (c,c) (c,d), (c,e,)

(d, a) (d,b) (d,c) (d,d) (d,e,)

(e,a) (e,b) (e,c) (e,d) (e,e) }

By diagraph.

R= { (a, b) (a,d) (a,e) (b,c) (b,d) (b,e) (c,c,) (d,d) (e,e)

S = { a, a) (a, b) (b,b) (b,e,) (c,c) (c,b) (c,e,) (d,b) (e,a,) (e,d)}

R= { elements of A XA which are not in R}

= { (a,a) (a,c), (b,a) (b,b) (c,a) (c,b) (c,d) (c,e,) (d,a) (d,b) (d,c) (d,e) (e,a) (e,b) (e,c) (e,d)}

R1 = {elements in R with reverse order }

= {(b,a,) (d,a) (e,a) (c,b) (d,b) (e,b) (c,c,) (d,d) (e,e)}

R⋂S = { elements common to both R & S}

{ (b,e, (c,c) }

R⋃S = { elements in R & S}

{ (a, a) (a,b) (a,d) (a,e) (b,b) (b,c) (b,d) (b,e) (c,c) (c,e,) (d,b)

(d,d) (e,a) (e,d) (e,e)}

1.9 Functions:-

Domain :- The set of elements of A is called domain

* Range :- The set of elements or images or value is called range of function B is called co-main

1.10 Characteristic function of sets:

Surjective :- “On to”

Every element of co-domain there exist at least one element such that f(x)=y

Every element of y must be mapped by x.

* Injective :- “One-to-one”

* For any y  y  there is at most x such that f of  x is equal to y.

* Every x is mapped to y.

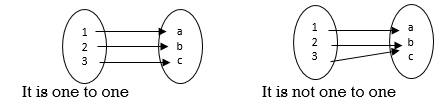
 Injective      Not an injective

* Bijective :-  If both one to one & onto them f is called bijective.

1.11 Types of functions.

1. Constant function: - Let f  be a function define from set A to Set B where B has only  one  element and all element of set B  linked with single element of set B.
2. Equality of function:- If f : x   y and g : x  y are function then f = g if and only if f(x) = g (x) for all 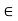x X.

Example: Let x = {0, 1, 2} and let function f and g are defined from x to X as for all x in X.

f(x) = (x2 + x + 1) mod 3 and

g(x) = (x + 2)2 mod 3

Does f = g?

Here + f(x) = g(x)

Both f and g are equal function:-

3.     Logarithmic Function:- Let b be a positive real number & b ≠ 1. The logarithmic function with box b is the function from R+ to R that take each positive real number x to logb x.

Example:  a) log2 8 = 3   b) log22m = 3

c) log10 1 = 0    d) log21 4 = 1

4.     Hamming Function:- Richard  W – Hamming defined the function which measures the difference between two strings of o’s & 1’s that home some length.

e.g. Let function H:- S X s  z

Where (s, t) 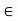s x S

H(11010,a0001) give result 3 as the position of 1st string differ at 3 places from 2nd string.

a)     H(11010,10001) = 3

b)    H (100000, 111111) = 5

5.     Identify Funciton : Let x be the set & I : x  X be function such that.

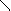I (x) = x for all z 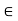L

Then function I is called Identity

6.     Inverse Function:- If f is a function defined from set A to set B is one – one and onto then there exist a function.

F-1 (y) = x  F(x) = y

7.     Composite Function: Composition of function is when one function inside another function. The rotation used for the composition of function is fog (x)

Means fog (x) = f {g(x)}

1.12 Composition of function:-

Consider the following two function f(x)= x2 and g(x) = 2x + 1

We can construct another function h(x)=2x2+1 form f and g

While constructing h, we use two rules successively,

x x2& then x22(n2) + 1

The first is obtained by rule f to x & second is obtained by rule g to f(x) = x2.

Thus h (x) = g[(x)] = g(x2)

= 2(x2) + 1

= 2 x2 + 1

H is called composition of g and f

We have composition of f and g.

H(x) = f [g(x)]

= f(2x+1)

= (2x + 1)2

G [f(x)] is denoted by gof:

F [g(x)] is denoted by fog:

Q) Let A = B =C= R & Let f  A B &

g: B C be & defined by f(a) = a-1

g(b) = b2. Find   i) fog (2)       ii) (gof) (x2)

 i) fog = f [g(x) ] = f (x2) = x21

Fog (2) =  221 = 3

Ii) gof = g [f (x)] = g (x1) =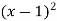

        Inverse function: Let f : x – y suppose g is a function g : x – y such that (gof) = x 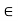 X and (fog) y = Y for every y 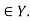Then g is called inverse of f &  denoted by f-1

Q. Consider the function f and g given by following relation.

f : {(1, -1), (2, -2), (3, -3), (4, - 4)}

g : {(-1, 1), (-2, 2), (-3, 3), (-4, 4)}

Show that g = f-1

Solution : (gof) (1) = g{f(1)}

= g (-1) = 1

(fog) (-1) = f {g(-1)}= f(1) = -1

And this is true for every 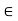y Y

Hence g = f

1.13 Countable:-

Finite sets are countable sets

The integers Z from a countable set, a bijection from Z to N is given by

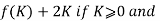
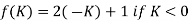
So f maps 0.1.2.3…to 0,2,4,6… and f maps -1,-2,-3,-4,… to 1,3,5,7…

1.14 Uncountable

A set is said to be uncountable if it is not countable. If we have an infinite countable set, it automatically is equivalent to N.

1.15 Cantor diagonal method

It is the method used to show that the integers and real cannot be e put into one to one correspondence.

Given any set S, consider the power set, 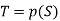consisting all subset of S.

Cantor diagonal method is used to show that T is larger than S i.e. there exist an injection but no bijection from S to T.

Finding an injection is trivial, the function from S to T which maps and element s of S to the singleton set (S).

Suppose there exist a bijection 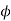from S to T and consider that subset D of S consisting of the element d of S such that 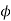(d) does not contain d.

Since 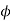is a bijection, there must exist an element x of S such that 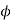(x) = D.

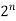Cantor diagonal method applies to any set s, finite or infinite. If S is a finite set of cardinality n, then has cardinality which is larger than n.

If S is an infinite set, then 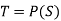is a bigger finite set.

In particular, the cardinality c of the real number R, which can be shown to be isomorphic to P(N).

1.16 Cantor Power set Theorem: Uncountable set

Cantor's power set theorem says that if S is any set, then there is an injection from S to P(S) but no bijection.

So,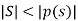

The first part of the theorem

For any set S, the map p: S → p(S) – {S} define for any S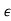 S, gives a well-defined injection from S →P(s)

Second part

Let q : S → p(S) be a map

Put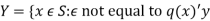

Then Y is well defined subset of S. We prove that no 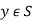exists, such that q(y) = Y for some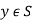

Suppose the contrary so there is 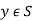with q(y) = Y.

We ask, if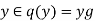

If 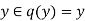then 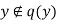is false, so by definition of Y we have 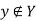,a contradiction.

So both condition 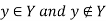lead to contradiction. So the assumption that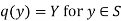

So no such y exists.

So the set Y is not in range of q. So q is not surjective.

We have proved that for any set S, there is no surjection from S → P(s), so no bijection either.

1.17 The Schroeder Bernstein theorem

If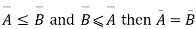

Proof:- We may assume that A and B are disjoint and, suppose f A → B and g :A→B are both injections, we need to find a bijection h : A →B.

Observe that if a is in A there is at most one 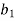in B such that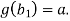

At most one 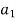in A such that 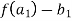. Continuing in this way we can find string of ancestor of a.

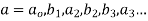
Search that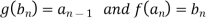

Call this the linage of a.

Any 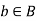also has linage.

The linage may take three forms, it may be infinite, it may end at some term 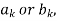if 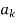is not in the image of g or 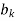is not in the image of f

1.18 Propositional logic

Definition :-

A proposition is a statement that is that true or false.

Example:- 1) Mumbai is located in India…(T)

2) 5+2=8  (F)

3) It is sunny day… (either T or F)

Example:- 1) How are you?

A question is not a proposition.

2) x + 5 = 8

Since x is not specified, neither true nor false.

Propositional logic Syntax:-

Sentences is proportional logic

Atomic sentences

1)     Constructed from constant and propositional logic symbols.

2)     True, false are atomic sentences.

1.19  Composite sentences

Constructed from valid sentences via connectives.

If A,B are sentences then

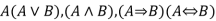
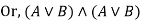
Propositional logic semantics

It is giving meaning two sentences.

The semantic in the propositional logic is defined by

1)     Interpretation of propositional symbols and constants.

2)     Through the meaning of connectives.

Semantics : Propositional symbols

A propositional symbol is a statement that is either true or false.

True (T) or False (F).

I : The girl is dancing – True

I' : The girl is not dancing. – False

1.20 Power sets:

It  is a given set then the set of all subset of s is called power set of s and is denoted by p(s)

Eg:- If s = {a, b} then P(s) = H {ø(a), (b), (a, b)}

Q. If A = {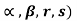 find power set of A.

P(A) = [ø((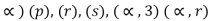

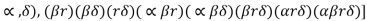
              Ordered set: A set as we know is a collection of object will no reference to the order in which the element of the set are written.

If use assign a position to each element of a set then the set is called an ordered set.

              N – tupple: An ordered set with n elements is called n – tupple.

              Two n – tupple are equal if and only if their corresponding elements are equal. The ordered (a1, a2………..an) and (b1, b2………..bn) are equal if &  only if a1= b1 for every i .