1.1 CPU memory inputoutput subsystems the control unit

COA

UNIT - 1

Functional blocks of a computer, Data representation

1.1 CPU, memory, input-output subsystems, the control unit

A Central Processing Unit is also called a processor, central processor, or microprocessor. It carries out all the important functions of a computer. It receives instructions from both the hardware and active software and produces output accordingly. It stores all important programs like operating systems and application software. CPU also helps Input and output devices to communicate with each other. Owing to these features of the CPU, it is often referred to as the brain of the computer.

CPU is installed or inserted into a CPU socket located on the motherboard. Furthermore, it is provided with a heat sink to absorb and dissipate heat to keep the CPU cool and functioning smoothly.

Generally, a CPU has three components:

ALU (Arithmetic Logic Unit)

Control Unit

Memory or Storage Unit

CPU

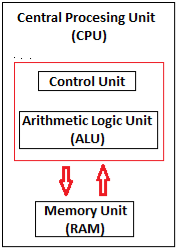
Fig 1 - CPU

Control Unit: It is the circuitry in the control unit, which makes use of electrical signals to instruct the computer system for executing already stored instructions. It takes instructions from memory and then decodes and executes these instructions. So, it controls and coordinates the functioning of all parts of the computer. The Control Unit's main task is to maintain and regulate the flow of information across the processor. It does not take part in processing and storing data.

ALU: It is the arithmetic logic unit, which performs arithmetic and logical functions. Arithmetic functions include addition, subtraction, multiplication division, and comparisons. Logical functions mainly include selecting, comparing, and merging the data. A CPU may contain more than one ALU. Furthermore, ALUs can be used for maintaining timers that help run the computer.

Memory or Storage Unit/ Registers: It is called Random access memory (RAM). It temporarily stores data, programs, and intermediate and final results of processing. So, it acts as a temporary storage area that holds the data temporarily, which is used to run the computer.

What is CPU Clock Speed?

The clock speed of a CPU or a processor refers to the number of instructions it can process in a second. It is measured in gigahertz. For example, a CPU with a clock speed of 4. 0 GHz means it can process 4 billion instructions in a second.

Types of CPU:

CPUs are mostly manufactured by Intel and AMD, each of which manufactures its types of CPUs. In modern times, there are lots of CPU types in the market. Some of the basic types of CPUs are described below:

Single Core CPU: Single Core is the oldest type of computer CPU, which was used in the 1970s. It has only one core to process different operations. It can start only one operation at a time; the CPU switches back and forth between different sets of data streams when more than one program runs. So, it is not suitable for multitasking as the performance will be reduced if more than one application runs. The performance of these CPUs is mainly dependent on the clock speed. It is still used in various devices, such as smartphones.

Dual-Core CPU: As the name suggests, Dual Core CPU contains two cores in a single Integrated Circuit (IC). Although each core has its controller and cache, they are linked together to work as a single unit and thus can perform faster than the single-core processors and can handle multitasking more efficiently than Single Core processors.

Quad-Core CPU: This type of CPU comes with two dual-core processors in one integrated circuit (IC) or chip. So, a quad-core processor is a chip that contains four independent units called cores. These cores read and execute instructions of the CPU. The cores can run multiple instructions simultaneously, thereby increases the overall speed for programs that are compatible with parallel processing.

Quad-Core CPU uses a technology that allows four independent processing units (cores) to run in parallel on a single chip. Thus by integrating multiple cores in a single CPU, higher performance can be generated without boosting the clock speed. However, the performance increases only when the computer's software supports multiprocessing. The software which supports multiprocessing divides the processing load between multiple processors instead of using one processor at a time.

History of CPU:

Some of the important events in the development of CPU since its invention till date are as follows:

In 1823, Baron Jons Jackob Berzelius discovered silicon that is the main component of the CPU to date.

In 1903, Nikola Tesla got gates or switches patented, which are electrical logic circuits.

In December 1947, John Bardeen, William Shockley, and Walter Brattain invented the first transistor at the Bell Laboratories and got it patented in 1948.

In 1958, the first working integrated circuit was developed by Robert Noyce and Jack Kilby.

In 1960, IBM established the first mass-production facility for transistors in New York.

In 1968, Robert Noyce and Gordon Moore founded Intel Corporation.

AMD (Advanced Micro Devices) was founded in May 1969.

In 1971, Intel introduced the first microprocessor, the Intel 4004, with the help of Ted Hoff.

In 1972, Intel introduced the 8008 processor; in 1976, Intel 8086 was introduced, and in June 1979, Intel 8088 was released.

In 1979, a 16/32-bit processor, the Motorola 68000, was released. Later, it was used as a processor for the Apple Macintosh and Amiga computers.

In 1987, Sun introduced the SPARC processor.

In March 1991, AMD introduced the AM386 microprocessor family.

In March 1993, Intel released the Pentium processor. In 1995, Cyrix introduced the Cx5x86 processor to give competition to Intel Pentium processors.

In January 1999, Intel introduced the Celeron 366 MHz and 400 MHz processors.

In April 2005, AMD introduced its first dual-core processor.

In 2006, Intel introduced the Core 2 Duo processor.

In 2007, Intel introduced different types of Core 2 Quad processors.

In April 2008, Intel introduced the first series of Intel Atom processors, the Z5xx series. They were single-core processors with a 200 MHz GPU.

In September 2009, Intel released the first Core i5 desktop processor with four cores.

In January 2010, Intel released many processors such as Core 2 Quad processor Q9500, first Core i3 and i5 mobile processors, first Core i3 and i5 desktop processors. In the same year in July, it released the first Core i7 desktop processor with six cores.

In June 2017, Intel introduced the first Core i9 desktop processor.

In April 2018, Intel released the first Core i9 mobile processor.

Computer Memory

The computer memory holds the data and instructions needed to process raw data and produce output. The computer memory is divided into a large number of small parts known as cells. Each cell has a unique address which varies from 0 to memory size minus one.

Computer memory is of two types: Volatile (RAM) and Non-volatile (ROM). The secondary memory (hard disk) is referred to as storage, not memory.

But, if we categorize memory on behalf of space or location, it is of four types:

Cache memory

Primary memory

Secondary memory

Register memory is the smallest and fastest memory in a computer. It is not a part of the main memory and is located in the CPU in the form of registers, which are the smallest data holding elements. A register temporarily holds frequently used data, instructions, and memory addresses that are to be used by the CPU. They hold instructions that are currently processed by the CPU. All data is required to pass through registers before it can be processed. So, they are used by the CPU to process the data entered by the users.

Registers hold a small amount of data around 32 bits to 64 bits. The speed of a CPU depends on the number and size (no. of bits) of registers that are built into the CPU. Registers can be of different types based on their uses. Some of the widely used Registers include Accumulator or AC, Data Register or DR, the Address Register or AR, Program Counter (PC), I/O Address Register, and more.

Types and Functions of Computer Registers:

Data Register: It is a 16-bit register, which is used to store operands (variables) to be operated by the processor. It temporarily stores data, which is being transmitted to or received from a peripheral device.

Program Counter (PC): It holds the address of the memory location of the next instruction, which is to be fetched after the current instruction is completed. So, it is used to maintain the path of execution of the different programs and thus executes the programs one by one, when the previous instruction gets completed.

Instructor Register: It is a 16-bit register. It stores the instruction which is fetched from the main memory. So, it is used to hold instruction codes, which are to be executed. The Control Unit takes instruction from the Instructor Register, then decodes and executes it.

Accumulator Register: It is a 16-bit register, which is used to store the results produced by the system. For example, the results generated by the CPU after the processing are stored in the AC register.

Address Register: It is a 12-bit register that stores the address of a memory location where instructions or data is stored in the memory.

I/O Address Register: Its job is to specify the address of a particular I/O device.

I/O Buffer Register: Its job is to exchange the data between an I/O module and the CPU.

Cache Memory

Cache memory is a high-speed memory, which is small in size but faster than the main memory (RAM). The CPU can access it more quickly than the primary memory. So, it is used to synchronize with a high-speed CPU and to improve its performance.

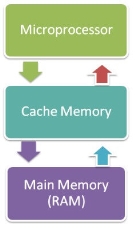
Cache Memory

Fig 2 - Memory

Cache memory can only be accessed by the CPU. It can be a reserved part of the main memory or a storage device outside the CPU. It holds the data and programs which are frequently used by the CPU. So, it makes sure that the data is instantly available for the CPU whenever the CPU needs this data. In other words, if the CPU finds the required data or instructions in the cache memory, it doesn't need to access the primary memory (RAM). Thus, by acting as a buffer between RAM and CPU, it speeds up the system performance.

Types of Cache Memory:

L1: It is the first level of cache memory, which is called Level 1 cache or L1 cache. In this type of cache memory, a small amount of memory is present inside the CPU itself. If a CPU has four cores (quad-core CPU), then each core will have its level 1 cache. As this memory is present in the CPU, it can work at the same speed as the CPU. The size of this memory ranges from 2KB to 64 KB. The L1 cache further has two types of caches: The instruction cache, which stores instructions required by the CPU, and the data cache that stores the data required by the CPU.

L2: This cache is known as Level 2 cache or L2 cache. This level 2 cache may be inside the CPU or outside the CPU. All the cores of a CPU can have their separate level 2 cache, or they can share one L2 cache among themselves. In case it is outside the CPU, it is connected with the CPU with a very high-speed bus. The memory size of this cache is in the range of 256 KB to 512 KB. In terms of speed, they are slower than the L1 cache.

L3: It is known as Level 3 cache or L3 cache. This cache is not present in all the processors; some high-end processors may have this type of cache. This cache is used to enhance the performance of Level 1 and Level 2 cache. It is located outside the CPU and is shared by all the cores of a CPU. Its memory size ranges from 1 MB to 8 MB. Although it is slower than L1 and L2 cache, it is faster than Random Access Memory (RAM).

How does cache memory work with CPU?

When the CPU needs the data, first of all, it looks inside the L1 cache. If it does not find anything in L1, it looks inside the L2 cache. If again, it does not find the data in the L2 cache, it looks into the L3 cache. If data is found in the cache memory, then it is known as a cache hit. On the contrary, if data is not found inside the cache, it is called a cache miss.

If data is not available in any of the cache memories, it looks inside the Random Access Memory (RAM). If RAM also does not have the data, then it will get that data from the Hard Disk Drive.

So, when a computer is started for the first time, or an application is opened for the first time, data is not available in cache memory or RAM. In this case, the CPU gets the data directly from the hard disk drive. Thereafter, when you start your computer or open an application, the CPU can get that data from cache memory or RAM.

Primary Memory

Primary Memory is of two types: RAM and ROM.

RAM (Volatile Memory)

It is a volatile memory. It means it does not store data or instructions permanently. When you switch on the computer the data and instructions from the hard disk are stored in RAM.

CPU utilizes this data to perform the required tasks. As soon as you shut down the computer the RAM loses all the data.

ROM (Non-volatile Memory)

It is a non-volatile memory. It means it does not lose its data or programs that are written on it at the time of manufacture. So it is a permanent memory that contains all important data and instructions needed to perform important tasks like the boot process.

Secondary Memory

The secondary storage devices which are built into the computer or connected to the computer are known as a secondary memory of the computer. It is also known as external memory or auxiliary storage.

The secondary memory is accessed indirectly via input/output operations. It is non-volatile, so permanently stores the data even when the computer is turned off or until this data is overwritten or deleted. The CPU can't directly access the secondary memory. First, the secondary memory data is transferred to primary memory then the CPU can access it.

Some of the secondary memory or storage devices are described below:

1) Hard Disk:

It is a rigid magnetic disc that is used to store data. It permanently stores data and is located within a drive unit.

Secondary Memory

Fig 3 – Hard disk

The hard disk is also known as a hard drive. It is a rigid magnetic disc that stores data permanently, as it is a non-volatile storage device. The hard disk is located within a drive unit on the computer's motherboard and comprises one or more platters packed in an air-sealed casing. The data is written on the platters by moving a magnetic head over the platters as they spin. The data stored on a computer's hard drive generally includes the operating system, installed software, and the user's files and programs, including pictures, music, videos, text documents, etc.

Components of Hard Drive:

The main components of a hard drive include a head actuator, read/write actuator arm, read/write head, platter, and spindle. A circuit board, which is called the disk controller or interface board, is present on the back of a hard drive. It allows the hard drive to communicate with the computer.

2) Solid-state Drive:

Secondary Memory

Fig 4 - SSD

SSD (Solid State Drive) is also a non-volatile storage medium that is used to hold and access data. Unlike a hard drive, it does not have moving components, so it offers many advantages over SSD, such as faster access time, noiseless operation, less power consumption, and more.

As the cost of SSD has come down, it has become an ideal replacement for a standard hard drive in desktop and laptop computers. It is also suitable for notebooks, and tablets that don't require lots of storage.

3) Pen drive:

Secondary Memory

Fig 5 – Pen drive

Pen drive is a compact secondary storage device. It is also known as a USB flash drive, thumb drive, or jump drive. It connects to a computer via a USB port. It is commonly used to store and transfer data between computers. For example, you can write a report using a computer and then copy or transfer it to the pen drive. Later, you can connect this pen drive to a computer to see or edit your report. You can also store your important documents and pictures, music, videos in the pen drive and keep them in a safe place.

Pen drive does not have movable parts; it comprises an integrated circuit memory chip that stores the data. This chip is housed inside a plastic or aluminium casing. The data storage capacity of the pen drive generally ranges from 2 GB to 128 GB. Furthermore, it is a plug and play device as you don't need additional drives, software, or hardware to use it.

4) SD Card:

Secondary Memory

Fig 6 – SD card

SD Card stands for Secure Digital Card. It is most often used in portable and mobile devices such as smartphones and digital cameras. You can remove it from your device and see the things stored in it using a computer with a card reader.

There are many memory chips inside the SD card that store the data; it does not have moving parts. SD cards are not created equal, so they may differ from each other in terms of speed, physical sizes, and capacity. For example, standard SD cards, mini SD cards, and micro SD cards.

5) Compact Disk (CD):

Secondary Memory

Fig 7 - CD

Compact Disk is a portable secondary storage device in the shape of a round medium disk. It is made of polycarbonate plastic. The concept of CD was co-developed by Philips and Sony in 1982. The first CD was created on 17 August 1982 at the workshop of Philips in Germany.

In the beginning, it was used for storing and playing sound recordings, later it was used for various purposes such as for storing documents, audio files, videos, and other data like software programs in a CD.

Physical characteristics of a CD/ Structure of CD:

A standard CD is around 5 inches in diameter and 0. 05 inches in thickness. It is made of a clear polycarbonate plastic substrate, a reflective metallic layer, and a clear coating of acrylic plastic. These thin circular layers are attached one on top of another as described below:

A polycarbonate disc layer at the bottom has the data encoded by creating lands and pits.

The polycarbonate disc layer is coated with a thin aluminium layer that reflects the laser.

The reflective aluminium layer is coated with a lacquer layer to prevent oxidation to protect the below layers. It is generally spin coated directly on the top of the reflective layer.

The label print is applied on the lacquer layer, or artwork is screen printed on the top of the disc on the lacquer layer by offset printing or screen printing.

How Does a CD Work?

The data or information is stored or recorded or encoded in CD digitally using a laser beam that etches tiny indentations or bumps on its surface. The bump is called a pit, which represents the number 0. Space, where the bump is not created, is called land, and it represents the number 1. Thus, the data is encoded into a compact disc by creating pits (0) and lands (1). The CD players use laser technology to read the optically recorded data.

6) DVD:

Secondary Memory

Fig 8 - DVD

DVD is short for digital versatile disc or digital video disc. It is a type of optical media used for storing optical data. Although it has the same size as a CD, its storage capacity is much more than a CD. So, it is widely used for storing and viewing movies and to distribute software programs as they are too large to fit on a CD. DVD was co-developed by Sony, Panasonic, Philips, and Toshiba in 1995.

Types of DVDs:

DVDs can be divided into three main categories which are as follows:

DVD-ROM (Read-Only): These types of DVDs come with media already recorded on them, such as movie DVDs. As the name suggests, data on these discs cannot be erased or added, so these discs are known as a read-only or non-writable DVD.

DVD-R (Writable): It allows you to record or write information to the DVD. However, you can write information only once as it becomes a read-only DVD once it is full.

DVD-RW (Rewritable or Erasable): This type of discs can be erased, written, or recorded multiple times.

I/O Systems and Subsystems

I/O devices are very important in computer systems. They provide users the means of interacting with the system. So there is a separate I/O system devoted to handling the I/O devices.

The different Components of the I/O systems are −

I/O Hardware

There are many I/O devices handled by the operating system such as a mouse, keyboard, disk drive, etc. Different device drivers can be connected to the operating system to handle a specific device. The device controller is an interface between the device and the device driver.

A diagram to represent this is −

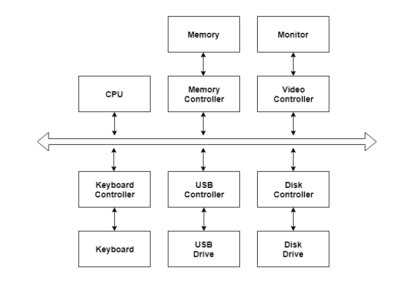
Fig 9 – I/O Hardware

I/O Application Interface

The user applications can access all the I/O devices using the device drivers, which are device-specific codes. The application layer sees a common interface for all the devices.

This is illustrated using the below image −

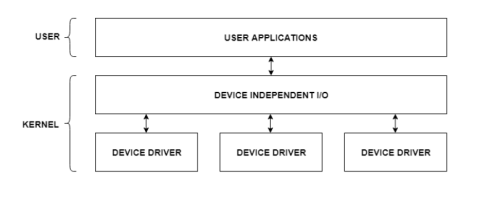
Fig 10 – I/O Application Interface

Most of the devices are either block I/O and character I/O devices. Block devices are accessed one block at a time whereas character devices are accessed one character at a time.

I/O Software

The I/O software contains the user-level libraries and the kernel modules. The libraries provide the interface to the user program to perform input and output. The kernel modules provide the device drivers that interact with the device controllers.

The I/O software should be device-independent so that the programs can be used for any I/O device without specifying it in advance. For example - A program that reads a file should be able the read the file on a hard disk, floppy disk, CD-ROM, etc. without having to change the program each time.

Control unit

During the execution of a program, the control unit fetches one instruction at a time from the main memory and then executes it. In this execution process, it takes the help of ALU, if the instruction execution involves arithmetic or logical operation (like AND, OR, Ex-OR). After the execution of the current instruction, the CPU fetches the next instruction for execution. This process continues until the program is completed and the result is output using the output device. In many computers, the control unit and the ALU are integrated into a single block, known as Central Processing Unit (CPU).

Central Processing Unit (CPU) consists of the following features −

CPU is considered as the brain of the computer.

CPU performs all types of data processing operations.

It stores data, intermediate results, and instructions (program).

It controls the operation of all parts of the computer.

Fig 11 - Processor

CPU itself has the following three components.

Memory or Storage Unit

a control unit

ALU(Arithmetic Logic Unit)

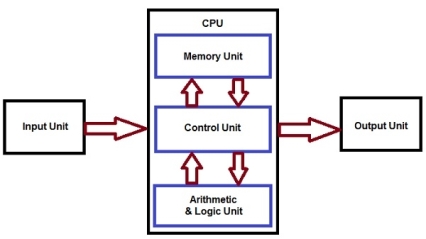
Fig 12 – Control Unit

Memory or Storage Unit

This unit can store instructions, data, and intermediate results. This unit supplies information to other units of the computer when needed. It is also known as an internal storage unit or the main memory or the primary storage or Random Access Memory (RAM).

Its size affects speed, power, and capability. Primary memory and secondary memory are two types of memories in the computer. Functions of the memory unit are −

It stores all the data and the instructions required for processing.

It stores intermediate results of processing.

It stores the final results of processing before these results are released to an output device.

All inputs and outputs are transmitted through the main memory.

Control unit

This unit controls the operations of all parts of the computer but does not carry out any actual data processing operations.

Functions of this unit are −

It is responsible for controlling the transfer of data and instructions among other units of a computer.

It manages and coordinates all the units of the computer.

It obtains the instructions from the memory, interprets them, and directs the operation of the computer.

It communicates with input/output devices for the transfer of data or results from storage.

It does not process or store data.

ALU (Arithmetic Logic Unit)

This unit consists of two subsections namely,

Arithmetic section

Logic Section

Arithmetic section

The function of the arithmetic section is to perform arithmetic operations like addition, subtraction, multiplication, and division. All complex operations are done by making repetitive use of the above operations.

Logic Section

The function of the logic section is to perform logic operations such as comparing, selecting, matching, and merging data.

Key takeaway

1.2 Instruction set architecture of CPU–registers

This means that an ISA describes the design of a Computer in terms of the basic operations it must support. The ISA is not concerned with the implementation-specific details of a computer. It is only concerned with the set or collection of basic operations the computer must support. For example, the AMD Athlon and the Core 2 Duo processors have entirely different implementations but they support more or less the same set of basic operations as defined in the x86 Instruction Set.

Let us try to understand the Objectives of an ISA by taking the example of the MIPS ISA. MIPS is one of the most widely used ISAs in education due to its simplicity.

The ISA defines the types of instructions to be supported by the processor.
Based on the type of operations they perform MIPS Instructions are classified into 3 types:

Arithmetic/Logic Instructions:

These Instructions perform various Arithmetic & Logical operations on one or more operands.

Data Transfer Instructions:

These instructions are responsible for the transfer of instructions from memory to the processor registers and vice versa.

Branch and Jump Instructions:

These instructions are responsible for breaking the sequential flow of instructions and jumping to instructions at various other locations, this is necessary for the implementation of functions and conditional statements.

2. The ISA defines the maximum length of each type of instruction.

Since the MIPS is a 32 bit ISA, each instruction must be accommodated within 32 bits.

3. The ISA defines the Instruction Format of each type of instruction. The Instruction Format determines how the entire instruction is encoded within 32 bits

There are 3 types of Instruction Formats in the MIPS ISA:

R-Instruction Format

I-Instruction Format

J-Instruction Format

Each of the above Instruction Formats has different instruction encoding schemes, and hence need to be interpreted differently by the processor.

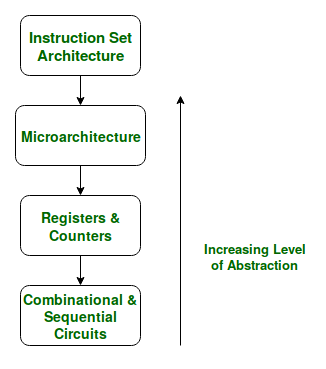
If we look at the Abstraction Hierarchy:

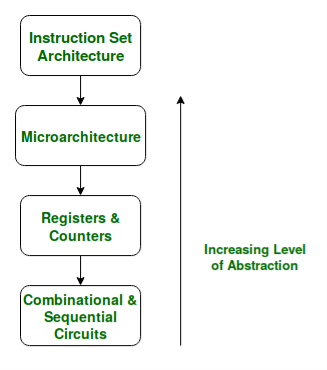
Fig 13 – The Abstraction Hierarchy

We note that the Microarchitectural level lies just below the ISA level and hence is concerned with the implementation of the basic operations to be supported by the Computer as defined by the ISA. Therefore we can say that the AMD Athlon and Core 2 Duo processors are based on the same ISA but have different microarchitectures with different performance and efficiencies.

Now one may ask the need to distinguish between Microarchitecture and ISA?

The answer to this lies in the need to standardize and maintain the compatibility of programs across different hardware implementations based on the same ISA. Making different machines compatible with the same set of basic instructions (The ISA) allows the same program to run smoothly on many different machines thereby making it easier for the programmers to document and maintain code for many different machines simultaneously and efficiently.

This Flexibility is the reason we first define an ISA and then design different microarchitectures complying with this ISA for implementing the machine. The design of an ISA is one of the major tasks in the study of Computer Architecture.

Instruction Set Architecture	Microarchitecture
The ISA is responsible for defining the set of instructions to be supported by the processor. For example, some of the instructions defined by the ARMv7 ISA are given below.	The Microarchitecture is more concerned with the lower-level implementation of how the instructions are going to be executed and deals with concepts like Instruction Pipelining, Branch Prediction, Out of Order Execution.
The Branch of Computer Architecture is more inclined towards the Analysis and Design of Instruction Set Architecture. For Example, Intel developed the x86 architecture, ARM developed the ARM architecture, & AMD developed the amd64 architecture. The RISC-V ISA developed by UC Berkeley is an example of an Open Source ISA.	On the other hand, the Branch of Computer Organization is concerned with the implementation of a particular ISA deals with various hardware implementation techniques, i. e. is the Microarchitecture level. For Example, ARM licenses other companies like Qualcomm, Apple for using it ARM ISA, but each of these companies have their implementations of this ISA thereby making them different in performance and power efficiency. The Krait cores developed by Qualcomm have a different microarchitecture and the Apple A-series processors have a different microarchitecture.

The x86 was developed by Intel, but we see that almost every year Intel comes up with a new generation of i-series processors. The x86 architecture on which most of the Intel Processors are based essentially remains the same across all these generations but, where they differ is in the underlying Microarchitecture. They differ in their implementation and hence are claimed to have improved Performance. These various Microarchitectures developed by Intel are codenamed as ‘Nehalem’, ‘Sandybridge’, ‘Ivybridge’, and so on.

Therefore, in conclusion, we can say that different machines may be based on the same ISA but have different Microarchitectures.

Key takeaway

1.3 Instruction execution cycle

A program residing in the memory unit of a computer consists of a sequence of instructions. These instructions are executed by the processor by going through a cycle for each instruction.

In a basic computer, each instruction cycle consists of the following phases:

Fetch the instruction from memory.

Decode the instruction.

Read the effective address from memory.

Execute the instruction.

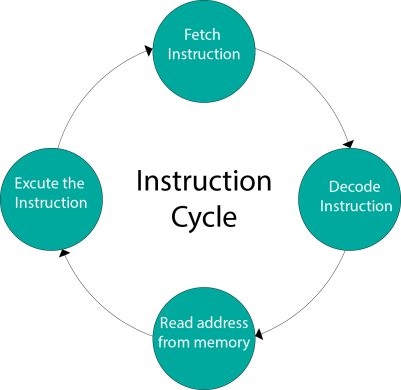
Instruction Cycle

Fig 14 - Input-Output Configuration

In computer architecture, input-output devices act as an interface between the machine and the user.

Instructions and data stored in the memory must come from some input device. The results are displayed to the user through some output device.

The following block diagram shows the input-output configuration for a basic computer.

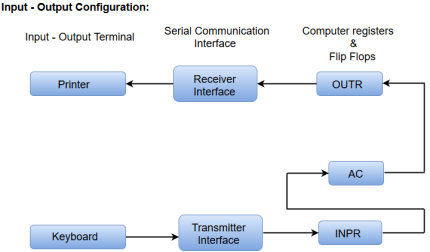
Instruction Cycle

Fig 15 – I/O configuration

The input-output terminals send and receive information.

The amount of information transferred will always have eight bits of an alphanumeric code.

The information generated through the keyboard is shifted into an input register 'INPR'.

The information for the printer is stored in the output register 'OUTR'.

Registers INPR and OUTR communicate with a communication interface serially and with the AC in parallel.

The transmitter interface receives information from the keyboard and transmits it to INPR.

The receiver interface receives information from OUTR and sends it to the printer serially.

Design of a Basic Computer

A basic computer consists of the following hardware components.

A memory unit with 4096 words of 16 bits each

Registers: AC (Accumulator), DR (Data register), AR (Address register), IR (Instruction register), PC (Program counter), TR (Temporary register), SC (Sequence Counter), INPR (Input register), and OUTR (Output register).

Flip-Flops: I, S, E, R, IEN, FGI and FGO

Note: FGI and FGO are corresponding input and output flags which are considered as control flip-flops.

Two decoders: a 3 x 8 operation decoder and a 4 x 16 timing decoder

A 16-bit common bus

Control Logic Gates

The Logic and Adder circuits are connected to the input of AC.

Key takeaway

A program residing in the memory unit of a computer consists of a sequence of instructions. These instructions are executed by the processor by going through a cycle for each instruction.

In a basic computer, each instruction cycle consists of the following phases:

Fetch the instruction from memory.

Decode the instruction.

Read the effective address from memory.

Execute the instruction.

1.4 RTL interpretation of instructions

A digital computer system exhibits an interconnection of digital modules such as registers, decoders, arithmetic elements, and control logic.

These digital modules are interconnected with some common data and control paths to form a completely digital system.

Moreover, digital modules are best defined by the registers and the operations that are performed on the data stored in them.

The operations performed on the data stored in registers are called Micro-operations.

The internal hardware organization of a digital system is best defined by specifying:

The set of registers and the flow of data between them.

The sequence of micro-operations performed on the data which are stored in the registers.

The control paths that initiates the sequence of micro-operation

The Register Transfer Language is the symbolic representation of notations used to specify the sequence of micro-operations.

In a computer system, data transfer takes place between processor registers and memory and between processor registers and input-output systems. These data transfer can be represented by standard notations given below:

Notations R0, R1, R2. . . , and so on represent processor registers.

The addresses of memory locations are represented by names such as LOC, PLACE, MEM, etc.

Input-output registers are represented by names such as DATA IN, DATA OUT, and so on.

The content of the register or memory location is denoted by placing square brackets around the name of the register or memory location.

Key takeaway

A digital computer system exhibits an interconnection of digital modules such as registers, decoders, arithmetic elements, and control logic.

These digital modules are interconnected with some common data and control paths to form a completely digital system.

Moreover, digital modules are best defined by the registers and the operations that are performed on the data stored in them.

The operations performed on the data stored in registers are called Micro-operations.

1.5 Addressing modes

Addressing Modes– The term addressing modes refers to how the operand of an instruction is specified. The addressing mode specifies a rule for interpreting or modifying the address field of the instruction before the operand is executed.

Addressing modes for 8086 instructions are divided into two categories:

1) Addressing modes for data

2) Addressing modes for branch

The 8086 memory addressing modes provide flexible memory access, allowing you to easily access variables, arrays, records, pointers, and other complex data types. The key to good assembly language programming is the proper use of memory addressing modes.

An assembly language program instruction consists of two parts

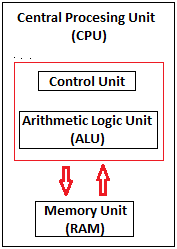
Fig 16 - Assembly language program instruction

The memory address of an operand consists of two components:

IMPORTANT TERMS

The starting address of the memory segment.

Effective address or Offset: An offset is determined by adding any combination of three address elements: displacement, base, and index.

Displacement: It is an 8 bit or 16-bit immediate value given in the instruction.
Base: Contents of the base register, BX or BP.
Index: Content of index register SI or DI.

According to different ways of specifying an operand by 8086 microprocessor, different addressing modes are used by 8086.

Addressing modes used by the 8086 microprocessor are discussed below:

Implied mode: : In implied addressing the operand is specified in the instruction itself. In this mode, the data is 8 bits or 16 bits long and data is the part of instruction. Zero address instructions are designed with implied addressing mode.

Example: CLC (used to reset Carry flag to 0)

Immediate addressing mode (symbol #): In this mode data is present in the address field of instruction. Designed like one address instruction format.
Note: Limitation in the immediate mode is that the range of constants is restricted by the size of the address field.

Example: MOV AL, 35H (move the data 35H into AL register)

Register mode: In register addressing the operand is placed in one of 8 bit or 16-bit general-purpose registers. The data is in the register that is specified by the instruction.
Here one register reference is required to access the data.

Example: MOV AX, CX (move the contents of CX register to AX register)

Register Indirect mode: In this addressing the operand’s offset is placed in any one of the registers BX, BP, SI, DI as specified in the instruction. The effective address of the data is in the base register or an index register that is specified by the instruction.
Here two register reference is required to access the data.

Fig 17 – Register Indirect mode

The 8086 CPUs let you access memory indirectly through a register using the register indirect addressing modes.

MOV AX, [BX](move the contents of memory location s

addressed by the register BX to the register AX)

Auto Indexed (increment mode): Effective address of the operand is the contents of a register specified in the instruction. After accessing the operand, the contents of this register are automatically incremented to point to the next consecutive memory location. (R1)+.

Here one register reference, one memory reference, and one ALU operation is required to access the data.

Example:

Add R1, (R2)+ // OR

R1 = R1 +M[R2]

R2 = R2 + d

Useful for stepping through arrays in a loop. R2 – the start of array d – the size of an element

Auto indexed ( decrement mode): Effective address of the operand is the contents of a register specified in the instruction. Before accessing the operand, the contents of this register are automatically decremented to point to the previous consecutive memory location. –(R1)
Here one register reference, one memory reference, and one ALU operation is required to access the data.

Example:

Add R1,-(R2) //OR

R2 = R2-d

R1 = R1 + M[R2]

Auto decrement mode is the same as an auto-increment mode. Both can also be used to implement a stack as push and pop. Autoincrement and Auto decrement modes are useful for implementing “Last-In-First-Out” data structures.

Direct addressing/ Absolute addressing Mode (symbol [ ]): The operand’s offset is given in the instruction as an 8 bit or 16-bit displacement element. In this addressing mode, the 16 bit effective address of the data is the part of the instruction.
Here only one memory reference operation is required to access the data.

Fig 18 - Example

Example: ADD AL,[0301] //add the contents of offset address 0301 to AL

Indirect addressing Mode (symbol @ or () ): In this mode address field of instruction contains the address of the effective address. Here two references are required.
1st reference to get the effective address.
2nd reference to access the data.

Based on the availability of Effective address, Indirect mode is of two kinds:

Register Indirect: In this mode effective address is in the register, and the corresponding register name will be maintained in the address field of instruction.
Here one register reference, one memory reference is required to access the data.

Memory Indirect: In this mode effective address is in the memory, and the corresponding memory address will be maintained in the address field of instruction.
Here two memory reference is required to access the data.

Indexed addressing mode: The operand’s offset is the sum of the content of an index register SI or DI and an 8 bit or 16-bit displacement.

Example: MOV AX, [SI +05]

Based Indexed Addressing: The operand’s offset is the sum of the content of a base register BX or BP and an index register SI or DI.

Example: ADD AX, [BX+SI]

Based on Transfer of control, addressing modes are:

PC relative addressing mode: PC relative addressing mode is used to implement intra segment transfer of control, In this mode effective address is obtained by adding displacement to PC.

EA= PC + Address field value

PC= PC + Relative value.

3. Base register addressing mode: Base register addressing mode is used to implement inter-segment transfer of control. In this mode effective address is obtained by adding base register value to address field value.

4. EA= Base register + Address field value.

5. PC= Base register + Relative value.

Note:

PC relative nad based register both addressing modes are suitable for program relocation at runtime.

Based register addressing mode is best suitable to write position-independent codes.

Advantages of Addressing Modes

To give programmers to facilities such as Pointers, counters for loop controls, indexing of data, and program relocation.

To reduce the number of bits in the addressing field of the Instruction.

Key takeaway

1.6 Instruction set

Computer instructions are a set of machine language instructions that a particular processor understands and executes. A computer performs tasks based on the instruction provided.

An instruction comprises of groups called fields. These fields include:

The Operation code (Opcode) field specifies the operation to be performed.

The Address field contains the location of the operand, i. e. , register or memory location.

The Mode field specifies how the operand will be located.

Computer Instructions

Fig 19 – Mode field

A basic computer has three instruction code formats which are:

Memory - reference instruction

Input-Output instruction

Computer Instructions

Fig 20 - Memory - reference instruction

In Memory-reference instruction, 12 bits of memory are used to specify an address and one bit to specify the addressing mode 'I'.

Computer Instructions

Fig 21 - Register - reference instruction

The Register-reference instructions are represented by the Opcode 111 with a 0 in the leftmost bit (bit 15) of the instruction.

Note: The Operation code (Opcode) of instruction refers to a group of bits that define arithmetic and logic operations such as add, subtract, multiply, shift, and compliment.

A Register-reference instruction specifies an operation on or a test of the AC (Accumulator) register.

Computer Instructions

Fig 22 - Input-Output instruction

Just like the Register-reference instruction, an Input-Output instruction does not need a reference to memory and is recognized by the operation code 111 with a 1 in the leftmost bit of the instruction. The remaining 12 bits are used to specify the type of input-output operation or test performed.

Note

The three operation code bits in positions 12 through 14 should be equal to 111. Otherwise, the instruction is a memory-reference type, and the bit in position 15 is taken as the addressing mode I.

When the three operation code bits are equal to 111, the control unit inspects the bit in position 15. If the bit is 0, the instruction is a register-reference type. Otherwise, the instruction is an input-output type having bit 1 at position 15.

Instruction Set Completeness

A set of instructions is said to be complete if the computer includes a sufficient number of instructions in each of the following categories:

Arithmetic, logical and shift instructions

A set of instructions for moving information to and from memory and processor registers.

Instructions that controls the program together with instructions that check status conditions.

Input and Output instructions

Arithmetic, logic, and shift instructions provide computational capabilities for processing the type of data the user may wish to employ.

A huge amount of binary information is stored in the memory unit, but all computations are done in processor registers. Therefore, one must possess the capability of moving information between these two units.

Program control instructions such as branch instructions are used to change the sequence in which the program is executed.

Input and Output instructions act as an interface between the computer and the user. Programs and data must be transferred into memory, and the results of computations must be transferred back to the user.

Key takeaway

Computer instructions are a set of machine language instructions that a particular processor understands and executes. A computer performs tasks based on the instruction provided.

An instruction comprises of groups called fields. These fields include:

The Operation code (Opcode) field specifies the operation to be performed.

The Address field contains the location of the operand, i. e. , register or memory location.

The Mode field specifies how the operand will be located.

1.7 Case study – instruction sets of some common CPUs

The Instruction Set Architecture (ISA) is the part of the processor that is visible to the programmer or compiler writer. The ISA serves as the boundary between software and hardware. We will briefly describe the instruction sets found in many of the microprocessors used today. The ISA of a processor can be described using 5 categories:

Operand Storage in the CPU

Where are the operands kept other than in memory?

Number of explicitly named operands

How many operands are named in a typical instruction.

Operand location

Can any ALU instruction operand be located in memory? Or must all operands be kept internally in the CPU?

Operations

What operations are provided in the ISA.

Type and size of operands

What is the type and size of each operand and how is it specified?

Of all the above the most distinguishing factor is the first.

The 3 most common types of ISAs are:

Stack - The operands are implicitly on top of the stack.

Accumulator - One operand is implicitly the accumulator.

General Purpose Register (GPR) - All operands are explicitly mentioned, they are either registers or memory locations.

Let's look at the assembly code of

C = A + B;

in all 3 architectures:

Stack	Accumulator	GPR
PUSH A	LOAD A	LOAD R1, A
PUSH B	ADD B	ADD R1, B
ADD	STORE C	STORE R1, C
POP C	-	-

Not all processors can be neatly tagged into one of the above categories. The i8086 has many instructions that use implicit operands although it has a general register set. The i8051 is another example, it has 4 banks of GPRs but most instructions must have the A register as one of its operands.
What are the advantages and disadvantages of each of these approaches?

Stack

Advantages: Simple Model of expression evaluation (reverse polish). Short instructions.
Disadvantages: A stack can't be randomly accessed Which makes it hard to generate efficient code. The stack itself is accessed every operation and becomes a bottleneck.

Accumulator

Advantages: Short instructions.

Disadvantages: The accumulator is only temporary storage so memory traffic is the highest for this approach.

GPR

Advantages: Makes code generation easy. Data can be stored for long periods in registers.
Disadvantages: All operands must be named leading to longer instructions.

Earlier CPUs were of the first 2 types but in the last 15 years, all CPUs made are GPR processors. The 2 major reasons are that registers are faster than memory, the more data that can be kept internally in the CPU the faster the program will run. The other reason is that registers are easier for a compiler to use.

Reduced Instruction Set Computer (RISC)

As we mentioned before most modern CPUs are of the GPR (General Purpose Register) type. A few examples of such CPUs are the IBM 360, DEC VAX, Intel 80x86, and Motorola 68xxx. But while these CPUs were better than previous stack and accumulator based CPUs they were still lacking in several areas:

Instructions were of varying length from 1 byte to 6-8 bytes. This causes problems with the pre-fetching and pipelining of instructions.

ALU (Arithmetic Logical Unit) instructions could have operands that were memory locations. Because the number of cycles it takes to access memory varies so does the whole instruction. This isn't good for compiler writers, pipelining, and multiple issues.

Most ALU instructions had only 2 operands where one of the operands is also the destination. This means this operand is destroyed during the operation or it must be saved before somewhere.

Thus in the early 80's the idea of RISC was introduced. The SPARC project was started at Berkeley and the MIPS project at Stanford. RISC stands for Reduced Instruction Set Computer. The ISA is composed of instructions that all have the same size, usually 32 bits. Thus they can be pre-fetched and pipelined successfully. All ALU instructions have 3 operands which are only registers. The only memory access is through explicit LOAD/STORE instructions.
Thus C = A + B will be assembled as:

LOAD R1, A

LOAD R2, B

ADD R3, R1, R2

STORE C, R3

Although it takes 4 instructions we can reuse the values in the registers.

Why is this architecture called RISC? What is Reduced about it?
The answer is that to make all instructions the same length the number of bits that are used for the opcode is reduced. Thus fewer instructions are provided. The instructions that were thrown out are the less important string and BCD (binary-coded decimal) operations. Now that memory access is restricted there aren't several kinds of MOV or ADD instructions. Thus the older architecture is called CISC (Complete Instruction Set Computer). RISC architectures are also called LOAD/STORE architectures.

The number of registers in RISC is usually 32 or more. The first RISC CPU the MIPS 2000 has 32 GPRs as opposed to 16 in the 68xxx architecture and 8 in the 80x86 architecture. The only disadvantage of RISC is its code size. Usually, more instructions are needed and there is a waste in short instructions (POP, PUSH).

So why are there still CISC CPUs being developed? Why is Intel spending time and money to manufacture the Pentium II and the Pentium III?
The answer is simple, backward compatibility. The IBM compatible PC is the most common computer in the world. Intel wanted a CPU that would run all the applications that are in the hands of more than 100 million users. On the other hand, Motorola which builds the 68xxx series which was used in the Macintosh made the transition and together with IBM and Apple built the Power PC (PPC) a RISC CPU which is installed in the new Power Macs. As of now Intel and the PC manufacturers are making more money but with Microsoft playing in the RISC field as well (Windows NT runs on Compaq's Alpha) and with the promise of Java the future of CISC isn't clear at all.

Key takeaway

1.8 Signed number representation

Variables such as integers can be represented in two ways, i. e. , signed and unsigned. Signed numbers use a sign flag or can distinguish between negative values and positive values. Whereas unsigned numbers stored only positive numbers but not negative numbers.

Number representation techniques like Binary, Octal, Decimal, and Hexadecimal number representation techniques can represent numbers in both signed and unsigned ways. Binary Number System is one the type of Number Representation techniques. It is most popular and used in digital systems. The binary system is used for representing binary quantities which can be represented by any device that has only two operating states or possible conditions. For example, a switch has only two states: open or close.

In the Binary System, there are only two symbols or possible digit values, i. e. , 0 and 1. Represented by any device that only 2 operating states or possible conditions. Binary numbers are indicated by the addition of either an 0b prefix or a 2 suffix.

Representation of Binary Numbers:

Binary numbers can be represented in the signed and unsigned way. Unsigned binary numbers do not have a sign bit, whereas signed binary numbers use signed bit as well or these can be distinguishable between positive and negative numbers. A signed binary is a specific data type of a signed variable.

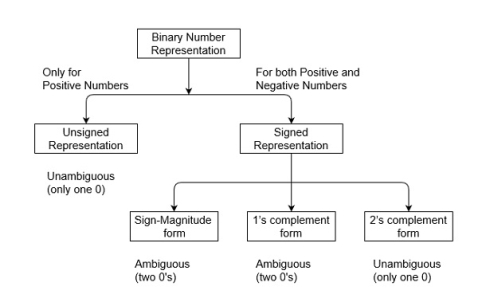
Fig 23 – Binary number representation

1. Unsigned Numbers:

Unsigned numbers don’t have any sign, these can contain the only magnitude of the number. So, the representation of unsigned binary numbers is all positive numbers only. For example, the representation of positive decimal numbers is positive by default. We always assume that there is a positive sign symbol in front of every number.

Representation of Unsigned Binary Numbers:

Since there is no sign bit in this unsigned binary number, so N bit binary number represents its magnitude only. Zero (0) is also an unsigned number. This representation has only one zero (0), which is always positive. Every number in unsigned number representation has only one unique binary equivalent form, so this is an unambiguous representation technique. The range of unsigned binary numbers is from 0 to (2n-1).

Example-1: Represent decimal number 92 in an unsigned binary number.

Simply convert it into a Binary number, it contains the only magnitude of the given number.
= (92)10

= (1x26+0x25+1x24+1x23+1x22+0x21+0x20)10

= (1011100)2

It’s 7 bit binary magnitude of the decimal number 92.

Example-2: Find a range of 5-bit unsigned binary numbers. Also, find the minimum and maximum values in this range.

Since the range of unsigned binary numbers is from 0 to (2n-1). Therefore, the range of 5 bit unsigned binary number is from 0 to (25-1) which is equal from minimum value 0 (i. e., 00000) to maximum value 31 (i. e., 11111).

2. Signed Numbers:

Signed numbers contain a sign flag, this representation distinguishes positive and negative numbers. This technique contains both the sign bit and magnitude of a number. For example, in the representation of negative decimal numbers, we need to put a negative symbol in front of a given decimal number.

Representation of Signed Binary Numbers:

There are three types of representations for signed binary numbers. Because of the extra signed bit, binary number zero has two representations, either positive (0) or negative (1), so ambiguous representation. But 2’s complementation representation is unambiguous because there is no double representation of number 0. These are Sign-Magnitude form, 1’s complement form, and 2’s complement form which are explained below.

2. (a) Sign-Magnitude form:

For n bit binary number, 1 bit is reserved for sign symbol. If the value of the sign bit is 0, then the given number will be positive, else if the value of the sign bit is 1, then the given number will be negative. The Remaining (n-1) bits represent the magnitude of the number. Since the magnitude of number zero (0) is always 0, so there can be two representations of number zero (0), positive (+0), and negative (-0), which depends on the value of sign bit. Hence these representations are ambiguous generally because of two representations of number zero (0). Generally, the sign bit is the most significant bit (MSB) of representation. The range of Sign-Magnitude form is from (2(n-1)-1) to (2(n-1)-1).

For example, range of 6 bit Sign-Magnitude form binary number is from (25-1) to (25-1) which is equal from minimum value -31 (i. e. , 1 11111) to maximum value +31 (i. e. , 0 11111). And zero (0) has two representation, -0 (i. e. , 1 00000) and +0 (i. e. , 0 00000).

2. (b) 1’s complement form:

Since 1’s complement of a number is obtained by inverting each bit of a given number. So, we represent positive numbers in binary form and negative numbers in 1’s complement form. There is an extra bit for sign representation. If the value of the sign bit is 0, then the number is positive and you can directly represent it in simple binary form, but if the value of the sign bit 1, the number is negative and you have to take 1’s complement of given binary number. You can get the negative number by 1’s complement of a positive number and positive number by using 1’s complement of a negative number. Therefore, in this representation, zero (0) can have two representations, that’s why 1’s complement form is also ambiguous. The range of 1’s complement form is from (2(n-1)-1) to (2(n-1)-1) .

For example, range of 6 bit 1’s complement form binary number is from (25-1) to (25-1) which is equal from minimum value -31 (i. e. , 1 00000) to maximum value +31 (i. e. , 0 11111). And zero (0) has two representation, -0 (i. e. , 1 11111) and +0 (i. e. , 0 00000).

2. (c) 2’s complement form:

Since 2’s complement of a number is obtained by inverting each bit of a given number plus 1 to the least significant bit (LSB). So, we represent positive numbers in binary form and negative numbers in 2’s complement form. There is an extra bit for sign representation. If the value of the sign bit is 0, then the number is positive and you can directly represent it in simple binary form, but if the value of the sign bit 1, the number is negative and you have to take 2’s complement of given binary number. You can get the negative number by 2’s complement of a positive number and positive number by directly using simple binary representation. If the value of the most significant bit (MSB) is 1, then take 2’s complement form, else not. Therefore, in this representation, zero (0) has only one (unique) representation which is always positive. The range of 2’s complement form is from (2(n-1)) to (2(n-1)-1).

For example, range of 6 bit 2’s complement form binary number is from (25) to (25-1) which is equal from minimum value -32 (i. e. , 1 00000) to maximum value +31 (i. e. , 0 11111). And zero (0) has two representation, -0 (i. e. , 1 11111) and +0 (i. e. , 0 00000).

Key takeaway

1.9 Fixed and floating-point representations

Digital Computers use a Binary number system to represent all types of information inside the computers. Alphanumeric characters are represented using binary bits (i. e., 0 and 1). Digital representations are easier to design, storage is easy, accuracy and precision are greater.

There are various types of number representation techniques for digital number representation, for example, Binary number system, octal number system, decimal number system, and hexadecimal number system, etc. But the Binary number system is most relevant and popular for representing numbers in the digital computer system.

Storing Real Number

These are structures as below −

There are two major approaches to store real numbers (i. e., numbers with fractional component) in modern computing. These are (i) Fixed-Point Notation and (ii) Floating Point Notation. In fixed-point notation, there are a fixed number of digits after the decimal point, whereas a floating-point number allows for a varying number of digits after the decimal point.

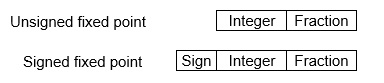
Fixed-Point Representation −

This representation has a fixed number of bits for the integer part and fractional part. For example, if given fixed-point representation is IIII. FFFF, then you can store the minimum value is 0000. 0001 and the maximum value is 9999. 9999. There are three parts of a fixed-point number representation: the sign field, integer field, and fractional field.

We can represent these numbers using:

Signed representation: range from -(2(k-1)-1) to (2(k-1)-1), for k bits.

1’s complement representation: range from -(2(k-1)-1) to (2(k-1)-1), for k bits.

2’s complementation representation: range from -(2(k-1)) to (2(k-1)-1), for k bits.

2’s complementation representation is preferred in the computer system because of its unambiguous property and easier of arithmetic operations.

Example −Assume number is using a 32-bit format which reserves 1 bit for the sign, 15 bits for the integer part, and 16 bits for the fractional part.

Then, -43. 625 is represented as follows:

Where 0 is used to represent + and 1 is used to represent. 000000000101011 is a 15-bit binary value for decimal 43 and 1010000000000000 is a 16-bit binary value for fractional 0. 625.

The advantage of using a fixed-point representation is performance and the disadvantage is a relatively limited range of values that they can represent. So, it is usually inadequate for numerical analysis as it does not allow enough numbers and accuracy. A number whose representation exceeds 32 bits would have to be stored inexactly.

These are above the smallest positive number and largest positive number which can be store in 32-bit representation as given above format. Therefore, the smallest positive number is 2-16 ≈ 0. 000015 approximate and the largest positive number is (215-1)+(1-2-16)=215(1-2-16) =32768, and the gap between these numbers is 2-16.

We can move the radix point either left or right with the help of only integer field is 1.

Floating-Point Representation −

This representation does not reserve a specific number of bits for the integer part or the fractional part. Instead, it reserves a certain number of bits for the number (called the mantissa or significand) and a certain number of bits to say where within that number the decimal place sits (called the exponent).

The floating number representation of a number has two-part: the first part represents a signed fixed-point number called the mantissa. The second part of designates the position of the decimal (or binary) point and is called the exponent. The fixed point mantissa may be a fraction of an integer. Floating -point is always interpreted to represent a number in the following form: Mxre.

Only the mantissa m and the exponent e are physically represented in the register (including their sign). A floating-point binary number is represented similarly except that it uses base 2 for the exponent. A floating-point number is said to be normalized if the most significant digit of the mantissa is 1.

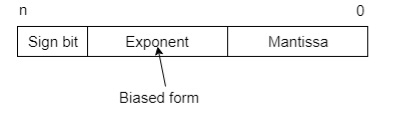
So, the actual number is (-1)s(1+m)x2(e-Bias), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number.

Note that signed integers and exponents are represented by either sign representation, or one’s complement representation, or two’s complement representation.

The floating-point representation is more flexible. Any non-zero number can be represented in the normalized form of ±(1. b1b2b3 . . . )2x2n This is the normalized form of a number x.

Example −Suppose the number is using the 32-bit format: the 1-bit sign bit, 8 bits for the signed exponent, and 23 bits for the fractional part. The leading bit 1 is not stored (as it is always 1 for a normalized number) and is referred to as a “hidden bit”.

Then −53.5 is normalized as -53.5=(-110101.1)2=(-1.101011)x25, which is represented as below,

Where 00000101 is the 8-bit binary value of exponent value +5.

Note that 8-bit exponent ﬁeld is used to store integer exponents -126 ≤ n ≤ 127.

The smallest normalized positive number that ﬁts into 32 bits is (1. 00000000000000000000000)2x2-126=2-126≈1.18x10-38 and the largest normalized positive number that ﬁts into 32 bits is (1. 11111111111111111111111)2x2127=(224-1)x2104 ≈ 3.40x1038. These numbers are represented as below,

The precision of a ﬂoating-point format is the number of positions reserved for binary digits plus one (for the hidden bit). In the examples considered here, the precision is 23+1=24.

The gap between 1 and the next normalized ﬂoating-point number is known as machine epsilon. the gap is (1+2-23)-1=2-23for the above example, but this is the same as the smallest positive ﬂoating-point number because of non-uniform spacing unlike in the ﬁxed-point scenario.

Note that non-terminating binary numbers can be represented in floating-point representation, e. g., 1/3 = (0. 010101 . . . )2 cannot be a ﬂoating-point number as its binary representation is non-terminating.

IEEE Floating point Number Representation −

IEEE (Institute of Electrical and Electronics Engineers) has standardized Floating-Point Representation as the following diagram.

So, the actual number is (-1)s(1+m)x2(e-Bias), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number. The sign bit is 0 for a positive number and 1 for a negative number. Exponents are represented by or two’s complement representation.

According to IEEE 754 standard, the floating-point number is represented in the following ways:

Half Precision (16 bit): 1 sign bit, 5-bit exponent, and 10-bit mantissa

Single Precision (32 bit): 1 sign bit, 8-bit exponent, and 23-bit mantissa

Double Precision (64 bit): 1 sign bit, 11-bit exponent, and 52-bit mantissa

Quadruple Precision (128 bit): 1 sign bit, 15-bit exponent, and 112-bit mantissa

Special Value Representation −

Some special values depended upon different values of the exponent and mantissa in the IEEE 754 standard.

All the exponent bits 0 with all mantissa bits 0 represents 0. If the sign bit is 0, then +0, else -0.

All the exponent bits 1 with all mantissa bits 0 represents infinity. If the sign bit is 0, then +∞, else -∞.

All the exponent bits 0 and mantissa bits non-zero represents a denormalized number.

All the exponent bits 1 and mantissa bits non-zero represents error.

Key takeaway

Digital Computers use a Binary number system to represent all types of information inside the computers. Alphanumeric characters are represented using binary bits (i. e. , 0 and 1). Digital representations are easier to design, storage is easy, accuracy and precision are greater.

1.10 Character representation

Everything represented by a computer is represented by binary sequences.

A common non-integer to be represented is a character. We use standard encodings (binary sequences) to represent characters.

REMEMBER: bit patterns do NOT imply a representation

A 4-bit binary quantity is called a nibble. An 8-bit binary quantity is called a byte.

Many I/O devices work with 8-bit quantities. A standard code ASCII (American Standard for Computer Information Interchange) defines what character is represented by each sequence. You'll look these up in an ASCII table.

Examples:
0100 0001 is 41 (hex) or 65 (decimal). It represents 'A'
0100 0010 is 42 (hex) or 66 (decimal). It represents 'B'

Different bit patterns are used for each different character that needs to be represented.

The code has some nice properties. If the bit patterns are compared, (pretending they represent integers), then 'A' < 'B'. This is good because it helps with sorting things into alphabetical order.

Notes:

'a' (0x61) is different than 'A' (0x41)

'8' (0x38) is different than the integer 8
two's complement repepresentation for 8: 0000 0000 0000 0000 0000 0000 0000 1000
the ASCII character '8': 0011 1000

the digits:
'0' is 48 (decimal) or 0x30
'9' is 57 (decimal) or 0x39

Because of this difference between the integer representation for a character, and the character representation for a character, we constantly need to convert from one to the other.

The computer does arithmetic operations on two's complement integers (and often operations on unsigned integers). The computer can read in or print out a single character representation at a time. So, any time we want to do I/O, we're working with one character at a time and the ASCII representation of the character. Yet, lots of the time, the data represents numbers (just consider integers, for now).

Characters that represent an integer

To read in an integer, and then process the integer, consider an example. Suppose the user types the 4-character sequence 123\n.

The computer can read in a single character at a time. If it reads in exactly 4 characters, then the representations that the computer will have will be

ASCII decimal binary integer 8-bit two's comp.

character hex value desired representation

'1' 0x31 49 00110001 1 00000001

'2' 0x32 50 00110010 2 00000010

'3' 0x33 51 00110011 3 00000011

'\n' 0x0a 10 00001010 (NA) (NA)

From this example, it should be easy to see that conversion of a single ASCII character representation to the desired two's complement integer representation does an integer subtraction.

integer rep desired = ASCII representation - 48

What we need is an algorithm for translating multi-character strings to the integers they represent and visa versa.

ALGORITHM: character string --> integer

the steps:

for '3' '5' '4'

integer = 0

read '3'

translate '3' to 3

integer = integer * 10 + 3 = 3

read '5'

translate '5' to 5

integer = integer * 10 + 5 = 35

read '4'

translate '4' to 4

integer = integer * 10 + 4 = 354

the algorithm:

integer = 0

while there are more characters

get character

digit <- character - 48

integer <- integer * 10 + digit

Going the other direction for translation (integer to set of characters represented, printed out in the correct order), we partially reverse the algorithm.

ALGORITHM: integer --> character string

the steps:

For 354, figure out how many characters there are in

the base desired (3).

Figure out base^(number of characters - 1) (10^2)=100

354 div 100 gives 3

translate 3 to '3' and print it out

354 % 100 gives 54

100/10 = 10

54 div 10 gives 5

translate 5 to '5' and print it out

54 mod 10 gives 4

10/10 = 1

4 div 1 gives 4

translate 4 to '4' and print it out

4 mod 1 gives 0

1/10 = 0, so you're done

written in a form using two loops:

# figure out base^(number of characters - 1)

power_of_base = base

while power_of_base is not large enough

power_of_base = power_of_base * base

while power_of_base != 0

digit = integer / power_of_base

char_to_print = digit + 48

print char_to_print

integer = integer % power_of_base # remainder after integer division

power_of_base = power_of_base / base # quotient

Key takeaway

Everything represented by a computer is represented by binary sequences.

A common non-integer to be represented is a character. We use standard encodings (binary sequences) to represent characters.

REMEMBER: bit patterns do NOT imply a representation

A 4-bit binary quantity is called a nibble. An 8-bit binary quantity is called a byte.

1.11 Computer arithmetic – integer addition and subtraction

Operations we'll get to know:

addition

subtraction

multiplication

division

logical operations (not, and, or, nand, nor, xor, xnor)

shifting

the rules for doing the arithmetic operations vary depending

on what representation is implied.

A LITTLE BIT ON ADDING

----------------------

an overview.

carry in a b | sum carry out

---------------+----------------

0 0 0 | 0 0

0 0 1 | 1 0

0 1 0 | 1 0

0 1 1 | 0 1

1 0 0 | 1 0

1 0 1 | 0 1

1 1 0 | 0 1

1 1 1 | 1 1

a 0011

+b +0001

-- -----

sum 0100

it's just like we do for decimal!

0 + 0 = 0

1 + 0 = 1

1 + 1 = 2 which is 10 in binary, sum is 0 and carry the 1.

1 + 1 + 1 = 3 sum is 1, and carry a 1.

ADDITION

--------

unsigned:

just like the simple addition given.

examples:

100001 00001010 (10)

+011101 +00001110 (14)

------- ---------

111110 00011000 (24)

ignore (throw away) carry out of the msb.

Why? Because computers ALWAYS work with fixed precision.

sign-magnitude:

rules:

- add magnitudes only (do not carry into the sign bit)

- throw away any carry out of the msb of the magnitude

(Due, again, to the fixed precision constraints. )

- add only integers of like sign ( + to + or - to -)

- sign of the result is the same as the sign of the addends

examples:

0 0101 (5) 1 1010 (-10)

+ 0 0011 (3) + 1 0011 (-3)

--------- ---------

0 1000 (8) 1 1101 (-13)

0 01011 (11)

+ 1 01110 (-14)

----------------

don't add! must do subtraction!

one's complement:

by example

00111 (7) 111110 (-1) 11110 (-1)

+ 00101 (5) + 000010 (2) + 11100 (-3)

----------- ------------ ------------

01100 (12) 1 000000 (0) wrong! 1 11010 (-5) wrong!

+ 1 + 1

---------- ----------

000001 (1) right! 11011 (-4) right!

so it seems that if there is a carry out (of 1) from the msb, then

the result will be off by 1, so add 1 again to get the correct

result. (Implementation in HW called an "end around carrry.")

two's complement:

rules:

- just add all the bits

- throw away any carry out of the msb

- (same as for unsigned!)

examples

00011 (3) 101000 111111 (-1)

+ 11100 (-4) + 010000 + 001000 (8)

------------ -------- --------

11111 (-1) 111000 1 000111 (7)

after seeing examples for all these representations, you may see

why 2's complement addition requires simpler hardware than

sign mag. or one's complement addition.

SUBTRACTION

-----------

general rules:

1 - 1 = 0

0 - 0 = 0

1 - 0 = 1

10 - 1 = 1

0 - 1 = borrow!

unsigned:

- it only makes sense to subtract a smaller number from a larger one

examples

1011 (11) must borrow

- 0111 (7)

------------

0100 (4)

sign-magnitude:

- if the signs are the same, then do subtraction

- if signs are different, then change the problem to addition

- compare magnitudes, then subtract smaller from larger

- if the order is switched, then switch the sign too.

- when the integers are of the opposite sign, then do

a - b becomes a + (-b)

a + b becomes a - (-b)

examples

0 00111 (7) 1 11000 (-24)

- 0 11000 (24) - 1 00010 (-2)

-------------- --------------

1 10110 (-22)

do 0 11000 (24)

- 0 00111 (7)

--------------

1 10001 (-17)

(switch sign since the order of the subtraction was reversed)

one's complement:

figure it out on your own

two's complement:

- change the problem to addition!

a - b becomes a + (-b)

- so, get the additive inverse of b, and do addition.

examples

10110 (-10)

- 00011 (3) --> 00011

------------ |

\|/

11100

+ 1

-------

11101 (-3)

so do

10110 (-10)

+ 11101 (-3)

------------

1 10011 (-13)

(throw away carry out)

OVERFLOW DETECTION IN ADDITION

unsigned -- when there is a carry out of the msb

1000 (8)

+1001 (9)

-----

1 0001 (1)

sign-magnitude -- when there is a carry out of the msb of the magnitude

1 1000 (-8)

+ 1 1001 (-9)

-----

1 0001 (-1) (carry out of msb of magnitude)

2's complement -- when the signs of the addends are the same, and the

sign of the result is different

0011 (3)

+ 0110 (6)

----------

1001 (-7) (note that a correct answer would be 9, but

9 cannot be represented in 4 bit 2's complement)

a detail -- you will never get overflow when adding 2 numbers of

opposite signs

OVERFLOW DETECTION IN SUBTRACTION

unsigned -- never

sign-magnitude -- never happen when doing subtraction

2's complement -- we never do subtraction, so use the addition rule

on the addition operation done.

MULTIPLICATION of integers

0 x 0 = 0

0 x 1 = 0

1 x 0 = 0

1 x 1 = 1

-- longhand, it looks just like decimal

-- the result can require 2x as many bits as the larger multiplicand

-- in 2's complement, to always get the right answer without

thinking about the problem, sign extend both multiplicands to

2x as many bits (as the larger). Then take the correct number

of result bits from the least significant portion of the result.

2's complement example:

1111 1111 -1

x 1111 1001 x -7

---------------- ------

11111111 7

00000000

11111111

+ 11111111

----------------

1 00000000111

-------- (correct answer underlined)

0011 (3) 0000 0011 (3)

x 1011 (-5) x 1111 1011 (-5)

------ -----------

0011 00000011

0000 00000000

+ 0011 00000011

--------- 00000011

0100001 00000011

not -15 in any 00000011

representation! + 00000011

------------------

1011110001

take the least significant 8 bits 11110001 = -15

DIVISION of integers

unsigned only!

example of 15 / 3 1111 / 011

To do this longhand, use the same algorithm as for decimal integers.

LOGICAL OPERATIONS

done bitwise

X = 0011

Y = 1010

X AND Y is 0010

X OR Y is 1011

X NOR Y is 0100

X XOR Y is 1001

etc.

SHIFT OPERATIONS

a way of moving bits around within a word

3 types: logical, arithmetic and rotate

(each type can go either left or right)

logical left - move bits to the left, same order

- throw away the bit that pops off the msb

- introduce a 0 into the lsb

00110101

01101010 (logically left shifted by 1 bit)

logical right - move bits to the right, same order

- throw away the bit that pops off the lsb

- introduce a 0 into the msb

00110101

00011010 (logically right-shifted by 1 bit)

arithmetic left - move bits to the left, same order

- throw away the bit that pops off the msb

- introduce a 0 into the lsb

- SAME AS LOGICAL LEFT SHIFT!

arithmetic right - move bits to the right, same order

- throw away the bit that pops off the lsb

- reproduce the original msb into the new msb

- another way of thinking about it: shift the

bits, and then do sign extension

00110101 -> 00011010 (arithmetically right-shifted by 1 bit)

1100 -> 1110 (arithmetically right-shifted by 1 bit)

rotate left - move bits to the left, same order

- put the bit that pops off the msb into the lsb,

so no bits are thrown away or lost.

00110101 -> 01101010 (rotated left by 1 place)

1100 -> 1001 (rotated left by 1 place)

rotate right - move bits to the right, same order

- put the bit that pops off the lsb into the msb,

so no bits are thrown away or lost.

00110101 -> 10011010 (rotated right by 1 place)

1100 -> 0110 (rotated right by 1 place)

SASM INSTRUCTIONS FOR LOGICAL AND SHIFT OPERATIONS

SASM has instructions that do bitwise logical operations and

shifting operations.

lnot x x <- NOT (x)

land x, y x <- (x) AND (y)

lor x, y x <- (x) OR (y)

lxor x, y x <- (x) XOR (y)

llsh x x <- (x), logically left shifted by 1 bit

rlsh x x <- (x), logically right shifted by 1 bit

rash x x <- (x), arithmetically right shifted by 1 bit

rror x x <- (x), rotated right by 1 bit

Key takeaway

carry in a b | sum carry out

---------------+----------------

0 0 0 | 0 0

0 0 1 | 1 0

0 1 0 | 1 0

0 1 1 | 0 1

1 0 0 | 1 0

1 0 1 | 0 1

1 1 0 | 0 1

1 1 1 | 1 1

a 0011

+b +0001

-- -----

sum 0100

It's just like we do for decimal!

0 + 0 = 0

1 + 0 = 1

1 + 1 = 2 which is 10 in binary, sum is 0 and carry the 1.

1 + 1 + 1 = 3 sum is 1, and carry a 1.

1.12 Ripple carry adder

Ripple Carry Adder is a combinational logic circuit.

It is used to add two n-bit binary numbers.

It requires n full adders in its circuit for adding two n-bit binary numbers.

It is also known as an n-bit parallel adder.

4-bit Ripple Carry Adder-

4-bit ripple carries adder is used to add two 4-bit binary numbers.

In Mathematics, any two 4-bit binary numbers A3A2A1A0 and B3B2B1B0 are added as shown below-

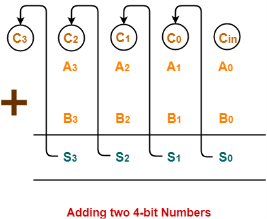
Fig 24 – Adding two 4 bit numbers

Using ripple carry adder, this addition is carried out as shown by the following logic diagram-

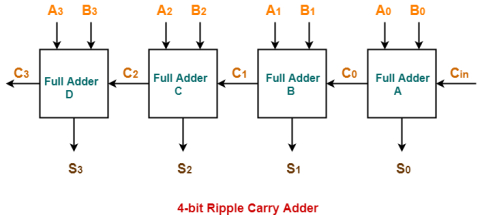
Fig 25 – 4-bit Ripple carry Adder

As shown-

Ripple Carry Adder works in different stages.

Each full adder takes the carry-in as input and produces carry-out and sum bit as output.

The carry-out produced by a full adder serves as carry-in for its adjacent most significant full adder.

When carry-in becomes available to the full adder, it activates the full adder.

After the full adder becomes activated, it comes into operation.

Working Of 4-bit Ripple Carry Adder-

Let-

The two 4-bit numbers are 0101 (A3A2A1A0) and 1010 (B3B2B1B0).

These numbers are to be added using a 4-bit ripple carry adder.

4-bit Ripple Carry Adder carries out the addition as explained in the following stages-

Stage-01:

When Cin is fed as input to the full Adder A, it activates the full adder A.

Then at full adder A, A0 = 1, B0 = 0, Cin = 0.

Full adder A computes the sum bit and carries bit as-

Calculation of S0–

S0 = A0 ⊕ B0 ⊕ Cin

S0 = 1 ⊕ 0 ⊕ 0

S0 = 1

Calculation of C0–

C0 = A0B0 ⊕ B0Cin ⊕ CinA0

C0 = 1. 0 ⊕ 0. 0 ⊕ 0. 1

C0 = 0 ⊕ 0 ⊕ 0

C0 = 0

Stage-02:

When C0 is fed as input to the full adder B, it activates the full adder B.

Then at full adder B, A1 = 0, B1 = 1, C0 = 0.

Full adder B computes the sum bit and carry bit as-

Calculation of S1–

S1 = A1 ⊕ B1 ⊕ C0

S1 = 0 ⊕ 1 ⊕ 0

S1 = 1

Calculation of C1–

C1 = A1B1 ⊕ B1C0 ⊕ C0A1

C1 = 0. 1 ⊕ 1. 0 ⊕ 0. 0

C1 = 0 ⊕ 0 ⊕ 0

C1 = 0

Stage-03:

When C1 is fed as input to the full adder C, it activates the full adder C.

Then at full adder C, A2 = 1, B2 = 0, C1 = 0.

Full adder C computes the sum bit and carry bit as-

Calculation of S2–

S2 = A2 ⊕ B2 ⊕ C1

S2 = 1 ⊕ 0 ⊕ 0

S2 = 1

Calculation of C2–

C2 = A2B2 ⊕ B2C1 ⊕ C1A2

C2 = 1. 0 ⊕ 0. 0 ⊕ 0. 1

C2 = 0 ⊕ 0 ⊕ 0

C2 = 0

Stage-04:

When C2 is fed as input to the full adder D, it activates the full adder D.

Then at full adder D, A3 = 0, B3 = 1, C2 = 0.

Full adder D computes the sum bit and carry bit as-

Calculation of S3–

S3 = A3 ⊕ B3 ⊕ C2

S3 = 0 ⊕ 1 ⊕ 0

S3 = 1

Calculation of C3–

C3 = A3B3 ⊕ B3C2 ⊕ C2A3

C3 = 0. 1 ⊕ 1. 0 ⊕ 0. 0

C3 = 0 ⊕ 0 ⊕ 0

C3 = 0

Thus finally,

Output Sum = S3S2S1S0 = 1111

Output Carry = C3 = 0

Why Ripple Carry Adder is Called So?

In Ripple Carry Adder,

The carry out produced by each full adder serves as carry-in for its adjacent most significant full adder.
Each carries bit ripples or waves into the next stage.
That’s why it is called “Ripple Carry Adder”.

Disadvantages of Ripple Carry Adder-

Ripple Carry Adder does not allow using all the full adders simultaneously.

Each full adder has to necessarily wait until the carry bit becomes available from its adjacent full adder.

This increases the propagation time.

Due to this reason, the ripple carry adder becomes extremely slow.

This is considered to be the biggest disadvantage of using a ripple carry adder.

Key takeaway

Ripple Carry Adder is a combinational logic circuit.

It is used to add two n-bit binary numbers.

It requires n full adders in its circuit for adding two n-bit binary numbers.

It is also known as an n-bit parallel adder.

1.13 Carry look-ahead adder

In the case of parallel adders, the binary addition of two numbers is initiated when all the bits of the augend and the addend must be available at the same time to perform the computation. In a parallel adder circuit, the carry output of each full adder stage is connected to the carry input of the next higher-order stage, hence it is also called a ripple carry type adder.

In such adder circuits, it is not possible to produce the sum and carry outputs of any stage until the input carry occurs. So there will be a considerable time delay in the addition process, which is known as, carry propagation delay. In any combinational circuit, the signal must propagate through the gates before the correct output sum is available in the output terminals.

Fig 26 - Example

Consider the above figure, in which the sum S4 is produced by the corresponding full adder as soon as the input signals are applied to it. But the carry input C4 is not available on its final steady-state value until carry c3 is available at its steady-state value. Similarly, C3 depends on C2 and C2 on C1. Therefore, carry must propagate to all the stages so that output S4 and carry C5 settle their final steady-state value.

The propagation time is equal to the propagation delay of the typical gate times the number of gate levels in the circuit. For example, if each full adder stage has a propagation delay of 20n seconds, then S4 will reach its final correct value after 80n (20 × 4) seconds. If we extend the number of stages for adding more bits then this situation becomes much worse.

So the speed at which the number of bits added in the parallel adder depends on the carry propagation time. However, signals must be propagated through the gates at a given enough time to produce the correct or desired output.

The following are the methods to get the high speed in the parallel adder to produce the binary addition.

By employing faster gates with reduced delays, we can reduce the propagation delay. But there will be a capability limit for every physical logic gate.

Another way is to increase the circuit complexity to reduce the carry delay time. There are several methods available to speed up the parallel adder, one commonly used method employs the principle of look ahead-carry addition by eliminating inter stage carry logic.

Carry-Lookahead Adder

A carry-Lookahead adder is a fast parallel adder as it reduces the propagation delay by more complex hardware, hence it is costlier. In this design, the carry logic over fixed groups of bits of the adder is reduced to two-level logic, which is nothing but a transformation of the ripple carry design.

This method makes use of logic gates to look at the lower order bits of the augend and addend to see whether a higher-order carry is to be generated or not. Let us discuss this in detail.

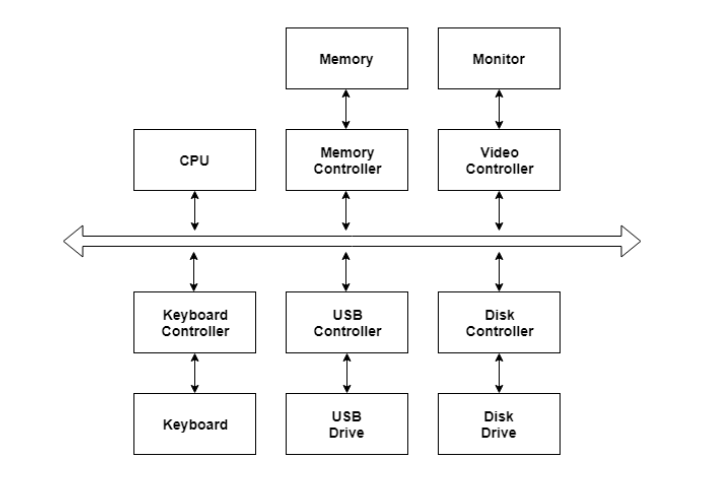
Fig 27 - Example

Consider the full adder circuit shown above with the corresponding truth table. If we define two variables as carry generate Gi and carry propagate Pi then,

Pi = Ai ⊕ Bi

Gi = Ai Bi

The sum output and carry output can be expressed as

Si = Pi ⊕ Ci

C i +1 = Gi + Pi Ci

Where Gi is a carry generate which produces the carry when both Ai, Bi are one regardless of the input carry. Pi is a carry propagate and it is associate with the propagation of carrying from Ci to Ci +1.

The carry output Boolean function of each stage in a 4 stage carry-Lookahead adder can be expressed as

C1 = G0 + P0 Cin

C2 = G1 + P1 C1

= G1 + P1 G0 + P1 P0 Cin

C3 = G2 + P2 C2

= G2 + P2 G1+ P2 P1 G0 + P2 P1 P0 Cin

C4 = G3 + P3 C3

= G3 + P3 G2+ P3 P2 G1 + P3 P2 P1 G0 + P3 P2 P1 P0 Cin

From the above Boolean equations, we can observe that C4 does not have to wait for C3 and C2 to propagate but C4 is propagated at the same time as C3 and C2. Since the Boolean expression for each carry output is the sum of products so these can be implemented with one level of AND gates followed by an OR gate.

The implementation of three Boolean functions for each carry output (C2, C3, and C4) for a carry-Lookahead carry generator is shown in the below figure.

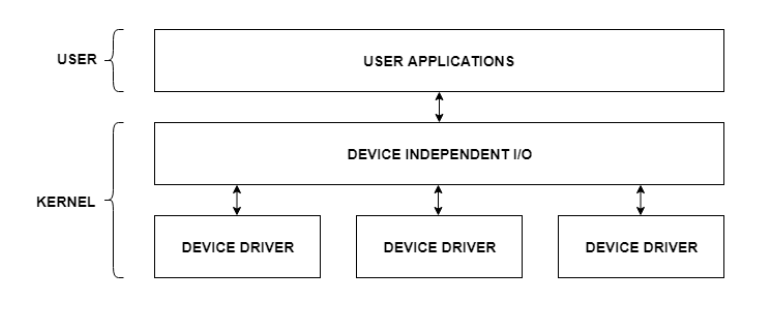
Fig 28 – Look ahead carry generator

Therefore, a 4-bit parallel adder can be implemented with the carry-Lookahead scheme to increase the speed of binary addition as shown below figure. In this, two Ex-OR gates are required by each sum output. The first Ex-OR gate generates Pi variable output and the AND gate generates the Gi variable.

Hence, in two gates levels, all these P’s and G’s are generated. The carry-Lookahead generators allow all these P and G signals to propagate after they settle into their steady-state values and produces the output carriers at a delay of two levels of gates. Therefore, the sum outputs S2 to S4 have equal propagation delay times.

Fig 29 - example

It is also possible to construct 16 bit and 32 bit parallel adders by cascading the number of 4-bit adders with carry logic. A 16-bit carry-Lookahead adder is constructed by cascading the four 4 bit adders with two more gate delays, whereas the 32-bit carry-Lookahead adder is formed by cascading of two 16 bit adders.

In a 16 bit carry-Lookahead adder, 5 and 8 gate delays are required to get C16 and S15 respectively, which are less as compared to the 9 and 10 gate delay for C16 and S15 respectively in cascaded four-bit carry-Lookahead adder blocks. Similarly, in 32-bit adders, 7 and 10 gate delays are required by C32 and S31 which are less compared to 18 and 17 gate delays for the same outputs if the 32-bit adder is implemented by eight 4 bit adders.

Carry-Lookahead Adder ICS

The high-speed carry-Lookahead adders are integrated on integrated circuits in different bit configurations by several manufacturers. There are several individual carry generator ICs are available so that we have to make the connection with logic gates to perform the addition operation.

A typical carry-Lookahead generator IC is 74182 which accepts four pairs of active low carry propagate (as P0, P1, P2, and P3) and carry generate (Go, G1, G2, and G3) signals and an active high input (Cn).

It provides active high carriers (Cn+x, Cn+y, Cn+z) across the four groups of binary adders. This IC also facilitates the other levels of look-ahead by active low propagate and carry generate outputs.

The logic expressions provided by the IC 74182 are

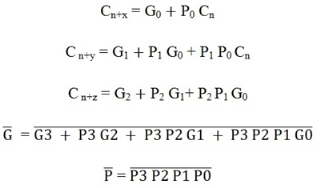
On the other hand, there are many high-speed adder ICs that combine a set of full adders with carry-Lookahead circuitry. The most popular form of such IC is 74LS83/74S283 which is a 4-bit parallel adder high-speed IC that contains four interconnected full adders with a carry-Lookahead circuitry.

The functional symbol for this type of IC is shown below figure. It accepts the two 4 bit numbers as A3A2A1A0 and B3B2B1B0 and input carry Cin0 into the LSB position. This IC produces output sum bits as S3S2S1S0 and the carry output Cout3 into the MSB position.

By cascading two or more parallel adder ICs we can perform the addition of larger binary numbers such as 8 bit, 24-bit, and 32-bit addition.

Key takeaway

1.14 Multiplication – shift-and-add, Booth multiplier, carry-save multiplier

Booth algorithm gives a procedure for multiplying binary integers in signed 2’s complement representation in the efficient way, i. e. , less number of additions/subtractions required. It operates on the fact that strings of 0’s in the multiplier require no addition but just shifting and a string of 1’s in the multiplier from bit weight 2^k to weight 2^m can be treated as 2^(k+1 ) to 2^m.

As in all multiplication schemes, the booth algorithm requires examination of the multiplier bits and shifting of the partial product. Before the shifting, the multiplicand may be added to the partial product, subtracted from the partial product, or left unchanged according to the following rules:

The multiplicand is subtracted from the partial product upon encountering the first least significant 1 in a string of 1’s in the multiplier

The multiplicand is added to the partial product upon encountering the first 0 (provided that there was a previous ‘1’) in a string of 0’s in the multiplier.

The partial product does not change when the multiplier bit is identical to the previous multiplier bit.

Hardware Implementation of Booths Algorithm – The hardware implementation of the booth algorithm requires the register configuration shown in the figure below.

Booth’s Algorithm Flowchart –

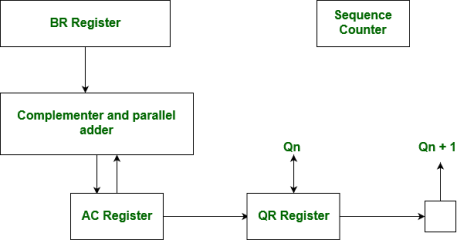
Fig 30 – Booths flowchart

We name the register as A, B, and Q, AC, BR, and QR respectively. Qn designates the least significant bit of multiplier in the register QR. An extra flip-flop Qn+1is appended to QR to facilitate a double inspection of the multiplier. The flowchart for the booth algorithm is shown below.

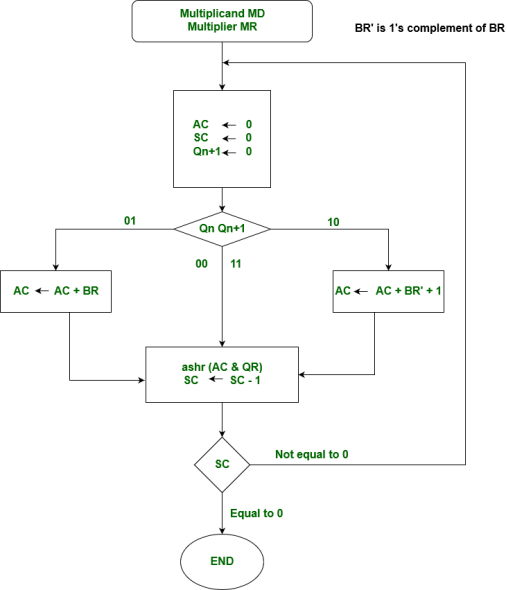
Fig 31 – Booth’s algorithm

AC and the appended bit Qn+1 are initially cleared to 0 and the sequence SC is set to a number n equal to the number of bits in the multiplier. The two bits of the multiplier in Qn and Qn+1are inspected. If the two bits are equal to 10, it means that the first 1 in a string has been encountered. This requires subtraction of the multiplicand from the partial product in AC. If the 2 bits are equal to 01, it means that the first 0 in a string of 0’s has been encountered. This requires the addition of the multiplicand to the partial product in AC.

When the two bits are equal, the partial product does not change. An overflow cannot occur because the addition and subtraction of the multiplicand follow each other. As a consequence, the 2 numbers that are added always have opposite signs, a condition that excludes an overflow. The next step is to shift right the partial product and the multiplier (including Qn+1). This is an arithmetic shift right (ashr) operation in which AC and QR to the right and leaves the sign bit in AC unchanged. The sequence counter is decremented and the computational loop is repeated n times.

Example – A numerical example of the booth’s algorithm is shown below for n = 4. It shows the step by step multiplication of -5 and -7.

MD = -5 = 1011, MD = 1011, MD'+1 = 0101

MR = -7 = 1001

The explanation of the first step is as follows: Qn+1

AC = 0000, MR = 1001, Qn+1 = 0, SC = 4

Qn Qn+1 = 10

So, we do AC + (MD)'+1, which gives AC = 0101

On right shifting AC and MR, we get

AC = 0010, MR = 1100 and Qn+1 = 1

OPERATION	AC	MR	Qn+1	SC
	0000	1001	0	4
AC + MD’ + 1	0101	1001	0
ASHR	0010	1100	1	3
AC + MR	1101	1100	1
ASHR	1110	1110	0	2
ASHR	1111	0111	0	1
AC + MD’ + 1	0010	0011	1	0

The product is calculated as follows:

Product = AC MR

Product = 0010 0011 = 35

Best Case and Worst Case Occurrence:

Best case is when there is a large block of consecutive 1’s and 0’s in the multipliers so that there is a minimum number of logical operations taking place, as in addition and subtraction.

The worst case is when there are pairs of alternate 0’s and 1’s, either 01 or 10 in the multipliers, so that maximum number of additions and subtractions are required.

Key takeaway

As in all multiplication schemes, the booth algorithm requires examination of the multiplier bits and shifting of the partial product.

1.15 Division restoring and non-restoring techniques

In an earlier post Restoring Division learned about restoring division. Now, here perform Non-Restoring division, it is less complex than the restoring one because the simpler operation is involved i. e. addition, and subtraction, also now restoring step is performed. In the method, rely on the sign bit of the register which initially contains zero named as A.

Here is the flow chart is given below.

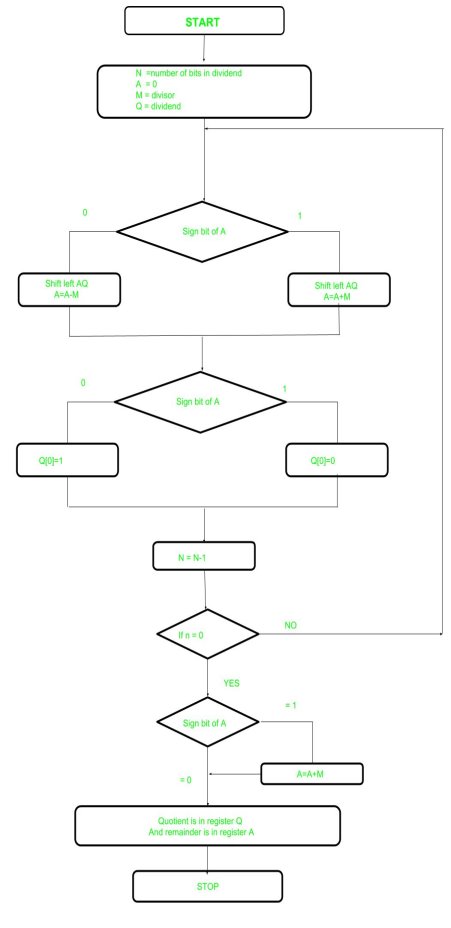
Fig 32 - flowchart

Let’s pick the step involved:

Step-1: First the registers are initialized with corresponding values (Q = Dividend, M = Divisor, A = 0, n = number of bits in dividend)

Step-2: Check the sign bit of register A

Step-3: If it is 1 shift left the content of AQ and perform A = A+M, otherwise shift left AQ and perform A = A-M (means add 2’s complement of M to A and store it to A)

Step-4: Again the sign bit of register A

Step-5: If the sign bit is 1 Q[0] become 0 otherwise Q[0] become 1 (Q[0] means the least significant bit of register Q)

Step-6: Decrements value of N by 1

Step-7: If N is not equal to zero go to Step 2 otherwise go to the next step

Step-8: If sign bit of A is 1 then perform A = A+M

Step-9: Register Q contain quotient and A contain remainder

Examples: Perform Non_Restoring Division for Unsigned Integer

Dividend =11

Divisor =3

-M =11101

N	M	A	Q	Action
4	00011	00000	1011	Start
		00001	011_	Left shift AQ
		11110	011_	A=A-M
3		11110	0110	Q[0]=0
		11100	110_	Left shift AQ
		11111	110_	A=A+M
2		11111	1100	Q[0]=0
		11111	100_	Left Shift AQ
		00010	100_	A=A+M
1		00010	1001	Q[0]=1
		00101	001_	Left Shift AQ
		00010	001_	A=A-M
0		00010	0011	Q[0]=1

Quotient = 3 (Q)

Remainder = 2 (A)

Restoring Division Algorithm For Unsigned Integer

A division algorithm provides a quotient and a remainder when we divide two numbers. They are generally of two types slow algorithm and fast algorithm. Slow division algorithms are restoring, non-restoring, non-performing restoring, SRT algorithm, and under fast comes to Newton–Raphson, and Goldschmidt.

In this article, will be performing restoring algorithm for an unsigned integer. Restoring term is due to fact that the value of register A is restored after each iteration.

Fig 33 - Example

Here, register Q contains quotient and register A contain remainder. Here, the n-bit dividend is loaded in Q, and the divisor is loaded in M. Value of Register is initially kept 0 and this is the register whose value is restored during iteration due to which it is named Restoring.

Let’s pick the step involved:

Step-1: First the registers are initialized with corresponding values (Q = Dividend, M = Divisor, A = 0, n = number of bits in dividend)

Step-2: Then the content of register A and Q is shifted left as if they are a single unit

Step-3: Then the content of register M is subtracted from A and the result is stored in A

Step-4: Then the most significant bit of the A is checked if it is 0 the least significant bit of Q is set to 1 otherwise if it is 1 the least significant bit of Q is set to 0 and the value of register A is restored i. e the value of A before the subtraction with M

Step-5: The value of counter n is decremented

Step-6: If the value of n becomes zero we get of the loop otherwise we repeat from step 2

Step-7: Finally, the register Q contains the quotient, and A contain remainder

Examples:

Perform Division Restoring Algorithm

Dividend = 11

Divisor = 3

n	M	A	Q	Operation
4	00011	00000	1011	initialize
	00011	00001	011_	shift left AQ
	00011	11110	011_	A=A-M
	00011	00001	0110	Q[0]=0 And restore A
3	00011	00010	110_	shift left AQ
	00011	11111	110_	A=A-M
	00011	00010	1100	Q[0]=0
2	00011	00101	100_	shift left AQ
	00011	00010	100_	A=A-M
	00011	00010	1001	Q[0]=1
1	00011	00101	001_	shift left AQ
	00011	00010	001_	A=A-M
	00011	00010	0011	Q[0]=1

Remember to restore the value of A most significant bit of A is 1. As that register Q contains the quotient, i. e. 3 and register A contain remainder 2.

Key takeaway

1.16 Floating-point arithmetic

The objectives of this module are to discuss the need for floating-point numbers, the standard representation used for floating-point numbers, and discuss how the various floating-point arithmetic operations of addition, subtraction, multiplication, and division are carried out.

Floating-point numbers and operations

Representation

When you have to represent very small or very large numbers, a fixed point representation will not do. The accuracy will be lost. Therefore, you will have to look at floating-point representations, where the binary point is assumed to be floating. When you consider a decimal number 12. 34 * 107, this can also be treated as 0. 1234 * 109, where 0. 1234 is the fixed-point mantissa. The other part represents the exponent value and indicates that the actual position of the binary point is 9 positions to the right (left) of the indicated binary point in the fraction. Since the binary point can be moved to any position and the exponent value adjusted appropriately, it is called a floating-point representation. By convention, you generally go in for a normalized representation, wherein the floating-point is placed to the right of the first nonzero (significant) digit. The base need not be specified explicitly and the sign, the significant digits, and the signed exponent constitute the representation.

The IEEE (Institute of Electrical and Electronics Engineers) has produced a standard for floating-point arithmetic. This standard specifies how single-precision (32 bit) and double-precision (64 bit) floating-point numbers are to be represented, as well as how arithmetic should be carried out on them. The IEEE single-precision floating-point standard representation requires a 32-bit word, which may be represented as numbered from 0 to 31, left to right. The first bit is the sign bit, S, the next eight bits are the exponent bits, ‘E’, and the final 23 bits are the fraction ‘F’. Instead of the signed exponent E, the value stored is an unsigned integer E’ = E + 127, called the excess-127 format. Therefore, E’ is in the range 0 £ E’ £ 255.

S E’E’E’E’E’E’E’E’ FFFFFFFFFFFFFFFFFFFFFFF

0 1 8 9 31

The value V represented by the word may be determined as follows:

If E’ = 255 and F is nonzero, then V = NaN (“Not a number”)

If E’ = 255 and F is zero and S is 1, then V = -Infinity

If E’ = 255 and F is zero and S is 0, then V = Infinity

If 0 < E< 255 then V =(-1)**S * 2 ** (E-127) * (1. F) where “1. F” is intended to represent the binary number created by prefixing F with an implicit leading 1 and a binary point.

If E’ = 0 and F is nonzero, then V = (-1)**S * 2 ** (-126) * (0. F). These are “unnormalized” values.

If E’= 0 and F is zero and S is 1, then V = -0

If E’ = 0 and F is zero and S is 0, then V = 0

For example,

0 00000000 00000000000000000000000 = 0

1 00000000 00000000000000000000000 = -0

0 11111111 00000000000000000000000 = Infinity

1 11111111 00000000000000000000000 = -Infinity

0 11111111 00000100000000000000000 = NaN

1 11111111 00100010001001010101010 = NaN

0 10000000 00000000000000000000000 = +1 * 2**(128-127) * 1. 0 = 2

0 10000001 10100000000000000000000 = +1 * 2**(129-127) * 1. 101 = 6. 5

1 10000001 10100000000000000000000 = -1 * 2**(129-127) * 1. 101 = -6. 5

0 00000001 00000000000000000000000 = +1 * 2**(1-127) * 1. 0 = 2**(-126)

0 00000000 10000000000000000000000 = +1 * 2**(-126) * 0. 1 = 2**(-127)

0 00000000 00000000000000000000001 = +1 * 2**(-126) *

0. 00000000000000000000001 = 2**(-149) (Smallest positive value)

(unnormalized values)

Double Precision Numbers:

The IEEE double-precision floating point standard representation requires a 64-bit word, which may be represented as numbered from 0 to 63, left to right. The first bit is the sign bit, S, the next eleven bits are the excess-1023 exponent bits, E’, and the final 52 bits are the fraction ‘F’:

S E’E’E’E’E’E’E’E’E’E’E’

FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF

0 1 11 12

The value V represented by the word may be determined as follows:

If E’ = 2047 and F is nonzero, then V = NaN (“Not a number”)

If E’= 2047 and F is zero and S is 1, then V = -Infinity

If E’= 2047 and F is zero and S is 0, then V = Infinity

If 0 < E’< 2047 then V = (-1)**S * 2 ** (E-1023) * (1. F) where “1. F” is intended to represent the binary number created by prefixing F with an implicit leading 1 and a binary point.

If E’= 0 and F is nonzero, then V = (-1)**S * 2 ** (-1022) * (0. F) These are “unnormalized” values.

If E’= 0 and F is zero and S is 1, then V = – 0

If E’= 0 and F is zero and S is 0, then V = 0

Arithmetic unit

Arithmetic operations on floating-point numbers consist of addition, subtraction, multiplication, and division. The operations are done with algorithms similar to those used on sign-magnitude integers (because of the similarity of representation) — for example, only add numbers of the same sign. If the numbers are of opposite sign, must do subtraction.

ADDITION

Example on decimal value given in scientific notation:

3. 25 x 10 ** 3

+ 2. 63 x 10 ** -1

—————–

first step: align decimal points

second step: add

3. 25 x 10 ** 3

+ 0. 000263 x 10 ** 3

——————–

3. 250263 x 10 ** 3

(presumes the use of infinite precision, without regard for accuracy)

third step: normalize the result (already normalized!)

Example on floating pt. the value is given in binary:

. 25 = 0 01111101 00000000000000000000000

100 = 0 10000101 10010000000000000000000

To add this fl. pt. representations,

step 1: align radix points

shifting the mantissa left by 1 bit decreases the exponent by 1

shifting the mantissa right by 1 bit increases the exponent by 1

we want to shift the mantissa right because the bits that fall off the end should come from the least significant end of the mantissa

-> choose to shift the. 25 since we want to increase its exponent.

-> shift by 10000101

-01111101

———

00001000 (8) places.

0 01111101 00000000000000000000000 (original value)

0 01111110 10000000000000000000000 (shifted 1 place)

(note that hidden bit is shifted into msb of mantissa)

0 01111111 01000000000000000000000 (shifted 2 places)

0 10000000 00100000000000000000000 (shifted 3 places)

0 10000001 00010000000000000000000 (shifted 4 places)

0 10000010 00001000000000000000000 (shifted 5 places)

0 10000011 00000100000000000000000 (shifted 6 places)

0 10000100 00000010000000000000000 (shifted 7 places)

0 10000101 00000001000000000000000 (shifted 8 places)

step 2: add (don’t forget the hidden bit for the 100)

0 10000101 1. 10010000000000000000000 (100)

+ 0 10000101 0. 00000001000000000000000 (. 25)

—————————————

0 10000101 1. 10010001000000000000000

step 3: normalize the result (get the “hidden bit” to be a 1)

It already is for this example.

result is

0 10000101 10010001000000000000000

SUBTRACTION

Same as addition as far as alignment of radix points

Then the algorithm for the subtraction of sign mag. numbers take over.

before subtracting,

compare magnitudes (don’t forget the hidden bit!)

change sign bit if the order of operands is changed.

don’t forget to normalize the number afterward.

MULTIPLICATION

Example on decimal values given in scientific notation:

3. 0 x 10 ** 1

+ 0. 5 x 10 ** 2

—————–

Algorithm: multiply mantissas

add exponents

3. 0 x 10 ** 1

+ 0. 5 x 10 ** 2

—————–

1. 50 x 10 ** 3

Example in binary: Consider a mantissa that is only 4 bits.

0 10000100 0100

x 1 00111100 1100

Add exponents:

always add true exponents (otherwise the bias gets added in twice)

DIVISION

It is similar to multiplication.

do unsigned division on the mantissa (don’t forget the hidden bit)

subtract TRUE exponents

The organization of a floating-point adder unit and the algorithm is given below.

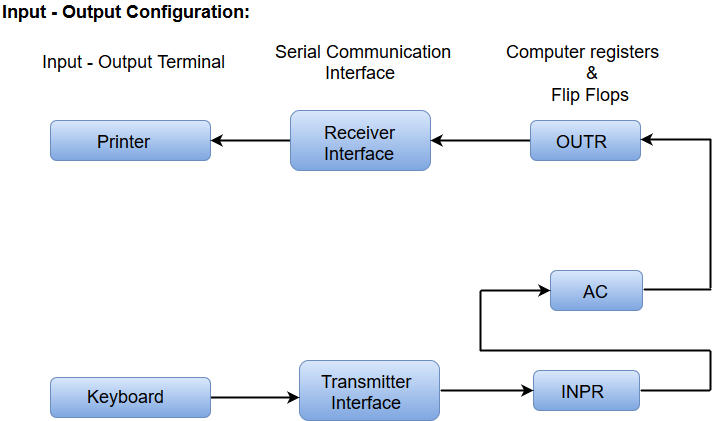
The floating-point multiplication algorithm is given below. A similar algorithm based on the steps discussed before can be used for division.

Fig 34 – division algorithm

Rounding

The floating-point arithmetic operations discussed above may produce a result with more digits than can be represented in 1. M. In such cases, the result must be rounded to fit into the available number of M positions. The extra bits that are used in intermediate calculations to improve the precision of the result are called guard bits. It is only a tradeoff of hardware cost (keeping extra bits) and speed versus accumulated rounding error because finally, these extra bits have to be rounded off to conform to the IEEE standard.

Rounding Methods:

Truncate

– Remove all digits beyond those supported

– 1. 00100 -> 1. 00

Round up to the next value

– 1. 00100 -> 1. 01

Round down to the previous value

– 1. 00100 -> 1. 00

– Differs from Truncate for negative numbers

Round-to-nearest-even

– Rounds to the even value (the one with an LSB of 0)

– 1. 00100 -> 1. 00

– 1. 01100 -> 1. 10

– Produces zero average bias

– Default mode

A product may have twice as many digits as the multiplier and multiplicand

– 1. 11 x 1. 01 = 10. 0011

For round-to-nearest-even, we need to know the value to the right of the LSB (round bit) and whether any other digits to the right of the round digit are 1’s (the sticky bit is the OR of these digits). The IEEE standard requires the use of 3 extra bits of less significance than the 24 bits (of mantissa) implied in the single-precision representation – guard bit, round bit, and sticky bit. When a mantissa is to be shifted to align radix points, the bits that fall off the least significant end of the mantissa go into these extra bits (guard, round, and sticky bits). These bits can also be set by the normalization step in multiplication, and by extra bits of the quotient (remainder) in the division. The guard and round bits are just 2 extra bits of precision that are used in calculations. The sticky bit is an indication of what is/could be in lesser significant bits that are not kept. If a value of 1 ever is shifted into the sticky bit position, that sticky bit remains a 1 (“sticks” at 1), despite further shifts.

To summarize, in his module we have discussed the need for floating-point numbers, the IEEE standard for representing floating-point numbers, Floating-point addition/subtraction, multiplication, division, and the various rounding methods.

Key takeaway

References:

1. “Computer Organization and Design: The Hardware/Software Interface”, 5th Edition by David A. Patterson and John L. Hennessy, Elsevier.

2. “Computer Organization and Embedded Systems”, 6th Edition by Carl Hamacher, McGraw Hill Higher Education.

3. “Computer Architecture and Organization”, 3rd Edition by John P. Hayes, WCB/McGraw-Hill

4. “Computer Organization and Architecture: Designing for Performance”, 10th Edition by William Stallings, Pearson Education.

5. “Computer System Design and Architecture”, 2nd Edition by Vincent P. Heuring and Harry F. Jordan, Pearson Education.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined