UNIT 8
TORSIONAL MOTION
Torsion of circular shafts
Definition of Torsion: Consider a shaft rigidly clamped at one end and twisted at the other end by a torque T = F.d applied in a plane perpendicular to the axis of the bar such a shaft is said to be in torsion.
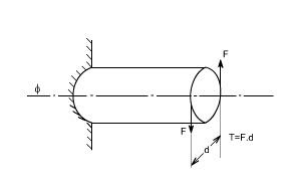
Effects of Torsion: The effects of a torsional load applied to a bar are
(i) To impart an angular displacement of one end cross section with respect to the other end.
(ii) To setup shear stresses on any cross section of the bar perpendicular to its axis.
GENERATION OF SHEAR STRESSES
The physical understanding of the phenomena of setting up of shear stresses in a shaft subjected to a torsion may be understood from the figure.
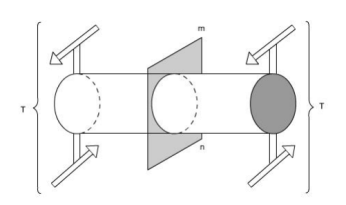
Fig: Here the cylindrical member or a shaft is in static equilibrium where T is the resultant external torque acting on the member. Let the member be imagined to be cut by some imaginary plane mn'.
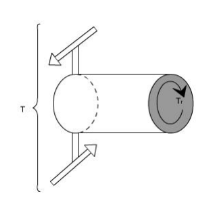
Fig 2: When the plane mn' cuts remove the portion on R.H.S. And we get a fig 2. Now since the entire member is in equilibrium, therefore, each portion must be in equilibrium. Thus, the member is in equilibrium under the action of resultant external torque T and developed resisting Torque Tr
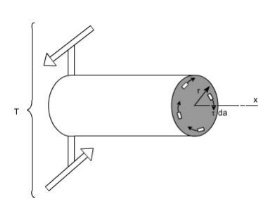
.
Fig 3: The Figure shows that how the resisting torque Tr is developed. The resisting torque Tr is produced by virtue of an infinites mal shear forces acting on the plane perpendicular to the axis of the shaft. Obviously such shear forces would be developed by virtue of sheer stresses.
Therefore we can say that when a particular member (say shaft in this case) is subjected to a torque, the result would be that on any element there will be shear stresses acting. While on other faces the complementary sheer forces come into picture. Thus, we can say that when a member is subjected to torque, an element of this member will be subjected to a state of pure shear.
Shaft: The shafts are the machine elements which are used to transmit power in machines.
Twisting Moment: The twisting moment for any section along the bar / shaft is defined to be the
Algebraic sum of the moments of the applied couples that lie to one side of the section under consideration. The choice of the side in any case is of course arbitrary.
Shearing Strain: If a generator a b is marked on the surface of the unloaded bar, then after the twisting moment 'T' has been applied this line moves to ab'. The angle measured in radians, between the final and original positions of the generators is defined as the shearing strain at the surface of the bar or shaft. The same definition will hold at any interior point of the bar.
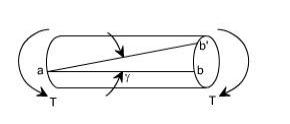
Modulus of Elasticity in shear: The ratio of the shear stress to the shear strain is called the modulus of elasticity in shear OR Modulus of Rigidity and in represented by the symbol
Angle of Twist: If a shaft of length L is subjected to a constant twisting moment T along its length, than the angle through which one end of the bar will twist relative to the other is known is the angle of twist.
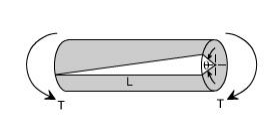
Despite the differences in the forms of loading, we see that there are number of similarities between bending and torsion, including for example, a linear variation of stresses and strain with position.
In torsion the members are subjected to moments (couples) in planes normal to their axes.
For the purpose of designing a circular shaft to withstand a given torque, we must develop an equation giving the relation between twisting moment, maximum shear stress produced, and a quantity representing the size and shape of the cross-sectional area of the shaft.
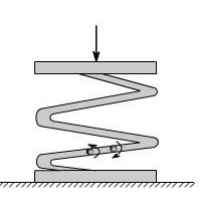
Not all torsion problems, involve rotating machinery, however, for example some types of
Vehicle suspension system employ torsional springs. Indeed, even coil springs are really curved members in torsion as shown in figure.
Many torque carrying engineering members are cylindrical in shape. Examples are drive shafts, bolts and screw drivers.
Torsion equation or torsion constant is defined as the geometrical property of a bar’s cross-section that is involved in the axis of the bar that has a relationship between the angle of twist and applied torque whose SI unit is m4. The torsion equation is given as follows:
T/J= τ/r=GΘ/L
Torsion equation derivation
Following are the assumptions made for the derivation of torsion equation:
- The material is homogeneous (elastic property throughout)
- The material should follow Hook’s law
- The material should have shear stress proportional to shear strain
- The cross-sectional area should be plane
- The circular section should be circular
- Every diameter of the material should rotate through the same angle
- The stress of the material should not exceed the elastic limit
Consider a solid circular shaft with radius R that is subjected to a torque T at one end and the other end under the same torque.
T = Maximum twisting torque or twisting moment
D = Diameter of shaft
R = Radius of shaft
J = Polar moment of Inertia
τ= Maximum Permissible Shear stress (Fixed for given material)
G = Modulus of rigidity
θ= Angle of twist (Radians) = angle D'OD L = Length of shaft.
?= Angle D'CD = Angle of Shear strain
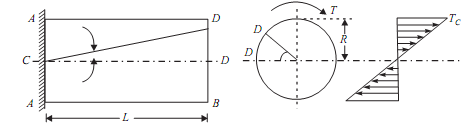
Than Torsion equation is: T/J = τ/R = G. θ /L
Let the shaft is subjected to a torque or twisting moment 'T'. And hence every C.S. Of this shaft will be subjected to shear stress.
Now distortion at the outer surface = DD'
Shear strain at outer surface = Distortion/Unit length tan? = DD'/CD
i.e. shear stress at the outer surface (tan? ) = DD'/L or = DD'/L ...(i)
Now DD' = R.θ or ?= R .θ /L ...(ii)
Now G = Shear stress induced/shear strain produced
G = τ / (R. θ /L);
Or; τ/R = G. θ /L …..(A);
This equation is called Stiffness equation.
Hear G, θ , L are constant for a given torque 'T'. That is proportional to R
If τ r be the intensity of shear stress at any layer at a distance 'r' from canter of the shaft, then;

Now from equation (ii) T = (τ/R) J
Or τ/R = T/J; ..(B)
This equation is called as strength equation
The combined equation A and B; we get
T/J = τ/R = G. θ /L
This equation is called as Torsion equation.
From the relation T/J = τ/R We have T = τ .J/R = τ .ZP
For the given shaft IP and R are constants and IP/R is thus constant and is called as POLAR MODULUS(ZP). Of the shaft section.
Polar modulus of section is thus measure of strength of shaft in the torsion.
TORSIONAL RIGIDITY or Torsional Stiffness (K): = G.J/L = T/θ
Deformation of a Circular Bar
Consider a bar or shaft of circular cross section twisted by a couple T, assume the left-hand end is fixed and the right-hand end will rotate a small angle ϕ, called angle of twist if every cross section has the same radius and subjected to the same torque, the angle ϕ (x) will vary linearly between ends under twisting deformation, it is assumed
1. Plane section remains plane
2. Radii remaining straight and the cross sections remaining plane and circular
3. If ϕ is small, neither the length L nor its radius will change consider an element of the bar dx, on its outer surface we choose an small element abcd,
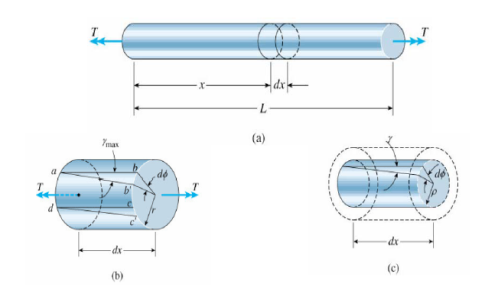
During twisting the element rotate a small angle d, the element is in
a state of pure shear, and deformed into ab'c'd, its shear strain γmax is
γmax = bb’/ab = r d ϕ / dx
d ϕ / dx represents the rate of change of the angle of twist ϕ, denote θ= d ϕ / dx as the angle of twist per unit length or the rate of twist, then γmax = r θ in general, ϕ and θ are function of x, in the special case of pure torsion, θ is constant along the length (every cross section is subjected to the same torque) θ = ϕ/L and γmax = rθ/L and the shear strain inside the bar can be obtained
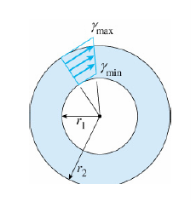
γ = ρ.θ=ρ. γmax / r
γmin = r1 /r2 γmax
For a circular tube, it can be obtained .the above relationships are based only upon geometric concepts, they are valid for a circular bar of any material, elastic or inelastic, linear or nonlinear.
Torsion or twisting moment
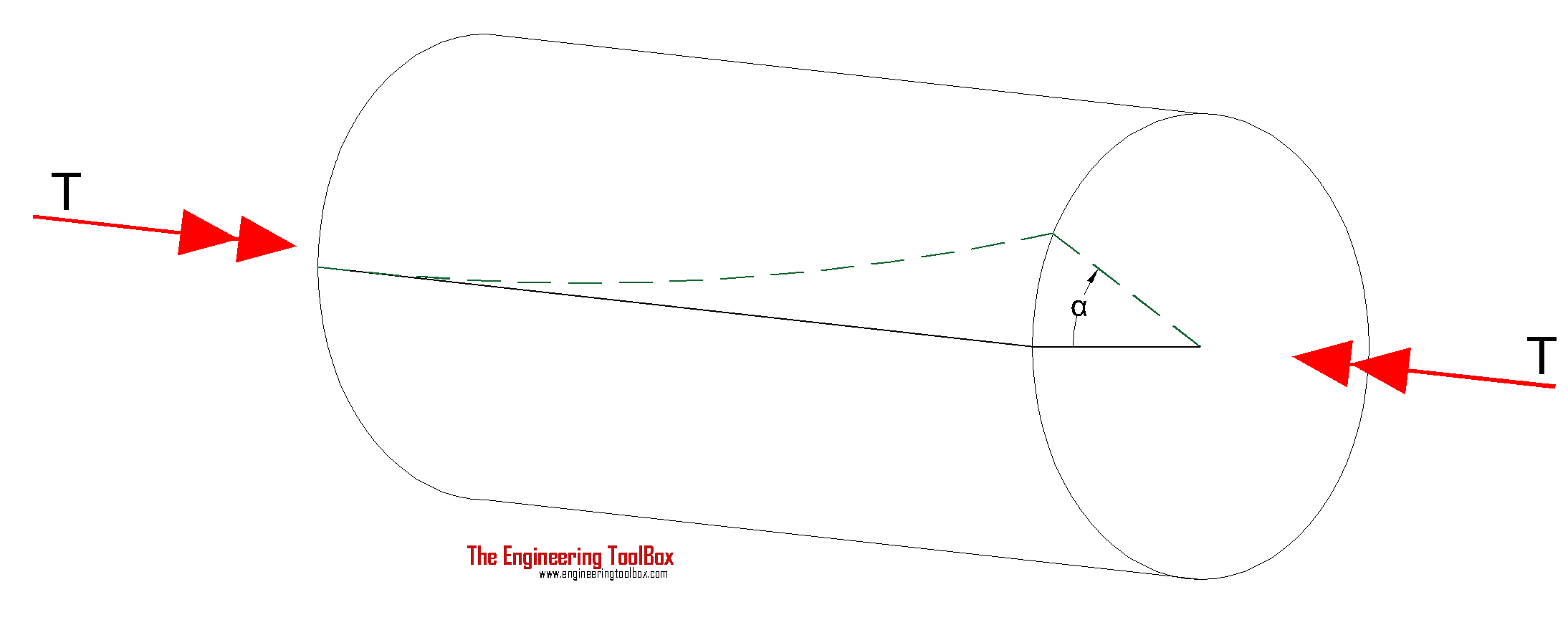
A shaft will said to be in torsion, if it will be subjected with two equal and opposite torques applied at its two ends. When a shaft will be subjected to torsion or twisting moment, there will be developed shear stress and shear strain in the shaft material.
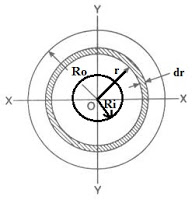
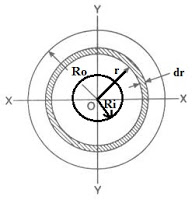
We will discuss here one case of a hollow circular shaft which will be subjected to torsion and we will secure here the expression for maximum torque transmitted by a hollow circular shaft.
We have following information from above figure
Ro = Outer radius of the hollow circular shaft
Ri = Inner radius of the hollow circular shaft
Do = Outer diameter of the hollow circular shaft
Di = Inner diameter of the hollow circular shaft
Dr = Thickness of small elementary circular ring
r = Radius of the small elementary of circular ring
q = Shear stress at a radius r from the centre of the hollow circular shaft
τ = Maximum shear stress at outer surface of shaft
DA = Area of the small elementary of circular ring
DA = 2П x r x dr
Shear stress, at a radius r from the centre, could be determined as mentioned here
q/ r = τ / Ro
q = τ x r/ Ro
Turning force due to shear stress at a radius r from the centre could be determined as mentioned here
DF = q x dA
DF = τ x r/ Ro x 2П x r x dr
DF = τ/ Ro x 2П r2dr
Twisting moment at the circular elementary ring could be determined as mentioned here
DT = Turning force x r
DT = τ/ Ro x 2П r3dr
Total torque could be easily determined by integrating the above equation between limits Ri and Ro.
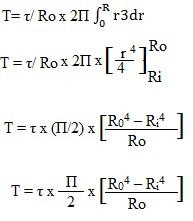
Therefore total torque transmitted by a hollow circular shaft will be given by following formula
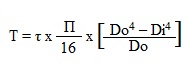
Circular Shaft and Maximum Moment or Torque
Maximum moment in a circular shaft can be expressed as:
Tmax = τmax J / R (1)
Where
Tmax = maximum twisting torque (Nm, lbf ft)
τmax = maximum shear stress (Pa, lbf/ft2)
R = radius of shaft (m, ft)
Combining (2) and (3) for a solid shaft
Tmax = (π / 16) τmax D3 (1b)
Combining (2) and (3b) for a hollow shaft
Tmax = (π / 16) τmax (D4 - d4) / D (1c)
Circular Shaft and Polar Moment of Inertia
Polar Moment of Inertia of a circular solid shaft can be expressed as
J = π R4 / 2
= π (D / 2)4 / 2
= π D4 / 32 (2)
Where
D = shaft outside diameter (m, in)
Polar Moment of Inertia of a circular hollow shaft can be expressed as
J = π (D4 - d4) / 32 (2b)
Where
d = shaft inside diameter (m, ft)
Diameter of a Solid Shaft
Diameter of a solid shaft can calculated by the formula
D = 1.72 (Tmax / τmax)1/3 (3)
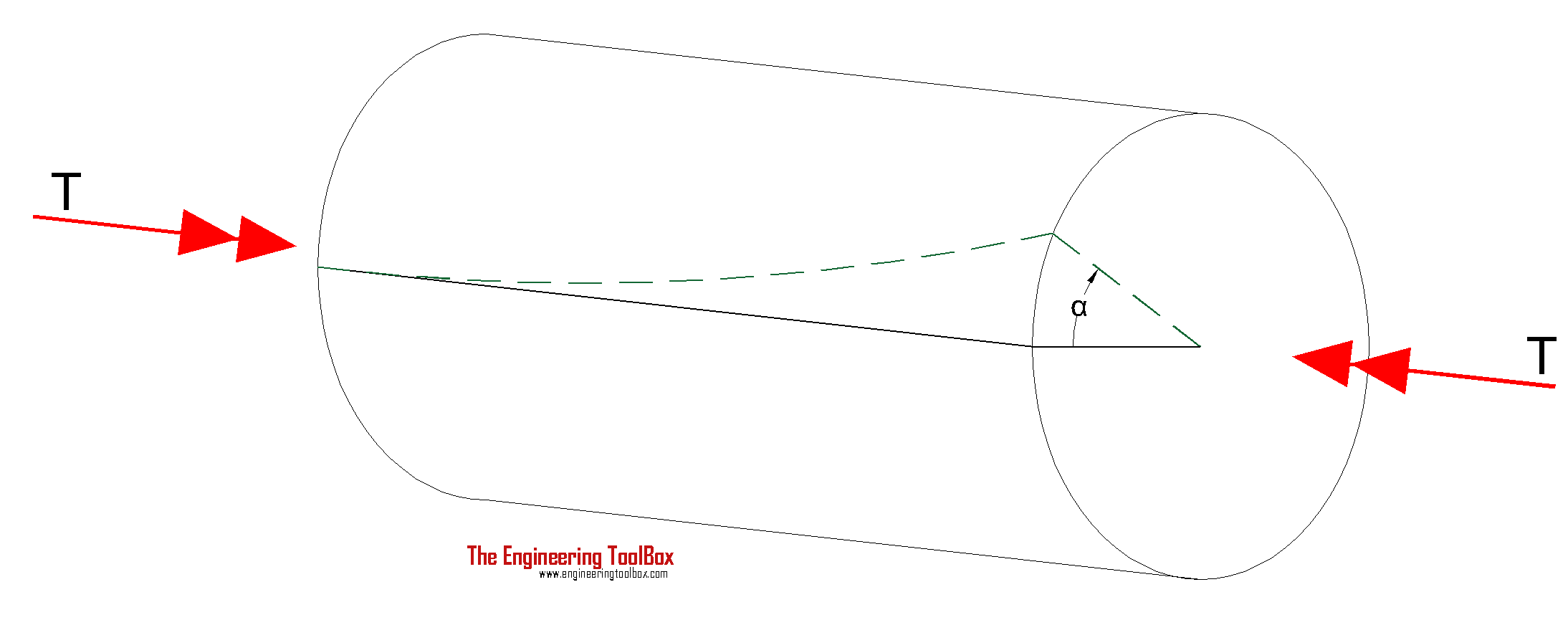
Torsional Deflection of Shaft
The angular deflection of a torsion shaft can be expressed as
α = L T / (J G) (4)
Where
α = angular shaft deflection (radians)
L = length of shaft (m, ft)
G = Shear Modulus of Rigidity - or Modulus of Rigidity (Pa, psf)
The angular deflection of a torsion solid shaft can be expressed as
α = 32 L T / (G π D4) (4a)
The angular deflection of a torsion hollow shaft can be expressed as
α = 32 L T / (G π (D4- d4)) (4b)
The angle in degrees can be achieved by multiplying the angle θ in radians with 180 / π.
Solid shaft (π replaced)
αdegrees ≈ 584 L T / (G D4) (5a)
Hollow shaft (π replaced)
αdegrees ≈ 584 L T / (G (D4- d4) (5b)
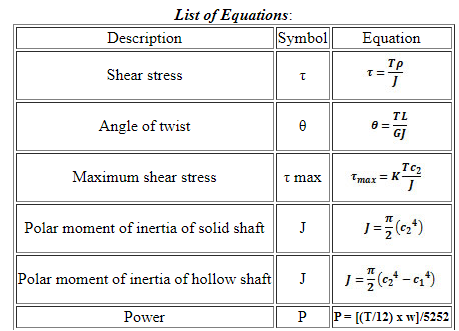
Shaft Cross Section Area | Maximum Torsional | Nomenclature | |
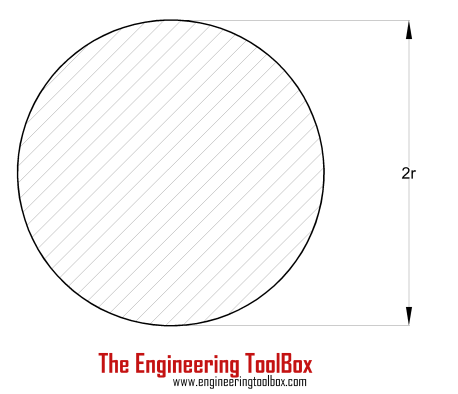
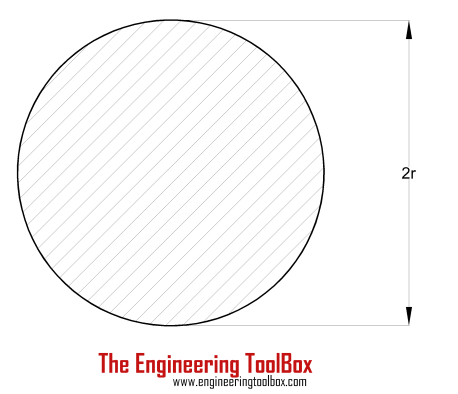 | Solid Cylinder Shaft | (π / 16) τmax (2 r)3 = (π / 16) τmax D3 |
|
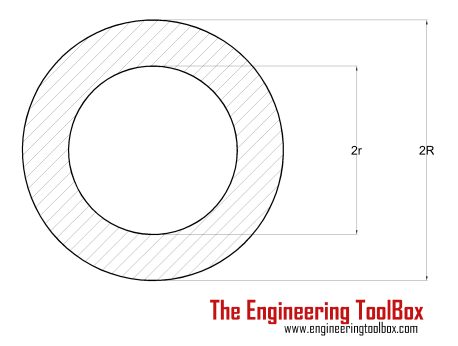
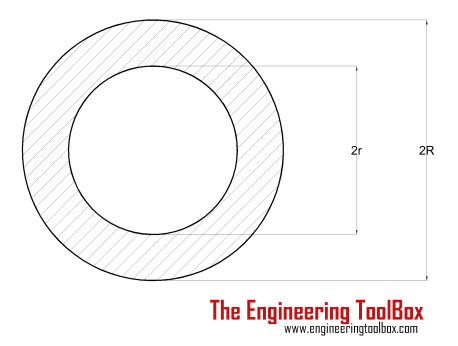 | Hollow Cylinder Shaft | (π / 16) τmax ((2 R)4 - (2 r)4) / (2 R) = (π / 16) τmax (D4 - d4) / D |
|
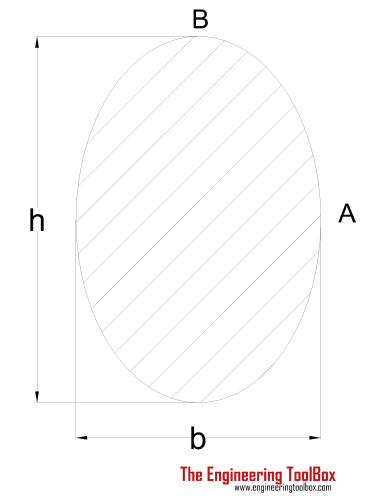
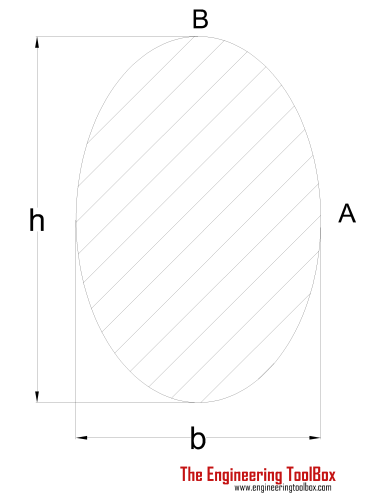 | Ellipse Shaft | (π / 16) τmax b2 h | h = "height" of shaft |
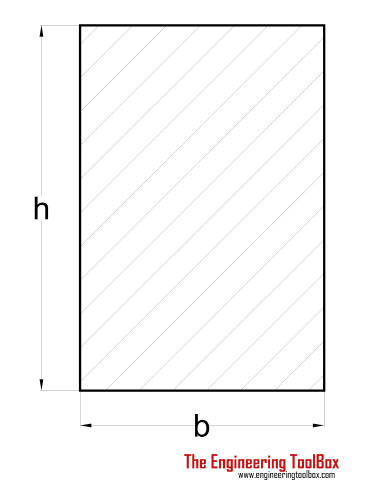 | Rectangle Shaft | (2 / 9) τmax b2 h | h > b |
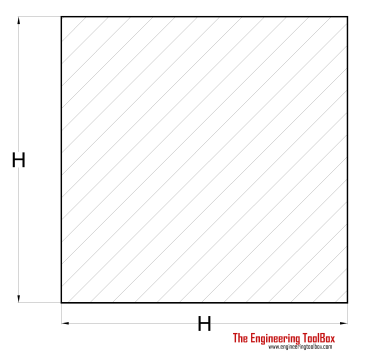 | Square Shaft | (2 / 9) τmax H3 |
|
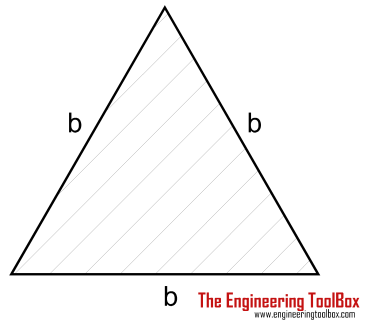 | Triangle Shaft | (1 / 20) τmax b3 | b = length of triangle side |
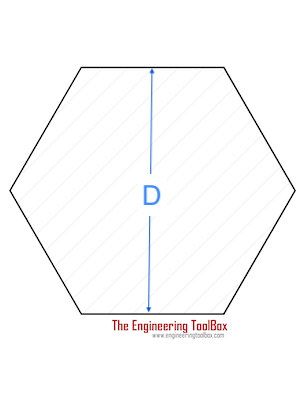 | Hexagon Shaft | 0.123 τmax D3 |
|
UNIT 8
TORSIONAL MOTION
Torsion of circular shafts
Definition of Torsion: Consider a shaft rigidly clamped at one end and twisted at the other end by a torque T = F.d applied in a plane perpendicular to the axis of the bar such a shaft is said to be in torsion.
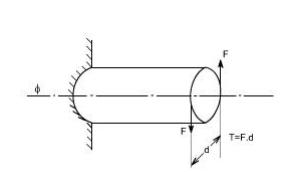
Effects of Torsion: The effects of a torsional load applied to a bar are
(i) To impart an angular displacement of one end cross section with respect to the other end.
(ii) To setup shear stresses on any cross section of the bar perpendicular to its axis.
GENERATION OF SHEAR STRESSES
The physical understanding of the phenomena of setting up of shear stresses in a shaft subjected to a torsion may be understood from the figure.
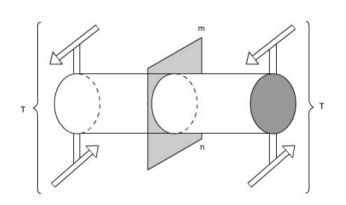
Fig: Here the cylindrical member or a shaft is in static equilibrium where T is the resultant external torque acting on the member. Let the member be imagined to be cut by some imaginary plane mn'.
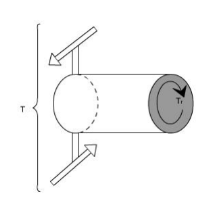
Fig 2: When the plane mn' cuts remove the portion on R.H.S. And we get a fig 2. Now since the entire member is in equilibrium, therefore, each portion must be in equilibrium. Thus, the member is in equilibrium under the action of resultant external torque T and developed resisting Torque Tr
.
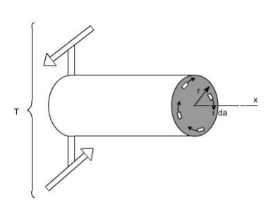
Fig 3: The Figure shows that how the resisting torque Tr is developed. The resisting torque Tr is produced by virtue of an infinites mal shear forces acting on the plane perpendicular to the axis of the shaft. Obviously such shear forces would be developed by virtue of sheer stresses.
Therefore we can say that when a particular member (say shaft in this case) is subjected to a torque, the result would be that on any element there will be shear stresses acting. While on other faces the complementary sheer forces come into picture. Thus, we can say that when a member is subjected to torque, an element of this member will be subjected to a state of pure shear.
Shaft: The shafts are the machine elements which are used to transmit power in machines.
Twisting Moment: The twisting moment for any section along the bar / shaft is defined to be the
Algebraic sum of the moments of the applied couples that lie to one side of the section under consideration. The choice of the side in any case is of course arbitrary.
Shearing Strain: If a generator a b is marked on the surface of the unloaded bar, then after the twisting moment 'T' has been applied this line moves to ab'. The angle measured in radians, between the final and original positions of the generators is defined as the shearing strain at the surface of the bar or shaft. The same definition will hold at any interior point of the bar.
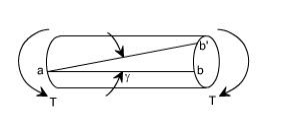
Modulus of Elasticity in shear: The ratio of the shear stress to the shear strain is called the modulus of elasticity in shear OR Modulus of Rigidity and in represented by the symbol
Angle of Twist: If a shaft of length L is subjected to a constant twisting moment T along its length, than the angle through which one end of the bar will twist relative to the other is known is the angle of twist.
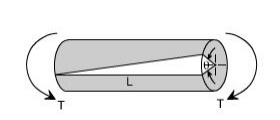
Despite the differences in the forms of loading, we see that there are number of similarities between bending and torsion, including for example, a linear variation of stresses and strain with position.
In torsion the members are subjected to moments (couples) in planes normal to their axes.
For the purpose of designing a circular shaft to withstand a given torque, we must develop an equation giving the relation between twisting moment, maximum shear stress produced, and a quantity representing the size and shape of the cross-sectional area of the shaft.
Not all torsion problems, involve rotating machinery, however, for example some types of
Vehicle suspension system employ torsional springs. Indeed, even coil springs are really curved members in torsion as shown in figure.
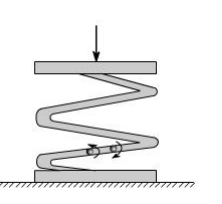
Many torque carrying engineering members are cylindrical in shape. Examples are drive shafts, bolts and screw drivers.
Torsion equation or torsion constant is defined as the geometrical property of a bar’s cross-section that is involved in the axis of the bar that has a relationship between the angle of twist and applied torque whose SI unit is m4. The torsion equation is given as follows:
T/J= τ/r=GΘ/L
Torsion equation derivation
Following are the assumptions made for the derivation of torsion equation:
- The material is homogeneous (elastic property throughout)
- The material should follow Hook’s law
- The material should have shear stress proportional to shear strain
- The cross-sectional area should be plane
- The circular section should be circular
- Every diameter of the material should rotate through the same angle
- The stress of the material should not exceed the elastic limit
Consider a solid circular shaft with radius R that is subjected to a torque T at one end and the other end under the same torque.
T = Maximum twisting torque or twisting moment
D = Diameter of shaft
R = Radius of shaft
J = Polar moment of Inertia
τ= Maximum Permissible Shear stress (Fixed for given material)
G = Modulus of rigidity
θ= Angle of twist (Radians) = angle D'OD L = Length of shaft.
?= Angle D'CD = Angle of Shear strain
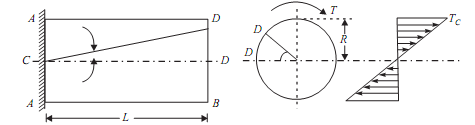
Than Torsion equation is: T/J = τ/R = G. θ /L
Let the shaft is subjected to a torque or twisting moment 'T'. And hence every C.S. Of this shaft will be subjected to shear stress.
Now distortion at the outer surface = DD'
Shear strain at outer surface = Distortion/Unit length tan? = DD'/CD
i.e. shear stress at the outer surface (tan? ) = DD'/L or = DD'/L ...(i)
Now DD' = R.θ or ?= R .θ /L ...(ii)
Now G = Shear stress induced/shear strain produced
G = τ / (R. θ /L);
Or; τ/R = G. θ /L …..(A);
This equation is called Stiffness equation.
Hear G, θ , L are constant for a given torque 'T'. That is proportional to R
If τ r be the intensity of shear stress at any layer at a distance 'r' from canter of the shaft, then;

Now from equation (ii) T = (τ/R) J
Or τ/R = T/J; ..(B)
This equation is called as strength equation
The combined equation A and B; we get
T/J = τ/R = G. θ /L
This equation is called as Torsion equation.
From the relation T/J = τ/R We have T = τ .J/R = τ .ZP
For the given shaft IP and R are constants and IP/R is thus constant and is called as POLAR MODULUS(ZP). Of the shaft section.
Polar modulus of section is thus measure of strength of shaft in the torsion.
TORSIONAL RIGIDITY or Torsional Stiffness (K): = G.J/L = T/θ
Deformation of a Circular Bar
Consider a bar or shaft of circular cross section twisted by a couple T, assume the left-hand end is fixed and the right-hand end will rotate a small angle ϕ, called angle of twist if every cross section has the same radius and subjected to the same torque, the angle ϕ (x) will vary linearly between ends under twisting deformation, it is assumed
1. Plane section remains plane
2. Radii remaining straight and the cross sections remaining plane and circular
3. If ϕ is small, neither the length L nor its radius will change consider an element of the bar dx, on its outer surface we choose an small element abcd,
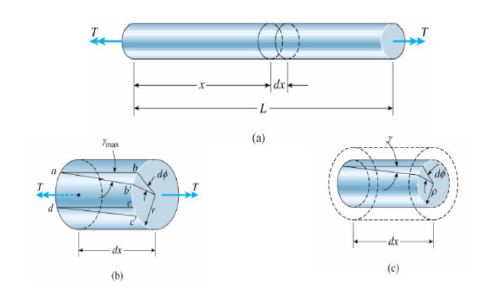
During twisting the element rotate a small angle d, the element is in
a state of pure shear, and deformed into ab'c'd, its shear strain γmax is
γmax = bb’/ab = r d ϕ / dx
d ϕ / dx represents the rate of change of the angle of twist ϕ, denote θ= d ϕ / dx as the angle of twist per unit length or the rate of twist, then γmax = r θ in general, ϕ and θ are function of x, in the special case of pure torsion, θ is constant along the length (every cross section is subjected to the same torque) θ = ϕ/L and γmax = rθ/L and the shear strain inside the bar can be obtained
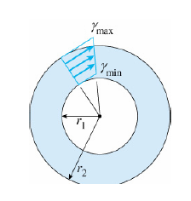
γ = ρ.θ=ρ. γmax / r
γmin = r1 /r2 γmax
For a circular tube, it can be obtained .the above relationships are based only upon geometric concepts, they are valid for a circular bar of any material, elastic or inelastic, linear or nonlinear.
Torsion or twisting moment
A shaft will said to be in torsion, if it will be subjected with two equal and opposite torques applied at its two ends. When a shaft will be subjected to torsion or twisting moment, there will be developed shear stress and shear strain in the shaft material.
We will discuss here one case of a hollow circular shaft which will be subjected to torsion and we will secure here the expression for maximum torque transmitted by a hollow circular shaft.
We have following information from above figure
Ro = Outer radius of the hollow circular shaft
Ri = Inner radius of the hollow circular shaft
Do = Outer diameter of the hollow circular shaft
Di = Inner diameter of the hollow circular shaft
Dr = Thickness of small elementary circular ring
r = Radius of the small elementary of circular ring
q = Shear stress at a radius r from the centre of the hollow circular shaft
τ = Maximum shear stress at outer surface of shaft
DA = Area of the small elementary of circular ring
DA = 2П x r x dr
Shear stress, at a radius r from the centre, could be determined as mentioned here
q/ r = τ / Ro
q = τ x r/ Ro
Turning force due to shear stress at a radius r from the centre could be determined as mentioned here
DF = q x dA
DF = τ x r/ Ro x 2П x r x dr
DF = τ/ Ro x 2П r2dr
Twisting moment at the circular elementary ring could be determined as mentioned here
DT = Turning force x r
DT = τ/ Ro x 2П r3dr
Total torque could be easily determined by integrating the above equation between limits Ri and Ro.
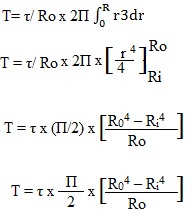
Therefore total torque transmitted by a hollow circular shaft will be given by following formula
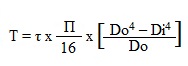
Circular Shaft and Maximum Moment or Torque
Maximum moment in a circular shaft can be expressed as:
Tmax = τmax J / R (1)
Where
Tmax = maximum twisting torque (Nm, lbf ft)
τmax = maximum shear stress (Pa, lbf/ft2)
R = radius of shaft (m, ft)
Combining (2) and (3) for a solid shaft
Tmax = (π / 16) τmax D3 (1b)
Combining (2) and (3b) for a hollow shaft
Tmax = (π / 16) τmax (D4 - d4) / D (1c)
Circular Shaft and Polar Moment of Inertia
Polar Moment of Inertia of a circular solid shaft can be expressed as
J = π R4 / 2
= π (D / 2)4 / 2
= π D4 / 32 (2)
Where
D = shaft outside diameter (m, in)
Polar Moment of Inertia of a circular hollow shaft can be expressed as
J = π (D4 - d4) / 32 (2b)
Where
d = shaft inside diameter (m, ft)
Diameter of a Solid Shaft
Diameter of a solid shaft can calculated by the formula
D = 1.72 (Tmax / τmax)1/3 (3)
Torsional Deflection of Shaft
The angular deflection of a torsion shaft can be expressed as
α = L T / (J G) (4)
Where
α = angular shaft deflection (radians)
L = length of shaft (m, ft)
G = Shear Modulus of Rigidity - or Modulus of Rigidity (Pa, psf)
The angular deflection of a torsion solid shaft can be expressed as
α = 32 L T / (G π D4) (4a)
The angular deflection of a torsion hollow shaft can be expressed as
α = 32 L T / (G π (D4- d4)) (4b)
The angle in degrees can be achieved by multiplying the angle θ in radians with 180 / π.
Solid shaft (π replaced)
αdegrees ≈ 584 L T / (G D4) (5a)
Hollow shaft (π replaced)
αdegrees ≈ 584 L T / (G (D4- d4) (5b)
Shaft Cross Section Area | Maximum Torsional | Nomenclature | |
 | Solid Cylinder Shaft | (π / 16) τmax (2 r)3 = (π / 16) τmax D3 |
|
 | Hollow Cylinder Shaft | (π / 16) τmax ((2 R)4 - (2 r)4) / (2 R) = (π / 16) τmax (D4 - d4) / D |
|
 | Ellipse Shaft | (π / 16) τmax b2 h | h = "height" of shaft |
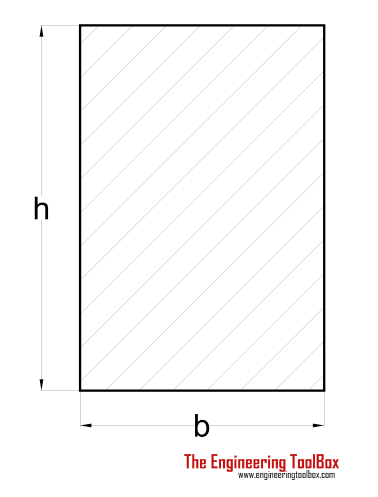 | Rectangle Shaft | (2 / 9) τmax b2 h | h > b |
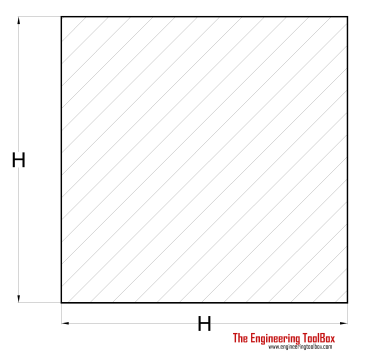 | Square Shaft | (2 / 9) τmax H3 |
|
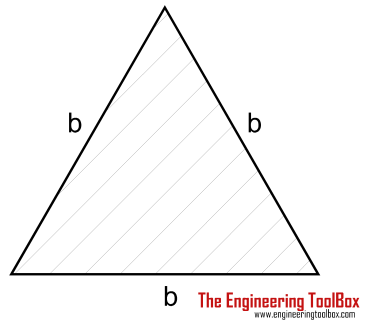 | Triangle Shaft | (1 / 20) τmax b3 | b = length of triangle side |
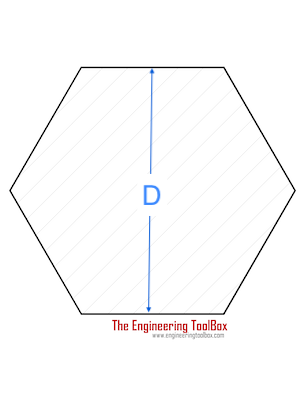 | Hexagon Shaft | 0.123 τmax D3 |
|