Unit - 6
Ordinary differential equations of higher order
Linear differential equation is those in which the independent variable and its derivative occur only in the first degree and are not multiplied together.
Thus, the general linear differential equation of the n’th order is of the form
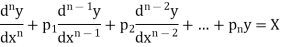
Where 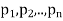 and X are function of x.
and X are function of x.
Linear differential equation with constant co-efficient are of the form-
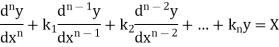
where 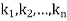 are constants.
are constants.
Rules to find the complementary function-
To solve the equation-
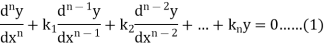
This can be written as in symbolic form-
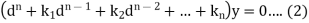
Or-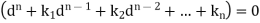
It is called the auxiliary equation.
Let 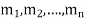 be the roots-
be the roots-
Case-1: If all the roots are real and distinct, then equation (2) becomes,
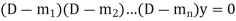
Now this equation will be satisfied by the solution of 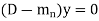
This is a Leibnitz’s linear and I.F. = 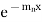
Its solution is-
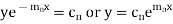
The complete solution will be-
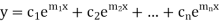
Case-2: If two roots are equal 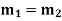
Then complete solution is given by-
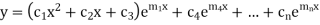
Case-3: If one pair of roots be imaginary, i.e., 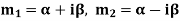 then the complete solution is-
then the complete solution is-
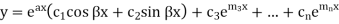
Where 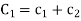 and
and 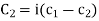
Case-4: If two points of imaginary roots be equal-
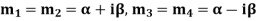
Then the complete solution is-
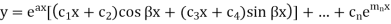
Example-Solve 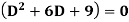
Sol.
Its auxiliary equation is-
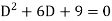
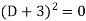
Where-
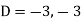
Therefore, the complete solution is-
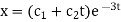
Inverse operator-
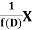 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
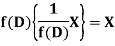
So that 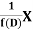 satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 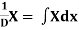
2. 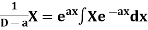
Rules for finding the particular integral-
Let us consider the equation-
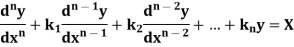
Or in symbolic form-
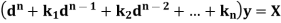
So that-
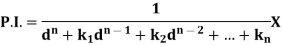
Now-
Case-1: When X = 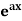
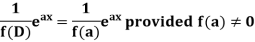
In case f(a) = 0, then we see that the above rule will not work,
So that-
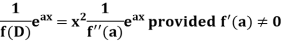
Example: Find the P.I. of (D + 2)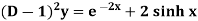
Sol.
P.I. = 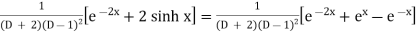
Now we will evaluate each term separately-
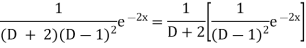
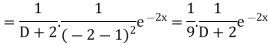
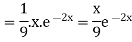
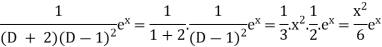
And
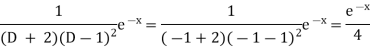
Therefore-
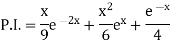
Example: Solve (D – D’ – 2) (D – D’ – 3) z = 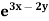
Sol.
The C.F. will be given by-
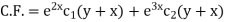
Particular integral-
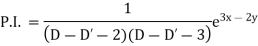
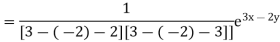
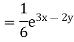
Therefore, the complete solution is-
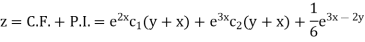
Case-2: when X = sin (ax + b) or cos (ax + b)
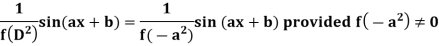
In case 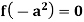 then the above rule fails.
then the above rule fails.
Now-
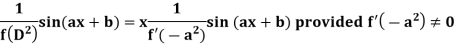
And if 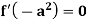
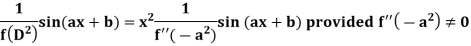
Similarly-
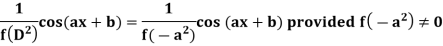
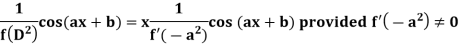
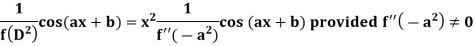
Example: Find the P.I. of 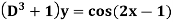
Sol.
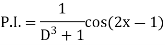

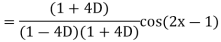
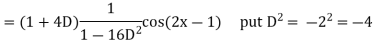
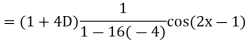
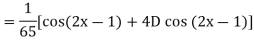
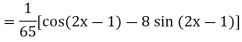
Example: Find the P.I. of (D + 1) (D + D’ – 1) z = sin (x + 2y)
Sol.
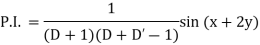
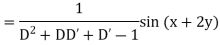
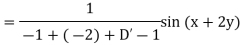
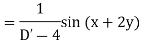
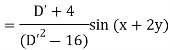
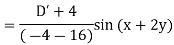
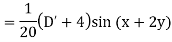
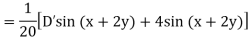
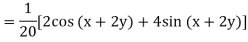
Example: Find P.I. of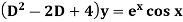
Sol. P.I = 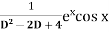
Replace D by D+1
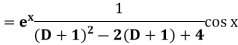
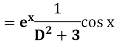
Put 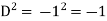
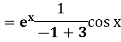
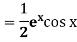
Method of variation of parameters-
Consider a second order LDE with constant co-efficient given by
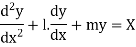
Then let the complimentary function 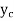 is given by
is given by
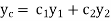
Then the particular integral is
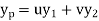
Where u and v are unknown and to be calculated using the formula
u=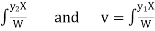
Example-1: Solve the following DE by using variation of parameters-
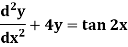
Sol. We can write the given equation in symbolic form as-
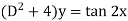
To find CF-
It’s A.E. is 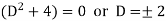
So that CF is- 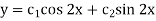
To find PI-
Here 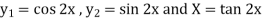
Now 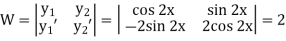
Thus PI = 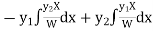
= 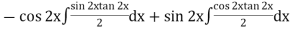
= 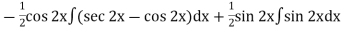
= 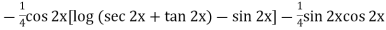
= 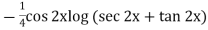
So that the complete solution is-
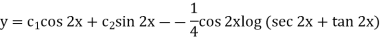
Example-2: Solve the following by using the method of variation of parameters.
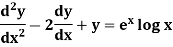
Sol. This can be written as-
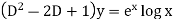
C.F.-
Auxiliary equation is- 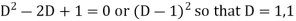
So that the C.F. will be- 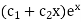
P.I.-
Here 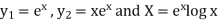
Now 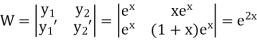
Thus PI = 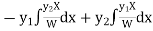
= 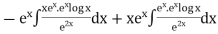
= 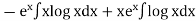
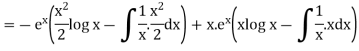
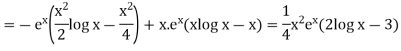
So that the complete solution is-
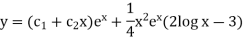
An equation of the form
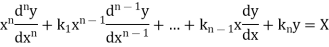
Here X is the function of x, is called Cauchy’s homogeneous linear equation.
Example-1: Solve 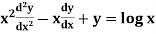
Sol. As it is a Cauchy’s homogeneous linear equation.
Put 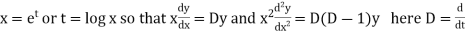
Then the equation becomes [D(D-1)-D+1] y = t or 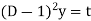
Auxiliary equation-
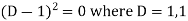
So that-
C.F.=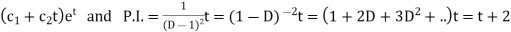
Hence the solution is- 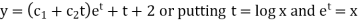 , we get-
, we get-
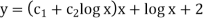
Example-2: Solve 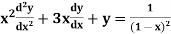
Sol. On putting 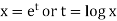 so that,
so that,
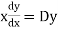 and
and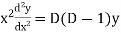
The given equation becomes-
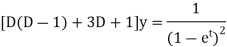
Or it can be written as-
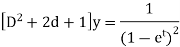
So that the auxiliary equation is- 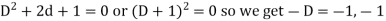
C.F. = 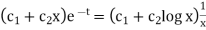
Particular integral- 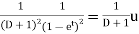
Where 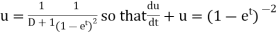
It’s a Leibnitz’s linear equation having I.F.=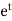
Its solution will be-
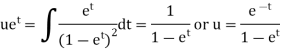
P.I. = 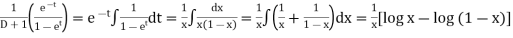
= 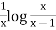
So that the complete solution is-
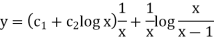
An equation of the form-
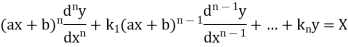
is called Legendre’s linear equation.
Example-3: Solve 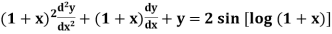
Sol. As we see that this is a Legendre’s linear equation.
Now put 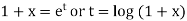
So that- 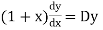
And 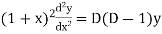
Then the equation becomes- D (D – 1) y+ Dy + y = 2 sin t
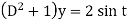
Its auxiliary equation is- 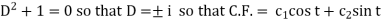
And particular integral-
P.I. = 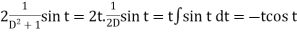
Note - 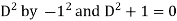
Hence the solution is - 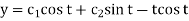
We know that the solution of the differential equation-
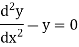
Are
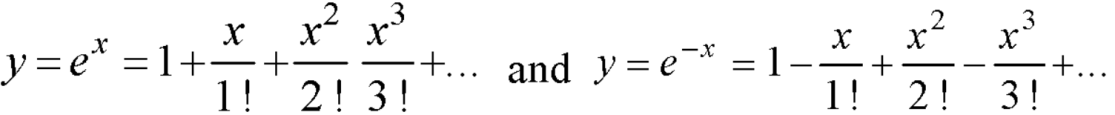
These are the power series solutions of the given differential equations.
Ordinary Point-
Let us consider the equation-
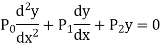
Here 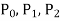 are polynomial in x.
are polynomial in x.
X = a is an ordinary point of the above equation if 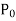 does not vanish for x = a.
does not vanish for x = a.
Note- If 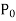 vanishes for x = a, then x = a is a singular point.
vanishes for x = a, then x = a is a singular point.
Solution of the differential equation when x = 0 is an ordinary point, which means 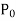 does not vanish for x = 0.
does not vanish for x = 0.
1. Let 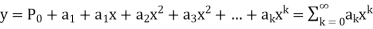 be the solution of the given differential equation.
be the solution of the given differential equation.
2. Find 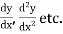
3.
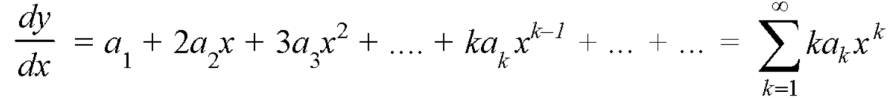
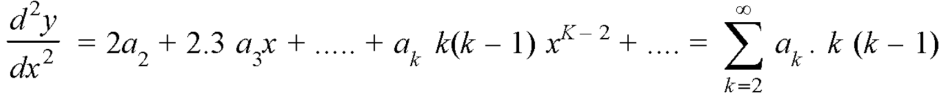
4. Substitute the expressions of y, 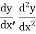 etc. in the given differential equations.
etc. in the given differential equations.
5. Calculate 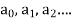 Coefficients of various powers of x by equating the coefficient to zero.
Coefficients of various powers of x by equating the coefficient to zero.
6. Put the values of 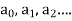 In the differential equation to get the required series solution.
In the differential equation to get the required series solution.
Example- Solve
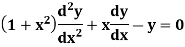
Sol.
Here we have-
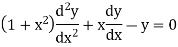
Let the solution of the given differential equation be-
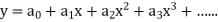
Since x = 0 is the ordinary point of the given equation-
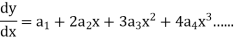
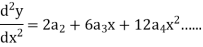
Put these values in the given differential equation-
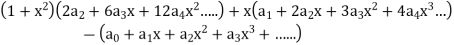
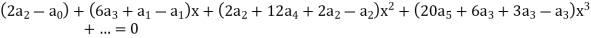
Equating the coefficients of various powers of x to zero, we get-
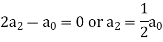
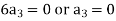
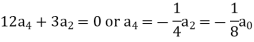
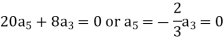
Therefore, the solution is-
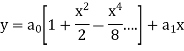
Example: Solve in series the equation-
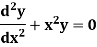
Sol.
Here we have-
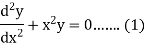
Let us suppose-
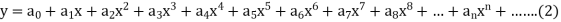
Since x = 0 is the ordinary point of (1)-
Then-
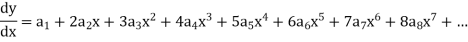
And
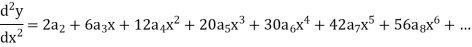
Put these values in equation (1)-
We get-
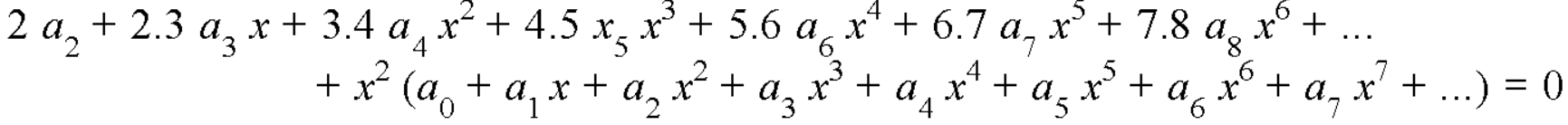
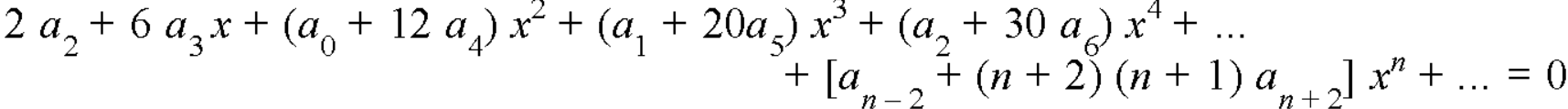
Equating to zero the coefficients of the various powers of x, we get-
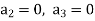
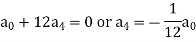
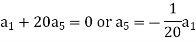
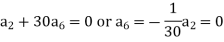
And so on….
In general, we can write-
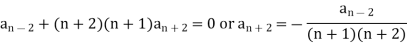
Now putting n = 5,
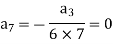
Put n = 6-
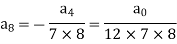
Put n = 7,
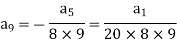
Put n = 8,
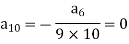
Put n = 9,
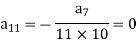
Put n = 10,
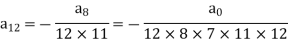
Put the above values in equation (1), we get-
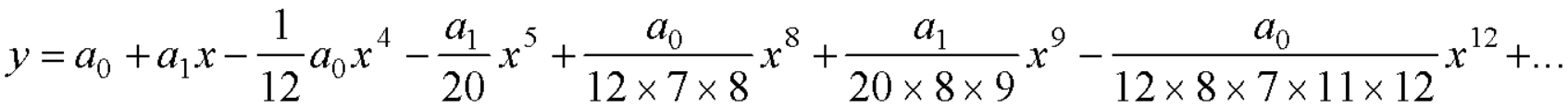
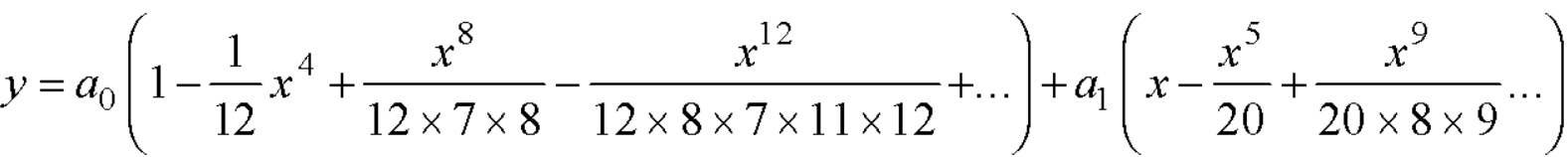
The Legendre’s equation is-
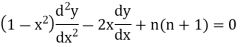
Now the solution of the given equation is the series of descending powers of x is-
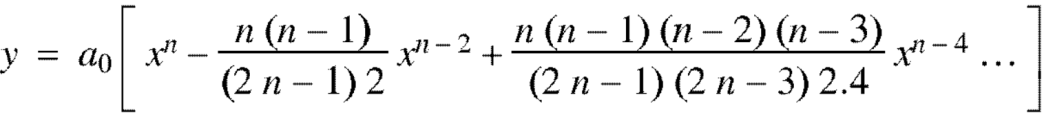
Here 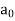 is an arbitrary constant.
is an arbitrary constant.
If n is a positive integer and
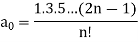
The above solution is 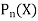
So that-
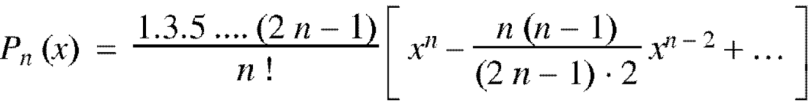
Here 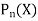 is called the Legendre’s function of first kind.
is called the Legendre’s function of first kind.
Note- Legendre’s equations of second kind is 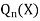 and can be defined as-
and can be defined as-
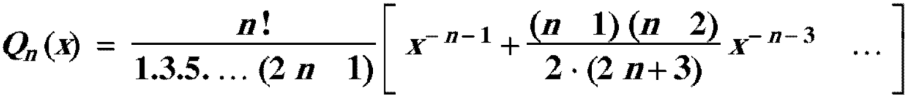
The general solution of Legendre’s equation is-
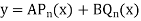
Here A and B are arbitrary constants.
Rodrigue’s formula-
Rodrigue’s formula can be defined as-
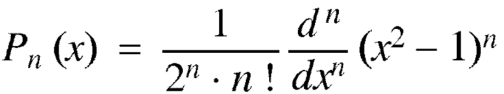
Legendre Polynomials-
We know that by Rodrigue formula-
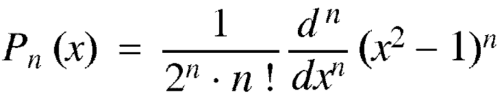
If n = 0, then it becomes-
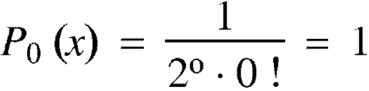
If n = 1,
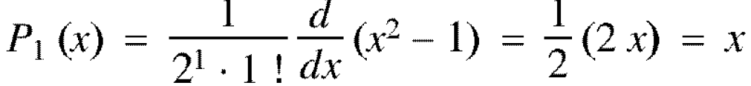
If n = 2,
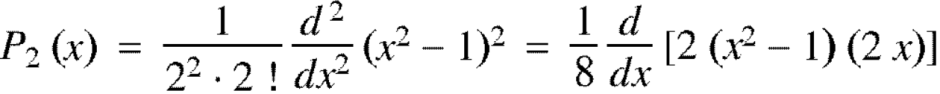
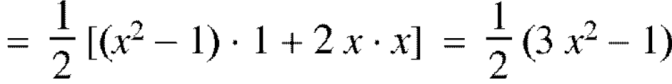
Now putting n =3, 4, 5……...n we get-
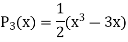
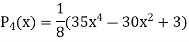
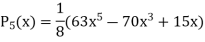
…………………………………..
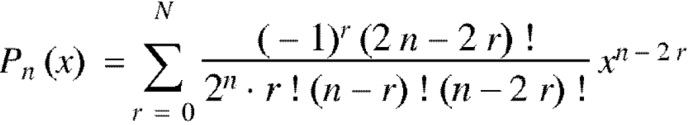
Where N = n/2 if n is even and N = 1/2 (n-1) if n is odd.
Example: Express 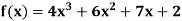 in terms of Legendre polynomials.
in terms of Legendre polynomials.
Sol.
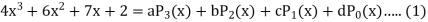
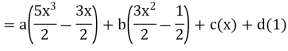
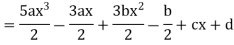
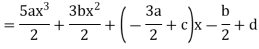
By equating the coefficients of like powers of x, we get-
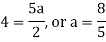
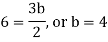
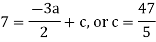
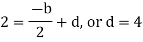
Put these values in equation (1), we get-
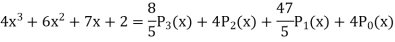
Example: Let 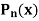 be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-
be the Legendre’s polynomial of degree n, then show that for every function f(x) for which the n’th derivative is continuous-
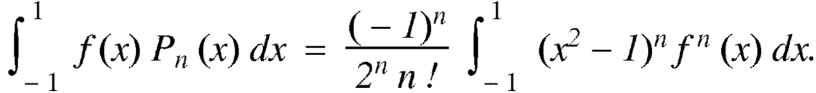
Sol.
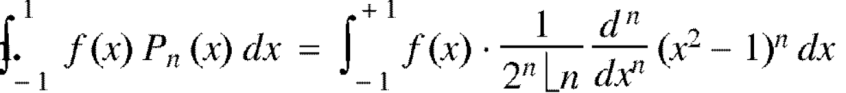
We know that-
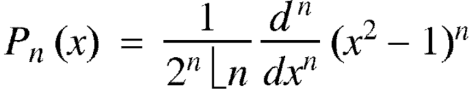
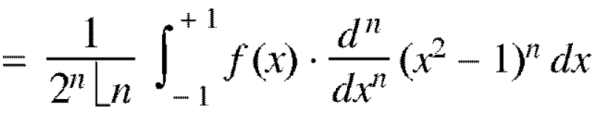
On integrating by parts, we get-
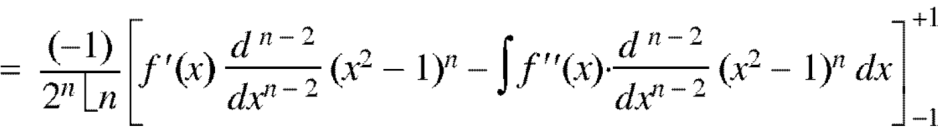
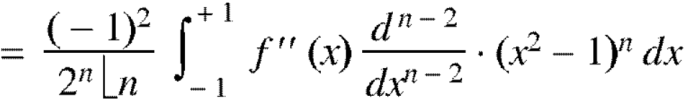
Now integrate (n – 2) times by parts, we get-
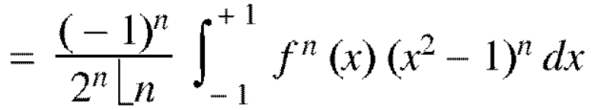
Recurrence formulae for 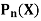 -
-
Formula-1:
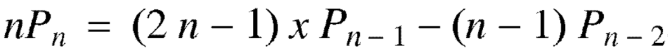
Fromula-2:
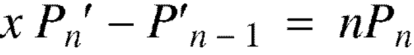
Formula-3:
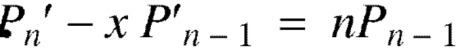
Formula-4:
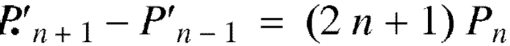
Formula-5:
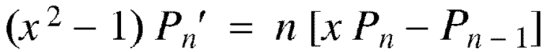
Formula-6:
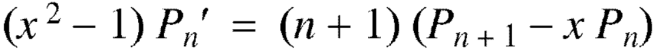
Generating function for 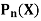
Prove that 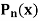 is the coefficient of
is the coefficient of 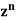 in the expansion of
in the expansion of 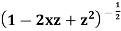 in ascending powers of z.
in ascending powers of z.
Proof:
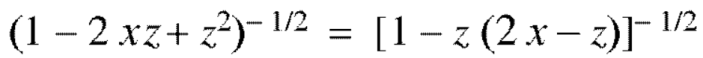
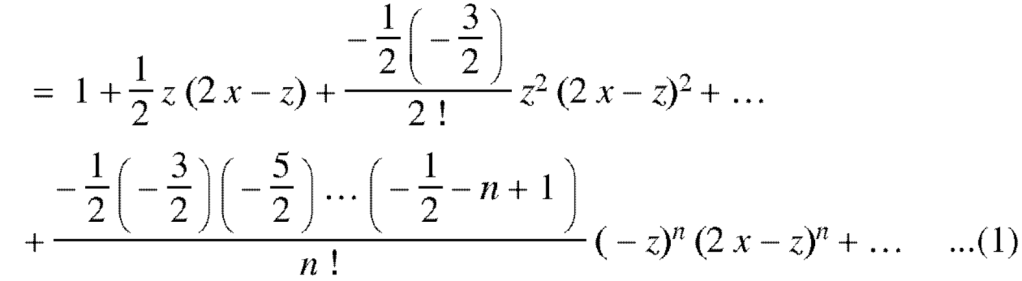
Now coefficient of 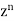 in
in
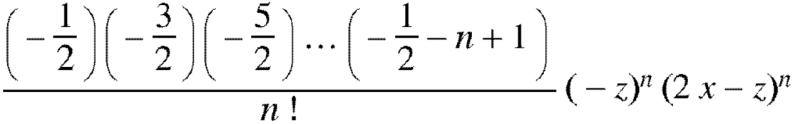
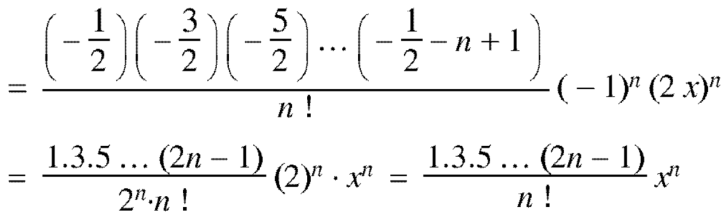
Coefficient of 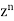 in
in
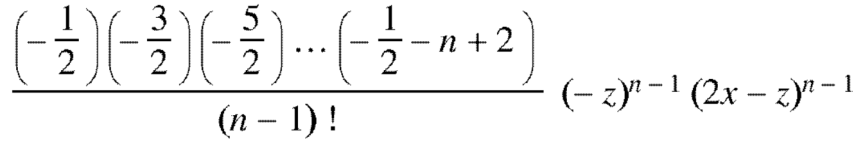
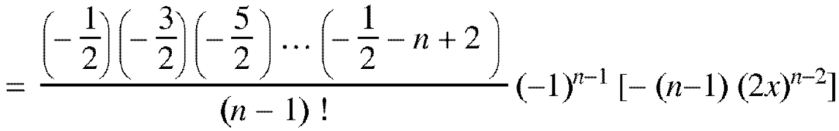
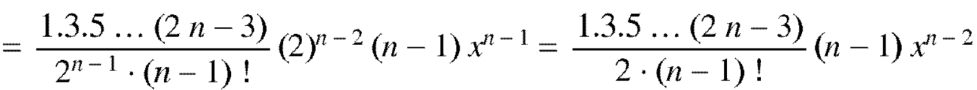
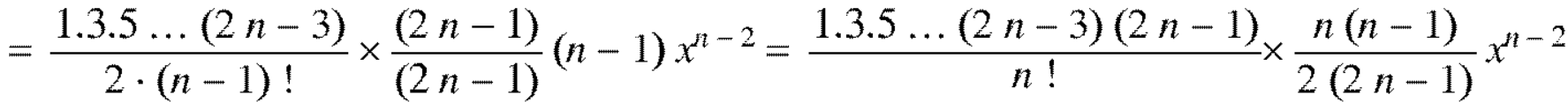
Coefficient of 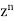 in
in
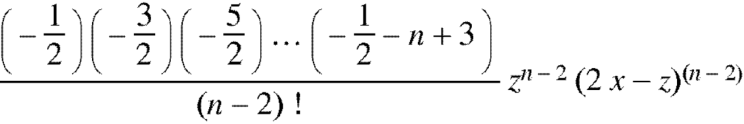
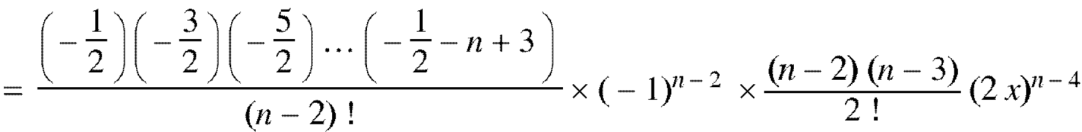
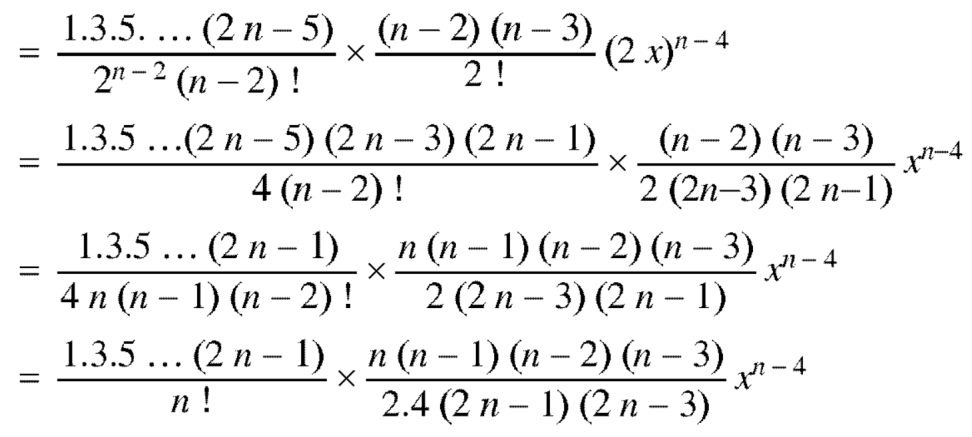
And so on.
Coefficient of 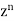 in the expansion of equation (1)-
in the expansion of equation (1)-
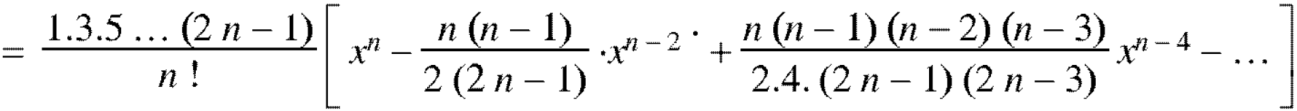
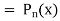
The coefficients of 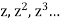 etc. in (1) are
etc. in (1) are 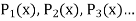
Therefore-
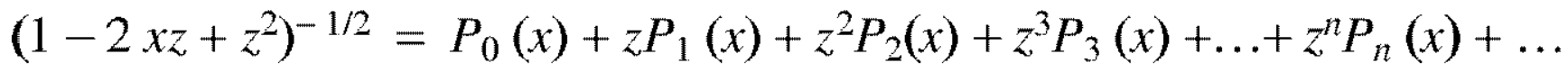
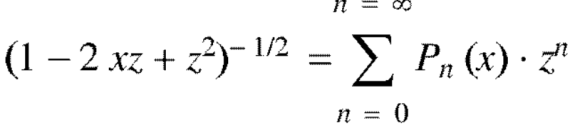
Example: Show that-
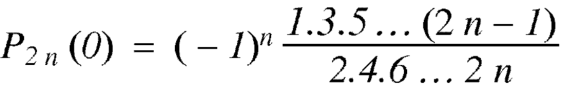
Sol.
We know that
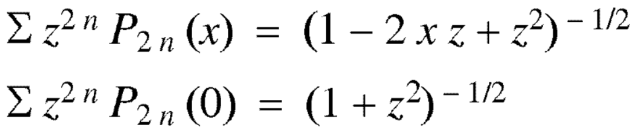
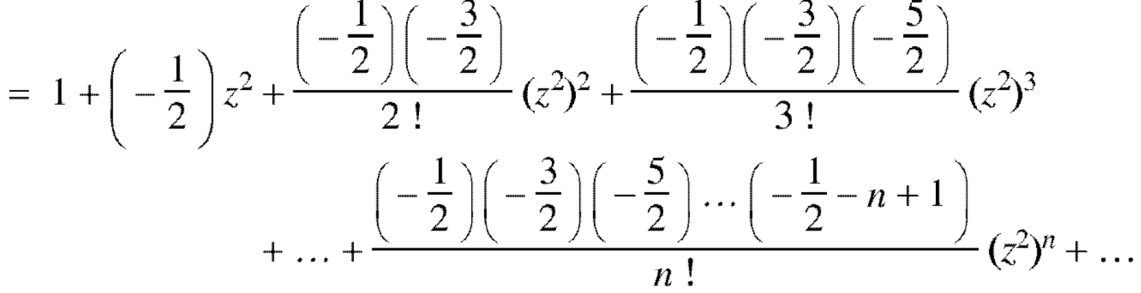
Equating the coefficients of 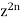 both sides, we have-
both sides, we have-
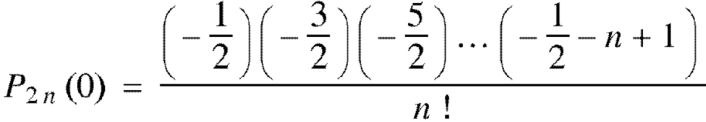
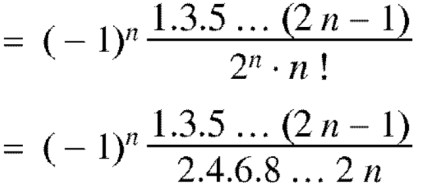
Orthogonality of Legendre polynomials
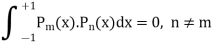
Proof:  is a solution of
is a solution of
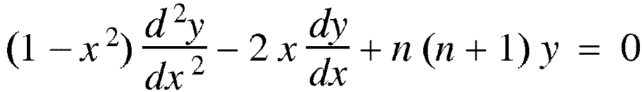 …………………. (1)
…………………. (1)
And
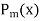 is a solution of-
is a solution of-
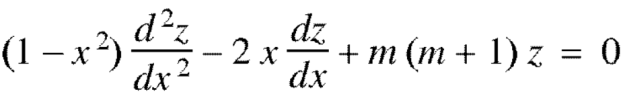 ……………. (2)
……………. (2)
Now multiply (1) by z and (2) by y and subtracting, we have-
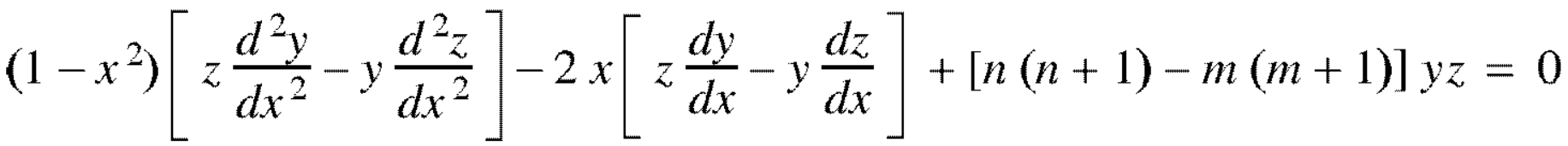

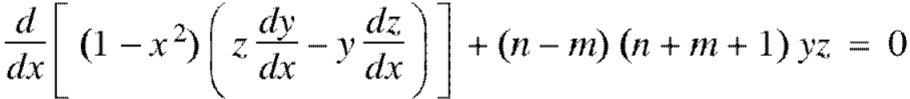
Now integrate from -1 to +1, we get-
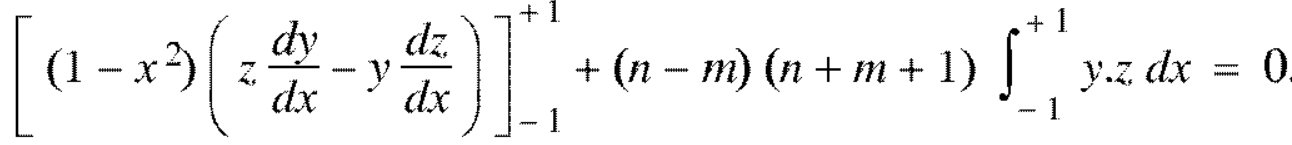
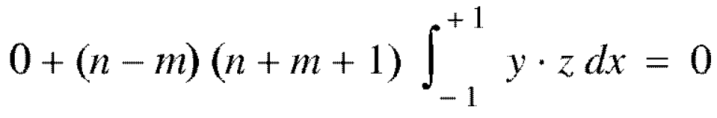
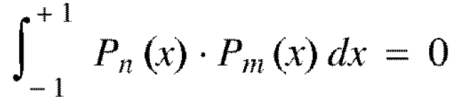
Example: Prove that-

By using Rodrigue formula for Legendre function.
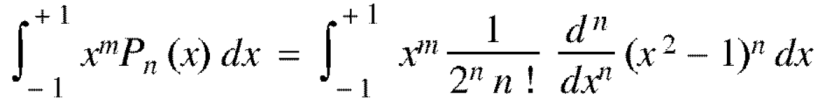
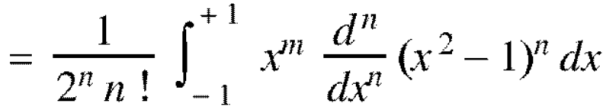
On integrating by parts, we get-
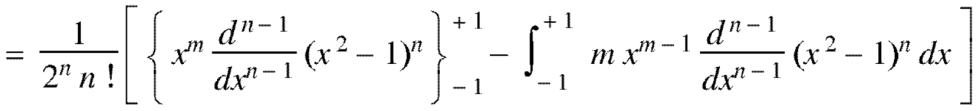
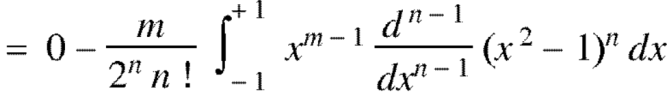
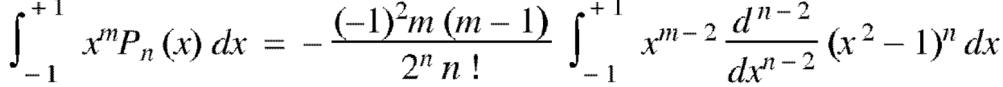
Now integrating m – 2 times, we get-
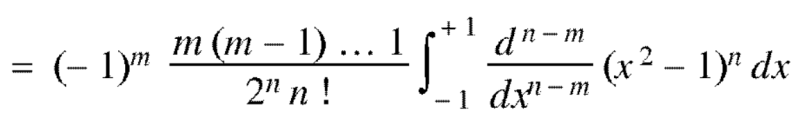
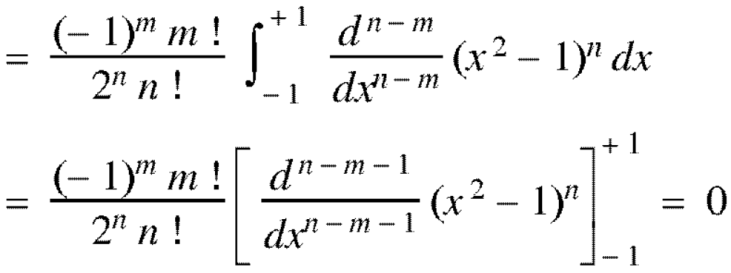
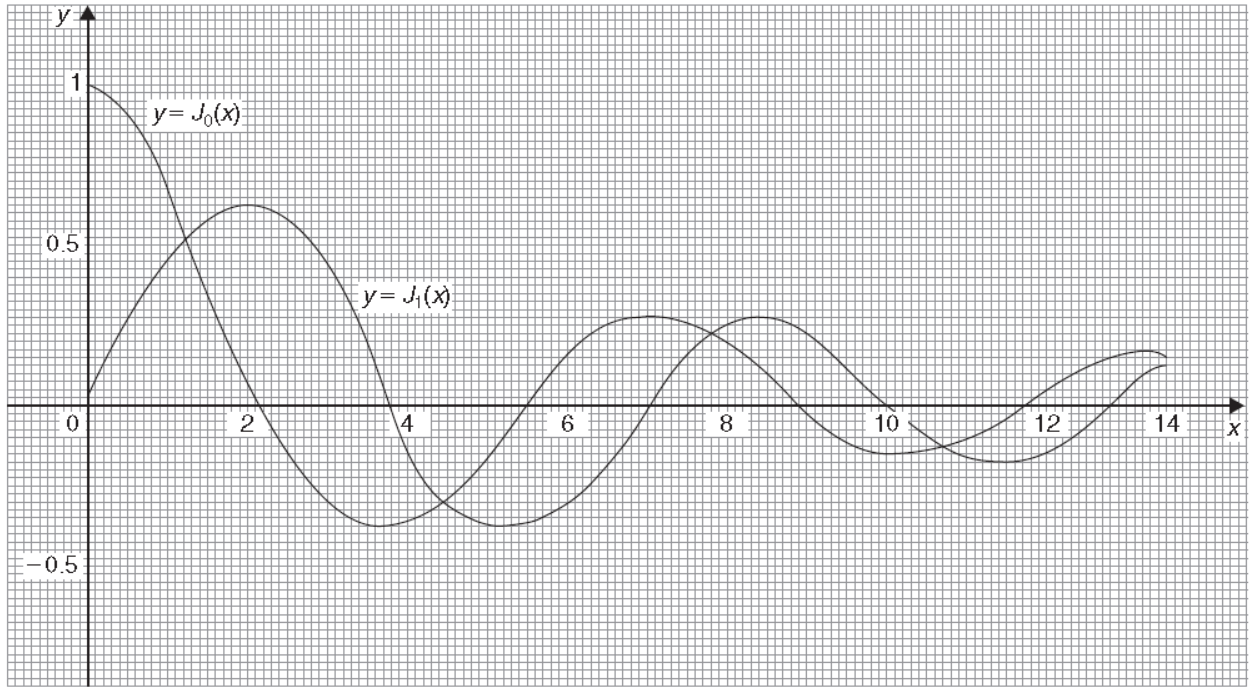
The Bessel equation is-
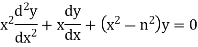
The solution of this equations will be-
The Bessel function is denoted by 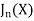 and defined as-
and defined as-
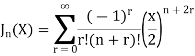
If we put n = 0 then Bessel function becomes-
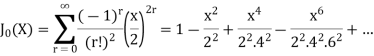
Now if n = 1, then-
The graph of these two equations will be-
General solution of Bessel equation-
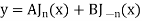
Example: Prove that-
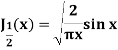
Sol.
As we know that-
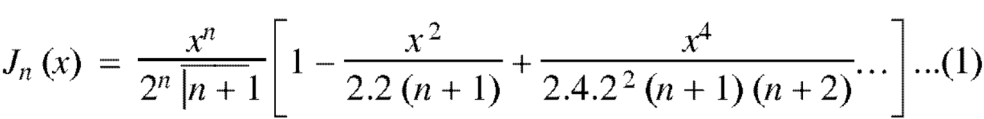
Now put n = 1/2 in equation (1), then we get-
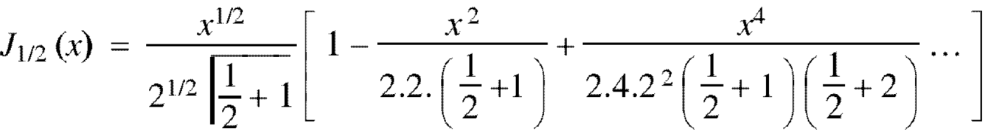
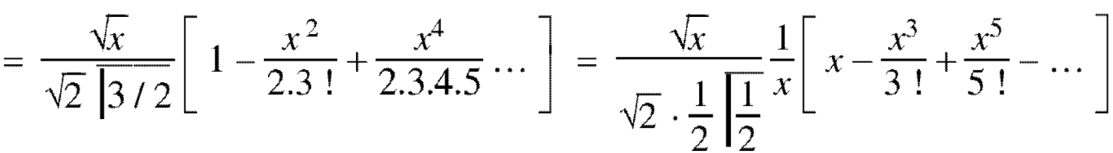
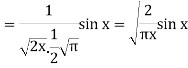
Hence proved.
Example: Prove that-
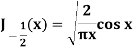
Sol.
Put n = -1/2 in equation (1) of the above question, we get-
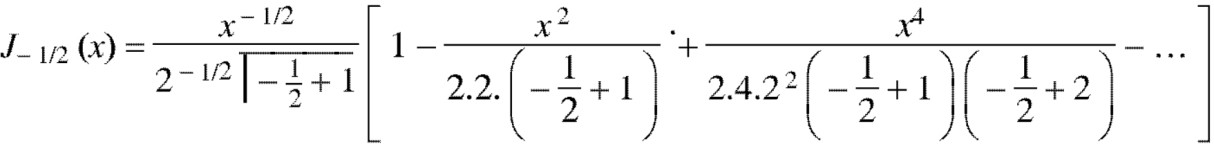
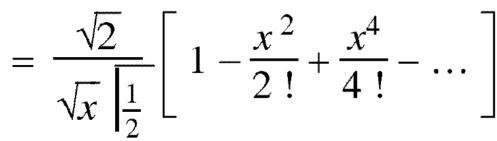
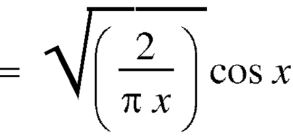
Recurrence formulae –
Formula-1: 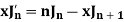
Proof:
As we know that-
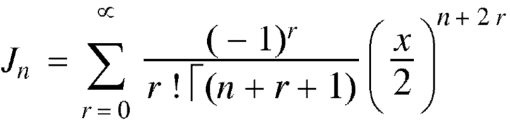
On differentiating with respect to x, we obtain-
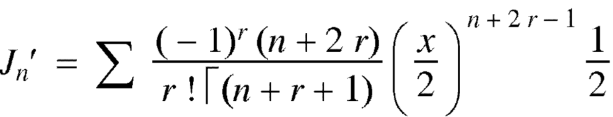
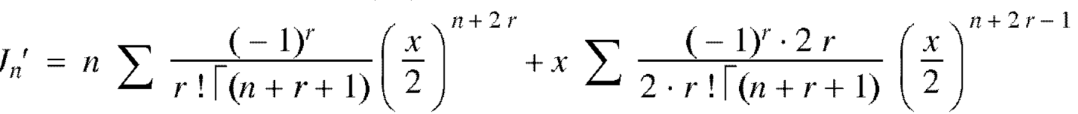
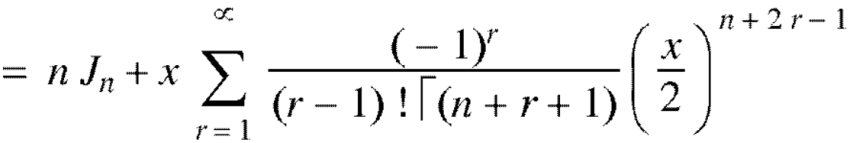
Putting r – 1 = s
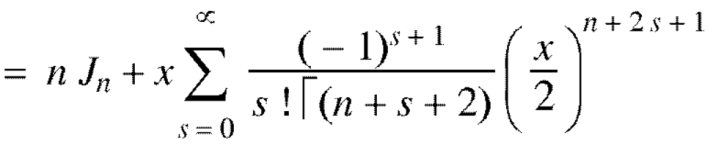
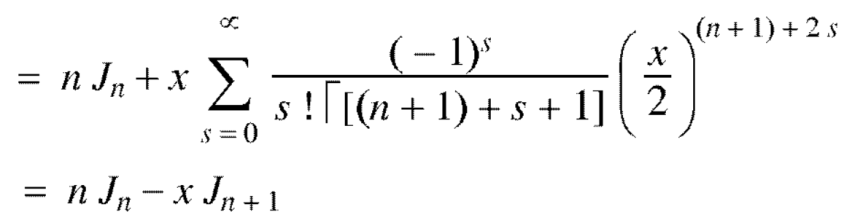
Formula-2: 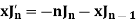
Proof:
We have-
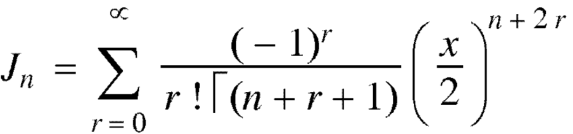
Differentiating w.r.t. x, we get-
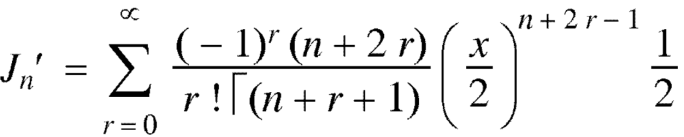
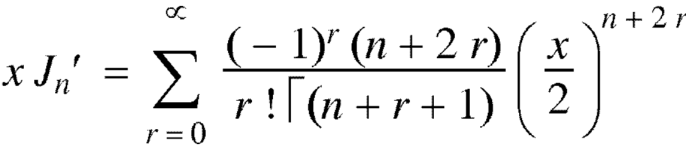
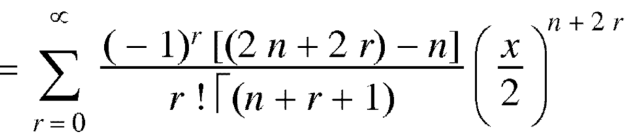
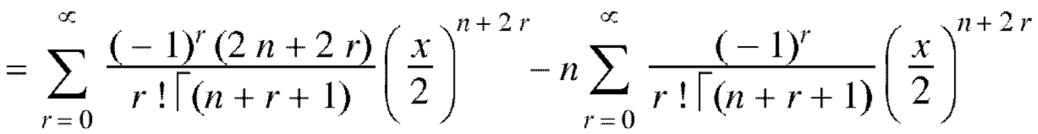
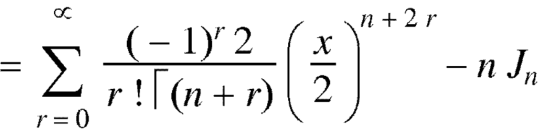
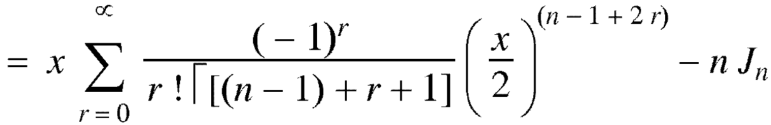
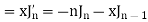
Formula-3: 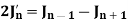
Proof: We know that from formula first and second-
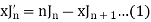
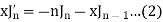
Now adding these two, we get-
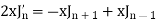
Or
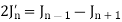
Formula-4: 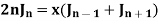
Proof:
We know that-
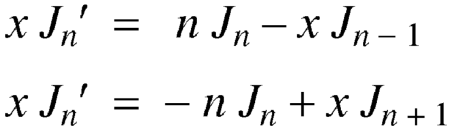
On subtracting, we get-
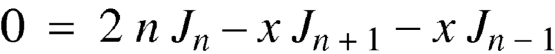
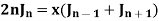
Formula-5: 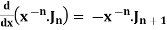
Proof:
We know that-
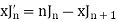
Multiply this by 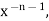 we get-
we get-
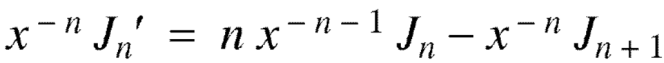
I.e.
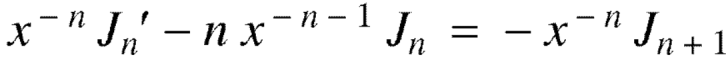
Or
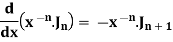
Formula-6: 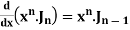
Proof:
We know that-
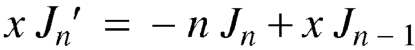
Multiply by 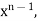 we get-
we get-
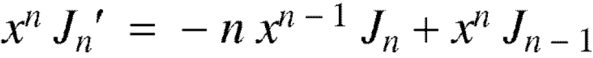
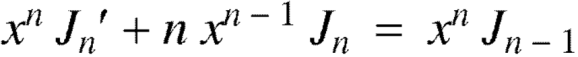
Or
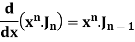
Example: Show that-
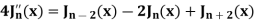
By using recurrence relation
Sol.
We know that-
The recurrence formula-
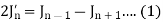
On differentiating, we get-
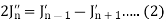
Now replace n by n -1 and n by n+1 in (1), we have-
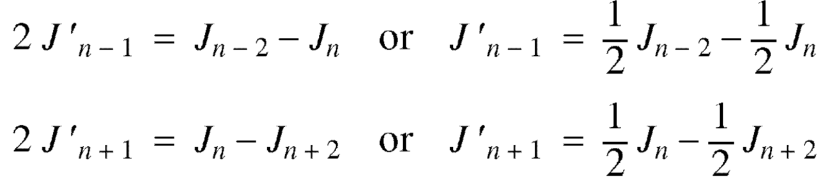
Put the values of 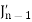 and
and 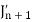 from the above equations in (2), we get-
from the above equations in (2), we get-
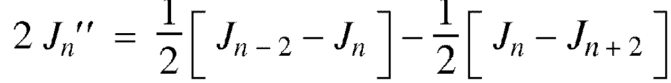
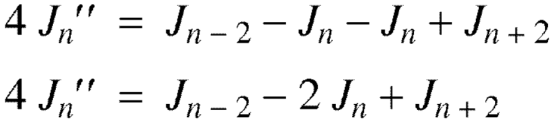
Example: Prove that-
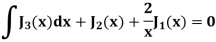
Sol.
We know that- from recurrence formula
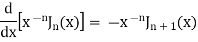
On integrating we get-
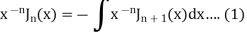
On taking n = 2 in (1), we get-
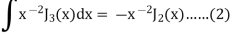
Again-
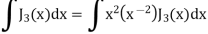
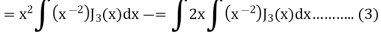
Put the value of 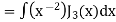 from equation (2) and (3), we get-
from equation (2) and (3), we get-
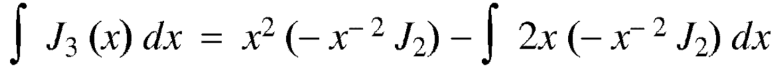
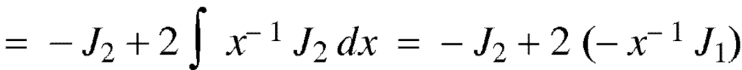
By equation (1), when n = 1
References:
1. G.B. Thomas and R.L. Finney, “Calculus and Analytic Geometry”, Pearson, 2002.
2. T. Veerarajan, “Engineering Mathematics”, McGraw-Hill, New Delhi, 2008.
3. B. V. Ramana, “Higher Engineering Mathematics”, McGraw Hill, New Delhi, 2010.
4. N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
5. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.