UNIT-4
Applied statistics (Module-5 contd.)-
Module-6
Small sample
5.1. Test of significance: Large sample test for single proportion
Large Sample Test for a Proportion
- The sampling distribution of
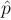 is approximately normal.
is approximately normal. - Use the value of p in the null hypothesis when computing the standard deviation of
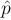 .
. - The test statistic is
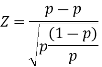
Hypothesis Test: Difference Between Proportions
This lesson describes how to conduct a hypothesis test to define whether the difference between two proportions is significant.
The test procedure, called the two-proportion z-test, is suitable when the following conditions are met:
- The sampling method for each population is simple random sample.
- The examples are independent.
- Each example comprises at least 10 attainments and 10 failures.
- Each population is at least 20 times as big as its example.
This approach contains of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.
Test Your Considerate
In this section, two sample difficulties illustrate how to conduct a hypothesis test for the difference between two sizes. The first problem includes two-tailed test; the second problem, a one-tailed test.
Problem 1: Two-Tailed Test
Suppose Acme Drug Company is making a new medicine designed to prevent colds. The company claims that the drug is equally effective for men and women. To test this claim, they chose a simple random sample of 100 women and 200 men from a population of 100,000 volunteers.
At the end of the study, 38% of the women had a cold; and 51% of men caught a cold. Based on these results, can we rule out the company's claim that the drug is equally effective for men and women? Use a significance level of 0.05.
Solution: The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results. We work through the following steps:
State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis.
Null hypothesis: P1 = P2
Alternative hypothesis: P1 ≠ P2
Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the proportion of population 1 is too large or too small.
Formulate an analysis plan. For this analysis, the significance level is 0.05. The test method is a two-sided z-test.
Analyze the sample data. Using the sample data, we calculated the proportion of the pooled sample (p) and the standard error (SE). Using these measures, we compute the z-score (z) test statistic.
p = (p1 * n1 + p2 * n2) / (n1 + n2)
p = [(0.38 * 100) + (0.51 * 200)] / (100 + 200)
p = 140/300 = 0.467
SE = sqrt{ p * ( 1 - p ) * [ (1/n1) + (1/n2) ] }
SE = sqrt[ 0.467 * 0.533 * ( 1/100 + 1/200 ) ]
SE = sqrt [0.003733] = 0.061
z = (p1 - p2) / SE = (0.38 - 0.51)/0.061 = -2.13
Suppose Acme Drug Company is making a new medicine designed to prevent colds. The company claims that the drug is equally effective for men and women. To test this claim, they chose a simple random sample of 100 women and 200 men from a population of 100,000 volunteers. At the end of the study, 38% of the women had a cold; and 51% of men caught a cold. Based on these results, can we rule out the company's claim that the drug is equally effective for men and women? Use a significance level of 0.05. Solution: The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results. We work through the following steps:
State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis. Null hypothesis: P1 = P2 Alternative hypothesis: P1 ≠ P2 Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the proportion of population 1 is too large or too small.
Formulate an analysis plan. For this analysis, the significance level is 0.05. The test method is a two-sided z-test.
Analyze the sample data. Using the sample data, we calculated the proportion of the pooled sample (p) and the standard error (SE). Using these measures, we compute the z-score (z) test statistic. The analysis described above is a two-proportion z-test.
Interpretation of results If the sample results are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P value with the significance level and rejecting the null hypothesis when the P value is less than the significance level. Hypothesis test: difference between proportions This lesson explains how to perform a hypothesis test to determine if the difference between two proportions is significant. The test procedure, called the two-sided z-test, is appropriate when the following conditions are met:
The sampling method for each population is a simple random sampling.
The samples are independent.
Each champion includes at least 10 successes and 10 failures.
Each population is at least 20 times larger than its sample.
This approach involves four phases: (1) declaring the hypotheses, (2) formulating an analysis plan, (3) analyzing the sample data, and (4) interpreting the results. State hypotheses Each hypothesis test requires the analyst to declare a null hypothesis and an alternative hypothesis. The following table shows three sets of hypotheses. Each makes a statement about the difference d between two proportions of the population, P1 and P2. (In the table, the symbol ≠ means "not equal to").
Set | Null hypothesis | Alternative hypothesis | Number of tails |
1 | P1 - P2 = 0 | P1 - P2 ≠ 0 | 2 |
2 | P1 - P2 > 0 | P1 - P2 < 0 | 1 |
3 | P1 - P2 < 0 | P1 - P2 > 0 | 1 |
- The first set of hypotheses (Set 1) is an example of a two-tailed test, since an extreme value on both sides of the sampling distribution would induce an investigator to reject the null hypothesis. The other two sets of hypotheses (sets 2 and 3) are one-tailed tests, since an extreme value on one side of the sampling distribution would induce an investigator to reject the null hypothesis.
- When the null hypothesis states that there is no difference between the two proportions of the population (i.e., d = P1 - P2 = 0), the null and alternative hypothesis for a two-tailed test is often stated as follows.
- I have: P1 = P2
- Has: P1 ≠ P2
- Formulate an analysis plan.
- The analysis plan describes how to use the sample data to accept or reject the null hypothesis. You must specify the following elements.
- Level of significance. Researchers often choose significance levels of 0.01, 0.05, or 0.10; but you can use any value between 0 and 1.
- Test method. Use the two aspect ratio z test (described in the next section) to determine if the assumed difference between population proportions differs significantly from the observed difference in the sample.
- Analyze the sample data.
- Using the sample data, complete the following calculations to find the test statistic and associated P-value.
- Proportion of the aggregate sample. Since the null hypothesis states that P1 = P2, we use an aggregate sample proportion (p) to calculate the standard error of the sampling distribution.
- p = (p1 * n1 + p2 * n2) / (n1 + n2)
- Where p1 is the proportion of the sample from population 1, p2 is the proportion of the sample from population 2, n1 is the size of sample 1 and n2 is the size of sample 2.
- Standard error. Calculate the standard error (SE) of the sampling distribution difference between two proportions.
- SE = sqrt {p * (1 - p) * [(1 / n1) + (1 / n2)]}
- Where p is the proportion of the pooled sample, n1 is the size of sample 1 and n2 is the size of sample 2.
- Statistical test. The test statistic is a z (z) score defined by the following equation.
- z = (p1 - p2) / SE
- Where p1 is the proportion of sample 1, p2 is the proportion of sample 2 and SE is the standard error of the sampling distribution.
- p-value The P value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a z-score, use the normal distribution calculator to assess the probability associated with the z-score. (See the example problems at the end of this lesson for examples of how this is done.)
- The analysis described above is a two-way z-test.
- Interpretation of results
- If the sample results are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P value with the significance level and rejecting the null hypothesis when the P value is less than the significance level.
- Test your understanding
- In this section, two sample problems illustrate how to perform a hypothesis test for the difference between two proportions. The first problem involves a two-tailed test; The second problem, a tail test.
- Problem 1: two-tailed test
- Suppose Acme Drug Company develops a new drug, designed to prevent colds. The company claims that the drug is equally effective for men and women. To test this claim, they chose a simple random sample of 100 women and 200 men from a population of 100,000 volunteers.
- At the end of the study, 38% of the women had a cold; and 51% of men caught a cold. Based on these results, can we rule out the company's claim that the drug is equally effective for men and women? Use a significance level of 0.05.
- Solution: The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results. We work through the following steps:
- State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis.
- Null hypothesis: P1 = P2
- Alternative hypothesis: P1 ≠ P2
- Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the proportion of population 1 is too large or too small.
- Formulate an analysis plan. For this analysis, the significance level is 0.05. The test method is a two-sided z-test.
- Analyze the sample data. Using the sample data, we calculated the proportion of the pooled sample (p) and the standard error (SE). Using these measures, we compute the z-score (z) test statistic.
- p = (p1 * n1 + p2 * n2) / (n1 + n2)
- p = [(0.38 * 100) + (0.51 * 200)] / (100 + 200)
- p = 140/300 = 0.467
- SE = sqrt {p * (1 - p) * [(1 / n1) + (1 / n2)]}
- SE = sqrt [0.467 * 0.533 * (1/100 + 1/200)]
- SE = sqrt [0.003733] = 0.061
- z = (p1 - p2) / SE = (0.38 - 0.51) /0.061 = -2.13
- Where p1 is the proportion of the sample in sample 1, where p2 is the proportion of the sample in sample 2, n1 is the size of sample 1 and n2 is the size of sample 2.
- Since we have a two-tailed test, the P value is the probability that the z-score is less than -2.13 or greater than 2.13.
- We use the normal distribution calculator to find P (z <-2.13) = 0.017 and P (z> 2.13) = 0.017. Therefore, the value P = 0.017 + 0.017 = 0.034.
- Interpret the results. Since the P value (0.034) is lower than the significance level (0.05), we cannot accept the null hypothesis.
- Note: If you use this approach during an exam, you can also mention why this approach is appropriate. In particular, the approach is appropriate because the sampling method was simple random sampling, the samples were independent, each population was at least 10 times larger than its sample, and each sample included at least 10 successes and 10 failures.
- Problem 2: testing a queue
- Suppose the previous example is declared slightly differently. Suppose Acme Drug Company develops a new drug, designed to prevent colds. The company claims that the drug is more effective for women than for men. To test this claim, they chose a simple random sample of 100 women and 200 men from a population of 100,000 volunteers.
- At the end of the study, 38% of the women had a cold; and 51% of men caught a cold. Based on these results, can we conclude that the medication is more effective for women than for men? Use a significance level of 0.01.
- Solution: The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results. We work through the following steps:
- State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis.
- Null hypothesis: P1> = P2
- Alternative hypothesis: P1 <P2
- Note that these hypotheses constitute a one-tailed test. The null hypothesis will be rejected if the percentage of women who have a cold (p1) is sufficiently lower than the proportion of men who have a cold (p2).
- Formulate an analysis plan. For this analysis, the significance level is 0.01. The test method is a two-sided z-test.
- Analyze the sample data. Using the sample data, we calculated the proportion of the pooled sample (p) and the standard error (SE). Using these measures, we compute the z-score (z) test statistic.
p = (p1 * n1 + p2 * n2) / (n1 + n2)
p = [(0.38 * 100) + (0.51 * 200)] / (100 + 200)
p = 140/300 = 0.467
SE = sqrt{ p * ( 1 - p ) * [ (1/n1) + (1/n2) ] }
SE = sqrt[ 0.467 * 0.533 * ( 1/100 + 1/200 ) ]
SE = sqrt [0.003733] = 0.061
z = (p1 - p2) / SE = (0.38 - 0.51)/0.061 = -2.13
Where p1 is the proportion of the sample in sample 1, where p2 is the proportion of the sample in sample 2, n1 is the size of sample 1 and n2 is the size of sample 2.
Subsequently we have a one-tailed test, the P significance is the probability that the z-score is less than -2.13. We practice the normal distribution calculator to discover P (z <-2.13) = 0.017. Therefore, the P value = 0.017.
Interpret the results. Since the P value (0.017) is greater than the significance level (0.01), we cannot reject the null hypothesis
5.2. Difference of proportions
To estimate the difference between two population proportions with a confidence interval, you can use the Central Limit Theorem when the sample sizes are large enough (typically, each at least 30). When a statistical characteristic, such as opinion on an issue (support/don’t support), of the two groups being compared is categorical, people want to report on the differences between the two population proportions — for example, the difference between the proportion of women and men who support a four-day work week. How do you do this?
You estimate the difference between two population proportions, p1 – p2, by taking a sample from each population and using the difference of the two sample proportions,
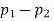
Plus or minus a margin of error. The result is called a confidence interval for the difference of two population proportions, p1 – p2.
The formula for a confidence interval (CI) for the difference between two population proportions is
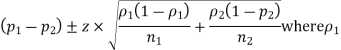
And n1 are the sample proportion and sample size of the first sample, and 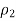

And n2 are the sample proportion and sample size of the second sample. The value z* is the appropriate value from the standard normal distribution for your desired confidence level. (Refer to the following table for z*-values.)
z*–values for Various Confidence Levels
Confidence Level | z*-value |
80% | 1.28 |
90% | 1.645 (by convention) |
95% | 1.96 |
98% | 2.33 |
99% | 2.58 |
To calculate a CI for the difference between two population proportions, do the following:
- Determine the confidence level and find the appropriate z*-value.
Refer to the above table.
2. Find the sample proportion
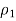
For the first sample by taking the total number from the first sample that are in the category of interest and dividing by the sample size, n1. Similarly, find 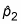 for the second sample.
for the second sample.
3. Take the difference between the sample proportions,
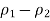
4. Find
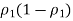
And divide that by n1. Find
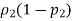
And divide that by n2. Add these two results together and take the square root.
5. Multiply z* times the result from Step 4.
This step gives you the margin of error.
6. Take
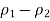
Plus or minus the margin of error from Step 5 to obtain the CI.
The lower end of the CI is
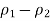
Minus the margin of error, and the upper end of the CI is
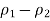
Plus the margin of error.
The formula shown here for a CI for p1 – p2 is used under the condition that both of the sample sizes are large enough for the Central Limit Theorem to be applied and allow you to use a z*-value; this is true when you are estimating proportions using large scale surveys, for example. For small sample sizes, confidence intervals are beyond the scope of an intro statistics course.
Suppose you work for the Las Vegas Chamber of Commerce, and you want to estimate with 95% confidence the difference between the percentage of all females who have ever gone to see an Elvis impersonator and the percentage of all males who have ever gone to see an Elvis impersonator, in order to help determine how you should market your entertainment offerings.
- Because you want a 95% confidence interval, your z*-value is 1.96.
- Suppose your random sample of 100 females includes 53 females who have seen an Elvis impersonator, so
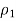
Is 53 divided by 100 = 0.53. Suppose also that your random sample of 110 males includes 37 males who have ever seen an Elvis impersonator, so
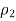
Is 37 divided by 110 = 0.34.
3. The difference between these sample proportions (females – males) is 0.53 – 0.34 = 0.19.
4. Take 0.53 ∗ (1 – 0.53) to obtain 0.2941. Then divide that by 100 to get 0.0025. Then take 0.34 ∗ (1 – 0.34) to obtain 0.2244. Then divide that by 110 to get 0.0020. Add these two results to get 0.0025 + 0.0020 = 0.0045. Then find the square root of 0.0045 which is 0.0671.
5. 1.96 ∗ 0.0671 gives you 0.13, or 13%, which is the margin of error.
6. Your 95% confidence interval for the difference between the percentage of females who have seen an Elvis impersonator and the percentage of males who have seen an Elvis impersonator is 0.19 or 19% (which you got in Step 3), plus or minus 13%. The lower end of the interval is 0.19 – 0.13 = 0.06 or 6%; the upper end is 0.19 + 0.13 = 0.32 or 32%.
To interpret these results within the context of the problem, you can say with 95% confidence that a higher percentage of females than males have seen an Elvis impersonator, and the difference in these percentages is somewhere between 6% and 32%, based on your sample.
The temptation is to say, “Well, I knew a greater proportion of women has seen an Elvis impersonator because that sample proportion was 0.53 and for men it was only 0.34. Why do I even need a confidence interval?” All those two numbers tell you is something about those 210 people sampled. You also need to factor in variation using the margin of error to be able to say something about the entire populations of men and women.
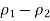
For example, if you had switched the males and females, you would have gotten –0.19 for this difference. That’s okay, but you can avoid negative differences in the sample proportions by having the group with the larger sample proportion serve as the first group (here, females).
However, even if the group with the larger sample proportion serves as the first group, sometimes you will still get negative values in the confidence interval. Suppose in the above example that only 0.43 of women had seen an Elvis impersonator. Thus, the difference in proportions is 0.09, and the upper end of the confidence interval is 0.09 + 0.13 = 0.22 while the lower end is 0.09 – 0.13 = –0.04. This means that the true difference is reasonably anywhere from 22% more women to 4% more men. It’s too close to tell for sure.
5.3. Single mean, Difference of means and difference of standard deviations
The single mean (or one-sample) t-test is used to compare the mean of a variable in a sample of data to a (hypothesized) mean in the population from which our sample data are drawn. This is important because we seldom have access to data for an entire population. The hypothesized value in the population is specified in the Comparison value box.
We can perform either a one-sided test (i.e., less than or greater than) or a two-sided test (see the Alternative hypothesis dropdown). We use one-sided tests to evaluate if the available data provide evidence that the sample mean is larger (or smaller) than the comparison value (i.e., the population value in the null-hypothesis)
Example :
We have access to data from a random sample of grocery stores in the UK. Management will consider entering this market if consumer demand for the product category exceeds 100M units, or, approximately, 1750 units per store. The average demand per store in the sample is equal to 1953. While this number is larger than 1750 we need to determine if the difference could be attributed to sampling error.
You can find the information on unit sales in each of the sample stores in the demand_uk.rda data set. The data set contains two variables, store_id and demand_uk. Our null-hypothesis is that the average store demand in the UK is equal to 1750 unit so we enter that number into the Comparison value box. We choose the Greater than option from the Alternative hypothesis drop-down because we want to determine if the available data provides sufficient evidence to reject the null-hypothesis favor of the alternative that average store demand in the UK is larger than 1750.
The first two blocks of output show basic information about the test (e.g.,. The null and alternative hypothesis) and summary statistics (e.g., mean, standard deviation, standard error, margin or error, etc.). The final row of output shows the following:
- Diff is the difference between the sample mean (1953.393) and the comparison value (1750)
- Se is the standard error (i.e., the standard deviation of the sampling distribution of diff)
- t.value is the t statistic associated with diff that we can compare to a t-distribution (i.e., diff / se)
- p.value is the probability of finding a value as extreme or more extreme than diff if the null hypothesis is true
- Df is the degrees of freedom associated with the statistical test (i.e., n - 1)
- 5% 100% show the 95% confidence interval around the sample mean (1897 to Inf.). These numbers provide a range within which the true population mean is likely to fall
Significance test of difference between sample means
Given two independent examples 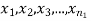 and
and 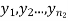 with means
with means 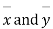 standard derivations
standard derivations 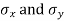 from a normal population with the same variance, we have to test the hypothesis that the population means
from a normal population with the same variance, we have to test the hypothesis that the population means 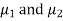 are same For this, we calculate
are same For this, we calculate
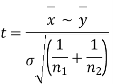
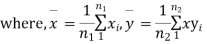
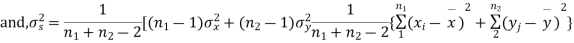
It can be shown that the variate t defined by (1) follows the t distribution with 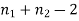 degrees of freedom.
degrees of freedom.
If the calculated value 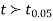 the difference between the sample means is said to be significant at 5% level of significance.
the difference between the sample means is said to be significant at 5% level of significance.
If 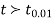 , the difference is said to be significant at 1% level of significance.
, the difference is said to be significant at 1% level of significance.
If 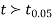 the data is said to be consistent with the hypothesis that
the data is said to be consistent with the hypothesis that 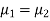 .
.
Cor. If the two samples are of same size and the data are paired, then t is defined by
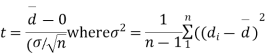
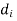 =difference of the ith member of the sample
=difference of the ith member of the sample
d=mean of the differences =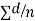 and the member of d.f.=n-1.
and the member of d.f.=n-1.
Example Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
Sol. We compute the mean and the S.D. Of the difference between the marks of the two tests as under:
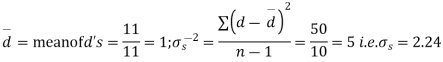
Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.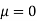
Then, 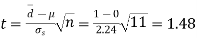 nearly and df v=11-1=10
nearly and df v=11-1=10
Students | 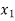 | 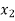 | 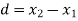 | 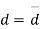 | 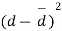 |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
| 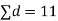 |
| 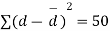 |
- From table IV, we find that
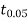 (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of 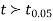 , the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
Example:
- From a random sample of 10 pigs fed on diet A, the increase in weight in certain period were 10,6,16,17,13,12,8,14,15,9 lbs. For another random sample of 12 pigs fed on diet B, the increase in the same period were 7,13,22,15,12,14,18,8,21,23,10,17 lbs. Test whether diets A and B differ significantly as regards their effect on increases in weight ?
- Sol. We calculate the means and standard derivations of the samples as follows
| Diet A |
|
| Diet B |
|
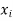 | 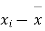 | 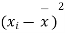 | 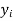 | 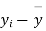 | 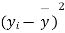 |
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 13 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 17 | 2 | 4 |
|
|
|
|
|
|
120 |
|
| 180 | 0 | 314 |
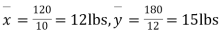
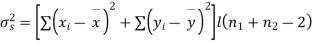
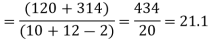
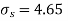
Assuming that the samples do not differ in weight so far as the two diets are concerned i.e. 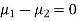
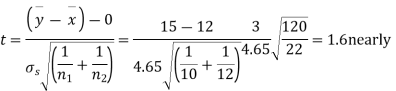
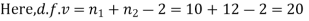
For v=20, we find 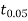 =2.09
=2.09
The calculated value of 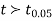
Hence the difference between the samples means is not significant i.e. thew two diets do not differ significantly as regards their effects on increase in weight.
Module-6
Small samples
6.1. Test for single mean
When you test a single mean, you’re comparing the mean value to some other hypothesized value. Which test you run depends on if you know the population standard deviation (σ) or not.
Known population standard deviation
If you know the value for σ, then the population mean has a normal distribution: use a one sample z-test. The z-test uses a formula to find a z-score, which you compare against a critical value found in a z-table. The formula is:
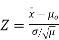
A one sample test of means compares the mean of a sample to a pre-specified value and tests for a deviation from that value. For example we might know that the average birth weight for white babies in the US is 3,410 grams and wish to compare the average birth weight of a sample of black babies to this value.
Assumptions
- Independent observations.
- The population from which the data is sampled is normally distributed.
Hypothesis:
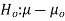
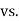
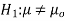
Where μ0 is a pre-specified value (in our case this would be 3,410 grams).
Test Statistic
- First calculate
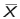 , the sample mean.
, the sample mean. - We choose an α = 0.05 significance level
- If the standard deviation is known:
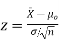
Using the significance level of 0.05, we reject the null hypothesis if z is greater than 1.96 or less than -1.96.
- If the standard deviation is unknown:
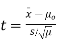
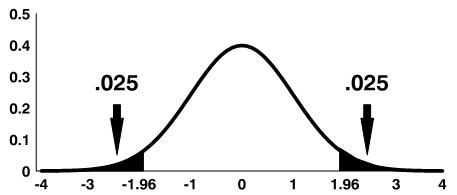
Using the significance level of 0.05, we reject the null hypothesis if |t| is greater than the critical value from a t-distribution with df = n-1.
Note: The shaded area is referred to as the critical region or rejection region.
We can also calculate a 95% confidence interval around the mean. The general form for a confidence interval around the mean, if σ is unknown, is
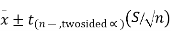
For a two-sided 95% confidence interval, use the table of the t-distribution (found at the end of the section) to select the appropriate critical value of t for the two-sided α=0.05.
Example: one sample t-test
Recall the data used in module 3 in the data file "dixonmassey."
Data dixonmassey;
Input Obs chol52 chol62 age cor dchol agelt50 $;
Datalines;
1 | 240 | 209 | 35 | 0 | -31 | y |
2 | 243 | 209 | 64 | 1 | -34 | n |
3 | 250 | 173 | 61 | 0 | -77 | n |
4 | 254 | 165 | 44 | 0 | -89 | y |
5 | 264 | 239 | 30 | 0 | -25 | y |
6 | 279 | 270 | 41 | 0 | -9 | y |
7 | 284 | 274 | 31 | 0 | -10 | y |
8 | 285 | 254 | 48 | 1 | -31 | y |
9 | 290 | 223 | 35 | 0 | -67 | y |
10 | 298 | 209 | 44 | 0 | -89 | y |
11 | 302 | 219 | 51 | 1 | -83 | n |
12 | 310 | 281 | 52 | 0 | -29 | n |
13 | 312 | 251 | 37 | 1 | -61 | y |
14 | 315 | 208 | 61 | 1 | -107 | n |
15 | 322 | 227 | 44 | 1 | -95 | y |
16 | 337 | 269 | 52 | 0 | -68 | n |
17 | 348 | 299 | 31 | 0 | -49 | y |
18 | 384 | 238 | 58 | 0 | =146 | n |
19 | 386 | 285 | 33 | 0 | -101 | y |
20 | 520 | 325 | 40 | 1 | -195 | y |
;
Many doctors recommend having a total cholesterol level below 200 mg/dl. We will test to see if the 1952 population from which the Dixon and Massey sample was gathered is statistically different, on average, from this recommended level.
- H0: μ = 200 vs. H1: μ ≠ 200
- α=0.05
- Our sample of n=20 has
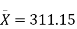 = 311.15 and s = 64.3929.
= 311.15 and s = 64.3929. - Df = 19, so reject H0 if |t| > 2.093
Calculate:
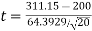
|t| > 2.093 so we reject H0
The 95% confidence limits around the mean are
311.15 ± (2.093)(64.3929/√20)
311.15 ± 30.14
(281.01, 341.29)
One Sample t-test Using SAS:
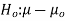
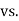
Proc ttest data=name h0=μ0 alpha=α;
Var var;
Run;
SAS uses the stated α for the level of confidence (for example, α=0.05 will result in 95% confidence limits). For the hypothesis test, however, it does not compute critical values associated with the given α, and compare the t-statistic to the critical value. Rather, SAS will provide the p-value, the probability that T is more extreme than observed t. The decision rule, "reject if |t| > critical value associated with α" is equivalent to "reject if p < α."
SAS will provide the p value, the probability that T is more extreme than observed t. The decision rule, “reject if |t|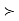 critical value associated with
critical value associated with 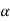 ” is equivalent to “reject if p
” is equivalent to “reject if p 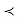 a.”
a.”
Example:
Proc ttest data=dixonmassey h0=200 alpha=0.05;
Var chol52;
Title 'One Sample t-test with proc ttest';
Title2 'Testing if the sample of cholesterol levels in 1952 is statistically different from 200' ;
Run;
One sample t-test with proc ttest
‘Testing if the sample of cholesterol level in 1952 is statistically different from
The T TEST Procedure
Variable : chol52
N | Mean | Std Dev | Std Err | Minimum | Maximum |
20 | 311.2 | 64.3929 | 14.3987 | 240.0 | 520.0 |
Mean | 95% CL Mean | Std Dev | 95% CL | Std Dev |
311.2 | 281.0 | 64.3929 | 48.9702 | 94.0505 |
DF | T Value | Pr> |t| |
19 | 7.72 | <.0001 |
As in our hand calculations, t = 7.72, and we reject H0 (because p<0.0001 which is < 0.05, our selected α level).
The mean cholesterol in 1952 was 311.2, with 95% confidence limits (281.0, 341.3).
6.2. Difference for means and correlations coefficients
Testing the meaning of the correlation coefficient.
The relationship coefficient, r, tells us about the strength and direction of the linear relationship between X1 and X2.
Sample data is used to calculate r, the correlation coefficient for the sample. If we had data for the entire population, we could find the correlation coefficient for the population.
But since we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r, is our estimate of the correlation coefficient for the unknown population.
• ρ = population correlation coefficient (unknown)
• r = sample relationship coefficient (known; calculated from sample data)
The hypothesis test allows us to decide if the value of the population correlation coefficient ρ is "close to zero" or "significantly different from zero". We decide on the basis of the correlation coefficient of sample r and the size of sample n.
If the test arranges that the relationship coefficient is meaningfully different from zero, we say that the relationship coefficient is "significant".
• Conclusion: there is sufficient evidence to conclude that there is a significant linear relationship between X1 and X2 because the correlation coefficient is significantly different from zero.
• Meaning of the conclusion: there is a significant linear relationship X1 and X2. If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that the correlation coefficient is not "significant".
Take the hypothesis test
• Null hypothesis: H0: ρ = 0
• Alternative hypothesis: Ha: ρ≠ 0
What do hypotheses mean in words?
• Hypothesis H0: the population correlation coefficient is NOT meaningfully dissimilar from zero. There is NO significant linear relationship (correlation) between X1 and X2 in the population.
• Alternative hypothesis Ha: the population correlation coefficient is significantly different from zero. Here is a significant linear relationship (correlation) amid X1 and X2 in the population.
Drawing a conclusion There are two methods of making a hypothetical decision. The test statistic to test this hypothesis is:
When the second formula is an equivalent form of the test statistic, n is the sample size and the degrees of freedom are n-2. This is a t-statistic and works in the same way as other t-tests.
Calculate the value t and compare it to the critical value in table t at the appropriate degrees of freedom and the level of confidence you want to maintain. If the calculated value is in the queue, then you cannot accept the null hypothesis that there is no linear relationship between these two independent random variables.
If the calculated t value is NOT in the queue, it is not possible to reject the null hypothesis that there is no linear relationship between the two variables.
A quick way to test correlations is the relationship between sample size and correlation. Me:
Then this implies that the correlation between the two variables demonstrates the existence of a linear relationship and is statistically significant at approximately the significance level of 0.05.
As the formula indicates, there is an inverse relationship between the sample size and the required correlation for the meaning of a linear relationship.
With only 10 observations, the required correlation for significance is 0.6325, for 30 observations the required correlation for significance drops to 0.3651 and for 100 observations the required level is only 0.2000.
Correlations can be useful for visualizing data, but are not used appropriately to "explain" a relationship between two variables. Perhaps a single statistic is not used more inadequately than the correlation coefficient.
Quoting correlations between health conditions and anything from place of residence to eye color has the effect of implying a cause and effect relationship. This simply cannot be accomplished with a correlation coefficient.
The correlation coefficient is obviously innocent of this misinterpretation. The analyst has a duty to use a statistic designed to test cause and effect relationships and report those results only if he intends to submit such a request.
The problem is that passing this stricter test is difficult, so lazy and / or unscrupulous "investigators" turn to correlations when they cannot legitimately support their case.
Define a t-test of a regression coefficient and provide a unique example of its use. Definition: A t-test is obtained by dividing a regression coefficient by its standard error and then comparing the result with critical values for students with df error.
Provides a test for the claim that when all other variables were included in the relevant regression model. Example: Suppose that 4 variables are suspected to influence some response. Suppose the assembly results include:
Variable | Regression coefficient | Standard error of regular coefficient |
.5 | 1 | -3 |
.4 | 2 | +2 |
.02 | 3 | +1 |
.6 | 4 | -.5 |
- t calculated for variables 1, 2 and 3 would be 5 or greater in absolute value while for variable 4 it would be less than 1. For most levels of significance, the hypothesis would be rejected. However, note that this is the case where, and have been included in the regression. For most levels of significance, the hypothesis would have continued (held) for the case where, and are in regression. Often this pattern of results will involve calculating another regression involving only and examining the proportions produced for that case.
- The correlation between the scores on a neuroticism test and the scores on an anxiety test is high and positive; Thus
- To. Anxiety causes neuroticism
- Yes. Those who score low on one test tend to score high on the other.
- C. Those who score small on one test tend to score low on the other.
- Re. You cannot make a meaningful prediction from one test to another.
- C. Those who score small on one test tend to score low on the additional.
- Testing the meaning of the correlation coefficient.
- LEARNING OUTCOMES
- • Calculate and interpret the correlation coefficient.
- The correlation coefficient, r, says us about the asset and direction of the linear relationship amid x and y. However, the reliability of the linear model also depends on the number of data points observed in the sample. We have to examine together the value of the correlation coefficient r and the sample size n.
- We done a hypothesis test on the "significance of the correlation coefficient" to choose whether the linear relationship in the sample data is strong sufficient to be used to model the connection in the population.
- Sample data is used to calculate r, the correlation coefficient for the sample. If we had data for the entire population, we could find the correlation coefficient for the population. But since we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r, is our estimate of the correlation coefficient for the unknown population.
- • The representation for the population correlation coefficient is ρ, the Greek letter "rho".
- ρ = population correlation coefficient (unknown)
- r = sample correlation coefficient (known; calculated from sample data)
- The hypothesis test allows us to decide if the value of the population correlation coefficient
- ρ is "near to zero" or "significantly dissimilar from zero". We decide on the basis of the correlation coefficient of sample r and the size of sample n.
- If the test determines that the correlation coefficient is meaningfully dissimilar from zero, we say that the association coefficient is "significant".
- Assumption: there is sufficient indication to accomplish that there is a important linear relationship between x and y, since the association coefficient is significantly dissimilar from zero. What does the conclusion mean: There is a significant linear relationship between x and y. We can practice the reversion line to model the linear relationship amid x and y in the population.
- If the test achieves that the correlation coefficient is not meaningfully diverse from zero (it is close to zero), we say that the correlation coefficient is not "significant".
- Assumption: “There is insufficient indication to accomplish that there is a significant linear relationship amid
- x and y because the correlation coefficient is not meaningfully dissimilar from zero. "What the conclusion means: There is no important linear association between x and y. So, we CANNOT use the reversion line to model a linear relationship amid x and y in the population.
- Note
- • If r is significant and the scatter diagram shows a linear trend, the line can be used to predict the value of y for the values of x that fall within the domain of the observed values of x.
- • If r is not significant OR if the scatter diagram does not show a linear trend, the line should not be used for forecasting.
- • If r is significant and if the scatter diagram shows a linear trend, the line may NOT be appropriate or reliable to predict OUT of the domain of the x values observed in the data.
- Take the hypothesis test
- Null hypothesis: H0: ρ = 0
- Alternative hypothesis: Ha: ρ≠ 0
- What do hypotheses mean in words?
- Hypothesis H0: the population relationship coefficient is NOT meaningfully dissimilar from zero. There is NO significant linear relationship (correlation) between x and y in the population.
- Alternative hypothesis Ha: the population correlation coefficient is significantly different from zero. There is a important linear relationship (correlation) between x and y in the population.
- Get a conclusion
- There are two methods of making the decision. The two methods are equivalent and give the same result.
- Method 1: using the p value
- Method 2: use of a table of critical values.
- In this chapter of this textbook, we will continuously use a significance level of 5%, α = 0.05
Note
- Using the p-value method, you can choose any appropriate level of significance desired; It is not limited to the use of α = 0.05. But the critical value table provided in this textbook assumes that we are using a significance level of 5%, α = 0.05. (If we wanted to use a significance level other than 5% with the critical value method, we would need several tables of critical values that are not provided in this manual).
- Method 1: use a p-value to make a decision
- To calculate the p-value using LinRegTTEST:
- • On the LinRegTTEST input screen, at the line prompt for β or ρ, highlight "≠ 0"
- The output screen shows the p value on the line that says "p =".
- (Most statistical software can calculate the p-value).
- If the p value is fewer than the meaning level (α = 0.05)
- Decision: reject the null hypothesis.
- Assumption: "There is sufficient indication to accomplish that there is aimportant linear relationship amid x and y since the correlation coefficient is meaningfullydissimilar from zero."
- If the p value is NOT less than the meaning level (α = 0.05)
- Decision: DO NOT reject the null hypothesis.
- Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is NOT significantly different from zero."
- Calculation Notes:
- Use technology to calculate the p-value. The calculations for calculating test statistics and p-value are described below:
- The p-value is considered using a t-distribution with n - 2 degrees of freedom.
- The formula for the test statistic is t = r√n - 2√1 - r2t = rn - 21 - r2. The test statistic value, t, is displayed on the computer or calculator output along with the p-value. The t-test statistic has the same sign as the correlation coefficient r.
- The p-value is the combined area in both tails.
6.3. Test for ratio of variances: Chi-square test for goodness of fit and independent of attributes.
Chi-square test for independence
This lesson explains how to take a chi-square test for independence. The test is useful when you have two definite variables from a single population.
It is used to determine if there is a significant association between the two variables.
For example, in an electoral poll, voters could be classified by gender (male or female) and voting preference (democratic, republican, or independent).
We could use a chi-square test for independence to determine if gender is linked to voting preference. The example problem at the end of the lesson considers this example.
When to use the Chi-square test for independence
The testing procedure described in this lesson is appropriate when the following conditions are true:
The sample method is a simple random sampling.
The variables under consideration are categorical.
If the sample data is showed in a likelihood table, the predictable frequency total for each cell in the table is at least 5.
This approach involves four phases: (1) declaring the hypotheses, (2) formulating an analysis plan, (3) analyzing the sample data, and (4) interpreting the results.
State hypotheses
Suppose that variable A has levels r and that variable B has levels c. The null hypothesis establishes that knowing the level of variable A does not help to predict the level of variable B.
That is, the variables are independent.
Ho: variable A and variable B are independent.
Ha: variables A and B are not independent.
The another hypothesis is that meaningful the level of flexible A can help you expect the level of variable B.
Note: support for the another hypothesis proposes that the variables are connected; but the connection is not essentially connecting, in the sense that one variable "causes" the other.
Formulate an analysis plan.
The analysis plan describes how to use the sample data to accept or reject the null hypothesis. The plan must specify the following elements.
Level of significance. Researchers often choose significance levels of 0.01, 0.05, or 0.10; but you can use any value between 0 and 1.
Test method. Use the chi-square test to determine independence to determine if there is a significant relationship between two categorical variables.
Analyze the sample data.
Using the sample data, find the degrees of freedom, the predictable frequencies, the test statistic, and the P value associated with the test statistic. The method defined in this unit is showed in the sample problematic at the end of this lesson.
Degrees of freedom. The degrees of freedom (DF) are equal to:
DF = (r - 1) * (c - 1)
Where r is the number of levels for one catabolic variable and c is the number of levels for the other categorical variable.
You predictable frequencies. The predictable frequency counts are considered distinctly for each level of one definite variable at each level of the other categorical variable.
Calculate the predictable frequencies r * c, according to the following formula.
Er, c = (nr * nc) / n
Where Er, c is the predictable frequency count for level r of variable A and level c of variable B, nr is the total number of sample explanations at level r of variable A, nc is the total number of sample explanations at level c of variable B, en is the total sample size.
Statistical test. The test statistic is a chi-square (Χ2) random variable defined by the following equation.
Χ2 = Σ[ (Or,c - Er,c)2 / Er,c ]
Where O, c is the observed frequency count at level r of variable A and level c of variable B, and Er, c is the predicted frequency count at level r of adjustable A and level c of adjustable B.
p-value The P value is the probability of detecting a sample figure as exciting as the test statistic.
Meanwhile the test measurement is a chi-square, use the Chi-square supply calculator to measure the probability related with the test statistic. Use the degrees of freedom considered above.
Interpretation of results
If the sample results are unlikely, given the null hypothesis, the researcher rejects the null hypothesis.
Typically, this involves comparing the P value with the significance level and rejecting the null hypothesis when the P value is less than the significance level.
Test your understanding:
A public opinion poll analyzed a simple random sample of 1,000 voters. Respondents were classified by gender (male or female) and by voting preference (Republican, Democratic, or Independent).
The effects are shown in the possibility table below.
| Voting Preferences | Row total | ||
Rep | Dem | Ind | ||
Male | 200 | 150 | 50 | 400 |
Female | 250 | 300 | 50 | 600 |
Column total | 450 | 450 | 100 | 1000 |
- Is there a gender gap? Do men's voting preferences differ significantly from women's preferences? Use a significance level of 0.05. Solution The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results.
- We work through the following steps:
State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis. Ho: Gender and voting preferences are independent. Ha: Gender and voting preferences are not independent.
Formulate an analysis plan. For this analysis, the significance level is 0.05. Using sample data, we will perform a chi-square test for independence.
Analyze the sample data. By applying the chi-square test for independence to the sampling data, we calculated degrees of freedom, predictable frequency counts, and chi-square test statistics.
Based on the chi-square statistic and the degrees of freedom, we determine the value P..
DF = (r - 1) * (c - 1) = (2 - 1) * (3 - 1) = 2
Er,c = (nr * nc) / n
E1,1 = (400 * 450) / 1000 = 180000/1000 = 180
E1,2 = (400 * 450) / 1000 = 180000/1000 = 180
E1,3 = (400 * 100) / 1000 = 40000/1000 = 40
E2,1 = (600 * 450) / 1000 = 270000/1000 = 270
E2,2 = (600 * 450) / 1000 = 270000/1000 = 270
E2,3 = (600 * 100) / 1000 = 60000/1000 = 60
Χ2 = Σ [ (Or,c - Er,c)2 / Er,c ]
Χ2 = (200 - 180)2/180 + (150 - 180)2/180 + (50 - 40)2/40
+ (250 - 270)2/270 + (300 - 270)2/270 + (50 - 60)2/60
Χ2 = 400/180 + 900/180 + 100/40 + 400/270 + 900/270 + 100/60
Χ2 = 2.22 + 5.00 + 2.50 + 1.48 + 3.33 + 1.67 = 16.2
Where DF is the degree of freedom, r is the number of levels of gender, c is the number of levels of the voting preference, nr is the number of observations of level r of gender, nc is the number of observations of level c of voting preference, n is the number of observations in the sample, Er, c is the predicted frequency count when gender is level r and voting preference is level c, and O, c is the observed frequency count when gender is level r, voting preference is level c.
The P value is the probability that a chi-square statistic with 2 degrees of freedom is more extreme than 16.2.
We use the Chi-Square distribution calculator to find P (Χ2> 16.2) = 0.0003.
Interpret the results. Since the P value (0.0003) is lower than the significance level (0.05), we cannot accept the null hypothesis.
Therefore, we conclude that there is a relationship between gender and voting preference.
UNIT-4
Applied statistics (Module-5 contd.)-
Module-6
Small sample
5.1. Test of significance: Large sample test for single proportion
Large Sample Test for a Proportion
- The sampling distribution of
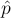 is approximately normal.
is approximately normal. - Use the value of p in the null hypothesis when computing the standard deviation of
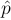 .
. - The test statistic is
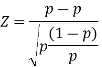
Hypothesis Test: Difference Between Proportions
This lesson describes how to conduct a hypothesis test to define whether the difference between two proportions is significant.
The test procedure, called the two-proportion z-test, is suitable when the following conditions are met:
- The sampling method for each population is simple random sample.
- The examples are independent.
- Each example comprises at least 10 attainments and 10 failures.
- Each population is at least 20 times as big as its example.
This approach contains of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.
Test Your Considerate
In this section, two sample difficulties illustrate how to conduct a hypothesis test for the difference between two sizes. The first problem includes two-tailed test; the second problem, a one-tailed test.
Problem 1: Two-Tailed Test
Suppose Acme Drug Company is making a new medicine designed to prevent colds. The company claims that the drug is equally effective for men and women. To test this claim, they chose a simple random sample of 100 women and 200 men from a population of 100,000 volunteers.
At the end of the study, 38% of the women had a cold; and 51% of men caught a cold. Based on these results, can we rule out the company's claim that the drug is equally effective for men and women? Use a significance level of 0.05.
Solution: The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results. We work through the following steps:
State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis.
Null hypothesis: P1 = P2
Alternative hypothesis: P1 ≠ P2
Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the proportion of population 1 is too large or too small.
Formulate an analysis plan. For this analysis, the significance level is 0.05. The test method is a two-sided z-test.
Analyze the sample data. Using the sample data, we calculated the proportion of the pooled sample (p) and the standard error (SE). Using these measures, we compute the z-score (z) test statistic.
p = (p1 * n1 + p2 * n2) / (n1 + n2)
p = [(0.38 * 100) + (0.51 * 200)] / (100 + 200)
p = 140/300 = 0.467
SE = sqrt{ p * ( 1 - p ) * [ (1/n1) + (1/n2) ] }
SE = sqrt[ 0.467 * 0.533 * ( 1/100 + 1/200 ) ]
SE = sqrt [0.003733] = 0.061
z = (p1 - p2) / SE = (0.38 - 0.51)/0.061 = -2.13
Suppose Acme Drug Company is making a new medicine designed to prevent colds. The company claims that the drug is equally effective for men and women. To test this claim, they chose a simple random sample of 100 women and 200 men from a population of 100,000 volunteers. At the end of the study, 38% of the women had a cold; and 51% of men caught a cold. Based on these results, can we rule out the company's claim that the drug is equally effective for men and women? Use a significance level of 0.05. Solution: The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results. We work through the following steps:
State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis. Null hypothesis: P1 = P2 Alternative hypothesis: P1 ≠ P2 Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the proportion of population 1 is too large or too small.
Formulate an analysis plan. For this analysis, the significance level is 0.05. The test method is a two-sided z-test.
Analyze the sample data. Using the sample data, we calculated the proportion of the pooled sample (p) and the standard error (SE). Using these measures, we compute the z-score (z) test statistic. The analysis described above is a two-proportion z-test.
Interpretation of results If the sample results are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P value with the significance level and rejecting the null hypothesis when the P value is less than the significance level. Hypothesis test: difference between proportions This lesson explains how to perform a hypothesis test to determine if the difference between two proportions is significant. The test procedure, called the two-sided z-test, is appropriate when the following conditions are met:
The sampling method for each population is a simple random sampling.
The samples are independent.
Each champion includes at least 10 successes and 10 failures.
Each population is at least 20 times larger than its sample.
This approach involves four phases: (1) declaring the hypotheses, (2) formulating an analysis plan, (3) analyzing the sample data, and (4) interpreting the results. State hypotheses Each hypothesis test requires the analyst to declare a null hypothesis and an alternative hypothesis. The following table shows three sets of hypotheses. Each makes a statement about the difference d between two proportions of the population, P1 and P2. (In the table, the symbol ≠ means "not equal to").
Set | Null hypothesis | Alternative hypothesis | Number of tails |
1 | P1 - P2 = 0 | P1 - P2 ≠ 0 | 2 |
2 | P1 - P2 > 0 | P1 - P2 < 0 | 1 |
3 | P1 - P2 < 0 | P1 - P2 > 0 | 1 |
- The first set of hypotheses (Set 1) is an example of a two-tailed test, since an extreme value on both sides of the sampling distribution would induce an investigator to reject the null hypothesis. The other two sets of hypotheses (sets 2 and 3) are one-tailed tests, since an extreme value on one side of the sampling distribution would induce an investigator to reject the null hypothesis.
- When the null hypothesis states that there is no difference between the two proportions of the population (i.e., d = P1 - P2 = 0), the null and alternative hypothesis for a two-tailed test is often stated as follows.
- I have: P1 = P2
- Has: P1 ≠ P2
- Formulate an analysis plan.
- The analysis plan describes how to use the sample data to accept or reject the null hypothesis. You must specify the following elements.
- Level of significance. Researchers often choose significance levels of 0.01, 0.05, or 0.10; but you can use any value between 0 and 1.
- Test method. Use the two aspect ratio z test (described in the next section) to determine if the assumed difference between population proportions differs significantly from the observed difference in the sample.
- Analyze the sample data.
- Using the sample data, complete the following calculations to find the test statistic and associated P-value.
- Proportion of the aggregate sample. Since the null hypothesis states that P1 = P2, we use an aggregate sample proportion (p) to calculate the standard error of the sampling distribution.
- p = (p1 * n1 + p2 * n2) / (n1 + n2)
- Where p1 is the proportion of the sample from population 1, p2 is the proportion of the sample from population 2, n1 is the size of sample 1 and n2 is the size of sample 2.
- Standard error. Calculate the standard error (SE) of the sampling distribution difference between two proportions.
- SE = sqrt {p * (1 - p) * [(1 / n1) + (1 / n2)]}
- Where p is the proportion of the pooled sample, n1 is the size of sample 1 and n2 is the size of sample 2.
- Statistical test. The test statistic is a z (z) score defined by the following equation.
- z = (p1 - p2) / SE
- Where p1 is the proportion of sample 1, p2 is the proportion of sample 2 and SE is the standard error of the sampling distribution.
- p-value The P value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a z-score, use the normal distribution calculator to assess the probability associated with the z-score. (See the example problems at the end of this lesson for examples of how this is done.)
- The analysis described above is a two-way z-test.
- Interpretation of results
- If the sample results are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P value with the significance level and rejecting the null hypothesis when the P value is less than the significance level.
- Test your understanding
- In this section, two sample problems illustrate how to perform a hypothesis test for the difference between two proportions. The first problem involves a two-tailed test; The second problem, a tail test.
- Problem 1: two-tailed test
- Suppose Acme Drug Company develops a new drug, designed to prevent colds. The company claims that the drug is equally effective for men and women. To test this claim, they chose a simple random sample of 100 women and 200 men from a population of 100,000 volunteers.
- At the end of the study, 38% of the women had a cold; and 51% of men caught a cold. Based on these results, can we rule out the company's claim that the drug is equally effective for men and women? Use a significance level of 0.05.
- Solution: The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results. We work through the following steps:
- State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis.
- Null hypothesis: P1 = P2
- Alternative hypothesis: P1 ≠ P2
- Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the proportion of population 1 is too large or too small.
- Formulate an analysis plan. For this analysis, the significance level is 0.05. The test method is a two-sided z-test.
- Analyze the sample data. Using the sample data, we calculated the proportion of the pooled sample (p) and the standard error (SE). Using these measures, we compute the z-score (z) test statistic.
- p = (p1 * n1 + p2 * n2) / (n1 + n2)
- p = [(0.38 * 100) + (0.51 * 200)] / (100 + 200)
- p = 140/300 = 0.467
- SE = sqrt {p * (1 - p) * [(1 / n1) + (1 / n2)]}
- SE = sqrt [0.467 * 0.533 * (1/100 + 1/200)]
- SE = sqrt [0.003733] = 0.061
- z = (p1 - p2) / SE = (0.38 - 0.51) /0.061 = -2.13
- Where p1 is the proportion of the sample in sample 1, where p2 is the proportion of the sample in sample 2, n1 is the size of sample 1 and n2 is the size of sample 2.
- Since we have a two-tailed test, the P value is the probability that the z-score is less than -2.13 or greater than 2.13.
- We use the normal distribution calculator to find P (z <-2.13) = 0.017 and P (z> 2.13) = 0.017. Therefore, the value P = 0.017 + 0.017 = 0.034.
- Interpret the results. Since the P value (0.034) is lower than the significance level (0.05), we cannot accept the null hypothesis.
- Note: If you use this approach during an exam, you can also mention why this approach is appropriate. In particular, the approach is appropriate because the sampling method was simple random sampling, the samples were independent, each population was at least 10 times larger than its sample, and each sample included at least 10 successes and 10 failures.
- Problem 2: testing a queue
- Suppose the previous example is declared slightly differently. Suppose Acme Drug Company develops a new drug, designed to prevent colds. The company claims that the drug is more effective for women than for men. To test this claim, they chose a simple random sample of 100 women and 200 men from a population of 100,000 volunteers.
- At the end of the study, 38% of the women had a cold; and 51% of men caught a cold. Based on these results, can we conclude that the medication is more effective for women than for men? Use a significance level of 0.01.
- Solution: The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results. We work through the following steps:
- State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis.
- Null hypothesis: P1> = P2
- Alternative hypothesis: P1 <P2
- Note that these hypotheses constitute a one-tailed test. The null hypothesis will be rejected if the percentage of women who have a cold (p1) is sufficiently lower than the proportion of men who have a cold (p2).
- Formulate an analysis plan. For this analysis, the significance level is 0.01. The test method is a two-sided z-test.
- Analyze the sample data. Using the sample data, we calculated the proportion of the pooled sample (p) and the standard error (SE). Using these measures, we compute the z-score (z) test statistic.
p = (p1 * n1 + p2 * n2) / (n1 + n2)
p = [(0.38 * 100) + (0.51 * 200)] / (100 + 200)
p = 140/300 = 0.467
SE = sqrt{ p * ( 1 - p ) * [ (1/n1) + (1/n2) ] }
SE = sqrt[ 0.467 * 0.533 * ( 1/100 + 1/200 ) ]
SE = sqrt [0.003733] = 0.061
z = (p1 - p2) / SE = (0.38 - 0.51)/0.061 = -2.13
Where p1 is the proportion of the sample in sample 1, where p2 is the proportion of the sample in sample 2, n1 is the size of sample 1 and n2 is the size of sample 2.
Subsequently we have a one-tailed test, the P significance is the probability that the z-score is less than -2.13. We practice the normal distribution calculator to discover P (z <-2.13) = 0.017. Therefore, the P value = 0.017.
Interpret the results. Since the P value (0.017) is greater than the significance level (0.01), we cannot reject the null hypothesis
5.2. Difference of proportions
To estimate the difference between two population proportions with a confidence interval, you can use the Central Limit Theorem when the sample sizes are large enough (typically, each at least 30). When a statistical characteristic, such as opinion on an issue (support/don’t support), of the two groups being compared is categorical, people want to report on the differences between the two population proportions — for example, the difference between the proportion of women and men who support a four-day work week. How do you do this?
You estimate the difference between two population proportions, p1 – p2, by taking a sample from each population and using the difference of the two sample proportions,
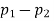
Plus or minus a margin of error. The result is called a confidence interval for the difference of two population proportions, p1 – p2.
The formula for a confidence interval (CI) for the difference between two population proportions is
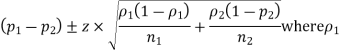
And n1 are the sample proportion and sample size of the first sample, and 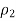

And n2 are the sample proportion and sample size of the second sample. The value z* is the appropriate value from the standard normal distribution for your desired confidence level. (Refer to the following table for z*-values.)
z*–values for Various Confidence Levels
Confidence Level | z*-value |
80% | 1.28 |
90% | 1.645 (by convention) |
95% | 1.96 |
98% | 2.33 |
99% | 2.58 |
To calculate a CI for the difference between two population proportions, do the following:
- Determine the confidence level and find the appropriate z*-value.
Refer to the above table.
2. Find the sample proportion
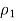
For the first sample by taking the total number from the first sample that are in the category of interest and dividing by the sample size, n1. Similarly, find 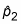 for the second sample.
for the second sample.
3. Take the difference between the sample proportions,
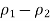
4. Find
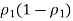
And divide that by n1. Find
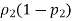
And divide that by n2. Add these two results together and take the square root.
5. Multiply z* times the result from Step 4.
This step gives you the margin of error.
6. Take
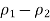
Plus or minus the margin of error from Step 5 to obtain the CI.
The lower end of the CI is
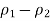
Minus the margin of error, and the upper end of the CI is
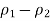
Plus the margin of error.
The formula shown here for a CI for p1 – p2 is used under the condition that both of the sample sizes are large enough for the Central Limit Theorem to be applied and allow you to use a z*-value; this is true when you are estimating proportions using large scale surveys, for example. For small sample sizes, confidence intervals are beyond the scope of an intro statistics course.
Suppose you work for the Las Vegas Chamber of Commerce, and you want to estimate with 95% confidence the difference between the percentage of all females who have ever gone to see an Elvis impersonator and the percentage of all males who have ever gone to see an Elvis impersonator, in order to help determine how you should market your entertainment offerings.
- Because you want a 95% confidence interval, your z*-value is 1.96.
- Suppose your random sample of 100 females includes 53 females who have seen an Elvis impersonator, so
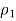
Is 53 divided by 100 = 0.53. Suppose also that your random sample of 110 males includes 37 males who have ever seen an Elvis impersonator, so
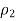
Is 37 divided by 110 = 0.34.
3. The difference between these sample proportions (females – males) is 0.53 – 0.34 = 0.19.
4. Take 0.53 ∗ (1 – 0.53) to obtain 0.2941. Then divide that by 100 to get 0.0025. Then take 0.34 ∗ (1 – 0.34) to obtain 0.2244. Then divide that by 110 to get 0.0020. Add these two results to get 0.0025 + 0.0020 = 0.0045. Then find the square root of 0.0045 which is 0.0671.
5. 1.96 ∗ 0.0671 gives you 0.13, or 13%, which is the margin of error.
6. Your 95% confidence interval for the difference between the percentage of females who have seen an Elvis impersonator and the percentage of males who have seen an Elvis impersonator is 0.19 or 19% (which you got in Step 3), plus or minus 13%. The lower end of the interval is 0.19 – 0.13 = 0.06 or 6%; the upper end is 0.19 + 0.13 = 0.32 or 32%.
To interpret these results within the context of the problem, you can say with 95% confidence that a higher percentage of females than males have seen an Elvis impersonator, and the difference in these percentages is somewhere between 6% and 32%, based on your sample.
The temptation is to say, “Well, I knew a greater proportion of women has seen an Elvis impersonator because that sample proportion was 0.53 and for men it was only 0.34. Why do I even need a confidence interval?” All those two numbers tell you is something about those 210 people sampled. You also need to factor in variation using the margin of error to be able to say something about the entire populations of men and women.
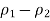
For example, if you had switched the males and females, you would have gotten –0.19 for this difference. That’s okay, but you can avoid negative differences in the sample proportions by having the group with the larger sample proportion serve as the first group (here, females).
However, even if the group with the larger sample proportion serves as the first group, sometimes you will still get negative values in the confidence interval. Suppose in the above example that only 0.43 of women had seen an Elvis impersonator. Thus, the difference in proportions is 0.09, and the upper end of the confidence interval is 0.09 + 0.13 = 0.22 while the lower end is 0.09 – 0.13 = –0.04. This means that the true difference is reasonably anywhere from 22% more women to 4% more men. It’s too close to tell for sure.
5.3. Single mean, Difference of means and difference of standard deviations
The single mean (or one-sample) t-test is used to compare the mean of a variable in a sample of data to a (hypothesized) mean in the population from which our sample data are drawn. This is important because we seldom have access to data for an entire population. The hypothesized value in the population is specified in the Comparison value box.
We can perform either a one-sided test (i.e., less than or greater than) or a two-sided test (see the Alternative hypothesis dropdown). We use one-sided tests to evaluate if the available data provide evidence that the sample mean is larger (or smaller) than the comparison value (i.e., the population value in the null-hypothesis)
Example :
We have access to data from a random sample of grocery stores in the UK. Management will consider entering this market if consumer demand for the product category exceeds 100M units, or, approximately, 1750 units per store. The average demand per store in the sample is equal to 1953. While this number is larger than 1750 we need to determine if the difference could be attributed to sampling error.
You can find the information on unit sales in each of the sample stores in the demand_uk.rda data set. The data set contains two variables, store_id and demand_uk. Our null-hypothesis is that the average store demand in the UK is equal to 1750 unit so we enter that number into the Comparison value box. We choose the Greater than option from the Alternative hypothesis drop-down because we want to determine if the available data provides sufficient evidence to reject the null-hypothesis favor of the alternative that average store demand in the UK is larger than 1750.
The first two blocks of output show basic information about the test (e.g.,. The null and alternative hypothesis) and summary statistics (e.g., mean, standard deviation, standard error, margin or error, etc.). The final row of output shows the following:
- Diff is the difference between the sample mean (1953.393) and the comparison value (1750)
- Se is the standard error (i.e., the standard deviation of the sampling distribution of diff)
- t.value is the t statistic associated with diff that we can compare to a t-distribution (i.e., diff / se)
- p.value is the probability of finding a value as extreme or more extreme than diff if the null hypothesis is true
- Df is the degrees of freedom associated with the statistical test (i.e., n - 1)
- 5% 100% show the 95% confidence interval around the sample mean (1897 to Inf.). These numbers provide a range within which the true population mean is likely to fall
Significance test of difference between sample means
Given two independent examples 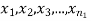 and
and 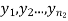 with means
with means 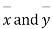 standard derivations
standard derivations 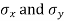 from a normal population with the same variance, we have to test the hypothesis that the population means
from a normal population with the same variance, we have to test the hypothesis that the population means 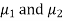 are same For this, we calculate
are same For this, we calculate
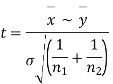
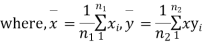
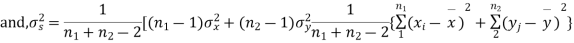
It can be shown that the variate t defined by (1) follows the t distribution with 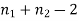 degrees of freedom.
degrees of freedom.
If the calculated value 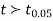 the difference between the sample means is said to be significant at 5% level of significance.
the difference between the sample means is said to be significant at 5% level of significance.
If 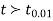 , the difference is said to be significant at 1% level of significance.
, the difference is said to be significant at 1% level of significance.
If 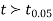 the data is said to be consistent with the hypothesis that
the data is said to be consistent with the hypothesis that 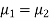 .
.
Cor. If the two samples are of same size and the data are paired, then t is defined by
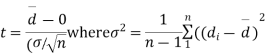
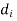 =difference of the ith member of the sample
=difference of the ith member of the sample
d=mean of the differences =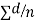 and the member of d.f.=n-1.
and the member of d.f.=n-1.
Example Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
Sol. We compute the mean and the S.D. Of the difference between the marks of the two tests as under:
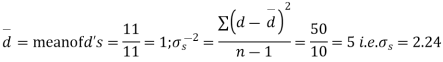
Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.
Then, 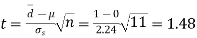 nearly and df v=11-1=10
nearly and df v=11-1=10
Students | 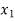 | 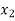 | 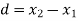 | 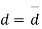 | 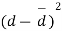 |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
| 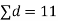 |
| 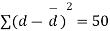 |
- From table IV, we find that
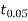 (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of 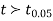 , the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
Example:
- From a random sample of 10 pigs fed on diet A, the increase in weight in certain period were 10,6,16,17,13,12,8,14,15,9 lbs. For another random sample of 12 pigs fed on diet B, the increase in the same period were 7,13,22,15,12,14,18,8,21,23,10,17 lbs. Test whether diets A and B differ significantly as regards their effect on increases in weight ?
- Sol. We calculate the means and standard derivations of the samples as follows
| Diet A |
|
| Diet B |
|
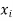 | 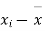 | 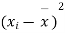 | 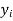 | 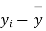 | 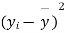 |
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 13 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 17 | 2 | 4 |
|
|
|
|
|
|
120 |
|
| 180 | 0 | 314 |
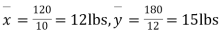
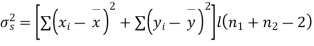
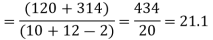
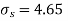
Assuming that the samples do not differ in weight so far as the two diets are concerned i.e. 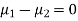
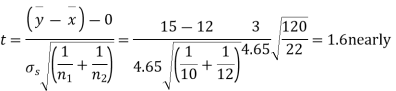
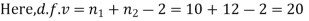
For v=20, we find 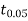 =2.09
=2.09
The calculated value of 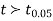
Hence the difference between the samples means is not significant i.e. thew two diets do not differ significantly as regards their effects on increase in weight.
Module-6
Small samples
6.1. Test for single mean
When you test a single mean, you’re comparing the mean value to some other hypothesized value. Which test you run depends on if you know the population standard deviation (σ) or not.
Known population standard deviation
If you know the value for σ, then the population mean has a normal distribution: use a one sample z-test. The z-test uses a formula to find a z-score, which you compare against a critical value found in a z-table. The formula is:
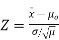
A one sample test of means compares the mean of a sample to a pre-specified value and tests for a deviation from that value. For example we might know that the average birth weight for white babies in the US is 3,410 grams and wish to compare the average birth weight of a sample of black babies to this value.
Assumptions
- Independent observations.
- The population from which the data is sampled is normally distributed.
Hypothesis:
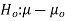
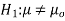
Where μ0 is a pre-specified value (in our case this would be 3,410 grams).
Test Statistic
- First calculate
 , the sample mean.
, the sample mean. - We choose an α = 0.05 significance level
- If the standard deviation is known:
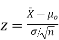
Using the significance level of 0.05, we reject the null hypothesis if z is greater than 1.96 or less than -1.96.
- If the standard deviation is unknown:
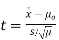
Using the significance level of 0.05, we reject the null hypothesis if |t| is greater than the critical value from a t-distribution with df = n-1.
Note: The shaded area is referred to as the critical region or rejection region.
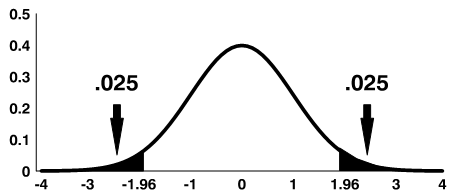
We can also calculate a 95% confidence interval around the mean. The general form for a confidence interval around the mean, if σ is unknown, is
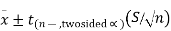
For a two-sided 95% confidence interval, use the table of the t-distribution (found at the end of the section) to select the appropriate critical value of t for the two-sided α=0.05.
Example: one sample t-test
Recall the data used in module 3 in the data file "dixonmassey."
Data dixonmassey;
Input Obs chol52 chol62 age cor dchol agelt50 $;
Datalines;
1 | 240 | 209 | 35 | 0 | -31 | y |
2 | 243 | 209 | 64 | 1 | -34 | n |
3 | 250 | 173 | 61 | 0 | -77 | n |
4 | 254 | 165 | 44 | 0 | -89 | y |
5 | 264 | 239 | 30 | 0 | -25 | y |
6 | 279 | 270 | 41 | 0 | -9 | y |
7 | 284 | 274 | 31 | 0 | -10 | y |
8 | 285 | 254 | 48 | 1 | -31 | y |
9 | 290 | 223 | 35 | 0 | -67 | y |
10 | 298 | 209 | 44 | 0 | -89 | y |
11 | 302 | 219 | 51 | 1 | -83 | n |
12 | 310 | 281 | 52 | 0 | -29 | n |
13 | 312 | 251 | 37 | 1 | -61 | y |
14 | 315 | 208 | 61 | 1 | -107 | n |
15 | 322 | 227 | 44 | 1 | -95 | y |
16 | 337 | 269 | 52 | 0 | -68 | n |
17 | 348 | 299 | 31 | 0 | -49 | y |
18 | 384 | 238 | 58 | 0 | =146 | n |
19 | 386 | 285 | 33 | 0 | -101 | y |
20 | 520 | 325 | 40 | 1 | -195 | y |
;
Many doctors recommend having a total cholesterol level below 200 mg/dl. We will test to see if the 1952 population from which the Dixon and Massey sample was gathered is statistically different, on average, from this recommended level.
- H0: μ = 200 vs. H1: μ ≠ 200
- α=0.05
- Our sample of n=20 has
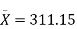 = 311.15 and s = 64.3929.
= 311.15 and s = 64.3929. - Df = 19, so reject H0 if |t| > 2.093
Calculate:
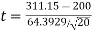
|t| > 2.093 so we reject H0
The 95% confidence limits around the mean are
311.15 ± (2.093)(64.3929/√20)
311.15 ± 30.14
(281.01, 341.29)
One Sample t-test Using SAS:
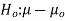
Proc ttest data=name h0=μ0 alpha=α;
Var var;
Run;
SAS uses the stated α for the level of confidence (for example, α=0.05 will result in 95% confidence limits). For the hypothesis test, however, it does not compute critical values associated with the given α, and compare the t-statistic to the critical value. Rather, SAS will provide the p-value, the probability that T is more extreme than observed t. The decision rule, "reject if |t| > critical value associated with α" is equivalent to "reject if p < α."
SAS will provide the p value, the probability that T is more extreme than observed t. The decision rule, “reject if |t| critical value associated with
critical value associated with 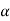 ” is equivalent to “reject if p
” is equivalent to “reject if p  a.”
a.”
Example:
Proc ttest data=dixonmassey h0=200 alpha=0.05;
Var chol52;
Title 'One Sample t-test with proc ttest';
Title2 'Testing if the sample of cholesterol levels in 1952 is statistically different from 200' ;
Run;
One sample t-test with proc ttest
‘Testing if the sample of cholesterol level in 1952 is statistically different from
The T TEST Procedure
Variable : chol52
N | Mean | Std Dev | Std Err | Minimum | Maximum |
20 | 311.2 | 64.3929 | 14.3987 | 240.0 | 520.0 |
Mean | 95% CL Mean | Std Dev | 95% CL | Std Dev |
311.2 | 281.0 | 64.3929 | 48.9702 | 94.0505 |
DF | T Value | Pr> |t| |
19 | 7.72 | <.0001 |
As in our hand calculations, t = 7.72, and we reject H0 (because p<0.0001 which is < 0.05, our selected α level).
The mean cholesterol in 1952 was 311.2, with 95% confidence limits (281.0, 341.3).
6.2. Difference for means and correlations coefficients
Testing the meaning of the correlation coefficient.
The relationship coefficient, r, tells us about the strength and direction of the linear relationship between X1 and X2.
Sample data is used to calculate r, the correlation coefficient for the sample. If we had data for the entire population, we could find the correlation coefficient for the population.
But since we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r, is our estimate of the correlation coefficient for the unknown population.
• ρ = population correlation coefficient (unknown)
• r = sample relationship coefficient (known; calculated from sample data)
The hypothesis test allows us to decide if the value of the population correlation coefficient ρ is "close to zero" or "significantly different from zero". We decide on the basis of the correlation coefficient of sample r and the size of sample n.
If the test arranges that the relationship coefficient is meaningfully different from zero, we say that the relationship coefficient is "significant".
• Conclusion: there is sufficient evidence to conclude that there is a significant linear relationship between X1 and X2 because the correlation coefficient is significantly different from zero.
• Meaning of the conclusion: there is a significant linear relationship X1 and X2. If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that the correlation coefficient is not "significant".
Take the hypothesis test
• Null hypothesis: H0: ρ = 0
• Alternative hypothesis: Ha: ρ≠ 0
What do hypotheses mean in words?
• Hypothesis H0: the population correlation coefficient is NOT meaningfully dissimilar from zero. There is NO significant linear relationship (correlation) between X1 and X2 in the population.
• Alternative hypothesis Ha: the population correlation coefficient is significantly different from zero. Here is a significant linear relationship (correlation) amid X1 and X2 in the population.
Drawing a conclusion There are two methods of making a hypothetical decision. The test statistic to test this hypothesis is:
When the second formula is an equivalent form of the test statistic, n is the sample size and the degrees of freedom are n-2. This is a t-statistic and works in the same way as other t-tests.
Calculate the value t and compare it to the critical value in table t at the appropriate degrees of freedom and the level of confidence you want to maintain. If the calculated value is in the queue, then you cannot accept the null hypothesis that there is no linear relationship between these two independent random variables.
If the calculated t value is NOT in the queue, it is not possible to reject the null hypothesis that there is no linear relationship between the two variables.
A quick way to test correlations is the relationship between sample size and correlation. Me:
Then this implies that the correlation between the two variables demonstrates the existence of a linear relationship and is statistically significant at approximately the significance level of 0.05.
As the formula indicates, there is an inverse relationship between the sample size and the required correlation for the meaning of a linear relationship.
With only 10 observations, the required correlation for significance is 0.6325, for 30 observations the required correlation for significance drops to 0.3651 and for 100 observations the required level is only 0.2000.
Correlations can be useful for visualizing data, but are not used appropriately to "explain" a relationship between two variables. Perhaps a single statistic is not used more inadequately than the correlation coefficient.
Quoting correlations between health conditions and anything from place of residence to eye color has the effect of implying a cause and effect relationship. This simply cannot be accomplished with a correlation coefficient.
The correlation coefficient is obviously innocent of this misinterpretation. The analyst has a duty to use a statistic designed to test cause and effect relationships and report those results only if he intends to submit such a request.
The problem is that passing this stricter test is difficult, so lazy and / or unscrupulous "investigators" turn to correlations when they cannot legitimately support their case.
Define a t-test of a regression coefficient and provide a unique example of its use. Definition: A t-test is obtained by dividing a regression coefficient by its standard error and then comparing the result with critical values for students with df error.
Provides a test for the claim that when all other variables were included in the relevant regression model. Example: Suppose that 4 variables are suspected to influence some response. Suppose the assembly results include:
Variable | Regression coefficient | Standard error of regular coefficient |
.5 | 1 | -3 |
.4 | 2 | +2 |
.02 | 3 | +1 |
.6 | 4 | -.5 |
- t calculated for variables 1, 2 and 3 would be 5 or greater in absolute value while for variable 4 it would be less than 1. For most levels of significance, the hypothesis would be rejected. However, note that this is the case where, and have been included in the regression. For most levels of significance, the hypothesis would have continued (held) for the case where, and are in regression. Often this pattern of results will involve calculating another regression involving only and examining the proportions produced for that case.
- The correlation between the scores on a neuroticism test and the scores on an anxiety test is high and positive; Thus
- To. Anxiety causes neuroticism
- Yes. Those who score low on one test tend to score high on the other.
- C. Those who score small on one test tend to score low on the other.
- Re. You cannot make a meaningful prediction from one test to another.
- C. Those who score small on one test tend to score low on the additional.
- Testing the meaning of the correlation coefficient.
- LEARNING OUTCOMES
- • Calculate and interpret the correlation coefficient.
- The correlation coefficient, r, says us about the asset and direction of the linear relationship amid x and y. However, the reliability of the linear model also depends on the number of data points observed in the sample. We have to examine together the value of the correlation coefficient r and the sample size n.
- We done a hypothesis test on the "significance of the correlation coefficient" to choose whether the linear relationship in the sample data is strong sufficient to be used to model the connection in the population.
- Sample data is used to calculate r, the correlation coefficient for the sample. If we had data for the entire population, we could find the correlation coefficient for the population. But since we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r, is our estimate of the correlation coefficient for the unknown population.
- • The representation for the population correlation coefficient is ρ, the Greek letter "rho".
- ρ = population correlation coefficient (unknown)
- r = sample correlation coefficient (known; calculated from sample data)
- The hypothesis test allows us to decide if the value of the population correlation coefficient
- ρ is "near to zero" or "significantly dissimilar from zero". We decide on the basis of the correlation coefficient of sample r and the size of sample n.
- If the test determines that the correlation coefficient is meaningfully dissimilar from zero, we say that the association coefficient is "significant".
- Assumption: there is sufficient indication to accomplish that there is a important linear relationship between x and y, since the association coefficient is significantly dissimilar from zero. What does the conclusion mean: There is a significant linear relationship between x and y. We can practice the reversion line to model the linear relationship amid x and y in the population.
- If the test achieves that the correlation coefficient is not meaningfully diverse from zero (it is close to zero), we say that the correlation coefficient is not "significant".
- Assumption: “There is insufficient indication to accomplish that there is a significant linear relationship amid
- x and y because the correlation coefficient is not meaningfully dissimilar from zero. "What the conclusion means: There is no important linear association between x and y. So, we CANNOT use the reversion line to model a linear relationship amid x and y in the population.
- Note
- • If r is significant and the scatter diagram shows a linear trend, the line can be used to predict the value of y for the values of x that fall within the domain of the observed values of x.
- • If r is not significant OR if the scatter diagram does not show a linear trend, the line should not be used for forecasting.
- • If r is significant and if the scatter diagram shows a linear trend, the line may NOT be appropriate or reliable to predict OUT of the domain of the x values observed in the data.
- Take the hypothesis test
- Null hypothesis: H0: ρ = 0
- Alternative hypothesis: Ha: ρ≠ 0
- What do hypotheses mean in words?
- Hypothesis H0: the population relationship coefficient is NOT meaningfully dissimilar from zero. There is NO significant linear relationship (correlation) between x and y in the population.
- Alternative hypothesis Ha: the population correlation coefficient is significantly different from zero. There is a important linear relationship (correlation) between x and y in the population.
- Get a conclusion
- There are two methods of making the decision. The two methods are equivalent and give the same result.
- Method 1: using the p value
- Method 2: use of a table of critical values.
- In this chapter of this textbook, we will continuously use a significance level of 5%, α = 0.05
Note
- Using the p-value method, you can choose any appropriate level of significance desired; It is not limited to the use of α = 0.05. But the critical value table provided in this textbook assumes that we are using a significance level of 5%, α = 0.05. (If we wanted to use a significance level other than 5% with the critical value method, we would need several tables of critical values that are not provided in this manual).
- Method 1: use a p-value to make a decision
- To calculate the p-value using LinRegTTEST:
- • On the LinRegTTEST input screen, at the line prompt for β or ρ, highlight "≠ 0"
- The output screen shows the p value on the line that says "p =".
- (Most statistical software can calculate the p-value).
- If the p value is fewer than the meaning level (α = 0.05)
- Decision: reject the null hypothesis.
- Assumption: "There is sufficient indication to accomplish that there is aimportant linear relationship amid x and y since the correlation coefficient is meaningfullydissimilar from zero."
- If the p value is NOT less than the meaning level (α = 0.05)
- Decision: DO NOT reject the null hypothesis.
- Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between x and y because the correlation coefficient is NOT significantly different from zero."
- Calculation Notes:
- Use technology to calculate the p-value. The calculations for calculating test statistics and p-value are described below:
- The p-value is considered using a t-distribution with n - 2 degrees of freedom.
- The formula for the test statistic is t = r√n - 2√1 - r2t = rn - 21 - r2. The test statistic value, t, is displayed on the computer or calculator output along with the p-value. The t-test statistic has the same sign as the correlation coefficient r.
- The p-value is the combined area in both tails.
6.3. Test for ratio of variances: Chi-square test for goodness of fit and independent of attributes.
Chi-square test for independence
This lesson explains how to take a chi-square test for independence. The test is useful when you have two definite variables from a single population.
It is used to determine if there is a significant association between the two variables.
For example, in an electoral poll, voters could be classified by gender (male or female) and voting preference (democratic, republican, or independent).
We could use a chi-square test for independence to determine if gender is linked to voting preference. The example problem at the end of the lesson considers this example.
When to use the Chi-square test for independence
The testing procedure described in this lesson is appropriate when the following conditions are true:
The sample method is a simple random sampling.
The variables under consideration are categorical.
If the sample data is showed in a likelihood table, the predictable frequency total for each cell in the table is at least 5.
This approach involves four phases: (1) declaring the hypotheses, (2) formulating an analysis plan, (3) analyzing the sample data, and (4) interpreting the results.
State hypotheses
Suppose that variable A has levels r and that variable B has levels c. The null hypothesis establishes that knowing the level of variable A does not help to predict the level of variable B.
That is, the variables are independent.
Ho: variable A and variable B are independent.
Ha: variables A and B are not independent.
The another hypothesis is that meaningful the level of flexible A can help you expect the level of variable B.
Note: support for the another hypothesis proposes that the variables are connected; but the connection is not essentially connecting, in the sense that one variable "causes" the other.
Formulate an analysis plan.
The analysis plan describes how to use the sample data to accept or reject the null hypothesis. The plan must specify the following elements.
Level of significance. Researchers often choose significance levels of 0.01, 0.05, or 0.10; but you can use any value between 0 and 1.
Test method. Use the chi-square test to determine independence to determine if there is a significant relationship between two categorical variables.
Analyze the sample data.
Using the sample data, find the degrees of freedom, the predictable frequencies, the test statistic, and the P value associated with the test statistic. The method defined in this unit is showed in the sample problematic at the end of this lesson.
Degrees of freedom. The degrees of freedom (DF) are equal to:
DF = (r - 1) * (c - 1)
Where r is the number of levels for one catabolic variable and c is the number of levels for the other categorical variable.
You predictable frequencies. The predictable frequency counts are considered distinctly for each level of one definite variable at each level of the other categorical variable.
Calculate the predictable frequencies r * c, according to the following formula.
Er, c = (nr * nc) / n
Where Er, c is the predictable frequency count for level r of variable A and level c of variable B, nr is the total number of sample explanations at level r of variable A, nc is the total number of sample explanations at level c of variable B, en is the total sample size.
Statistical test. The test statistic is a chi-square (Χ2) random variable defined by the following equation.
Χ2 = Σ[ (Or,c - Er,c)2 / Er,c ]
Where O, c is the observed frequency count at level r of variable A and level c of variable B, and Er, c is the predicted frequency count at level r of adjustable A and level c of adjustable B.
p-value The P value is the probability of detecting a sample figure as exciting as the test statistic.
Meanwhile the test measurement is a chi-square, use the Chi-square supply calculator to measure the probability related with the test statistic. Use the degrees of freedom considered above.
Interpretation of results
If the sample results are unlikely, given the null hypothesis, the researcher rejects the null hypothesis.
Typically, this involves comparing the P value with the significance level and rejecting the null hypothesis when the P value is less than the significance level.
Test your understanding:
A public opinion poll analyzed a simple random sample of 1,000 voters. Respondents were classified by gender (male or female) and by voting preference (Republican, Democratic, or Independent).
The effects are shown in the possibility table below.
| Voting Preferences | Row total | ||
Rep | Dem | Ind | ||
Male | 200 | 150 | 50 | 400 |
Female | 250 | 300 | 50 | 600 |
Column total | 450 | 450 | 100 | 1000 |
- Is there a gender gap? Do men's voting preferences differ significantly from women's preferences? Use a significance level of 0.05. Solution The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results.
- We work through the following steps:
State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis. Ho: Gender and voting preferences are independent. Ha: Gender and voting preferences are not independent.
Formulate an analysis plan. For this analysis, the significance level is 0.05. Using sample data, we will perform a chi-square test for independence.
Analyze the sample data. By applying the chi-square test for independence to the sampling data, we calculated degrees of freedom, predictable frequency counts, and chi-square test statistics.
Based on the chi-square statistic and the degrees of freedom, we determine the value P..
DF = (r - 1) * (c - 1) = (2 - 1) * (3 - 1) = 2
Er,c = (nr * nc) / n
E1,1 = (400 * 450) / 1000 = 180000/1000 = 180
E1,2 = (400 * 450) / 1000 = 180000/1000 = 180
E1,3 = (400 * 100) / 1000 = 40000/1000 = 40
E2,1 = (600 * 450) / 1000 = 270000/1000 = 270
E2,2 = (600 * 450) / 1000 = 270000/1000 = 270
E2,3 = (600 * 100) / 1000 = 60000/1000 = 60
Χ2 = Σ [ (Or,c - Er,c)2 / Er,c ]
Χ2 = (200 - 180)2/180 + (150 - 180)2/180 + (50 - 40)2/40
+ (250 - 270)2/270 + (300 - 270)2/270 + (50 - 60)2/60
Χ2 = 400/180 + 900/180 + 100/40 + 400/270 + 900/270 + 100/60
Χ2 = 2.22 + 5.00 + 2.50 + 1.48 + 3.33 + 1.67 = 16.2
Where DF is the degree of freedom, r is the number of levels of gender, c is the number of levels of the voting preference, nr is the number of observations of level r of gender, nc is the number of observations of level c of voting preference, n is the number of observations in the sample, Er, c is the predicted frequency count when gender is level r and voting preference is level c, and O, c is the observed frequency count when gender is level r, voting preference is level c.
The P value is the probability that a chi-square statistic with 2 degrees of freedom is more extreme than 16.2.
We use the Chi-Square distribution calculator to find P (Χ2> 16.2) = 0.0003.
Interpret the results. Since the P value (0.0003) is lower than the significance level (0.05), we cannot accept the null hypothesis.
Therefore, we conclude that there is a relationship between gender and voting preference.