UNIT- 3

Function

3.1 Function, Functions (including using built in libraries)

In c, we can divide a large program into the basic building blocks known as function. The function contains the set of programming statements enclosed by {}. A function can be called multiple times to provide reusability and modularity to the C program. In other words, we can say that the collection of functions creates a program. The function is also known as procedureor subroutinein other programming languages.

Advantage of functions in C

There are the following advantages of C functions.

• By using functions, we can avoid rewriting same logic/code again and again in a program.
• We can call C functions any number of times in a program and from any place in a program.
• We can track a large C program easily when it is divided into multiple functions.
• Reusability is the main achievement of C functions.
• However, Function calling is always a overhead in a C program.

Function Aspects

There are three aspects of a C function.

• Function declaration A function must be declared globally in a c program to tell the compiler about the function name, function parameters, and return type.

• Function call Function can be called from anywhere in the program. The parameter list must not differ in function calling and function declaration. We must pass the same number of functions as it is declared in the function declaration.

• Function definition It contains the actual statements which are to be executed. It is the most important aspect to which the control comes when the function is called. Here, we must notice that only one value can be returned from the function.

The syntax of creating function in c language is given below:

1. Return_type function_name(data_type parameter...){  
2. //code to be executed  
3. }  

Types of Functions

There are two types of functions in C programming:

1. Library Functions: are the functions which are declared in the C header files such as scanf(), printf(), gets(), puts(), ceil(), floor() etc.
2. User-defined functions: are the functions which are created by the C programmer, so that he/she can use it many times. It reduces the complexity of a big program and optimizes the code.

Return Value

A C function may or may not return a value from the function. If you don't have to return any value from the function, use void for the return type.

Let's see a simple example of C function that doesn't return any value from the function.

Example without return value:

1. Void hello(){  
2. Printf("hello c");  
3. }  

If you want to return any value from the function, you need to use any data type such as int, long, char, etc. The return type depends on the value to be returned from the function.

Let's see a simple example of C function that returns int value from the function.

Example with return value:

1. Int get(){  
2. Return 10;  
3. }  

In the above example, we have to return 10 as a value, so the return type is int. If you want to return floating-point value (e.g., 10.2, 3.1, 54.5, etc), you need to use float as the return type of the method.

1. Float get(){  
2. Return 10.2;  
3. }  

Now, you need to call the function, to get the value of the function.

Different aspects of function calling

A function may or may not accept any argument. It may or may not return any value. Based on these facts, There are four different aspects of function calls.

• Function without arguments and without return value
• Function without arguments and with return value
• Function with arguments and without return value
• Function with arguments and with return value

Example for Function without argument and return value

Example 1

1. #include<stdio.h>  
2. Void printName();  
3. Void main ()  
4. {  
5.    Printf("Hello ");  
6.    PrintName();  
7. }  
8. Void printName()  
9. {  
10.    Printf("Javatpoint");  
11. }  

Output

Hello Javatpoint

Example 2

1. #include<stdio.h>  
2. Void sum();  
3. Void main()  
4. {  
5.    Printf("\nGoing to calculate the sum of two numbers:");  
6.    Sum();  
7. }  
8. Void sum()  
9. {  
10.    Int a,b;   
11.    Printf("\nEnter two numbers");  
12.    Scanf("%d %d",&a,&b);   
13.    Printf("The sum is %d",a+b);  
14. }  

Output

Going to calculate the sum of two numbers:

Enter two numbers 10

24

The sum is 34

Example for Function without argument and with return value

Example 1

1. #include<stdio.h>  
2. Int sum();  
3. Void main()  
4. {  
5.    Int result;   
6.    Printf("\nGoing to calculate the sum of two numbers:");  
7.    Result = sum();  
8.    Printf("%d",result);  
9. }  
10. Int sum()  
11. {  
12.    Int a,b;   
13.    Printf("\nEnter two numbers");  
14.    Scanf("%d %d",&a,&b);  
15.    Return a+b;   
16. }  

Output

Going to calculate the sum of two numbers:

Enter two numbers 10

24

The sum is 34

Example 2: program to calculate the area of the square

1. #include<stdio.h>  
2. Int sum();  
3. Void main()  
4. {  
5.    Printf("Going to calculate the area of the square\n");  
6.    Float area = square();  
7.    Printf("The area of the square: %f\n",area);  
8. }  
9. Int square()  
10. {  
11.    Float side;  
12.    Printf("Enter the length of the side in meters: ");  
13.    Scanf("%f",&side);  
14.    Return side * side;  
15. }  

Output

Going to calculate the area of the square

Enter the length of the side in meters: 10

The area of the square: 100.000000

Example for Function with argument and without return value

Example 1

1. #include<stdio.h>  
2. Void sum(int, int);  
3. Void main()  
4. {  
5.    Int a,b,result;   
6.    Printf("\nGoing to calculate the sum of two numbers:");  
7.    Printf("\nEnter two numbers:");  
8.    Scanf("%d %d",&a,&b);  
9.    Sum(a,b);  
10. }  
11. Void sum(int a, int b)  
12. {  
13.    Printf("\nThe sum is %d",a+b);      
14. }  

Output

Going to calculate the sum of two numbers:

Enter two numbers 10

24

The sum is 34

Example 2: program to calculate the average of five numbers.

1. #include<stdio.h>  
2. Void average(int, int, int, int, int);  
3. Void main()  
4. {  
5.    Int a,b,c,d,e;   
6.    Printf("\nGoing to calculate the average of five numbers:");  
7.    Printf("\nEnter five numbers:");  
8.    Scanf("%d %d %d %d %d",&a,&b,&c,&d,&e);  
9.    Average(a,b,c,d,e);  
10. }  
11. Void average(int a, int b, int c, int d, int e)  
12. {  
13.    Float avg;   
14.    Avg = (a+b+c+d+e)/5;   
15.    Printf("The average of given five numbers : %f",avg);  
16. }  

Output

Going to calculate the average of five numbers:

Enter five numbers:10

20

30

40

50

The average of given five numbers : 30.000000

Example for Function with argument and with return value

Example 1

1. #include<stdio.h>  
2. Int sum(int, int);  
3. Void main()  
4. {  
5.    Int a,b,result;   
6.    Printf("\nGoing to calculate the sum of two numbers:");  
7.    Printf("\nEnter two numbers:");  
8.    Scanf("%d %d",&a,&b);  
9.    Result = sum(a,b);  
10.    Printf("\nThe sum is : %d",result);  
11. }  
12. Int sum(int a, int b)  
13. {  
14.    Return a+b;  
15. }  

Output

Going to calculate the sum of two numbers:

Enter two numbers:10

20

The sum is : 30  

Example 2: Program to check whether a number is even or odd

1. #include<stdio.h>  
2. Int even_odd(int);  
3. Void main()  
4. {  
5. Int n,flag=0;  
6. Printf("\nGoing to check whether a number is even or odd");  
7. Printf("\nEnter the number: ");  
8. Scanf("%d",&n);  
9. Flag = even_odd(n);  
10. If(flag == 0)  
11. {  
12.    Printf("\nThe number is odd");  
13. }  
14. Else   
15. {  
16.    Printf("\nThe number is even");  
17. }  
18. }  
19. Int even_odd(int n)  
20. {  
21.    If(n%2 == 0)  
22.    {  
23.        Return 1;  
24.    }  
25.    Else   
26.    {  
27.        Return 0;  
28.    }  
29. }  

Output

Going to check whether a number is even or odd

Enter the number: 100

The number is even

C Library Functions

Library functions are the inbuilt function in C that are grouped and placed at a common place called the library. Such functions are used to perform some specific operations. For example, printf is a library function used to print on the console. The library functions are created by the designers of compilers. All C standard library functions are defined inside the different header files saved with the extension .h. We need to include these header files in our program to make use of the library functions defined in such header files. For example, To use the library functions such as printf/scanf we need to include stdio.h in our program which is a header file that contains all the library functions regarding standard input/output.

The list of mostly used header files is given in the following table.

3.2 Parameter passing in functions, Call by value, idea of call by reference

There are two methods to pass the data into the function in C language, i.e., call by value and call by reference.

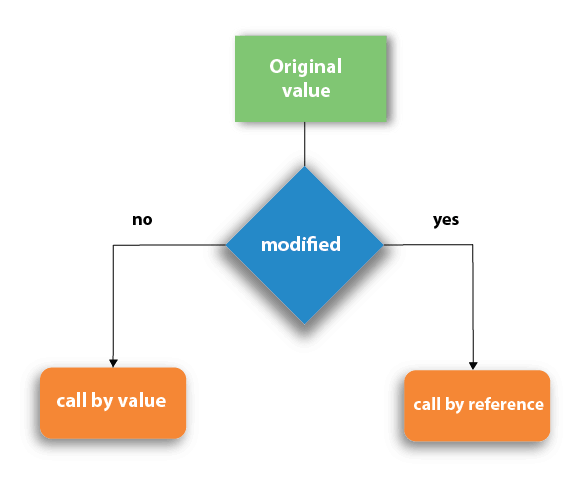
Let's understand call by value and call by reference in c language one by one.

Call by value in C

• In call by value method, the value of the actual parameters is copied into the formal parameters. In other words, we can say that the value of the variable is used in the function call in the call by value method.
• In call by value method, we cannot modify the value of the actual parameter by the formal parameter.
• In call by value, different memory is allocated for actual and formal parameters since the value of the actual parameter is copied into the formal parameter.
• The actual parameter is the argument which is used in the function call whereas formal parameter is the argument which is used in the function definition.

Let's try to understand the concept of call by value in c language by the example given below:

1. #include<stdio.h>  
2. Void change(int num) {    
3.    Printf("Before adding value inside function num=%d \n",num);    
4.    Num=num+100;    
5.    Printf("After adding value inside function num=%d \n", num);    
6. }    
7. Int main() {    
8.    Int x=100;    
9.    Printf("Before function call x=%d \n", x);    
10.    Change(x);//passing value in function    
11.    Printf("After function call x=%d \n", x);    
12. Return 0;  
13. }    

Output

Before function call x=100

Before adding value inside function num=100

After adding value inside function num=200

After function call x=100

Call by Value Example: Swapping the values of the two variables

1. #include <stdio.h>  
2. Void swap(int , int); //prototype of the function   
3. Int main()  
4. {  
5.    Int a = 10;  
6.    Int b = 20;   
7.    Printf("Before swapping the values in main a = %d, b = %d\n",a,b); // printing the value of a and b in main  
8.    Swap(a,b);  
9.    Printf("After swapping values in main a = %d, b = %d\n",a,b); // The value of actual parameters do not change by changing the formal parameters in call by value, a = 10, b = 20  
10. }  
11. Void swap (int a, int b)  
12. {  
13.    Int temp;   
14.    Temp = a;  
15.    a=b;  
16.    b=temp;  
17.    Printf("After swapping values in function a = %d, b = %d\n",a,b); // Formal parameters, a = 20, b = 10   
18. }  

Output

Before swapping the values in main a = 10, b = 20

After swapping values in function a = 20, b = 10

After swapping values in main a = 10, b = 20 

Call by reference in C

• In call by reference, the address of the variable is passed into the function call as the actual parameter.
• The value of the actual parameters can be modified by changing the formal parameters since the address of the actual parameters is passed.
• In call by reference, the memory allocation is similar for both formal parameters and actual parameters. All the operations in the function are performed on the value stored at the address of the actual parameters, and the modified value gets stored at the same address.

Consider the following example for the call by reference.

1. #include<stdio.h>  
2. Void change(int *num) {    
3.    Printf("Before adding value inside function num=%d \n",*num);    
4.    (*num) += 100;    
5.    Printf("After adding value inside function num=%d \n", *num);    
6. }      
7. Int main() {    
8.    Int x=100;    
9.    Printf("Before function call x=%d \n", x);    
10.    Change(&x);//passing reference in function    
11.    Printf("After function call x=%d \n", x);    
12. Return 0;  
13. }    

Output

Before function call x=100

Before adding value inside function num=100

After adding value inside function num=200

After function call x=200

Call by reference Example: Swapping the values of the two variables

1. #include <stdio.h>  
2. Void swap(int *, int *); //prototype of the function   
3. Int main()  
4. {  
5.    Int a = 10;  
6.    Int b = 20;   
7.    Printf("Before swapping the values in main a = %d, b = %d\n",a,b); // printing the value of a and b in main  
8.    Swap(&a,&b);  
9.    Printf("After swapping values in main a = %d, b = %d\n",a,b); // The values of actual parameters do change in call by reference, a = 10, b = 20  
10. }  
11. Void swap (int *a, int *b)  
12. {  
13.    Int temp;   
14.    Temp = *a;  
15.    *a=*b;  
16.    *b=temp;  
17.    Printf("After swapping values in function a = %d, b = %d\n",*a,*b); // Formal parameters, a = 20, b = 10   
18. }  

Output

Before swapping the values in main a = 10, b = 20

After swapping values in function a = 20, b = 10

After swapping values in main a = 20, b = 10 

Difference between call by value and call by reference in c

3.3 Passing arrays to functions

In C, there are various general problems which requires passing more than one variable of the same type to a function. For example, consider a function which sorts the 10 elements in ascending order. Such a function requires 10 numbers to be passed as the actual parameters from the main function. Here, instead of declaring 10 different numbers and then passing into the function, we can declare and initialize an array and pass that into the function. This will resolve all the complexity since the function will now work for any number of values.

As we know that the array_name contains the address of the first element. Here, we must notice that we need to pass only the name of the array in the function which is intended to accept an array. The array defined as the formal parameter will automatically refer to the array specified by the array name defined as an actual parameter.

Consider the following syntax to pass an array to the function.

1. Functionname(arrayname);//passing array  

Methods to declare a function that receives an array as an argument

There are 3 ways to declare the function which is intended to receive an array as an argument.

First way:

1. Return_type function(type arrayname[])  

Declaring blank subscript notation [] is the widely used technique.

Second way:

1. Return_type function(type arrayname[SIZE])  

Optionally, we can define size in subscript notation [].

Third way:

1. Return_type function(type *arrayname)  

You can also use the concept of a pointer. In pointer chapter, we will learn about it.

C language passing an array to function example

1. #include<stdio.h>  
2. Int minarray(int arr[],int size){    
3. Int min=arr[0];    
4. Int i=0;    
5. For(i=1;i<size;i++){    
6. If(min>arr[i]){    
7. Min=arr[i];    
8. }    
9. }//end of for    
10. Return min;    
11. }//end of function    
12.    
13. Int main(){      
14. Int i=0,min=0;    
15. Int numbers[]={4,5,7,3,8,9};//declaration of array    
16.  
17. Min=minarray(numbers,6);//passing array with size    
18. Printf("minimum number is %d \n",min);    
19. Return 0;  
20. }    

Output

Minimum number is 3

C function to sort the array

1. #include<stdio.h>   
2. Void Bubble_Sort(int[]);  
3. Void main ()    
4. {    
5.    Int arr[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};     
6.    Bubble_Sort(arr);    
7. }    
8. Void Bubble_Sort(int a[]) //array a[] points to arr.   
9. {  
10. Int i, j,temp;     
11.    For(i = 0; i<10; i++)    
12.    {    
13.        For(j = i+1; j<10; j++)    
14.        {    
15.            If(a[j] < a[i])    
16.            {    
17.                Temp = a[i];    
18.                a[i] = a[j];    
19.                a[j] = temp;     
20.            }     
21.        }     
22.    }     
23.    Printf("Printing Sorted Element List ...\n");    
24.    For(i = 0; i<10; i++)    
25.    {    
26.        Printf("%d\n",a[i]);    
27.    }  
28. }  

Output

Printing Sorted Element List ...

7 

9 

10 

12 

23

23 

34 

44 

78 

101 

Returning array from the function

As we know that, a function cannot return more than one value. However, if we try to write the return statement as return a, b, c; to return three values (a,b,c), the function will return the last mentioned value which is c in our case. In some problems, we may need to return multiple values from a function. In such cases, an array is returned from the function.

Returning an array is similar to passing the array into the function. The name of the array is returned from the function. To make a function returning an array, the following syntax is used.

1. Int * Function_name() {  
2. //some statements;   
3. Return array_type;  
4. }  

To store the array returned from the function, we can define a pointer which points to that array. We can traverse the array by increasing that pointer since pointer initially points to the base address of the array. Consider the following example that contains a function returning the sorted array.

1. #include<stdio.h>   
2. Int* Bubble_Sort(int[]);  
3. Void main ()    
4. {    
5.    Int arr[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};     
6.    Int *p = Bubble_Sort(arr), i;  
7.    Printf("printing sorted elements ...\n");  
8.    For(i=0;i<10;i++)  
9.    {  
10.        Printf("%d\n",*(p+i));  
11.    }  
12. }    
13. Int* Bubble_Sort(int a[]) //array a[] points to arr.   
14. {  
15. Int i, j,temp;     
16.    For(i = 0; i<10; i++)    
17.    {    
18.        For(j = i+1; j<10; j++)    
19.        {    
20.            If(a[j] < a[i])    
21.            {    
22.                Temp = a[i];    
23.                a[i] = a[j];    
24.                a[j] = temp;     
25.            }     
26.        }     
27.    }     
28.    Return a;  
29. }  

Output

Printing Sorted Element List ...

7 

9  

10 

12 

23

23 

34 

44 

78 

101 

3.4   Recursion: Example programs, such as Finding Factorial, Fibonacci series, Ackerman function etc

Recursion is the process which comes into existence when a function calls a copy of itself to work on a smaller problem. Any function which calls itself is called recursive function, and such function calls are called recursive calls. Recursion involves several numbers of recursive calls. However, it is important to impose a termination condition of recursion. Recursion code is shorter than iterative code however it is difficult to understand.

Recursion cannot be applied to all the problem, but it is more useful for the tasks that can be defined in terms of similar subtasks. For Example, recursion may be applied to sorting, searching, and traversal problems.

Generally, iterative solutions are more efficient than recursion since function call is always overhead. Any problem that can be solved recursively, can also be solved iteratively. However, some problems are best suited to be solved by the recursion, for example, tower of Hanoi, Fibonacci series, factorial finding, etc.

In the following example, recursion is used to calculate the factorial of a number.

1. #include <stdio.h>  
2. Int fact (int);  
3. Int main()  
4. {  
5.    Int n,f;  
6.    Printf("Enter the number whose factorial you want to calculate?");  
7.    Scanf("%d",&n);  
8.    f = fact(n);  
9.    Printf("factorial = %d",f);  
10. }  
11. Int fact(int n)  
12. {  
13.    If (n==0)  
14.    {  
15.        Return 0;  
16.    }  
17.    Else if ( n == 1)  
18.    {  
19.        Return 1;  
20.    }  
21.    Else   
22.    {  
23.        Return n*fact(n-1);  
24.    }  
25. }  

Output

Enter the number whose factorial you want to calculate?5

Factorial = 120

We can understand the above program of the recursive method call by the figure given below:

Recursive Function

A recursive function performs the tasks by dividing it into the subtasks. There is a termination condition defined in the function which is satisfied by some specific subtask. After this, the recursion stops and the final result is returned from the function.

The case at which the function doesn't recur is called the base case whereas the instances where the function keeps calling itself to perform a subtask, is called the recursive case. All the recursive functions can be written using this format.

Pseudocode for writing any recursive function is given below.

1. If (test_for_base)  
2. {  
3.    Return some_value;  
4. }  
5. Else if (test_for_another_base)  
6. {  
7.    Return some_another_value;  
8. }  
9. Else  
10. {  
11.    // Statements;  
12.    Recursive call;  
13. }  

Example of recursion in C

Let's see an example to find the nth term of the Fibonacci series.

1. #include<stdio.h>  
2. Int fibonacci(int);  
3. Void main ()  
4. {  
5.    Int n,f;  
6.    Printf("Enter the value of n?");  
7.    Scanf("%d",&n);  
8.    f = fibonacci(n);  
9.    Printf("%d",f);  
10. }  
11. Int fibonacci (int n)  
12. {  
13.    If (n==0)  
14.    {  
15.    Return 0;  
16.    }  
17.    Else if (n == 1)  
18.    {  
19.        Return 1;   
20.    }  
21.    Else  
22.    {  
23.        Return fibonacci(n-1)+fibonacci(n-2);  
24.    }  
25. }  

Output

Enter the value of n?12

144

Memory allocation of Recursive method

Each recursive call creates a new copy of that method in the memory. Once some data is returned by the method, the copy is removed from the memory. Since all the variables and other stuff declared inside function get stored in the stack, therefore a separate stack is maintained at each recursive call. Once the value is returned from the corresponding function, the stack gets destroyed. Recursion involves so much complexity in resolving and tracking the values at each recursive call. Therefore, we need to maintain the stack and track the values of the variables defined in the stack.

Let us consider the following example to understand the memory allocation of the recursive functions.

1. Int display (int n)  
2. {  
3.    If(n == 0)  
4.        Return 0; // terminating condition  
5.    Else   
6.    {  
7.        Printf("%d",n);  
8.        Return display(n-1); // recursive call  
9.    }  
10. }  

Explanation

Let us examine this recursive function for n = 4. First, all the stacks are maintained which prints the corresponding value of n until n becomes 0, Once the termination condition is reached, the stacks get destroyed one by one by returning 0 to its calling stack. Consider the following image for more information regarding the stack trace for the recursive functions.

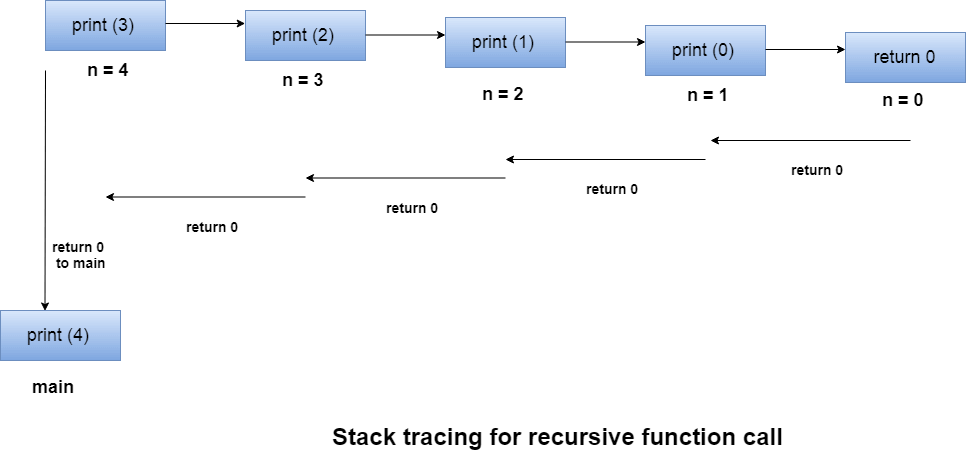
A function that calls itself is known as a recursive function. And, this technique is known as recursion.

How recursion works?

Void recurse()

{

... .. ...

Recurse();

... .. ...

}

Int main()

{

... .. ...

Recurse();

... .. ...

}

The recursion continues until some condition is met to prevent it.

To prevent infinite recursion, if...else statement (or similar approach) can be used where one branch makes the recursive call, and other doesn't.

Example: Sum of Natural Numbers Using Recursion

#include <stdio.h>

Int sum(int n);

Int main() {

Int number, result;

Printf("Enter a positive integer: ");

Scanf("%d", &number);

Result = sum(number);

Printf("sum = %d", result);

Return 0;

}

Int sum(int n) {

If (n != 0)

// sum() function calls itself

Return n + sum(n-1);

Else

Return n;

}

Output

Enter a positive integer:3

Sum = 6

Initially, the sum() is called from the main() function with number passed as an argument.

Suppose, the value of n inside sum() is 3 initially. During the next function call, 2 is passed to the sum() function. This process continues until n is equal to 0.

When n is equal to 0, the if condition fails and the else part is executed returning the sum of integers ultimately to the main() function.

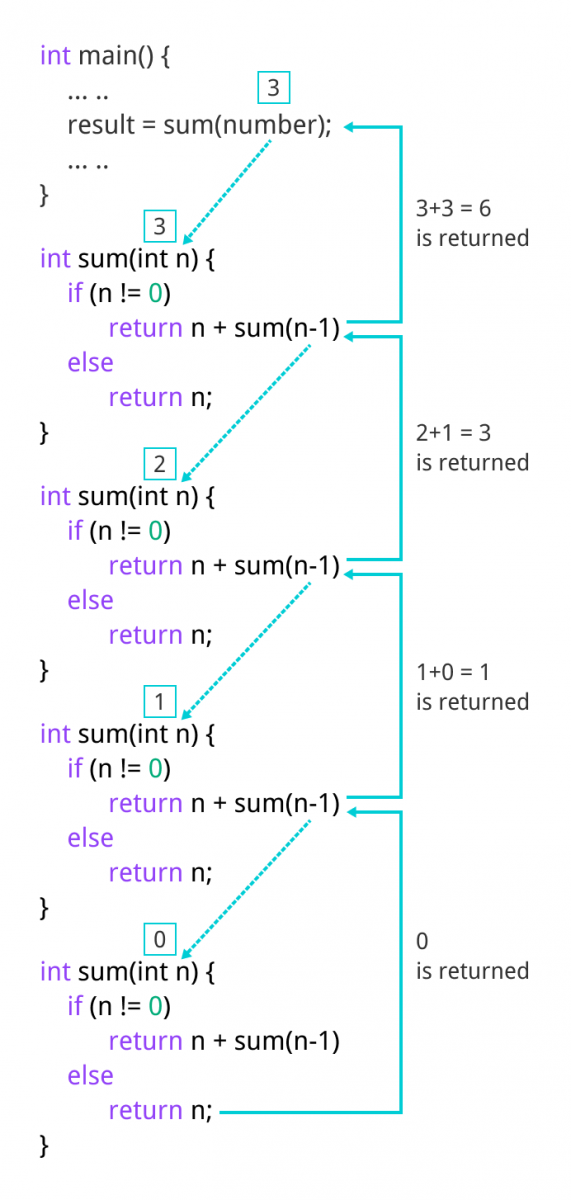
Advantages and Disadvantages of Recursion

Recursion makes program elegant. However, if performance is vital, use loops instead as recursion is usually much slower.

That being said, recursion is an important concept. It is frequently used in data structure and algorithms. For example, it is common to use recursion in problems such as tree traversal.

Program to find factorial of number using Recursion

This Program prompts user for entering any integer number, finds the factorial of input number and displays the output on screen. We will use a recursive user defined function to perform the task. Here we have a function find_factorial that calls itself in a recursive manner to find out the factorial of input number. We have involved the user interaction in the below program, however if you do not want that part then you can simply assign an integer value to variable num and ignore the scanf statement. In short you can tweak it in any way you want, the logic would be the same for each case.

Program to find factorial

/* Program Name: Find Factorial

Written by: Chaitanya Singh

Published on: beginnersbook.com

*/

#include<stdio.h>

Int find_factorial(int);

Int main()

{

Int num, fact;

//Ask user for the input and store it in num

Printf("\nEnter any integer number:");

Scanf("%d",&num);

//Calling our user defined function

Fact =find_factorial(num);

//Displaying factorial of input number

Printf("\nfactorial of %d is: %d",num, fact);

Return 0;

}

Int find_factorial(int n)

{

//Factorial of 0 is 1

If(n==0)

Return(1);

//Function calling itself: recursion

Return(n*find_factorial(n-1));

}

Output:

Enter any integer number: 4

Factorial of 4 is: 24

Fibonacci Series

Fibonacci Series in C: In case of fibonacci series, next number is the sum of previous two numbers for example 0, 1, 1, 2, 3, 5, 8, 13, 21 etc. The first two numbers of fibonacci series are 0 and 1.

There are two ways to write the fibonacci series program:

• Fibonacci Series without recursion
• Fibonacci Series using recursion

Fibonacci Series in C without recursion

Let's see the fibonacci series program in c without recursion.

1. #include<stdio.h>    
2. Int main()    
3. {    
4. Int n1=0,n2=1,n3,i,number;    
5. Printf("Enter the number of elements:");    
6. Scanf("%d",&number);    
7. Printf("\n%d %d",n1,n2);//printing 0 and 1    
8. For(i=2;i<number;++i)//loop starts from 2 because 0 and 1 are already printed    
9. {    
10.  n3=n1+n2;    
11.  Printf(" %d",n3);    
12.  n1=n2;    
13.  n2=n3;    
14. }  
15.  Return 0;  
16. }    

Output:

Enter the number of elements:15

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377

Fibonacci Series using recursion in C

Let's see the fibonacci series program in c using recursion.

1. #include<stdio.h>    
2. Void printFibonacci(int n){    
3.    Static int n1=0,n2=1,n3;    
4.    If(n>0){    
5.         n3 = n1 + n2;    
6.         n1 = n2;    
7.         n2 = n3;    
8.         Printf("%d ",n3);    
9.         PrintFibonacci(n-1);    
10.    }    
11. }    
12. Int main(){    
13.    Int n;    
14.    Printf("Enter the number of elements: ");    
15.    Scanf("%d",&n);    
16.    Printf("Fibonacci Series: ");    
17.    Printf("%d %d ",0,1);    
18.    PrintFibonacci(n-2);//n-2 because 2 numbers are already printed    
19.  Return 0;  
20. }    

Output:

Enter the number of elements:15

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377

Ackermann Function

In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive. All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive. It’s a function with two arguments each of which can be assigned any non-negative integer.

Ackermann function is defined as:

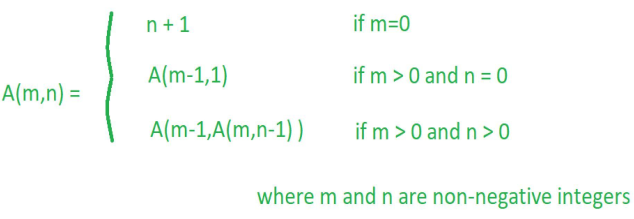
Ackermann algorithm:

Ackermann(m, n)

{next and goal are arrays indexed from 0 to m, initialized so that next[O]

Through next[m] are 0, goal[O] through goal[m - l] are 1, and goal[m] is -1}

Repeat

Value <-- next[O] + 1

Transferring <-- true

Current <-- O

While transferring do begin

If next[current] = goal[current] then goal[current] <-- value

Else transferring <-- false

Next[current] <-- next[current]+l

Current <-- current + 1

End while

Until next[m] = n + 1

Return value {the value of A(m, n)}

End Ackermann

Here’s the explanation of the given Algorithm:
Let me explain the algorithm by taking the example A(1, 2) where m = 1 and n = 2
So according to the algorithm initially the value of next, goal, value and current are:

Though next[current] != goal[current], so else statement will execute and transferring become false.
So now, the value of next, goal, value and current are:

Similarly by tracing the algorithm until next[m] = 3 the value of next, goal, value and current are changing accordingly. Here’s the explanation how the values are changing,

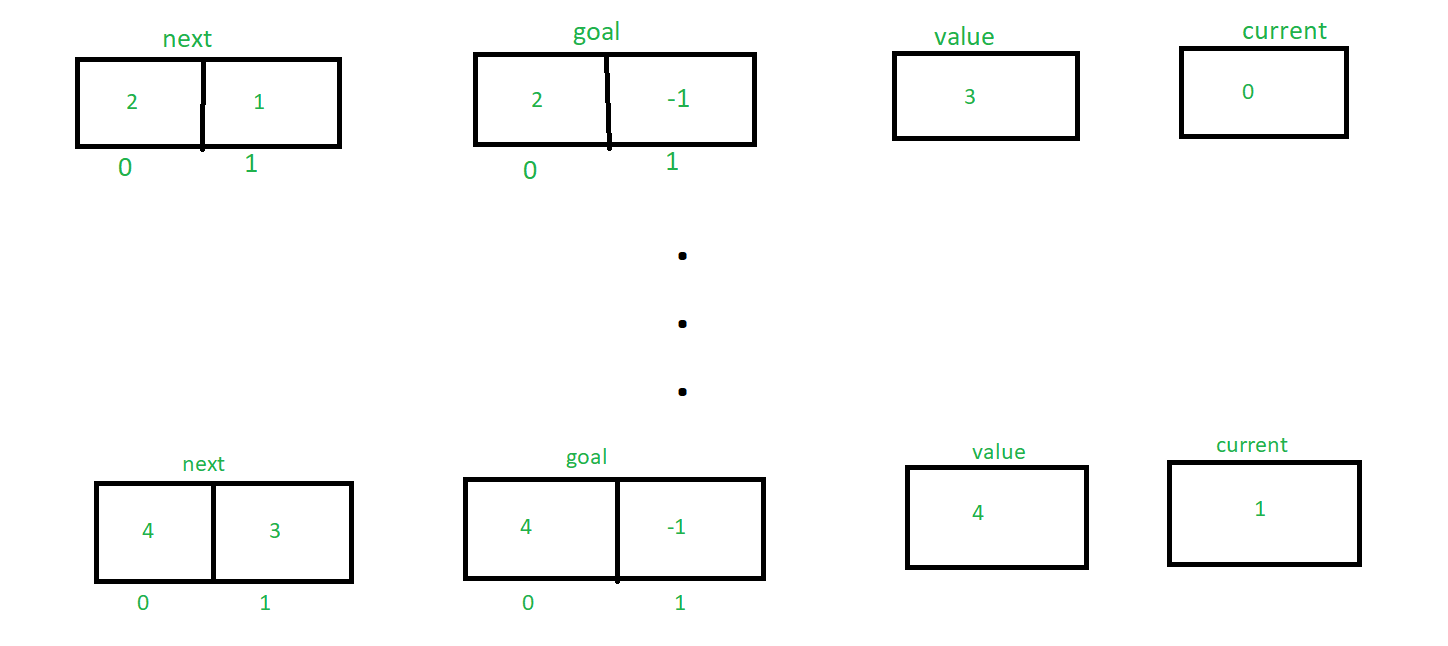
Finally returning the value e.g 4

Analysis of this algorithm:

• The time complexity of this algorithm is: O(mA(m, n)) to compute A(m, n)
• The space complexity of this algorithm is: O(m) to compute A(m, n)

Let’s understand the definition by solving a problem!

Solve A(1, 2)?

Answer:

Given problem is A(1, 2)
Here m = 1, n = 2 e.g m > 0 and n > 0
Hence applying third condition of Ackermann function
A(1, 2) = A(0, A(1, 1)) ———- (1)
Now, Let’s find A(1, 1) by applying third condition of Ackermann function
A(1, 1) = A(0, A(1, 0)) ———- (2)
Now, Let’s find A(1, 0) by applying second condition of Ackermann function
A(1, 0) = A(0, 1) ———- (3)
Now, Let’s find A(0, 1) by applying first condition of Ackermann function
A(0, 1) = 1 + 1 = 2
Now put this value in equation 3
Hence A(1, 0) = 2
Now put this value in equation 2
A(1, 1) = A(0, 2) ———- (4)
Now, Let’s find A(0, 2) by applying first condition of Ackermann function
A(0, 2) = 2 + 1 = 3
Now put this value in equation 4
Hence A(1, 1) = 3
Now put this value in equation 1
A(1, 2) = A(0, 3) ———- (5)
Now, Let’s find A(0, 3) by applying first condition of Ackermann function
A(0, 3) = 3 + 1 = 4
Now put this value in equation 5
Hence A(1, 2) = 4

So, A (1, 2) = 4

Let’s solve another two questions on this by yourself!

Question: Solve A(2, 1)?
Answer: 5

Question: Solve A(2, 2)?
Answer: 7

Here is the simplest c and python recursion function code for generating Ackermann function

3.6   Quick sort or Merge sort

Quick Sort

Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value.

Implementation in C

#include <stdio.h>

#include <stdbool.h>

#define MAX 7

Int intArray[MAX] = {4,6,3,2,1,9,7};

Void printline(int count) {

Int i;

For(i = 0;i < count-1;i++) {

Printf("=");

}

Printf("=\n");

}

Void display() {

Int i;

Printf("[");

// navigate through all items

For(i = 0;i < MAX;i++) {

Printf("%d ",intArray[i]);

}

Printf("]\n");

}

Void swap(int num1, int num2) {

Int temp = intArray[num1];

IntArray[num1] = intArray[num2];

IntArray[num2] = temp;

}

Int partition(int left, int right, int pivot) {

Int leftPointer = left -1;

Int rightPointer = right;

While(true) {

While(intArray[++leftPointer] < pivot) {

//do nothing

}

While(rightPointer > 0 && intArray[--rightPointer] > pivot) {

//do nothing

}

If(leftPointer >= rightPointer) {

Break;

} else {

Printf(" item swapped :%d,%d\n", intArray[leftPointer],intArray[rightPointer]);

Swap(leftPointer,rightPointer);

}

}

Printf(" pivot swapped :%d,%d\n", intArray[leftPointer],intArray[right]);

Swap(leftPointer,right);

Printf("Updated Array: ");

Display();

Return leftPointer;

}

Void quickSort(int left, int right) {

If(right-left <= 0) {

Return;  

} else {

Int pivot = intArray[right];

Int partitionPoint = partition(left, right, pivot);

QuickSort(left,partitionPoint-1);

QuickSort(partitionPoint+1,right);

}       

}

Int main() {

Printf("Input Array: ");

Display();

Printline(50);

QuickSort(0,MAX-1);

Printf("Output Array: ");

Display();

Printline(50);

}

If we compile and run the above program, it will produce the following result −

Output

Input Array: [4 6 3 2 1 9 7 ]

==================================================

Pivot swapped :9,7

Updated Array: [4 6 3 2 1 7 9 ]

Pivot swapped :4,1

Updated Array: [1 6 3 2 4 7 9 ]

Item swapped :6,2

Pivot swapped :6,4

Updated Array: [1 2 3 4 6 7 9 ]

Pivot swapped :3,3

Updated Array: [1 2 3 4 6 7 9 ]

Output Array: [1 2 3 4 6 7 9 ]

==================================================

Merge Sort

Merge sort is a sorting technique based on divide and conquer technique. With the worst-case time complexity being Ο(n log n), it is one of the most respected algorithms.

Implementation in C

We shall see the implementation of merge sort in C programming language here −

#include <stdio.h>

#define max 10

Int a[11] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };

Int b[10];

Void merging(int low, int mid, int high) {

Int l1, l2, i;

For(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {

If(a[l1] <= a[l2])

b[i] = a[l1++];

Else

b[i] = a[l2++];

}

While(l1 <= mid)   

b[i++] = a[l1++];

While(l2 <= high)  

b[i++] = a[l2++];

For(i = low; i <= high; i++)

a[i] = b[i];

}

Void sort(int low, int high) {

Int mid;

If(low < high) {

Mid = (low + high) / 2;

Sort(low, mid);

Sort(mid+1, high);

Merging(low, mid, high);

} else {

Return;

}  

}

Int main() {

Int i;

Printf("List before sorting\n");

For(i = 0; i <= max; i++)

Printf("%d ", a[i]);

Sort(0, max);

Printf("\nList after sorting\n");

For(i = 0; i <= max; i++)

Printf("%d ", a[i]);

}

If we compile and run the above program, it will produce the following result −

Output

List before sorting

10 14 19 26 27 31 33 35 42 44 0

List after sorting

0 10 14 19 26 27 31 33 35 42 44

Text Books

(i) Byron Gottfried, Schaum's Outline of Programming with C, McGraw-Hill

(ii) E. Balaguruswamy, Programming in ANSI C, Tata McGraw-Hill

Reference Books

(i) Brian W. Kernighan and Dennis M. Ritchie, The C Programming Language, Prentice Hall of India.