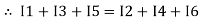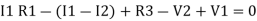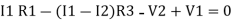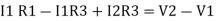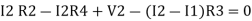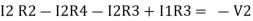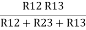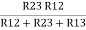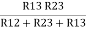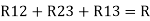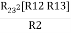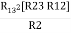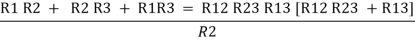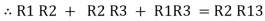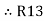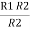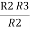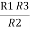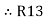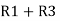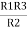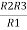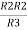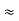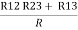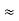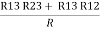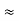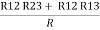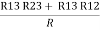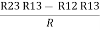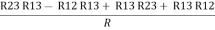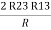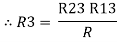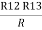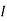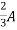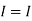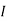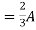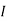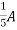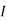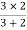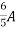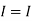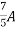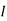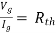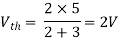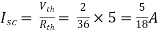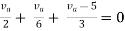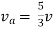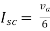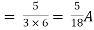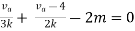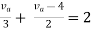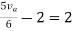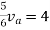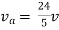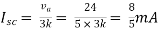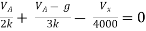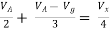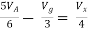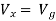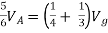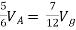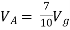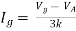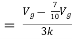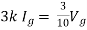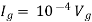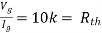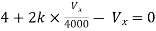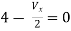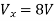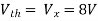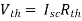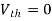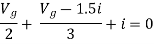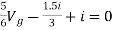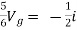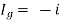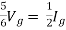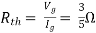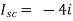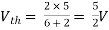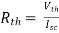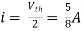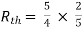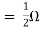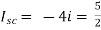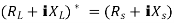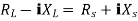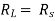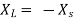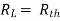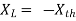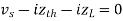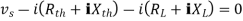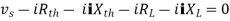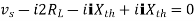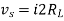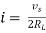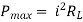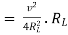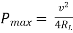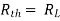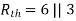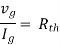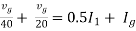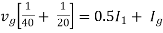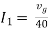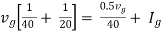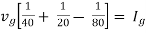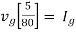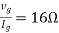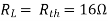1.1 Electrical Circuit Elements R L And C | unit 1 dc circuits

Back to Study material

BEE

Unit – 1

DC Circuits

1.1 Electrical Circuit Elements (R, L And C)

# In case of capacitor: -

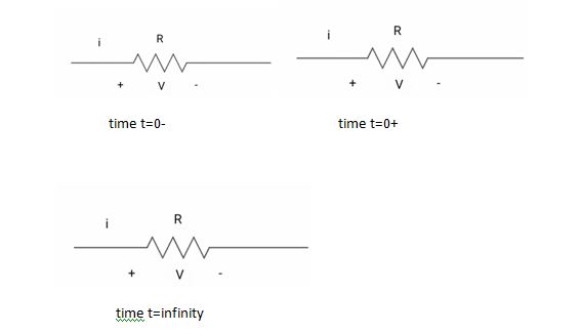
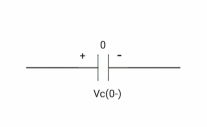
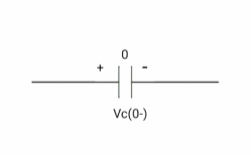
At time t= 0-

:. Capacitor is initially uncharged

Q (0-) =0

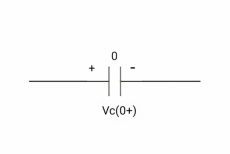
Q=cv

Q (0-) = cvc (0-)

Vc (0-) =0

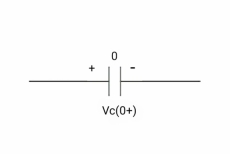
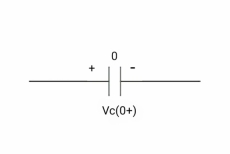
At time t= 0+

By low of conservation of charges

Q (0-) = Q (0+)

Cvc (0-) =cvc (0+)

Vc (0+) =0

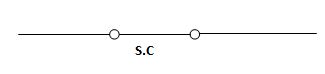
Hence acts as

If capacitor is initially uncharged at t= 0- than voltage across capacitor is zero at t=0+ capacitor will follow low of consvation of charges and Vc (0+) =0 it means at t=0+ capacitor behaves as short circuit in other words, voltage across capacitor cannot change instantaneously.

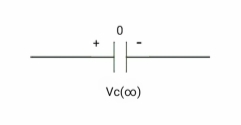
At time t= infinity,

I = cdvc/dt constant and maximum

hence, i= 0

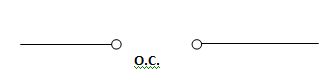
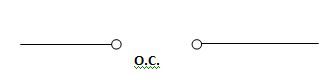
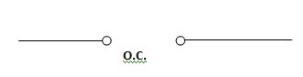
At t= infinity capacitor will be fully charged or voltage across capacitor is constant and current through capacitor is zero so, capacitor will behave as open –circuit

Say capacitor is initially charged

at time t= 0-,

at time t= 0+,

at time t= 0+

Q (0-) = Q (0+)

Cvc (0-) =cvc (0+)

V1 = Vc (0+)

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_170304.jpg$

Hence acts as

Its capacitor is initially charged at t= 0- as voltage across capacitor is V1 than at t=0+ capacitor behaves as a voltage as a voltage source with value V1

At time t = infinity

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_171756.jpg$

If capacitor is initially charged and it is connected to any independent source for long time than current through capacitor is 3 etw and capacitor will be fully charged and it behaves as o.c

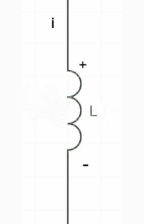
# for Inductor: -

At time t= 0-

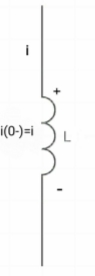
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\Screenshot_2019-12-29-17-11-12-410_com.miui.gallery.jpg$

Ø= Li =0

Ø (0) = Li (0-)

i (0-) =0

at t= 0+,

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_172121.jpg$

by low of conservation of flux

Ø (0-) = Ø (0+)

Li (0-) = Li (0+)

0 =i (0+)

Hence, acts as short circuit

1.2 Voltage And Current Sources

Ideal and practical Voltage and Current source:

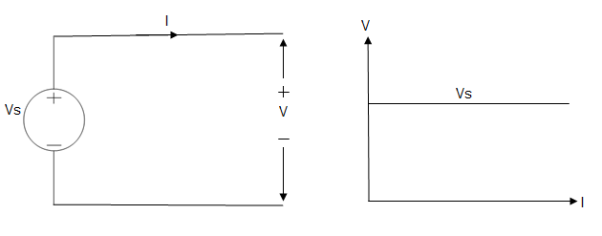
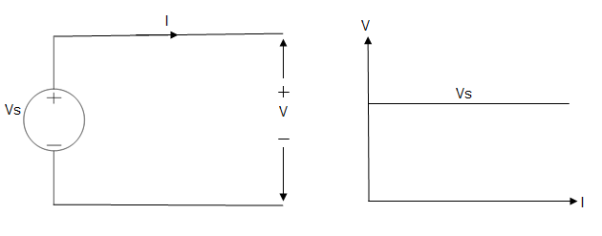
A voltage source is a device which provides a constant voltage to load at any instance of time and is independent of the current drawn from it. This type of source is known as an ideal voltage source. Practically, the ideal voltage source cannot be made. It has zero internal resistance. It is denoted by this symbol.

img 1.png

Fig: Voltage source symbol

Ideal Voltage Source

img 2.png

Fig: Ideal Voltage Source

The graph represents the change in voltage of the voltage source with respect to time. It is constant at any instance of time.

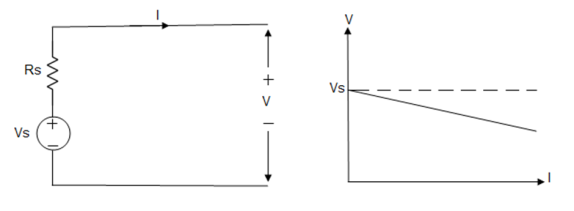
Voltage sources that have some amount of internal resistance are known as a practical voltage source. Due to this internal resistance, voltage drop takes place. If the internal resistance is high, less voltage will be provided to load and if the internal resistance is less, the voltage source will be closer to an ideal voltage source. A practical voltage source is thus denoted by a resistance in series which represents the internal resistance of source.

Practical Voltage source

img 2.png

Fig: Practical Voltage source

The graph represents the voltage of the voltage source with respect to time. It is not constant but it keeps on decreasing as the time passes.

Current source

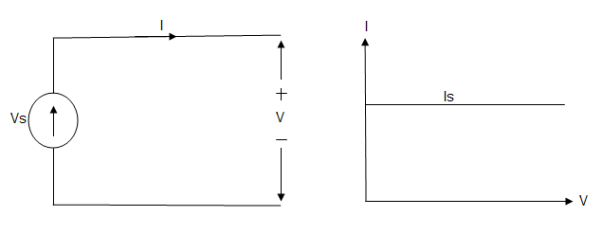
A current source is a device which provides the constant current to load at any time and is independent of the voltage supplied to the circuit. This type of current is known as an ideal current source; practically ideal current source is also not available. It has infinite resistance. It is denoted by this symbol.

Ideal Current source

img 3.png

Fig: Ideal Current source

The graph represents the change in current of the current source with respect to time. It is constant at any instance of time.

Why ideal Current source has infinite resistance?

A current source is used to power a load, so that load will turn on. We try to supply 100% of the power to load. For that, we connect some resistance to transfer 100% of power to load because the current always takes the path of least resistance. So, in order for current to go to the path of least resistance, we must connect resistance higher than load. This is why we have the ideal current source to have infinite internal resistance. This infinite resistance will not affect voltage sources in the circuit.

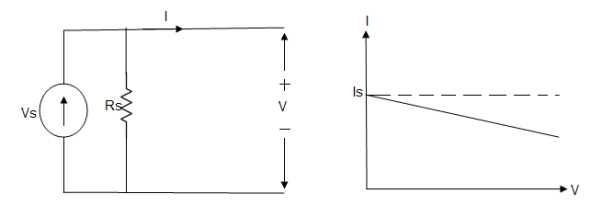
Practical Current source

Practically current sources do not have infinite resistance across there but they have a finite internal resistance. So the current delivered by the practical current source is not constant and it is also dependent somewhat on the voltage across it.

A practical current source is represented as an ideal current source connected with resistance in parallel.

img 4.png

Fig; Practical Current source

The graph represents the current of the current source with respect to time. It is not constant but it also keeps on decreasing as the time passes.

Examples of current and voltage sources

The examples of current source are solar cells, transistors and examples of some voltage sources are batteries and alternators.

This was all about ideal and practical sources of power. The ideal sources are very useful for calculations in theory but as ideal sources are not practically possible, only practical sources are used in practical circuits. The batteries we use are a practical source of power and the voltage and current decreases as we use it. Thus both are useful to us in their own ways.

1.3 Kirchhoff Current And Voltage Laws

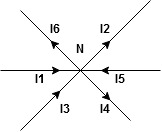
The algebraic sum of currents meeting at a junction or node in a electric circuit is zero or the summation of all incoming current is always equal to summation of all outgoing current in an electrical network.

Explanation

$C:\Users\ManishM\Downloads\BEE5_2$

Assuming the incoming current to be positive and outgoing current negative we have

I e incoming current = ∑ outgoing current thus, the above Law can also be stated as the sum of current flowing towards any junction in an electric circuit is equal to the sum of currents flowing away from that junction

Kirchhoff’s Voltage Law (KVL)

statement : the algebraic summation of all Voltage in any closed circuit or mesh of loop zero.

ie ∑ Voltage in closed loop = 0 the summation of the Voltage rise (voltage sources) is equal to summation of the voltage drops around a closed loop in 0 circuit for explanation from here

determination of sigh and direction of currents (Don’t write in exams just for understanding)

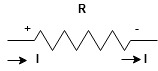
$C:\Users\ManishM\Downloads\BEE5_3$

current entering a resistor is +ve and leaving should be –ve

now

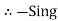
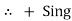
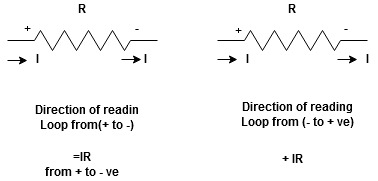
$C:\Users\ManishM\Downloads\BEE5_4$

Potential Rise Potential Drop

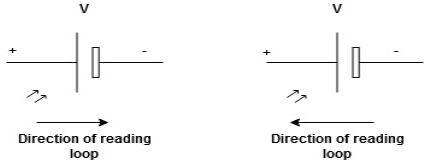
$C:\Users\ManishM\Downloads\BEE5_5$

We are reading from +V to –V we are reading from –V to +V

potential drops potential rise

-V +V

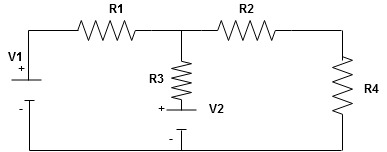
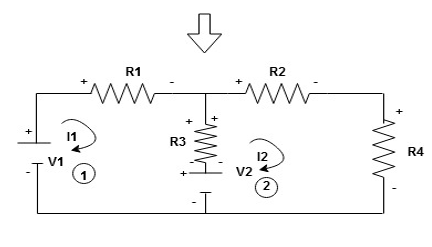
Given Circuit

$C:\Users\ManishM\Downloads\BEE5_6$

First identify no of loops and assign direction of current flowing in loop

Note : no of loops in circuit = No, of unknown currents = no, of equations in the circuit

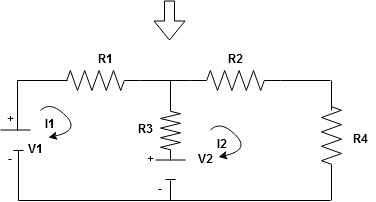
$C:\Users\ManishM\Downloads\BEE5_7$

Note : keep loop direction and current direction same ie either clockwise or anticlockwise for all loops I1 I2

Now according to direction of direction assign signs (+ve to –ve) to the resistors

$C:\Users\ManishM\Downloads\BEE5_8$

Note : voltage sources (V) polarities does not change is constant.

Note: for common resistor between 2 loops appearing in the circuit like R3 give signs according to separate loops as shown

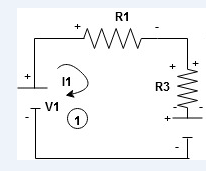
$C:\Users\ManishM\Desktop\R1.PNG$

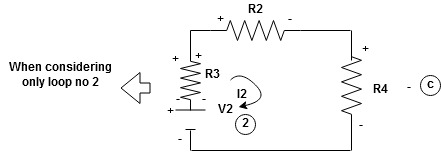
 When considering only loop no 1 (+ R3 - )

- B

$C:\Users\ManishM\Downloads\bee5_11$

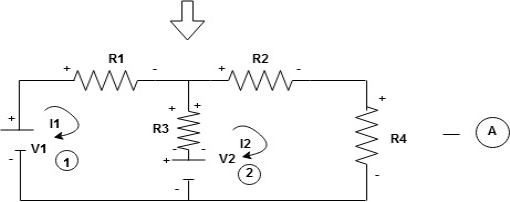
Now consider diagram A and write equations

Two loops two unknown currents two equation

Apply KVL for loop ① [B. Diagram ]

(+ to drop -) = - sign and (- to rise +) = + sign

for drop = -sign

for rise = + sign

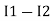-() R2 is considered because in R3,2 currents are flowing 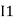and 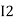and we have taken (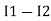) because we are considering loop no 1 and current flowing is 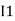in loop no 1

)

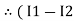Similarly for loop no. 2 currents flowing is 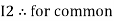resistor R3 it should be 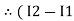)R3

$C:\Users\ManishM\Desktop\r3.PNG$

Consider loop no. 1 apply KVL

- …….①

Consider loop no. 2 apply KVL

-…….②

After solving equation ① and ② we will get branch current 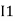and

1.4 Analysis Of Simple Circuits With Dc Excitation

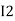
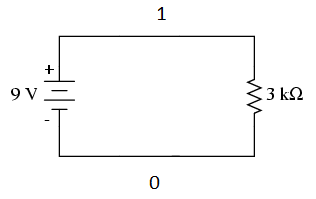
Here is a simple circuit with DC excitation:

Analysis would mean we determine the voltages at all the nodes and currents in all the branches of this circuit.

A node is defined as any point where two or more components meet.

A branch is defined as any path between two nodes.

Let’s label all the nodes in the circuit above:

We have only two nodes here, ‘1’ and ‘0’.

We call node ‘0’ the ground node. The ground node is at 0 volt.

Node ‘1’ is connected to the top of our DC voltage source. So it is at 9 volts.

Half our job is done here, because we now know the voltages at all the nodes in our circuit.

Next, let’s talk about the branches.

There are two branches in our circuit. One branch contains the 9V DC source and the other branch contains the 3k resistor.

We know find the currents through the branches.

From Ohm’s law we can calculate the current in the resistor.

I = V/R

This gives us a current of 9/3k = 3 mA.

The current in the resistor branch is 3 mA. And, because our circuit is one single closed loop, this current also flows in the other branch.

At this point, we know all the voltages at each node and the currents through each branch of our simple circuit. So, we say that the analysis of our simple DC excitation circuit is complete.

1.5 Star-Delta Conversion

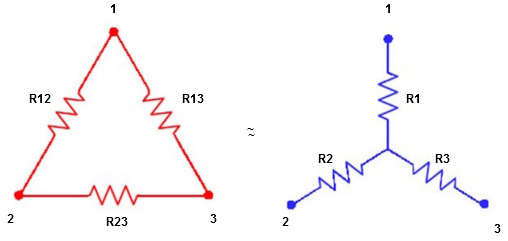
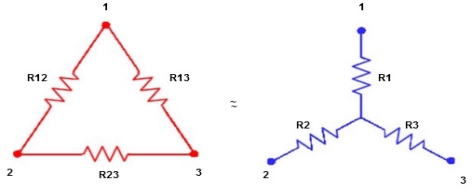
Star to delta conversion to final equivalent resistance

$C:\Users\ManishM\Downloads\BEE5_1$

We know that (from delta to star conversion)

R1 = …….①

R2 = …..②

R1 = ……③

Multiply ① X ② L.H.S and R.H.S

R1 R2 = …….④ where

Similarly multiply ② X ③

R2 R3 = …….⑤

And ③ X①

R1 R3 = …….⑥

Now add equation ④, ⑤, and ⑥ L.H.S and R.H.S

……refer eq. ②

= + +

= +

(Delta) star star

Similarly R23 = R2+R3 +

R23 = R1+R2 +

Delta to Star Conversion to Find (Req.)

$C:\Users\ManishM\Downloads\BEE5_1$

Equivalent resistance between ① and ②

Delta Star

= R12// (R23 + R13) =R1 + R2

= = R1 + R2

Here let R = R12 + R23 + R13

Similarly we can find Req. between 2 and 3

= R2 + R3

Similarly we can find req. between 1 and 3

R1 + R3

Now the 3 equations after equating L.H.S. and R.H.S

R1 + R2 = …….①

R2 + R3 = ……②

R1 + R3 = …..③

Now subtract ② and ① on L.H.S. and R.H.S

R2+ R3 – R1 – R2 =

R3 – R1 = …..④

Now add equation ④ and ③

R3 – R1 + R1 + R3 =

2R3 =

Similarly R1 =

And R2 = R23 R12/R where R = R12 + R23 + R13

ie star equivalent from delta network is ratio of product of adjacent branches in delta to the addition of all branches in delta.

1.6 Network Theorems (Superposition, Thevenin, Norton And Maximum Power Transfer Theorems)

Superposition Theorem

This is only applicable to circuits with linear elements.
If two or more than two independent sources (voltage or current) are operating in the circuit than voltage across any element or current through any element is sum of current and voltages due to individual sources.

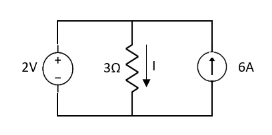
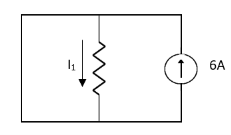
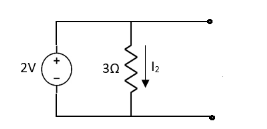
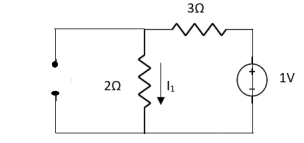
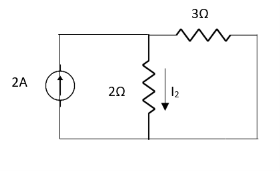
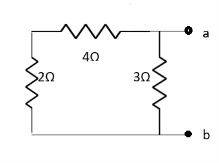
Question 1. Find the current through 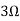resistance.

Solution:

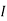1= 0

1 + 2

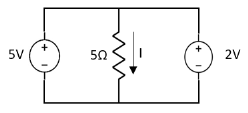
Special Case:

Since two voltage sources with different magnitude in parallel which cannot be connected as in single branch two different current is not possible (if 5V than I = zero).

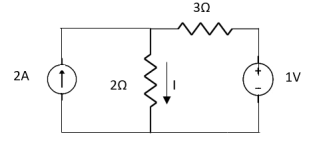
Question:

1 =

2 =

1 + 2

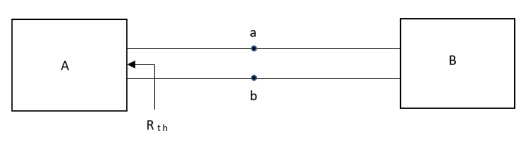
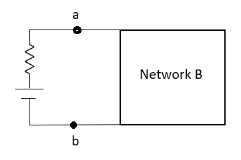
Thevenin’s and Norton’s Theorem

Thevenin’s equivalent of A

Norton’s equivalent of A

sc = Vth/Rth

Norton’s equivalent is obtained by source conversion of thevenin’s

equivalent circuit.

CONDITIONS FOR APPLICATION

For network A:

Network A should contain linear elements.
Network A can have independent and dependent current and voltage source.
If network A has dependent source than controlling parameter must lie in network A itself.
Network A should not have any source coupling and magnetic coupling.

For network B:

It can have linear and non linear elements.
It can have dependent and independent voltage and current sources.
It should not have any source and magnetic coupling with network A.

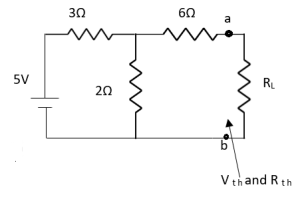
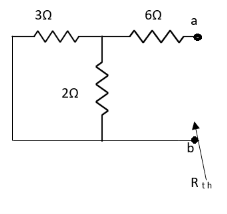
 Method for finding Rth :

Firstly, open circuit terminal A and B.

If network is operating with only independent sources:

Make all sources zero in network A.
Find out the equivalent resistance across terminal A and B.

2. If network A is operating with independent and dependent sources:

Make all independent sources zero in network A.
Connect a generation between A and B.

3. If network is operating with only dependent sources:

Connect generation between A and B

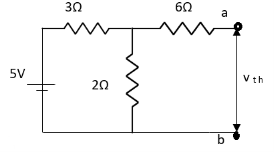
Method for Vth:

First open circuit terminal A and B.

Find out the voltage between A and B this is Vth

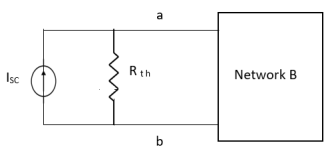
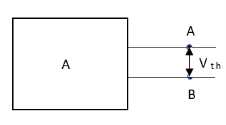
Method for Isc:

Isc =
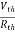
Remove network B and S.C. the terminal A and B and current from terminal A to B Isc.

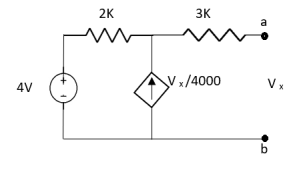
Question:

Answer:

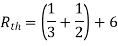
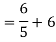
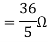
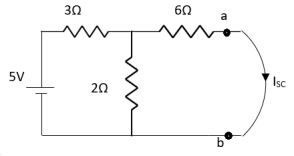
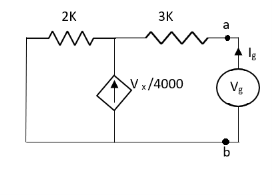
Finding Isc from circuit directly:

By KCL,

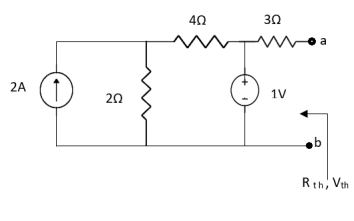
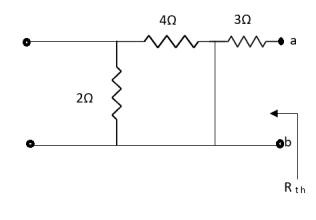
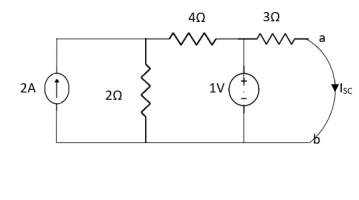
Question:

Answer

Also, clear from circuit that Vth = 1V.

By applying KVL we get,

	1-3Isc=0
Isc=A

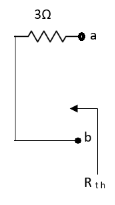
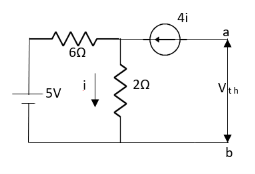
Que:

Ans;

Rth=3k+2k=5k

By applying KVL we get

Therefore,

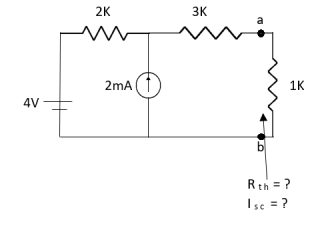
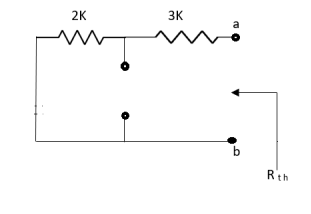
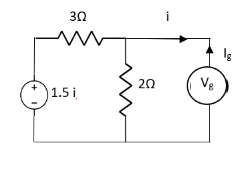
Question:

Solution: For Rth

By KCL, But,
	By KVL,

Question:

Solution: Since, no independent source is present so,

Isc = 0

And we know that,

Since Rth cannot be zero

But

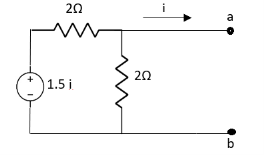
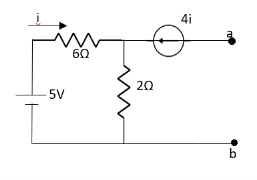
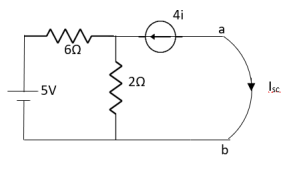
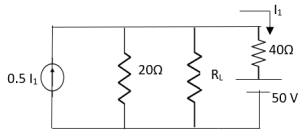
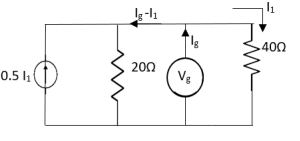
Question: Find out the Norton’s equivalent

Solution:

Since, there is no significance of current source

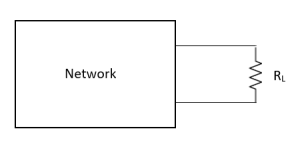
Maximum Power Transfer Theorem

where Rth is Thevenin’s equivalent resistance across a and b.

Maximum power is absorbed by ZL when

Condition: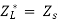

Comparing real and imaginary parts

Maximum power absorbed by ZL is

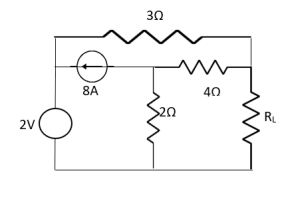
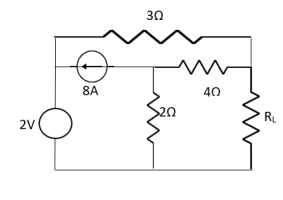
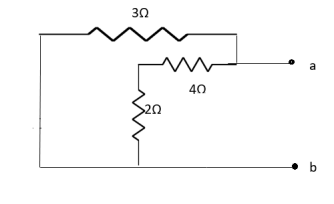
Question: Find out the value of load resistance if power absorbed is maximum.

Solution: find Thevenin’s equation

Question: Find maximum power delivered is RLif its value is

16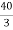Ω
Ω
60Ω
20Ω

Solution



	Therefore,

1.7 Time-Domain Analysis Of First-Order R-L And R-C Circuits

The transient response means the change in the response of output with respect to time. So, using initial conditions, and solution for differential equations we solve some numerical.

Diagram

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_181102.jpg$

If switch ‘s’ closed at t= 0 find out the voltage across capacitor and current through capacitor at t= 0+?

Soln: at t= 0- switch was open so,

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_175854.jpg$

:. There is no potential so Vc (0-) = 0

At t= 0+, Vc (0-) = Vc (0+) = 0

Diagram

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_181034.jpg$

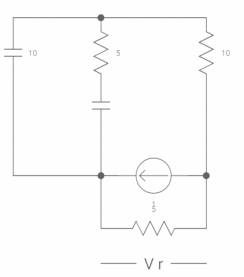
Isc = 10/5 = 2 A

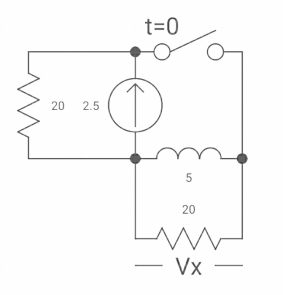
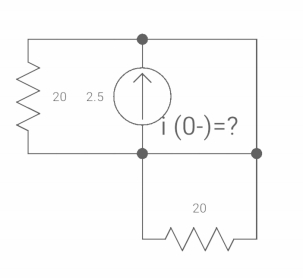
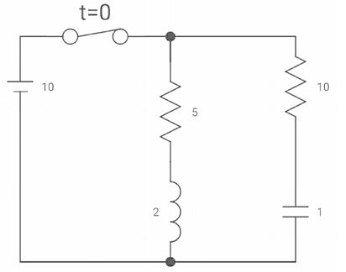
Diagram

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_182433.jpg$

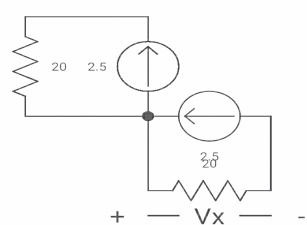
The switch was closed for long time before

Opening at t=0- find VX (0+)?

(a) 25V (b) 50 V (c)-50V (d) 0V

soln at time t=0-

$C:\Users\TARUNA\Desktop\qq\3.JPG$

clearly, il (0-) = 2.5 A

at t= 0+, as inductor is initially charges

so il (0-) = il (0+)

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_182547.jpg$

-VX= 20/2.5 20*2.5

VX= -50A

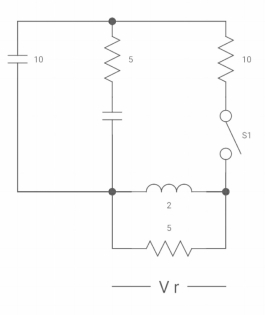
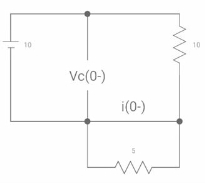
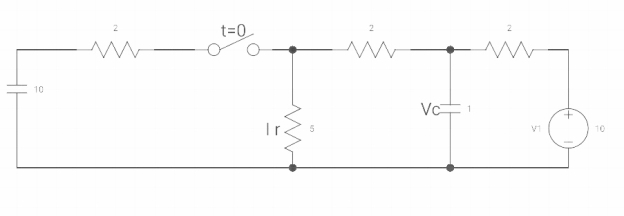
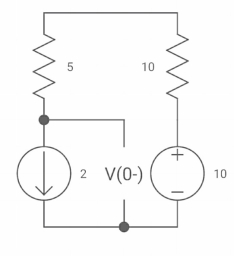
Ques:

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_183527.jpg$

VR (0+) =

dil/dt(t) = 0+?

If switch is opened at t= 0?

Soln: -

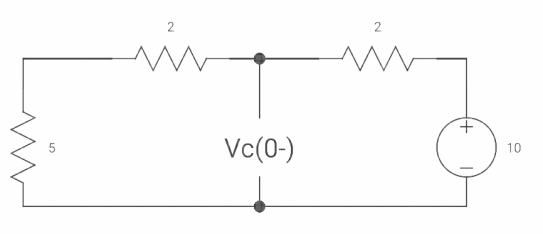
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_190915.jpg$

At t=0-

Vc (0-) = 10V

IL (0-) = 10/10 = 1 A

Also, iL (0-) = iL (0+) = 1A

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_190932.jpg$

VR(0+) = 5V Ldi(t)/dt = VL (t) DiL(t)/dt = VL(t)/L At t= 0+ d/dt iL (0+) = VL (0+)/L
	-VL (0+)-VR =0 VL (0+) = -5V dt(t) at t = ot = vl (ot)/L =-5/2
		dil/dt(o+) = 2.5 A/s

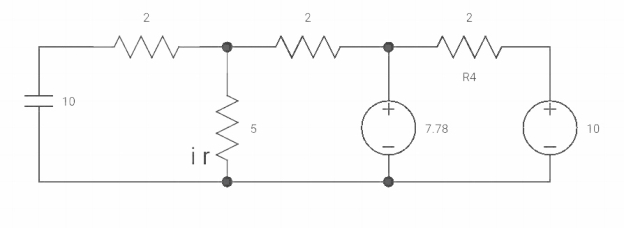
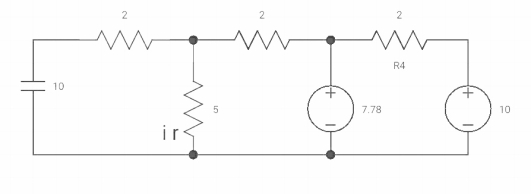
$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_190932.jpg$

Vc(o+) and iR (o+) it switches ‘s’ is closed at t=0?

At t=0

$C:\Users\TARUNA\Desktop\qq\5.JPG$

As capacitor is fully charged so acts as

Vc (0-) = 7*10/7+2 = 70/9v

At t=0+

$C:\Users\TARUNA\AppData\Local\Microsoft\Windows\Temporary Internet Files\Content.Word\IMG_20191229_191007.jpg$

Vc (0+) = Vc (0) = 40/9v

By applying kcl at A,

VA-10/2+ VA/5+VA-7019/2 =0

VA [1/5+1/2+1/2] = 5+35/9

Va [6/5] = 80/9

Va= 400/54v

IR (0+) = Va/5 = 400/54*5 = 80/54 A

Reference Books

D. P. Kothari and I. J. Nagrath, “Basic Electrical Engineering”, Tata Mcgraw Hill, 2010.
D. C. Kulshreshtha, “Basic Electrical Engineering”, Mcgraw Hill, 2009.
L. S. Bobrow, “Fundamentals Of Electrical Engineering”, Oxford University Press, 2011.
E. Hughes, “Electrical And Electronics Technology”, Pearson, 2010.
V. D. Toro, “Electrical Engineering Fundamentals”, Prentice Hall India, 1989.
Basic Electrical Engineering by Fitzerald, Et Al, Tata Mcgraw Hill
Fundamentals of Electrical Engg. By R. Prasad, Phi Publication
Basic Electrical Engineering by V.K. Mehta And Rohit Mehta, S.Chand Publication

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined