Unit – 3
Magnetic Circuit
It involves the interaction of magnetic field and current carrying conductor placed in it. The operation sequence is as follow
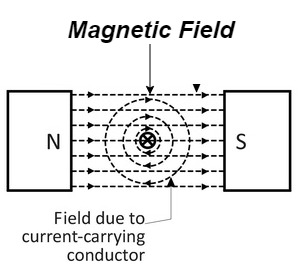
2. Interaction of two magnetic field
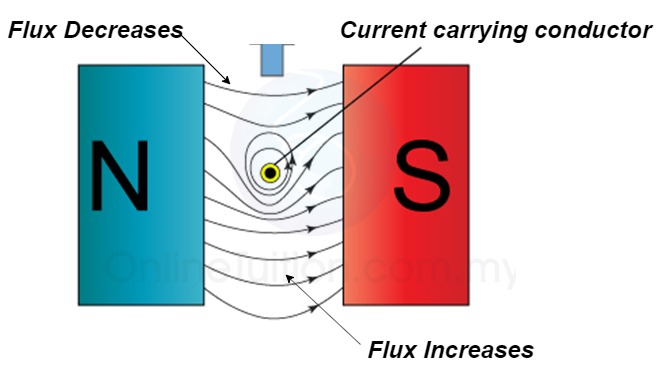
At the top flux lines produced by the magnet and conductor are in opposite direction to each other and hence cancel each other.
At the bottom individual fields are in same direction they will add each other.
3. Force excreted on the conductor
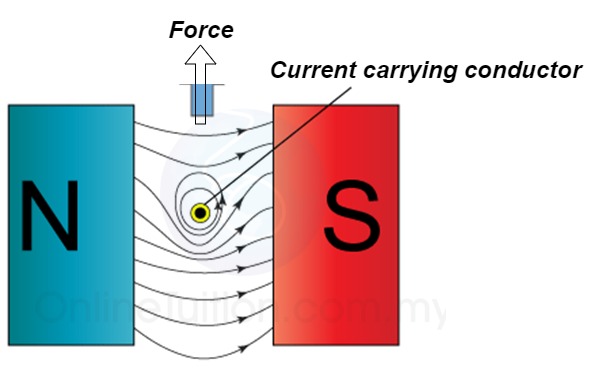
The lines of force on the bottom exert a force on the conductor in the upward direction as shown above.
Hence mechanical force is exerted on the conductor from high flux line area towards the low flux line area (top).
The magnetically of force experienced by the current carrying conductor placed in a magnetic field is given by
F = B I ɺ sin Ɵ newton
Where F = Force exerted
B = Flux density
ɺ = length of conductor
I = current
Ɵ = angle between conductor and magnetic field.
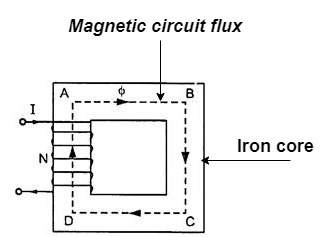
The magnetic circuit can be defined asthe closed path traced by magnetic lineof forcesuch magnetic circuit is associated with different magnetic quantities such as MMF, flux, flux density, magnetic field strength
we know that H =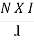 
and B = μ H
put value of H
B = μ x 
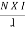
But μ = μₒ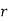μ
B = μ₀μ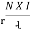
But B =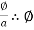 
= B x a
Ø =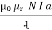
Numerical on F = B I ɻ sin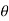 
Series Magnetic Circuits
Derivation of series magnetic current with air gap
In series magnetic circuit flux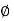 
is same in each part of circuit
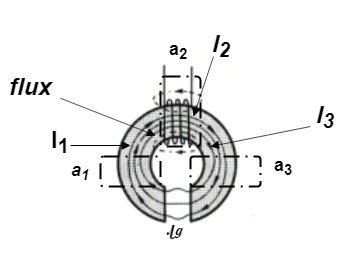
Consider a composite magnetic circuit made from different material of lengths ɻ1,ɻ2, and ɻ3 cross sectional area a1, a2 And a3 and relative permeability’s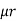 
1 , 
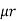2 ,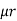 
3 resp. with an airgap of length ɻɡ
Parallel Magnetic Circuits
A magnetic circuit which has more than one path for flux called parallel magnetic circuit
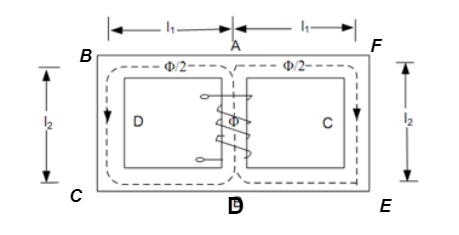
Mean length ABCDA = ɻ₁, and ADEFA = ɻ₂
Mean length path for central limb = ɻc
Reluctance ABCDA = S1, ADEFA = S2
And central limb = SC
Now total mmȴ = N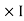 
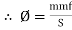i.e. mmf =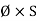 
Derivation of series magnetic current with air gap
In series magnetic circuit flux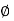 
is same in each part of circuit
Consider a composite magnetic circuit made from different material of lengths ɻ1,ɻ2, and ɻ3 cross sectional area a1, a2 And a3 and relative permeability’s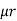 
1 , 
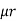2 ,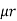 
3 resp. with an airgap of length ɻɡ
Total reluctance S = S1 + S2+ S3 + Sg
We know that S =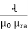 
+ 
+ 
+ 
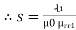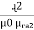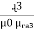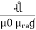
But S =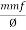 
and mmf = S x Ø
mmf = Ø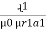
+ 
+ 
+ 
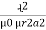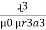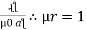for air
Now B =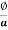 
mmȴ =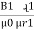 
+ 
+ 
+ 
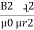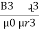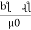
but B=μH
H = 
= 
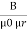
Total mmȴ = H1 ɻ1+ H2 ɻ2 + H3 ɻ3 + Hƪɻƪ
A magnetic circuit which has more than one path for flux called parallel magnetic circuit
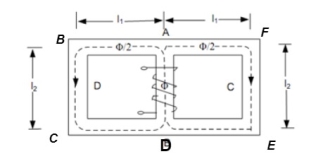
Mean length ABCDA = ɻ₁, and ADEFA = ɻ₂
Mean length path for central limb = ɻc
Reluctance ABCDA = S1, ADEFA = S2
And central limb = SC
Now total mmȴ = N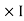 
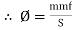i.e. mmf =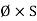 
For path ABC AD
N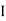 
= 
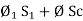
where S1 =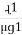
, S2 = 
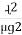, and Sc =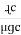 
where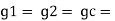 
area of cross selection
for parallel ekt.
Total mmȴ = mmȴ by central limb + mmȴ required by any one of outer limb
= Ø sc + [Ø1S1 or Ø2 S2]
As mmf across parallel branch is same
Ø1 S1 = Ø2 S2
Hence while calculating total mmf, the mmf of only one of 2 parallel branches must be considered.
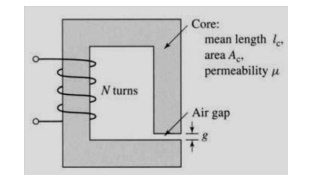
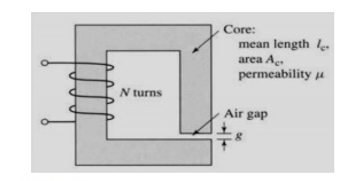
A magnetic circuit with a single air gap is shown in Figure. The core dimensions are:
Cross-sectional area Ac = 1.8 × 10-3 m2
Mean core length lc = 0.6 m
Gap length g = 2.3 x 10-3 m
N = 83 turns
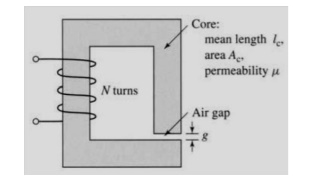
Assume that the core is of infinite permeability ( m -> ¥) and neglect the effects of fringing fields at the air gap and leakage flux.
(a) Calculate the reluctance of the core Re and that of the gap Rg. For a current of i = 1.5 A,
(b) calculate the total flux ϕ
(c) the flux linkages λ of the coil,
(d) the coil inductance L.
Solution:
Rc=0 since μ -> ∞
Rg = g/ μo Ac = 2.3 x 10 -3 / 4 π x 10 -7 x 1.8 x 10 -3 = 1.017 x 10 6 A/Wb
ɸ = Ni/ Rc + Rg = 83 x 1.5 / 1.017 x 10 6 = 1.224 x 10 -4 Wb
λ = N ɸ = 1.016 x 10 -2 Wb
L = λ/I = 1.016 x 10 -2 / 1.5 = 6.773mH
Example. No.2
Consider the magnetic circuit of with the dimensions of Problem 1.1. Assuming infinite core permeability, calculate (a) the number of turns required to achieve an inductance of 12 mH and (b) the inductor current which will result in a core flux density of 1.0 T.
Solution:
L = N 2 / Rg = 12 x 10 -3 mH => √ 12 x 10 -3 x 1.017 x 10 6 = 110.47
N= 110 turns
Bc = Bg =1.0 T
ɸ= Bg Ac = 1.8 x 10 -3 Wb
i= λ/L = Nɸ/L = 110 x 1.8 x 10 -3 / 12 x 10 -3 = 16.5 A
Example:
In the magnetic circuit as shown in figure (a) the relative permeability of the ferro magnetic material is 1200. Neglect the magnetic leakage and fringing. All dimensions are in centimetres, and the magnetic material has a square cross- sectional area. Determine the air gap flux , air gap flux density and the magnetic field intensity in the air gap.
Solution
The mean magnetic path of the fluxes are shown by dashed lines in figure(a) The equivalent magnetic circuit is shown in figure(b).
F1 = N1 I1 = 500 x 10 = 5000 At
F2 = N2 I2 = 500 x 10 = 5000 At
μc= 1200 μo = 1200 x 4π x 10 -7
Rbafe = l bafe/ μc Ac
= 3 x 52 x 10 -2 / 1200 x 4π x 10 -7 x 4 x 10-4
= 2.58 x 10 6 At/Wb
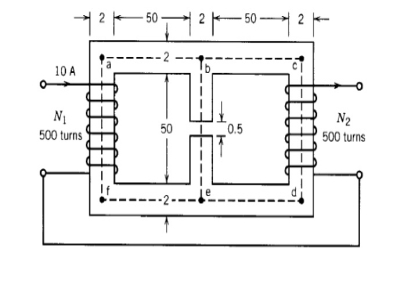
From symmetry
Rbcde = R bafe
Rg = lg / μo Ag
= 5 x 10 -3 / 4π x 10 -7 x 2 x 2 x 10 -4
Rbe(core) = lbe(core) / μc Ac
= 51.5 x 10 -2 / 1200 x 4π x 10 -7 x 4 x 10 -4
= 0.82 x 10 6 At/Wb
The loop equations are
ɸ1(13.34 x 10 6) + ɸ2 (10.76 x 10 6) = 5000
ɸ1(10.76 x 10 6) + ɸ2 (10.76 x 10 6) = 5000
The air gap flux density is
Bg = ɸg/Ag = 4.134 x 10 -4 / 4 x 10 -4 = 1.034 T
The magnetic intensity in the air gap is
Hg = Bg / μo = 1.034/ 4π 10 -7 = 0.822 x 10 6 At/m
For the magnetic circuit of the above figure N =400 turns.
Mean core length lc= 50 cm
Air gap length = 1.0 mm
Cross sectional area Ac = Ag = 15 cm2
Relative permeability of core μr = 3000
i = 1.0A
Find
(a) Flux and flux density in the air gap
(b) Inductance of the coil.
Solution:
Rc = lc / μr .μo. Ac = 50 x 10 -2 / 3000 x 4π x 10 -7 x 15 x 10 -4
= 88.42 x 10 3 AT/Wb
Rg = lg / μo Ag = 1 x 10 -3 / 4 π x 10 -7 x 15 x 10 -4
= 530.515 x 10 3 AT/Wb
ɸ = Ni/ Rc + Rg
= 400 x 1.0 / (88.42 + 530.515 ) 10 3
B = ɸ/Ag = 0.6463 x 10 -3 / 15 x 10-4 = 0.4309
L = N2 / Rc + Rg = 400 2 / (88.42 + 530.515) 10 3
= 258.52 x 10 -3 H
Or
L = λ/i = Nɸ/i = 400 x 0.6463 x 10 -3 / 1.0 = 258.52 x 10 -3 H
References:
