Module 1
Waves
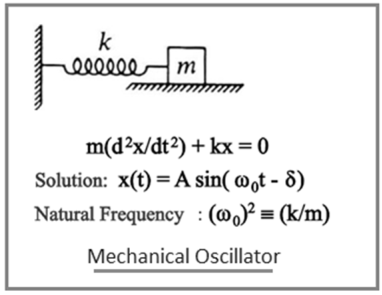
The figure depicts simple mechanical oscillator having mass attached to the spring. This structure is similar to Pendulum. It is also known as harmonic oscillator
If a body attached to a spring is displaced from its symmetry position, the spring applies a restoring force on it, which tends to bring back the object to the equilibrium position. This force roots oscillation of the system, or periodic motion.
f =
, where "T" and "f" are period of oscillation and frequency of the oscillation.
Angular frequency is about 2π times of frequency i.e.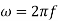 
When the restoring force is directly proportional to the displacement from equilibrium, the resulting motion is known as simple harmonic motion and the oscillator is known as Harmonic Oscillator.
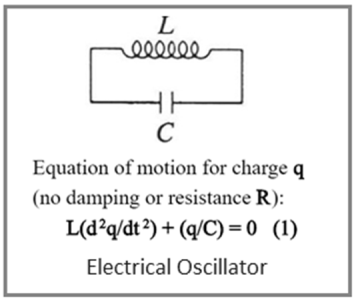
The figure depicts electrical analogy of the mechanical oscillator. This is example of electronic or electrical oscillator. There are different types of oscillators viz. RC oscillator, LC oscillator, crystal oscillator etc.
LC circuit is made from an inductor and a capacitor. Originally capacitor is charged and a current is induced in the inductor. After this current and voltage oscillate harmonically according to following equation.
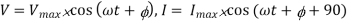Let us develop differential equation to represent electrical oscillator.
Capacitor discharges (or charges) through inductor, Hence current (I) in inductor and charge (Q) on capacitor are related as
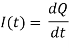
Therefore, voltage on inductor is related to second time derivative of the charge as
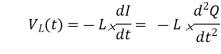Nevertheless, in LC circuit, voltage on inductor must be same as voltage on the capacitor,
Hence, VL = VC = Q/C
Comparing the last two equations, we can get,
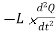= VL(t) = VC(t)=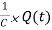 
This is second order differential equation for Q has form of harmonic oscillator.
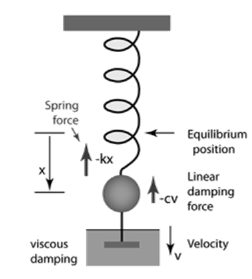
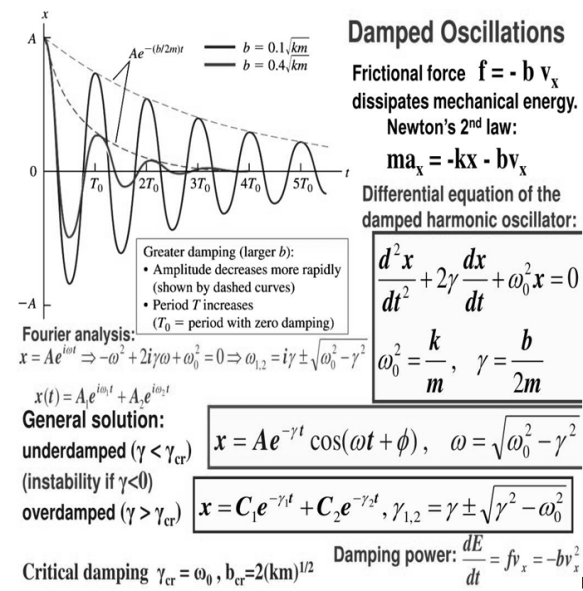
When the motion of an oscillator decreases due to an external force, the oscillator and its wave are damped.
These periodic motions of slowly decreasing amplitude are damped simple harmonic motion.
An example of a damped simple harmonic wave is a simple pendulum.
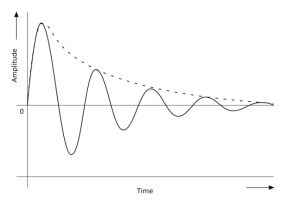
In the damped simple harmonic motion, the energy of the oscillator dissipates limitlessly. But for a small damping, the oscillations remain about periodic. The forces which scatter the energy are typically frictional forces.
The Newton's IInd Law of motion equation is
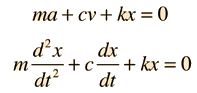
This is in the form of a homogeneous second order differential equation and has a explanation of the form
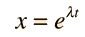
Replacing this form gives asecondary equation for λ
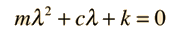
The roots of the quadratic secondary equation are
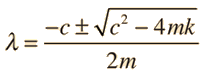
The three resultant cases for the damped oscillator are
When a damped oscillator is subjected to damping force which is dependent upon velocity (v), like a viscous damping, the wavering will must exponential decay (negative sign in equation we can say) place which be subject to damping factor(c). If the damping force is of the form
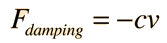
Then the damping coefficient is given by
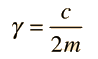
This will appear logical when you note that the damping force is relative to c, but its influence in reverse proportional to the mass of the oscillator.
Ist Law for Simple Harmonic Motion (S.H.M.)
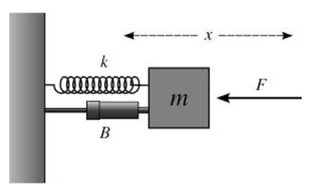
Let’s develop the force law for simple harmonic motion (S.H.M.) with an example. A spring-block system is the simplest sample of simple harmonic motion. Consider a block of mass (m) attached to a spring, which in turn is fixed to aninflexible wall. The block rests on a frictionless surface. When we do not pull the spring, that is, no force is functional on it, it is in its stabilityposition. In this state, the overall force acting on it is zero. Now, let’s make two actions and observe what happens.
When we pull the block out, there is a force acting on the block that attempts to pull it in, that is, near its equilibrium position.
When we push the block in, there is a force acting on the block attempts to push it out, that is, near its equilibrium position.
In both the cases, we can see that there is a force acting on the block that attempts to return the block to its equilibrium position. This force is the restoring force(F) and the force law for simple harmonic motion (S.H.M.) is based on this force. Let’s learn how to calculate this law.
Derivation of Force Law for Simple Harmonic Motion,
Let the restoring force be F and the movement of the block from its equilibrium position be x. Thus, from the cases we detected, we can say that the restoring force(F) is directly proportional to the displacement(x) from the mean position.
∴ F = – kx
Here k is a constant known as the force constant. Its unit is N/m in S.I. System and dynes/cm in C.G.S. System. The -ve sign indicates that the restoring force and the displacement are always in reverse direction.
The above equation is the simplest form of force law for simple harmonic motion. It proves the basic rule of simple harmonic motion, that is, force and displacement should be in reverse direction.
Further, we know that F = ma.
Therefore, a = F/m.
Replace F= -kx, we get,
a = – kx/m = – ω2x (where k/m = ω2)
Above equation is known as force law of simple harmonic motion (S.H.M.). Note that the restoring force is always near the mean position and in the reverse direction of that of displacement.
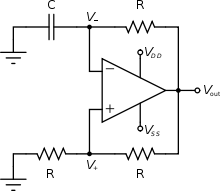
An electronic oscillator is an electronic circuit that produces a periodic oscillating electronic signal regularly a sine wave or a square wave.
Oscillators convert direct current (DC) from a power supply to an alternating current (AC) signal. Electronic oscillator isused in many electronic equipment ranging after simplest clock producers to digital instruments,similar calculators and complex computers and peripherals etc.
Common examples of signals generated by oscillators include signals broadcast by radio and television transmitters, clock signals that regulate computers and quartz clocks, and the sounds produced by electronic beepers and video games.
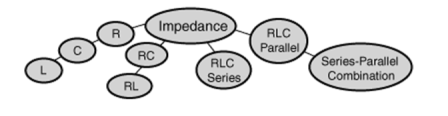
Ohm's Law applies directly to resistors in DC (Direct current) or in AC (Alternating current) circuits, the form of the current-voltage (CV) relationship in AC circuits in general is modified to the form:
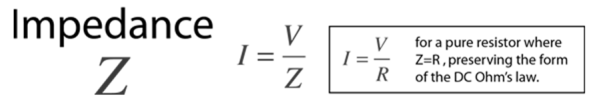
Where I and V are the rms (root mean square) or effective values. The symbol Z is called impedance. For a pure resistor, Z = R.
Since, the phase traces the impedance and since the contributions of capacitors(C) and inductors(L) differ in phase from resistive components by 900, a process like vector addition (phasors) is used to develop terms for impedance. More general is the complex impedance method.
If a damped oscillator is determined by an external force, the result to the motion equation has 2 parts, a transient part and a steady-state part, which must be used composed to fit the physical boundary circumstances of the problem. The early behavior of a damped, driven oscillator can be quite complex.
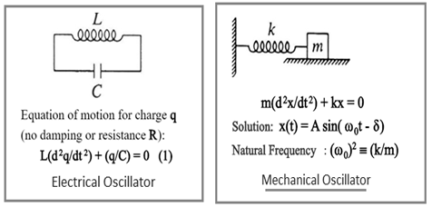
The figure depicts electrical analogy of the mechanical oscillator. This is example of electronic or electrical oscillator. There are different types of oscillators viz. RC oscillator, LC oscillator, crystal oscillator etc.
LC circuit is made from an inductor and a capacitor. Originally capacitor is charged and a current is induced in the inductor. After this current and oltage oscillate harmonically according to following equation.
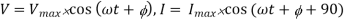Let us develop differential equation to represent electrical oscillator.
Capacitor discharges (or charges) through inductor, Hence current (I) in inductor and charge (Q) on capacitor are related as
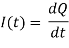
Therefore, voltage on inductor is related to second time derivative of the charge as
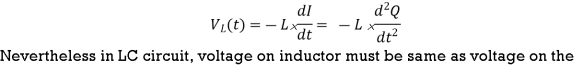Hence, VL = VC = Q/C
Comparing the last two equations, we can get,
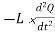= VL (t) = VC (t)=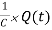 
This is second order differential equation for Q has form of harmonic oscillator.
Let the restoring force be F and the movement of the block from its equilibrium position be x. Thus, from the cases we detected, we can say that the restoring force(F) is directly proportional to the displacement(x) from the mean position.
∴ F = – kx
Here k is a constant known as the force constant. It’s unit is N/m in S.I. System and dynes/cm in C.G.S. System. The -ve sign indicates that the restoring force and the displacement are always in reverse direction.
The above equation is the simplest form of force law for simple harmonic motion. It proves the basic rule of simple harmonic motion, that is, force and displacement should be in reverse direction.
Further, we know that F = ma.
Therefore, a = F/m.
Replace F= -kx, we get,
a = – kx/m = – ω2x (where k/m = ω2)
Above equation is known as force law of simple harmonic motion(S.H.M.). Note that the restoring force is always near the mean position and in the reverse direction of that of displacement.
An electronic oscillator is an electronic circuit that produces a periodic oscillating electronic signal regularly a sine wave or a square wave.
Oscillators convert direct current (DC) from a power supply to an alternating current (AC) signal. Electronic oscillator areused in many electronic equipment ranging after simplest clock producers to digital instruments, similar calculators and complex computers and peripherals etc.
Common examples of signals generated by oscillators include signals broadcast by radio and television transmitters, clock signals that regulate computers and quartz clocks, and the sounds produced by electronic beepers and video games.
