UNIT 2
NON-DISPERSIVE TRANSVERSE AND LONGITUDINAL WAVES
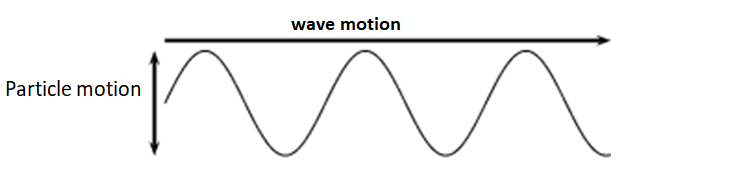
Assume you are holding one side of a string and the other side is fixed and the string is pulled fitted.
Vibrate the string up and down. The wave that developed due to this vibration is called a transverse wave.
The wave in which the direction of disturbance is perpendicular to the direction of travelling wave.
The above diagram show that propagation takes place in the rope. The wave travelled from one end to the other while the rope moved up and down.
Speed of a Wave on a String
Velocity= distance travelled/Time
In waves: Velocity can be found by dividing the wavelength(λ) by the period(T):
v=λ/T We can take the inverse proportionality to period(T) and frequency(λ) and apply it,
v=λ/T
v=λ1/T
v=λf
Speed of a Wave on a Vibrating String
- In musical instruments we can find wave in vibrating string like Keyboard and guitar.
- In these cases, the frequency is what characterizes the pitch and therefore the note.
- The rapidity of a wave on this kind of string is proportional to the square root of the tension(T) in the string and inversely proportional to the square root of the linear density of the string:v=√T/μ
The wave equation for a plane wave traveling in the x- direction which is
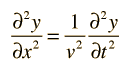
Here, v is the phase velocity of the wave and y represents the variable which is changing as the wave passes.
This is the method of the wave equation which applies to a stretched string or a plane electromagnetic (EM) wave.
The mathematical description of a wave makes use of partial derivatives.
In 2 dimensions, the wave equation takes the form
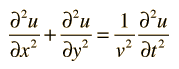
Whichmight describe a wave on a stretched membrane.
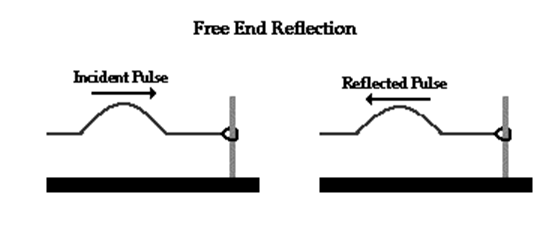
Reflections
When transverse waves in strings meet one end they get reflected and when the incident wave meets the reflected wave, interference happens.

A harmonic wave is a wave with a frequency () that is a +ve integer of variousfrequency () of the unique wave, known as the fundamental frequency. The unique wave is also called the 1st harmonic, the subsequent harmonics are known as higher harmonics.
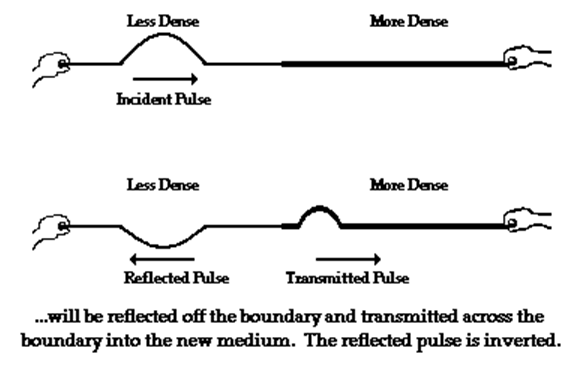
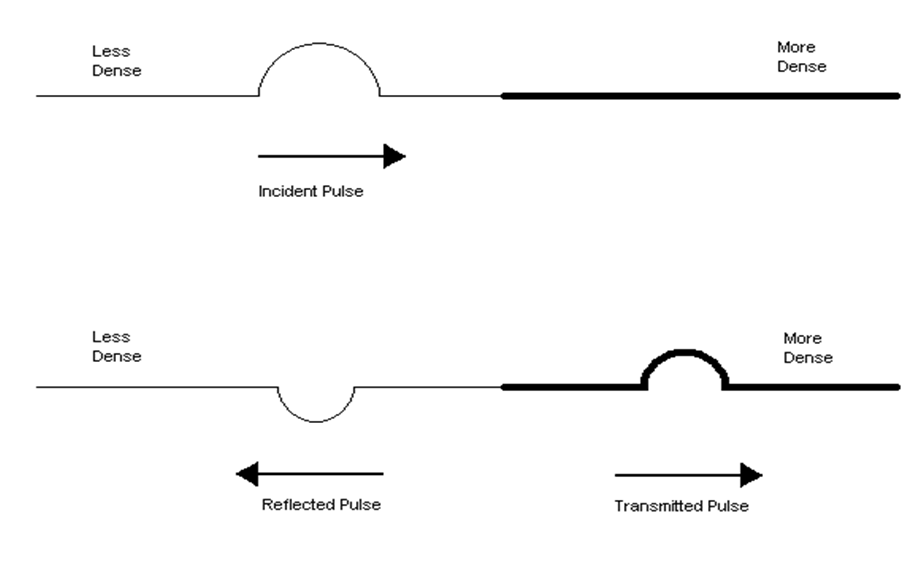
In different two media there is reflection and transmission.
Reflected wave are those who come back to the original position after reflection from boundary
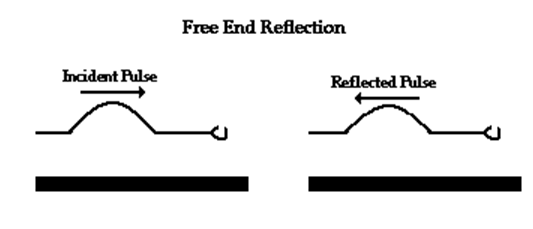
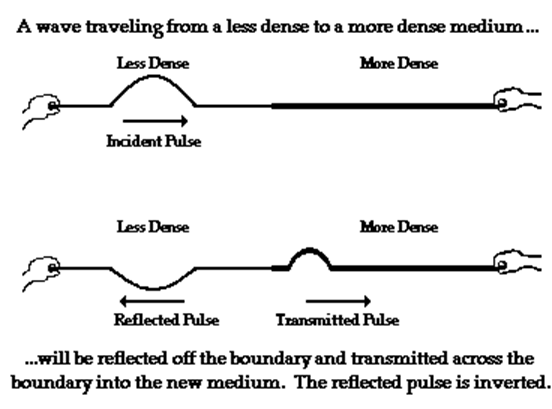
Assume thin rope attached to a thick rope with each rope held at opposite ends by people. And suppose that a vibration is introduced by the person holding the end of the thin rope then vibration travel from thin end to thick end.

Upon reaching the boundary, the usually two behaviours will happen.
The wave which come back to the initial position are known as reflected wave.
The vibration which goes to thick end after vibrating to the rope known as transmitted pulse.
The reflected vibration will be found to be inverted. During the interaction between the two mediums at the boundary, the Ist particle of the more dense medium defeats the smaller mass of the last particle of the less dense medium.
This causes an upward displaced pulse to become a downward displaced pulse.
The denser medium on the other hand was at rest prior to the interaction. The Ist particle of this medium receives an upward pull when the incident pulse touches the boundary.
Since, the denser medium was initially at rest, an upward pull causes an upward displacement.
Meanwhile the particles in this medium are initially at rest, any change in their state of motion would be in the similar direction as the displacement of the particles of the incident pulse.
Some of the most exciting impedance matching occurs when energy comes in the form of a wave. Meanwhile there is an impedance mismatch between the water and the wall, the wave energy is unable to couple into the wall, and so it reflects back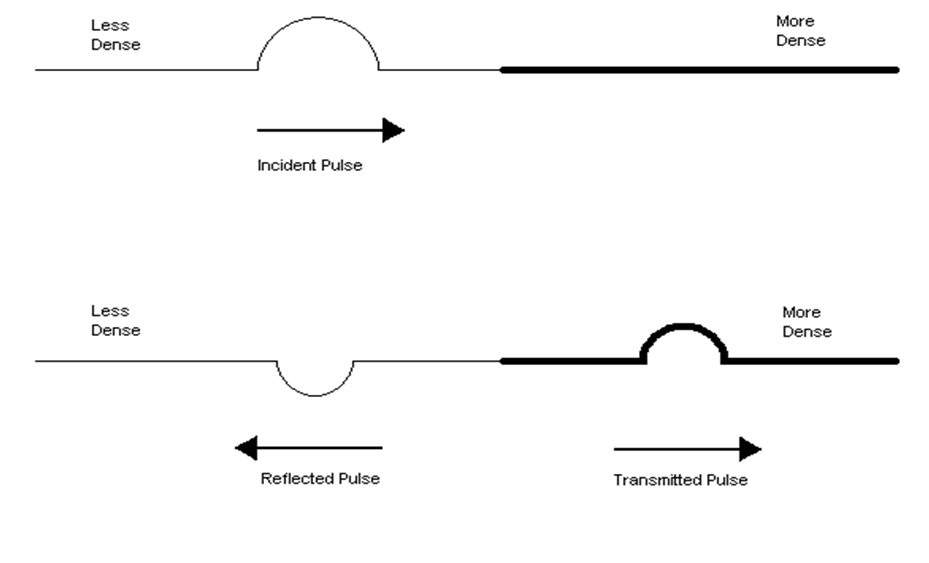
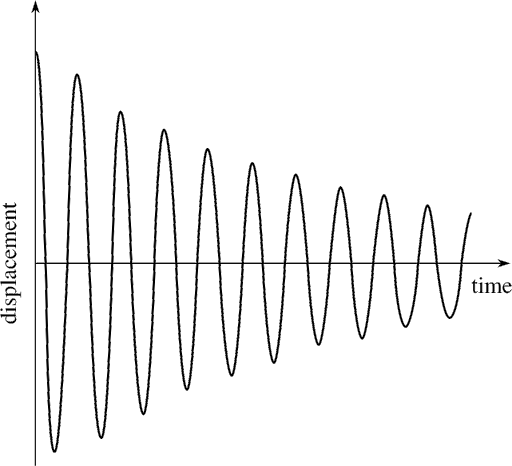
Standing waves are always associated with resonance. Resonance can be recognized by anintense increase in amplitude of the resultant vibrations.
Any system in which standing waves can form has numerous natural frequencies. The set of entirely possible standing waves are known as the harmonics of a system.
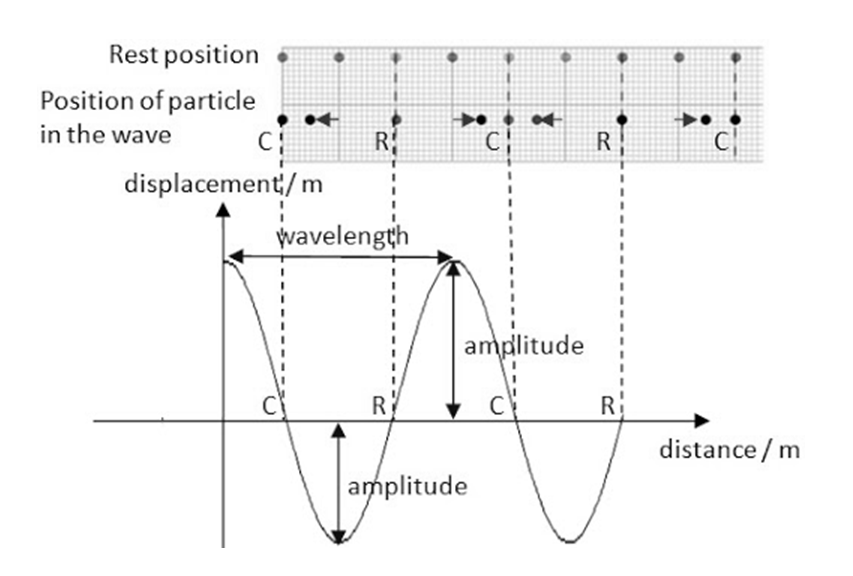
x is the distance the point traveled from the wave's source.
t is the time elapsed.
y0 is the amplitude of the oscillations.
c is the speed of the wave.
Natural frequency isalso known as eigenfrequency. Eigen frequency is that frequency at which a system tends to oscillate in the absence of any driving or damping force.
The motion pattern of a system oscillating at its natural frequency is called the regular mode.
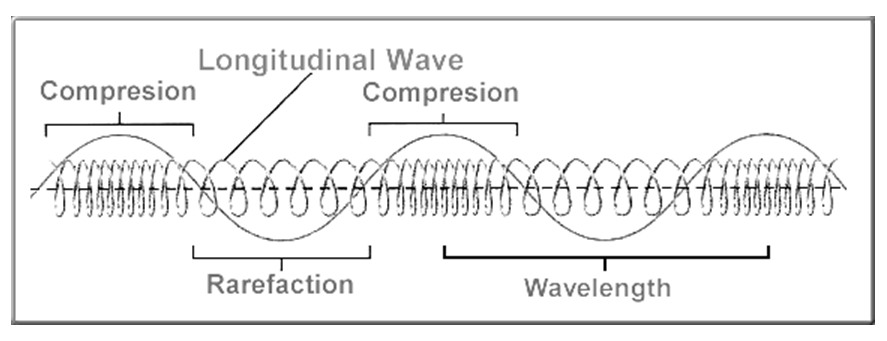
Longitudinal Wave Formula
y (x, t) =y0cos[ω(t−xc)]
Where,
y = displacement of the point on the traveling sound wave
x =distance the point traveled from the wave’s source
t =time elapsed
y0 = amplitude of the oscillations
c = speed of the wave
ω =angular frequency of the wave
x/c = (t) (time wave takes to travel the distance x).
Frequency (f) of the wave is given by the formula:
f=ω2π
Acoustic waves are a type of energy propagation over a medium by means of adiabatic compression besides decompression. Significant quantities for relating acoustic waves are acoustic pressure, particle velocity, particle displacement and acoustic intensity.
Acoustic waves travel with a typical acoustic velocity that depends on the medium they're transitory through.
Some instances of acoustic waves are audible sound from a speaker (waves traveling through air at the speed of sound), ground movement from an earthquake (waves traveling through the earth), or ultrasound used for medical imaging (waves traveling through the body).
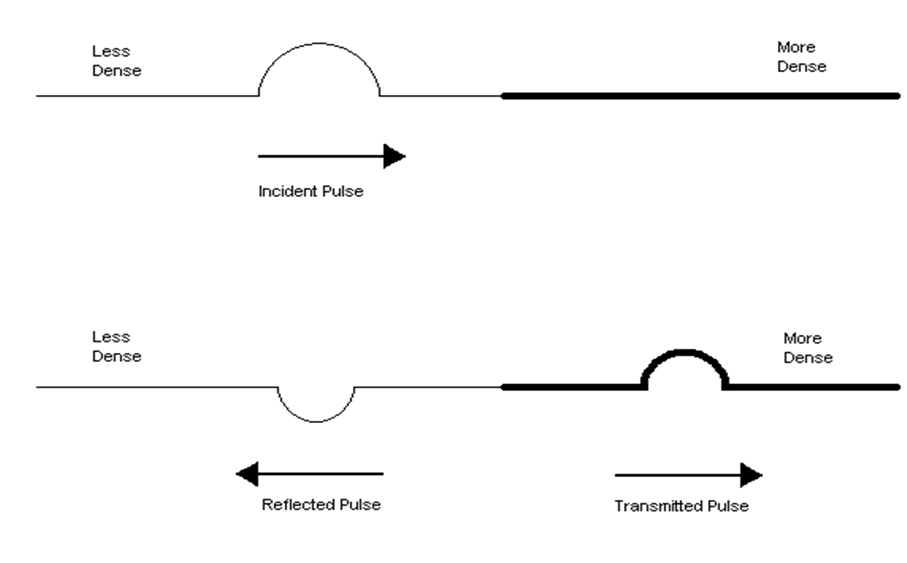
In different two media there is reflection and transmission.
Reflected wave are those who come back to the original position after reflection from boundary
Assume thin rope attached to a thick rope with each rope held at opposite ends by people. And suppose that a vibration is introduced by the person holding the end of the thin rope then vibration travel from thin end to thick end.

Upon reaching the boundary, the usually two behaviours will happen.
The wave which come back to the initial position are known as reflected wave.
The vibration which goes to thick end after vibrating to the rope known as transmitted pulse.
The reflected vibration will be found to be inverted. During the interaction between the two medium at the boundary, the Ist particle of the more dense medium defeats the smaller mass of the last particle of the less dense medium.
This causes an upward displaced pulse to become a downward displaced pulse.
The more dense medium on the other hand was at rest prior to the interaction. The Ist particle of this medium receives an upward pull when the incident pulse touches the boundary.
Since, the more dense medium was initially at rest, an upward pull cause an upward displacement.
Meanwhile the particles in this medium are initially at rest, any change in their state of motion would be in the similar direction as the displacement of the particles of the incident pulse.
Some of the most exciting impedance matching occurs when energy comes in the form of a wave. Meanwhile there is an impedance mismatch between the water and the wall, the wave energy is unable to couple into the wall, and so it reflects back.
Standing waves are always associated with resonance. Resonance can be recognized by a intense increase in amplitude of the resultant vibrations.
Any system in which standing waves can form has numerous natural frequencies. The set of entirely possible standing waves are known as the harmonics of a system.
x is the distance the point traveled from the wave's source.
t is the time elapsed.
y0 is the amplitude of the oscillations.
c is the speed of the wave.
Some of the most exciting impedance matching occurs when energy comes in the form of a wave. Meanwhile there is an impedance mismatch between the water and the wall, the wave energy is unable to couple into the wall, and so it reflects back.
Reference:
1. G. MAIN, “VIBRATIONS AND WAVES IN PHYSICS”, CAMBRIDGE UNIVERSITY PRESS,1993.
2. H. J. PAIN, “THE PHYSICS OF VIBRATIONS AND WAVES”, WILEY, 2006.
3. E. HECHT, “OPTICS”, PEARSON EDUCATION, 2008.
4. A. GHATAK, “OPTICS”, MCGRAW HILL EDUCATION, 2012.
5. O. SVELTO, “PRINCIPLES OF LASERS”, SPRINGER SCIENCE & BUSINESS MEDIA, 2010.