Unit – 1
Atomic And Molecular Structure
Black-body radiation is a thermal electromagnetic radiation inside or surrounding a body in thermodynamic state with its environment, emitted by a black body (an idealized opaque, non-reflective body). It has a very specific spectrum of wavelengths, inversely related to intensity that is dependent only on the body's temperature, it is assumed for calculations and theory to be uniform and to be constant.
Classical physics failed to explain Black body spectrum of radiation over all frequency ranges, which came to be known as catastrophe. There was an incongruency between theory and experiment. Classically, the radiant energy density dρ was described in the following equation:
dρ (v, T) =8KBTv2dv/c3
As the frequency of light increases the radiant energy density approaches infinity is shown in Figure 1. However, this phase was not observed in the experiments. however, the radiant energy density was found to decrease as the frequency increased in the UV spectrum.
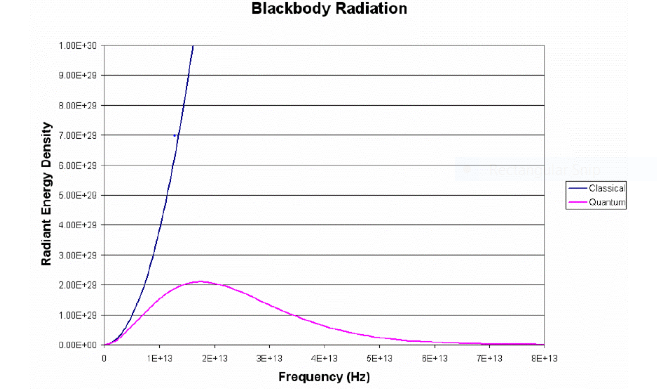
Fig 1. A comparison of the classical and the quantum models of Black body Radiation
The Quantum values agrees with the experimental values, whereas the classical model diverges at high frequencies. This high frequency divergence is what is referred to as the UV catastrophe. Notice that as the frequency of radiation decreases, the quantum prediction moves towards the classical prediction.
In 1900, Max Planck successfully explained the blackbody radiation, and derived the following equation to accurately to describe the experimental results.
Planck was able to derive this equation by assuming that the energy of the oscillators was quantized. (E=nhv, where h is the Planck’s constant = 6.626x10-34 J-s). Planck’s quantization of energy was a revolutionary that marked the beginning of a new field of quantum physics.
Photoelectric effect:
Another phenomenon in which quantum physics approach was used to explain the experimental results in the photoelectric effect. Classical/Newtonian physics describes light as a wave (electromagnetic radiation) which has a set frequency and amplitude where the amplitude is related to intensity. Light was observed to cause electrons to be ejected from a metal surface.
Einstein modified Planck’s concept of quantization of energy to describe the experimental results.
Einstein proposed that light can travel in small quantized packets of energy (photons) instead of s behaving as classical wave. Einstein showed that the kinetic energy of the ejected electrons is equal to the energy of the incident photon minus the energy barrier to releasing an electron from that particular metal. This interpretation is described by the following equation:
KE=1/2mv2=hv-ⱷ
This model was able to account for the experimental results including the lack of dependence of the energy of the photons that are ejected on the intensity of the incident radiation as well as the failure of some frequencies of light to eject any photons (the incident energy of the photon was less than the work function of the metal).
Electromagnetic radiation is energy that is promote through free space or through a substance medium in the form of electromagnetic waves, such as radio waves, visible light, and gamma rays. This term also refers to the emission and transmission of such radiant energy.
The Scottish physicist James Clerk Maxwell was the first to estimate the existence of electromagnetic waves. In 1864 he set forth his electromagnetic theory, proposing that light-including various other forms of radiant energy-is an electromagnetic disturbance in the form of waves. In 1887 Heinrich Hertz, a German physicist, provided ample experimental confirmation by producing the first man-made electromagnetic waves and discover their properties. Subsequent studies resulted in a broader understanding of the nature and origin of radiant energy.

Fig.2 Corelation of Electric and Magnetic Fields
It has been established that time-varying electric fields can induce magnetic fields and that time-varying magnetic fields can similarly induce electric fields. Because such electric and magnetic fields generate together, they occur jointly, and together they can propagate as electromagnetic waves. An electromagnetic wave is a transverse wave in that the electric field and magnetic field at any point and time in the wave are perpendicular to each other as well as to the direction of propagation. In a given free space (i.e., a space that is absolutely devoid of matter and that experiences no intrusion from other fields or forces), electromagnetic waves always propagate with the same speed—that of light (299,792,458 m per second)—independent of the speed of the observer or of the source of the waves.
The dual nature of electromagnetic waves refers to the fact that, electromagnetic waves act both like a wave and particle. Electromagnetic radiation has found to be basically light which is present in a rainbow,
It is also a spectrum consisting of radio waves, infrared waves, visible light, ultraviolet radiation, X-rays and gamma rays. There are only two ways to transfer energy from one place to another
An electromagnetic radiation is a particle and also a wave, thus it makes it interesting to study its nature in quantum theory. Light is also an electromagnetic radiation which contain frequencies.
The photoelectric effect could be explained considering that radiations consist of small packets of energy can be treated as particles. On the other hand, radiations exhibit a phenomenon of interference and diffraction which indicates that they possess wave nature. So, it can be concluded that electromagnetic radiations possess dual nature.
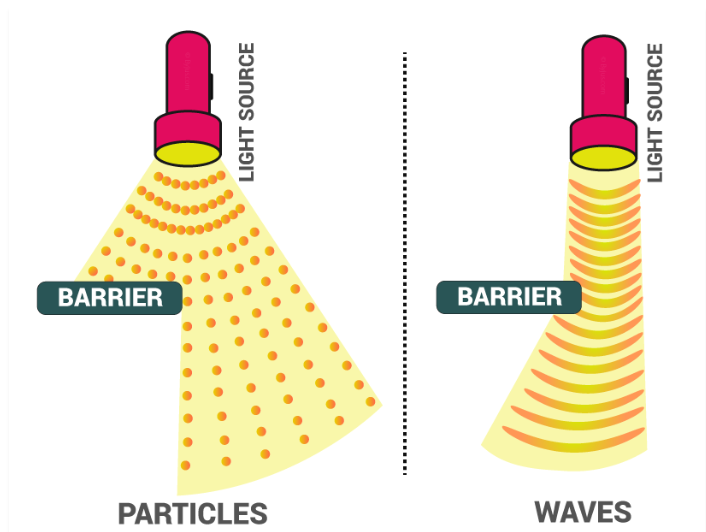
Fig. 3: Effects of particle and wave on a light source.
According to Planck’s quantum theory, the smallest amount of energy that can be emitted or absorbed in the form of electromagnetic radiation is known as quantum. The energy of electromagnetic radiation absorbed or emitted is directly proportional to the frequency of the radiation.
Planck postulated that the energy of an electromagnetic radiation is proportional to the frequency of the radiation-the higher the frequency the greater the energy. This is written as the formula below and called as Planck’s Equation:
h: Planck’s constant has a value of 6.626x10-34 J-s.
E=hv
Planck’s quantum theory
According to Planck’s quantum theory,
1.Different atoms and molecules can emit or absorb energy in discrete quantities only. The smallest or minute amount of energy that can be emitted or absorbed in the form of electromagnetic radiation is known as its measure or quantum.
2.The energy of the radiation absorbed or emitted is directly proportional to the frequency of the radiation.
Meanwhile, the energy of radiation is expressed in terms of frequency as,
E=hv
Where,
E= Energy of the radiation
h= Planck’s constant (6.626x10-34 J-s)
v= Frequency of radiation
Planck has also concluded that these were only an aspect of the processes of absorption and emission of radiation.
The photoelectric effect is the emission of electrons or other free carriers when electromagnetic radiations, like light hits on a material, electrons emitted in this manner can be called photoelectrons below the threshold, no electrons are given out from the material or source, without any regard to the light intensity or the length of time to the exposure to the light. The photoelectric effect can be assigned to the transfer of energy from the light to an electron. From this prospective, an alteration in the intensity of the light induces changes in the kinetic energy of the electrons emitted from the metal. As the frequency is of low intensity it could not build up the energy required to produce the photoelectrons, like it would have if light energy was a continuous wave. Few experiments proved that electrons are dislodged only by the impingement of light when it reached or exceeded a threshold frequency. Below that threshold, no electrons are emitted from the material, regardless of the light intensity or the length of time of exposure to the light.
Failure of uncertainty of Heisenberg principle
It was Articulated in 1927 by the German physicist Werner Heisenberg, according to him the position and velocity of an object cannot be measured exactly, at the same time, even in theory.
Para magnetism is a form of magnetism where certain materials or sources are attracted by an external applied magnetic field. Valence bond theory (VBT) and hybridisation does not clearly explain the prediction of whether a molecule is paramagnetic or diamagnetic (is not attracted by an external magnetic field). This is why molecular orbital theory (MOT) is so useful as it is successful in predicting whether a molecule is paramagnetic or not.
For a molecule to be paramagnetic, it needs to have an overall magnetic moment meaning that it needs an unpaired electron. If all the electrons are paired, then the molecule is diamagnetic. So, by seeing whether a molecule has an unpaired electron, we can predict if it is paramagnetic or not.
Now let’s consider the example of O2OX2. Experimentally, O2OX2 is known to paramagnetic. According to VBT, O2OX2 should look like this:

Fig 4: Paramagnetic property of molecules.
As you can see, all the electrons are paired. Therefore, VBT predicts that O2OX2 should be diamagnetic.
Now let’s examine how the electrons are arranged according to MOT. In MOT, unlike VBT, it involves the creation of bonding and anti-bonding Mos. MOs are basically the assumption of the wavefunctions of atomic orbitals. In O2OX2 the 2s AOs of each oxygen atom are constructively and destructively overlapping with each other while 2p AOs also constructively and destructively are overlapping with each other The resulting MOs for O2OX2 looks like this:
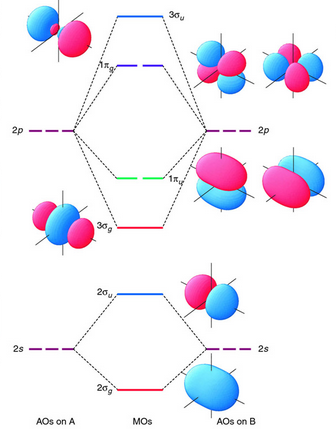
Fig 5: Molecular objects bonding and overlapping.
Now that we have the MOs, all we got to do is fill them with electrons using the same method that we use for AOs. In doing so we get:

Fig 6: Note that we have 2 unpaired electrons. Therefore, MOT correctly predicts that O2OX2 should be paramagnetic, unlike VBT which predicts that O2OX2 is diamagnetic.
Molecular Orbital Theory
Molecular Orbital Theory was initially used to explain the bonding in molecules that could not be explained by Valence Bond Theory. These are the molecules that generally involve some attribute resonance. Resonance implies that a bond is neither single nor double but some hybrid of the two. Valence bond theory only describes the bonding of single or double or triple bonds. It does not provide an explanation for resonance bonding.
Molecular orbital theory does describe resonance.
The Rules of Molecular Orbital Theory:
First principle: The number of molecular orbitals produced will be always equal to number of atomic orbitals brought by the atoms that have combined.
Second principle: Bonding molecular orbitals are lower in energy that the parent orbitals, and the antibonding orbitals are higher in energy.
Third principle: Electrons of the molecule are placed at orbitals from lowest to successively higher energy
Fourth principle: Atomic orbitals join together to form molecular orbitals most effectively when the atomic orbitals are of the same energy.
Principle 1: Example - Hydrogen (H2) Each hydrogen atom has a single valence bond orbital, this being the 1s orbital. Two molecular orbitals
can be formed by the constructing and destructing overlap of these two atomic orbitals. if we have two 1s atomic orbitals only two molecular orbitals are formed from them. This is the First Principle.

Fig 7: According to MO Theory, the two molecular orbitals that are formed are called s (sigma = bonding) and s* (sigma star = antibonding). In the case of H2 both of the valence electrons that form the bond between the hydrogens fill the bonding or s orbital.
Principle 2 & 3: This interaction of atomic orbitals, which gives rise to the molecular orbitals, can also be shown in the form of an orbital (electron) energy diagram which shows the relative energies of the orbitals. In the given specific case of hydrogen each of the isolated atoms has one electron in its 1s orbital and when the atoms combine to form H2 the two electrons may be joined (with opposite spins) in the bonding molecular orbital, as shown below. The second principle explains why electrons will want to occupy molecular orbitals in the first place. As stability comes from lowering energy needs. Anyway...because the bonding molecular orbitals provide a lower energy, a more stable state is found for the electrons, they fill these orbitals first. This could explain the third principle statement also.
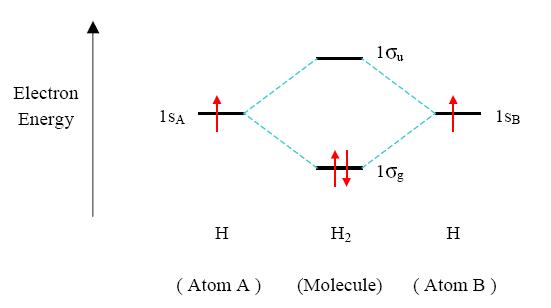
Principle 4: In H2 two 1s orbitals were combined were to form a single lower energy s molecular orbital. The fourth principle states that stability of molecular orbitals are easier to form when built out of atomic orbitals of same energies. This means that 1s orbitals should join with 1s orbitals and 2p orbitals should combine with 2p orbitals etc. to form the most stable molecular orbitals.
We Start with:

We then form Molecular Orbitals:
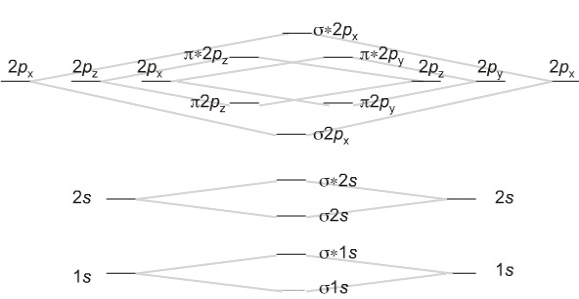
Which fill from lowest to highest energy as follows:
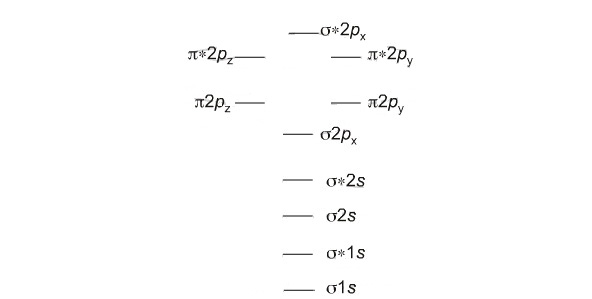
Bond Order
The bond order for a molecule can be calculated in the following manner: bond order = ½ (bonding electrons − antibonding electrons). since, the H2 molecule has a bond order of ½ (2 − 0) = 1. In the other case there is a single bond connecting the two H atoms in the H2 molecule. In the case of He2, on the other hand, the bond order is ½ (2 − 2) = 0. This means that He2 is not a stable molecule.
Let's try an example: N2
Each Nitrogen atom has 7 electrons and an electron configuration of 1s2 2s2 2p3. This results in a total of 14 electrons. How many molecular orbitals can be formed? Which molecular orbitals will be formed? Which orbitals may be filled first? What is the bond order for N2?
There are hundreds of diatomic molecules. This list includes diatomic elements and diatomic chemical compounds.
Mononuclear Diatomic Molecules
Some of these molecules consist of one element or are diatomic elements. Diatomic elements are examples of homonuclear molecules, where all of the atoms in the molecule are the same. The chemical bonds between the atoms are covalent and nonpolar. The seven diatomic elements are:
Hydrogen (H2)
Nitrogen (N2)
Oxygen (O2)
Fluorine (F2)
Chlorine (Cl2)
Iodine (I2)
Bromine (Br2)
5 or 7 Diatomic Elements
Some sources show that there are five diatomic elements, rather than seven. This is because only five elements can form stable diatomic molecules at standard temperature and pressure: the gases hydrogen, nitrogen, oxygen, fluorine, and chlorine. Bromine and iodine form homonuclear diatomic molecules at slightly higher temperatures. It's possible that an eighth element forms a diatomic molecule.
Heteronuclear Diatomic Molecules
Many diatomic molecules consist of two elements. In general, most elements form diatomic molecules, particularly when temperatures are high. However, when a certain temperature is past, all molecules break into their constituent atoms. However, the noble gases do not form diatomic molecules. Diatomic molecules consisting of two different elements are called heteronuclear molecules. Here are some heteronuclear diatomic molecules:
CO
NO
MgO
HCl
KBr
HF
SiO
Plots of energy level diagram of molecular orbitals
The first ten molecular orbitals may be arranged in order of energy as follows
σ(1s) <σ∗(1s) < σ(2s) <σ∗(2s) < π(2px) = π(2py) < σ(2pz) < π∗(2px) =π∗(2py) <π∗(2pz)
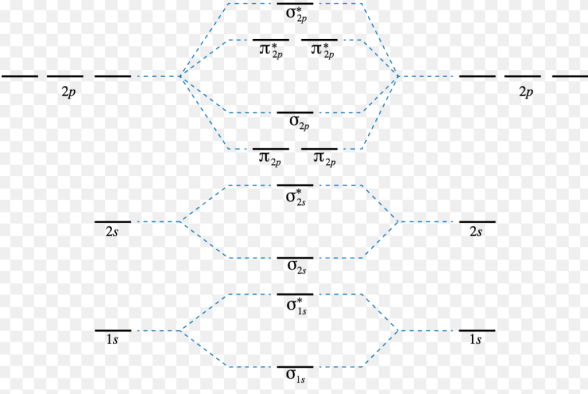
Fig. 8: Plots of energy levels.
In coordination chemistry the coordination number is the number of ligands attached to the central Ion (more specifically, the number of donor atoms). Coordination numbers are normally between two and nine. The number of bonds depends upon size, charge and electron configuration of the metal ion and the ligands.
Typically, the chemistry of complexes is dominated by interactions between s & p molecular orbitals of the ligands and the d orbitals of the metal ions. The s, p & d orbitals of the metal can accommodate 18 electrons. The maximum coordination number for a certain metal is thus related to the electronic configuration of the metal ion and the ratio of the size of ligands and the metal ion. Large metals and small ligands lead to high configuration numbers, (e.g., [MO(CN)8)4] small metals with large ligands lead to low coordination numbers (e.g., Pt[P(CMe3)]2). Due to the large size lanthanides, actinides and early transition metals have a high coordination number.
Geometrics
Different ligand structural arrangements result from coordination number. Most structures follow the pattern, central atom in the middle and the corners of that shape are the location of the ligands. These shapes are defined by orbital overlap between ligand and metal orbital and ligand-ligand repulsions, which tend to lead to certain regular geometrics. However, there are many cases that deviate from regular geometry. For example, ligands of different sizes and with different electronic effects often results in irregular bond lengths.
Isomerism in transitional metal compounds
Coordination isomerism is a form of structural isomerism in which the composition of the complex ions varies. In a coordination isomer the total ratio of ligand to metal remains the same, but the ligands attached to a specific metal ion change. Ionisation isomers can be thought of as occurring because of the formation of different ions and solutions. Ionisation isomers identical for a ligand has exchange places with an anion or neutral molecule that was originally outside the coordination complex.
In transition metals often form geometric isomers in which the same atoms are connected through the same types of bonds. But with the differences in their orientation in space. Coordination complexes with two different ligands in the cis and trans positions from a ligand of interest form isomers.
Crystal field theory
The Crystal field theory (CFT) is a model for the bonding interaction between transition metals and ligands. It describes the effect of attraction between the positive charge of the metal cation and negative charge on the non-bonding electrons of a ligand. When the ligand approaches the central metal ion the dangerously of electronic orbital states, usually d or f orbitals, are broken due to the statistic electric field by a surrounding charge distribution. CFT successfully accounts for some magnetic properties, colours, hydration energies of transition metal complexes, but it does not help to describe bonding
Energy level diagrams for transition metal ions and their magnetic properties
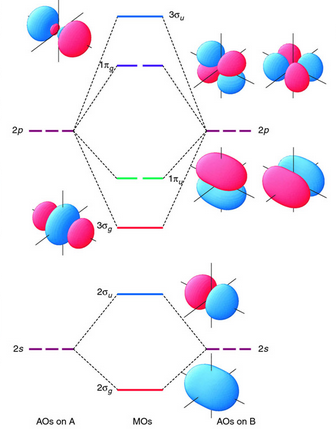
Fig.9 Energy level diagram for transition metal ions
Magnetic properties of transition metal ions
There are various substances which show magnetic behaviour. There are few substances that are attracted by the magnetic field and are called paramagnetic. This phenomenon is called Para magnetism. Paramagnetic property is only seen when the substance has one or more unpaired electrons. When a substance possesses a permanent magnetic moment, it is known as ferromagnetic and the phenomenon is called ferromagnetism. On analysis, we also have substances which are repelled by magnetic field and are called as diamagnetic substances. A substance shows diamagnetism when it has only paired electrons.
Most of the transition elements show paramagnetic behaviour. The unpaired electrons in (n-1) d orbitals are responsible for the magnetic properties. The paramagnetic character of the transition metals increases on moving from left to right as the number of unpaired electrons increases from one to five. The middle elements are found to possess the maximum paramagnetic property. The magnetic properties decrease with the decrease in the number of unpaired electrons. The transition metals which contain paired electrons depict diamagnetic behaviour.
References: