Module 3C
Partial Differential equation (First order)
Partial differential equation are those equation which contain partial differential coefficient, independent variables and dependent variables. The independent variable will be denoted by x and y and the dependent variable by z . The partial differential equation coefficient are denoted as follows.
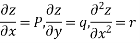
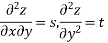
Orders
Order of a partial differential equation is the same as that of the order of the highest differential coefficient in it.
Method of forming partial differential equation
A partial differential equation is formed by two method
(i) By eliminating arbitrary constant
(ii) By eliminating arbitrary function.
Method of elimination of arbitrary constant
Example. Form a partial differential equation from
Ans. Given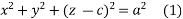 
Equation contains two arbitrary constant a and c.
Differentiating equation 1 partially with respect to x we get
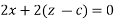
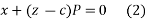
Differentiating equation 1 partially with respect to y we get
2y+2(z -c)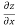
=0
y+(z -c) q=0 (3)
Eliminate c from (2) and (3) we get from (2) ( z -c)=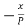
Putting the value of (z -c) in (3) we get
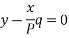
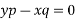
Method of elimination of arbitrary function
Example: Form the partial differential equation from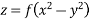 
Ans. Given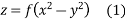 
Differentiating equation 1 with respect to X and y we get
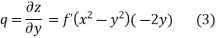
Dividing equation 2 by 3 we get
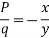
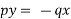
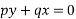
Solve the partial differential equation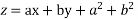 
Ans. Given that,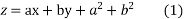 
Differentiating (1) partially with respect to x and y we get
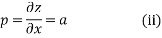
Noe eliminating a,b from these above equations we have
Which is required partial differential equation?
Que. Form a partial differential equation by eliminating a, b from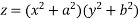 
Ans. Given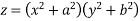 
(1)
Differentiating (1) partially with respect to x and y we get
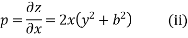
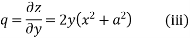
Differentiating (i) and (ii) we have
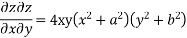
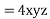
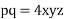
Lagrange's linear equation:-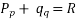 
Working rule:
Step1:- Write down the auxiliary equation
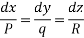
Step2:- Solve the above auxiliary equation
Let us two solution be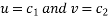 
Step3:- Then 
is the required solution of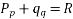 
Example:-
Solve 
Ans. AE are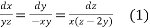 
From first two members of the equation
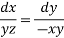
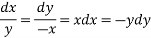
On integrating
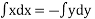
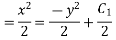
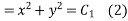
From last two members of the equation
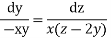
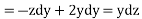
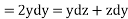
On integrating
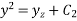
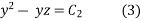
From (2) and (3)
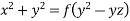
Method of multipliers
Let the AE be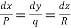 
l, m, n may be constant or function of x y z then we have
l, m, n are chosen in such a way that l p +m q + n R=0
Thus,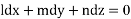 
Solve this differential equation if the solution is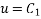 
Similarly choose another set of multipliers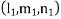 
and if the second solution is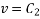 
Required solution is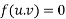 
Solve 
Ans.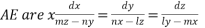 
Using multipliers xyz we get
Each fraction=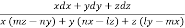
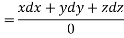
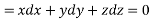
On integrating
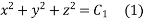
Again using l,m,n of multipliers
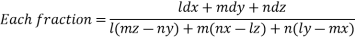
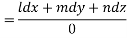
On integrating
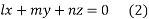
From (1) and (2) we get
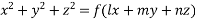
Partial differential equations Non linear in P and q
Type I
Equation of the type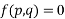 
Example: Solve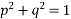 
Ans. Let z=ax+by+c (1)
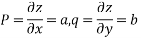
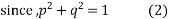
Putting p=a , q=b in equation 2
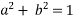
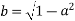
Putting the value of b in equation 1
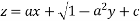
Type 2:- Equation of the type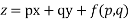 
its solution is z=ax +by + f(a ,b)
Solve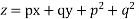 
Ans. Given,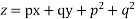 
Put p=a, q=b
Solution is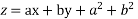 
Solve. y2 zp-x2 zq=x2 y
Ans. The given equation is of the Lagrange’s form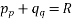 
Where,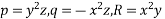 
The AE is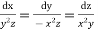 
From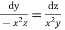 
On integrating,
Also,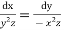 
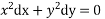
On integrating
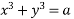
General solution is
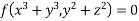
Solve.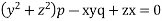 
Ans. AE is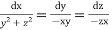 
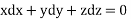
On integrating
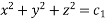
On integrating,
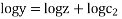
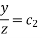
General solution is
Method of Multipliers
Solve. (a)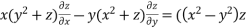 
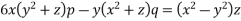
This is Lagrange’s equation
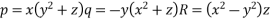
The subsidiary equation are
Using multipliers x, y, -1 we get
Each ratio =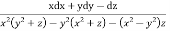 
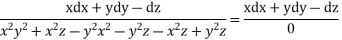
On integrating we get
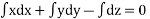
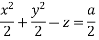
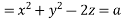
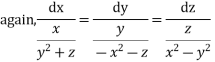
Each ratio =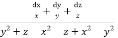 
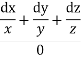
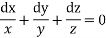
On integrating we get
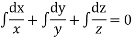
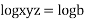
The general solutions are
Solve.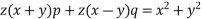 
Ans. Given,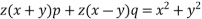 
The Lagrange’s subsidiary equation are
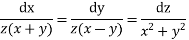
Choosing x, -y, -z as multipliers we get
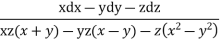
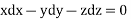
On integrating
is an arbitrary constant.
Again choosing, y, x, -z as multipliers
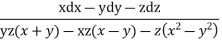
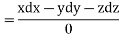
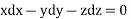
On integrating,
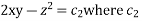is an arbitrary constant.
Hence required solution is
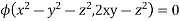
Partial Differential Equation non linear in p and q
Type A
Solve. 
Ans. Here 
The solution to given equation is
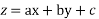
Where,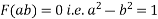 
Hence b can be expressed in terms of a as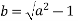 
Thus complete solution is
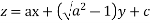
Solve.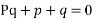 
Ans. Here, F(pq)=pq+p+q
A complete solution of a given equation is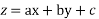 
Since,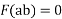 
i.e.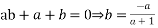 
The solution is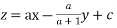 
Type 2
Solve.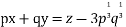 
Ans. The given equation can be written as 
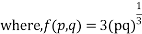
Complete solution is
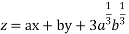
Solve. 
Ans. The given equation is of the form
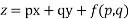
Its solution is given by
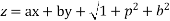
TEXTBOOKS/REFERENCES:
- S. J. FARLOW, PARTIAL DIFFERENTIAL EQUATIONS FOR SCIENTISTS AND ENGINEERS, DOVER PUBLICATIONS, 1993.
- R. HABERMAN, ELEMENTARY APPLIED PARTIAL DIFFERENTIAL EQUATIONS WITH FOURIER SERIES AND BOUNDARY VALUE PROBLEM, 4TH ED., PRENTICE HALL, 1998.
- IAN SNEDDON, ELEMENTS OF PARTIAL DIFFERENTIAL EQUATIONS, MCGRAW HILL, 1964.
- MANISH GOYAL AND N.P. BALI, TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS, UNIVERSITY SCIENCE PRESS, SECOND EDITION, 2010.
