Module 3D
Partial Differential Equation- Higher Order
Rule for finding the CF
Let f(D,D’)z=F(x)
Consider the equation 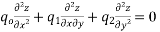
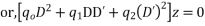
Step I: Put D=m and D’=1
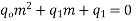
This is the auxiliary equation .
Step 2 : Solve the AE
Case I- If the roots of AE are real and different say 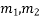
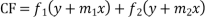
Case 2 :If roots are equal say m
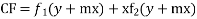
Solve: 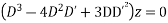
Ans. 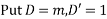
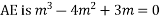
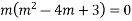

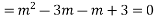
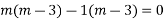
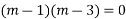
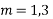
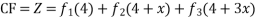
Solve : 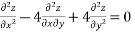
Or
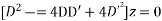
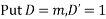
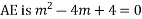
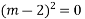
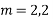
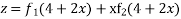
Solve. 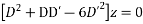
Ans. Given 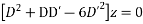
Its AE is 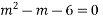

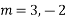
Complete solution is
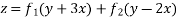
Solve. 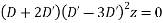
Ans. Its AE, put D = m, D’ = 1
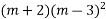
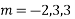
Complete solution is
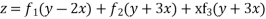
Rules for finding the PI
Given f(D D’)z=F(x y)
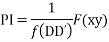
Case I : When 
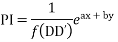
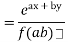
Put D=a and D’=b
Solve 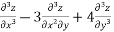
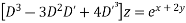
Ans. 
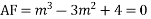
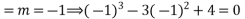
(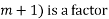
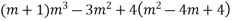
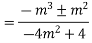

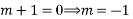

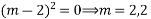
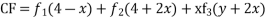
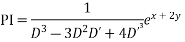
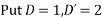
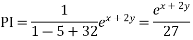
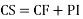
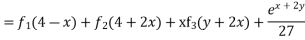

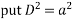
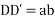

Solve. 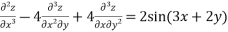
Ans. Given 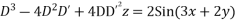
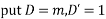
AE is 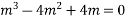
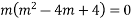
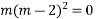
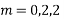
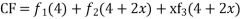
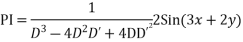
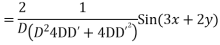
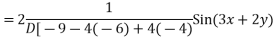
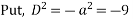
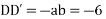
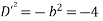
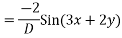
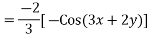
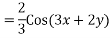
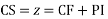
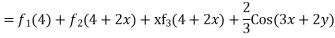
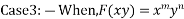
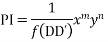

Expand 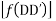 in ascending power of D or D’ and operate on
in ascending power of D or D’ and operate on 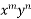 term by term.
term by term.
Solve. 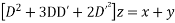
Ans. Put, 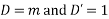
AE is 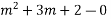
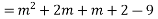
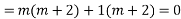
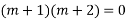
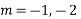
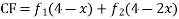
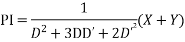
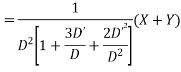
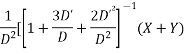
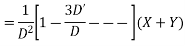
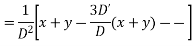
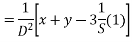
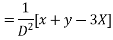
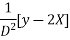
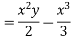
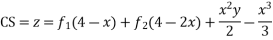
Solve. 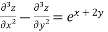
Ans. Given equation in symbolic form

Its AE is 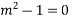
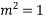
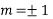
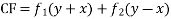
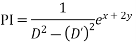
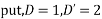
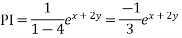
Complete solution is

Solve. 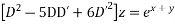
Ans. Its auxiliary equation is
Put, D = m, D’ = 1
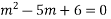
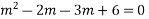
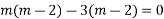
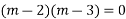
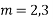

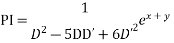
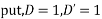
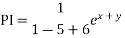
Complete solution is

Solve. 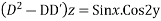
Ans. Put D = m, D’ = 1
The AE is 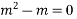
m2-m=0
m=0,1

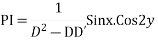
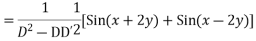
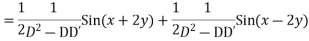
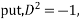
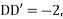 in the first integral and
in the first integral and 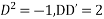 in the second integral
in the second integral
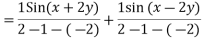

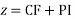
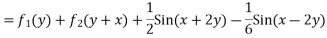
Solve. [D2-6DD'+9D'2]z=(6x+2y)+tan(3x+y)+e3x+2y
For complementary function
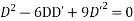
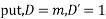
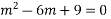
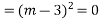
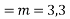
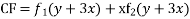
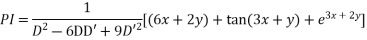
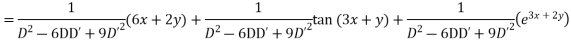
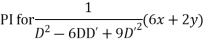
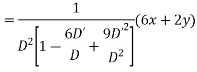

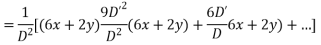
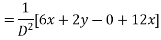
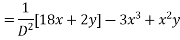
PI for 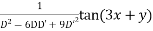
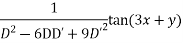
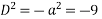
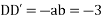
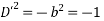

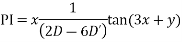
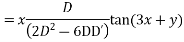
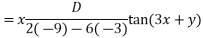
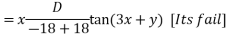
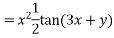
PI for 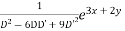
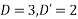
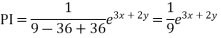
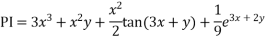
Complete solution CF + PI
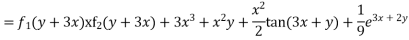
Solve 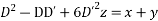
Ans. Put, D = m, D’ = 1
AE is 

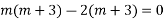
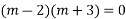
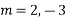

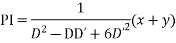
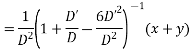
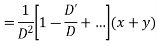
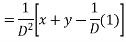

The complete solution is
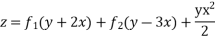
Solve. 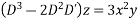
Ans. Put D = m, D’ = 1
Auxiliary equation is
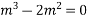
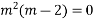
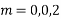

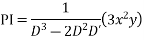
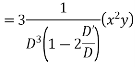
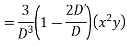
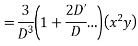
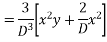
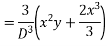

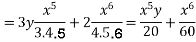
Complete solution is
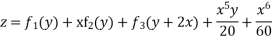

Flows :- Flow formulizes the idea of the motion of particle in a fluid.
Vibration :- Vibration are oscillation in mechanical dynamic system.
Diffusion:- The diffusion equation is a parabolic particle differential equation.
Charpits Method
f(xyz . P q)=0
Dz=Pdx + qdy
Subsidiary equation are
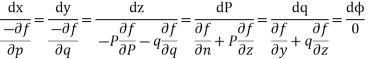
Solve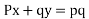
Ans. 
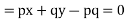


Charpits Equation are
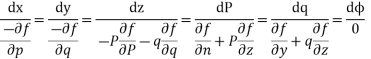
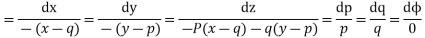
Taking two members
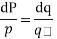
On integrating
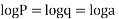
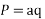

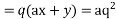
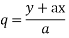
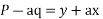
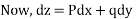
Putting for p and q we get
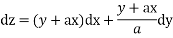
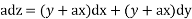
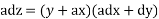
On integrating
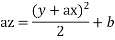
Solve. 
Ans. Let,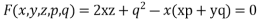
Then charpits Equation are

From first and last equation we get
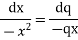
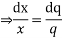
On integrating
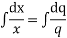
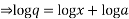
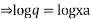
⇒q=xa
Then the equation 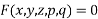
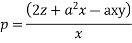
So that the relation 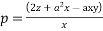 leads to
leads to 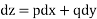

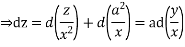
On integration
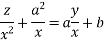
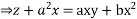
Which is a complete y integral
Solve. 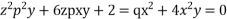
Ans. 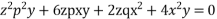
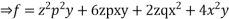
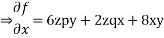
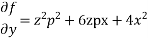
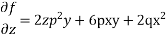
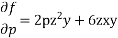
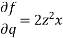
Charpits auxiliary equations are
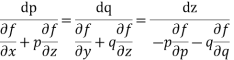
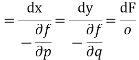
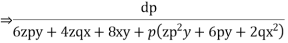
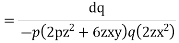
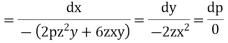
From the first and last members we get
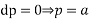
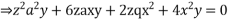
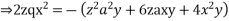
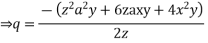
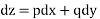
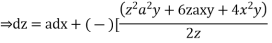
On integrating
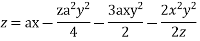
Initial value problem is 4(a)=P y’(a)=q
Boundary value problem is 4(a)=Py(b)=q
Solve. Given,  if u (x, 0) =0, u (0, t) = t
if u (x, 0) =0, u (0, t) = t
Ans. LET, u (x, s) = L [u (x, t)(s) for the Laplace transform of u
Then applying the Laplace transform to this equation
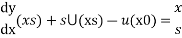
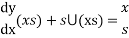
This is a constant coefficient first order differential equation
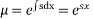
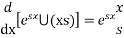
Integrating both sides we get
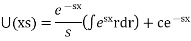


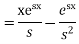
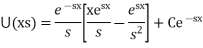
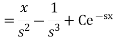
Using boundary conditions
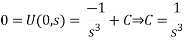
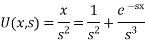
Taking the inverse Laplace transform we have
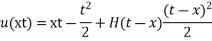
Solve. Given, 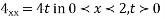
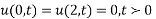
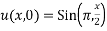

Ans. 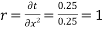
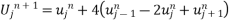
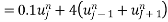
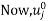
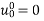 using boundary and initial condition
using boundary and initial condition
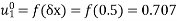
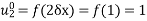
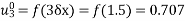
Now, 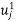 such that
such that 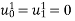
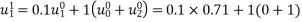

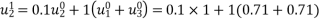
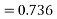
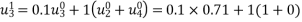
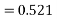
Solve. Given, 
Let, 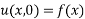
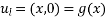
Ans.  where
where 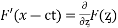
Also, 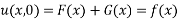
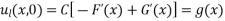
After differentiation of above equation with respect to x we get
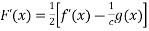
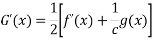
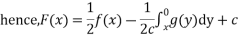
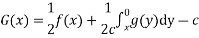
Where C is integration constant
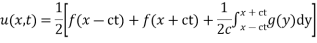
Using implicit method
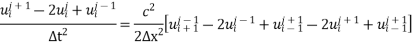
Let, 
For equation g (k)
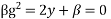
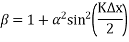
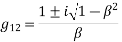
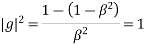
This is implicit scheme.
3.5  Alembert’s solution of Wave Equation
Alembert’s solution of Wave Equation
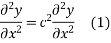
Let us introduce that two independent variables =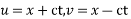
So that y becomes a function of u and v

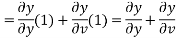
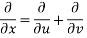
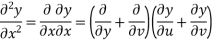

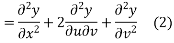
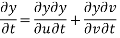
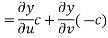
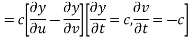
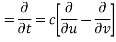
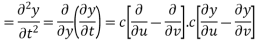
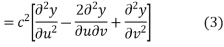
Putting the value of
From (2) ,(3) and (1) we get
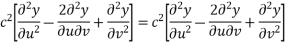
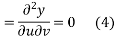
Integrating (4) with respect to v we get
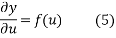
Where 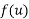 is constant in respect to v
is constant in respect to v
Again integrating equation (5)
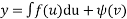
Where 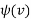 is constant in respect to u.
is constant in respect to u.
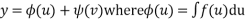
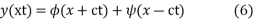
Duhamel’s principle is solution to this problem is
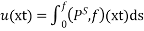
Where 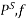 is the solution of the problem
is the solution of the problem
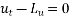
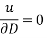
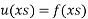
Example. 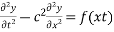
Where,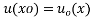
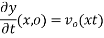
Using the method of separation of variable
Solve. 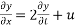 where
where 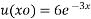
Ans.  (1)
(1)
Let, u=X(x)T(t) (2)
Using (2) in (1) we get

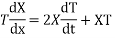
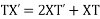
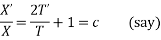
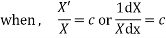
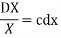
On integrating
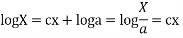
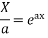
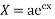
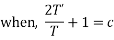
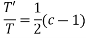
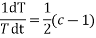
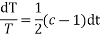
On integrating 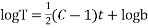
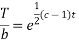

Putting the value of X and T in (2) we get

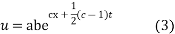

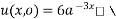
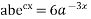
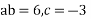
Putting the value of a, b, and c we get
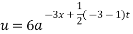
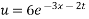
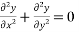
Laplace equation in polar co-ordinates
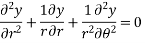
Laplace equation in spherical co-ordinates

Method of separation of variables
The equation for variation of the string is 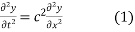
The solution of equation (1) is
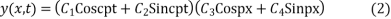
Let l be the length of the string
Equation of OB is
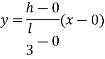
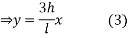
Equation of BC is
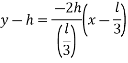

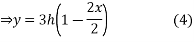
Equation of CA is
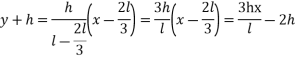

Hence the boundary conditions are
y (0, t) = 0
y (l, t) = 0
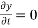 when t = 0
when t = 0
And, y (x, 0) = 
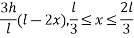
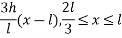
From (2)
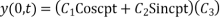
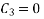
From (2)
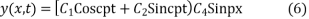
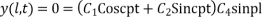
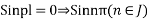
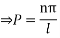
From (6)

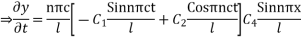
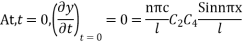
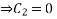
From (7)
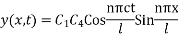
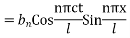
The most general solution is
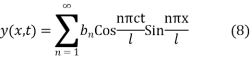
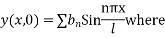
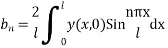
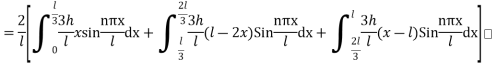
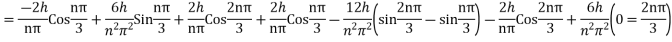
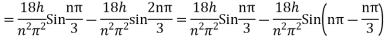

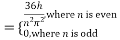
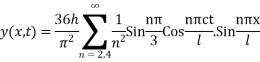
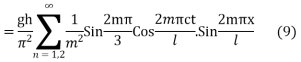
Where n = 2m
Which is required expression for y (x, t)
Putting, 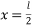 in equation (6) we get
in equation (6) we get
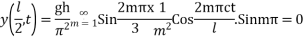
Hence mid point of string is always at rest.
Solve. 
Ans. Given, 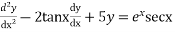
Multiply both sides of the equation by cos x
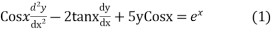
Let, u (x) = y (x) Cos x (2)
Find 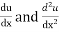
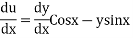
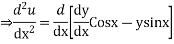
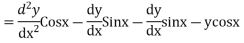

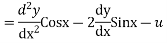
Thus from last equality we get
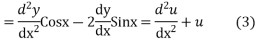
Substitution of the (3) in (1) we get
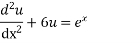
For complementary solution
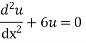
Put, 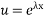

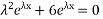
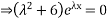
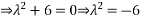
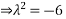


The obtained roots give
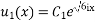

The general solution is the sum of 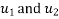
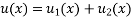
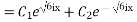
Apply Euler’s identity
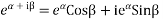
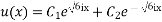
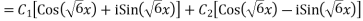

Redefine 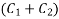 as
as 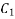 and
and  as
as 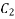
Since these are arbitrary constant

Determine the particular solution to 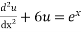 by method of undetermined coefficients
by method of undetermined coefficients
The particular solution to 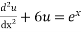 is of the form
is of the form
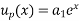
Substitute the particular solution 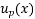 into the differential equation
into the differential equation
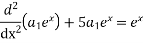
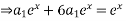
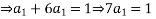
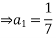
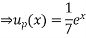
The general solution is
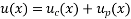
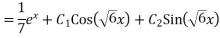
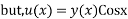
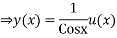
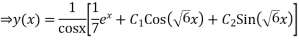
TEXTBOOKS/REFERENCES:
- S. J. FARLOW, PARTIAL DIFFERENTIAL EQUATIONS FOR SCIENTISTS AND ENGINEERS, DOVER PUBLICATIONS, 1993.
- R. HABERMAN, ELEMENTARY APPLIED PARTIAL DIFFERENTIAL EQUATIONS WITH FOURIER SERIES AND BOUNDARY VALUE PROBLEM, 4TH ED., PRENTICE HALL, 1998.
- IAN SNEDDON, ELEMENTS OF PARTIAL DIFFERENTIAL EQUATIONS, MCGRAW HILL, 1964.
- MANISH GOYAL AND N.P. BALI, TRANSFORMS AND PARTIAL DIFFERENTIAL EQUATIONS, UNIVERSITY SCIENCE PRESS, SECOND EDITION, 2010.