Module 4A
Complex Variables: Differentiation
Let f(x) be a small valued function of the variable 
then
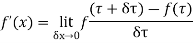
Provided that the limit exists and is independent of the path along which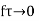 
Example. If 
.
Solution.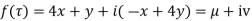 
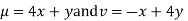
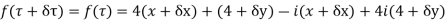
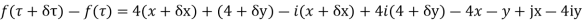
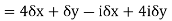
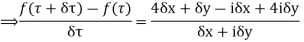
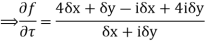
Along real axis,
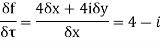
Along imaginary axis
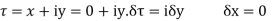
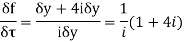
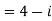
(1) Prove that f(z)=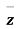
has no derivative
Sol We have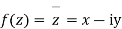 
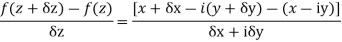
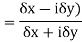
Now if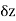 
is real then 
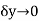and we have
If we let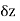 
approach to zero along y=mx so 
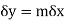then
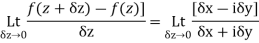
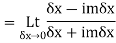
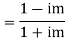
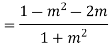
Which implies that there are infinitely many values of the above limit depending upon the choice of m? Thus it is clear that 
has no derivative at the origin
(2) Test the differentiability of the function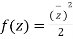 
for 
and f(0)=0
Solution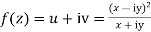 
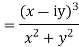
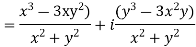
Since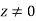 
and f(0)=0
Thus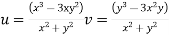 
For testing the differentiability of f(z) at z=0 let us first take z approaching 0 along the x axis then
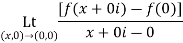
But if we let z approach 0 along the line y=x then
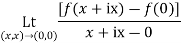
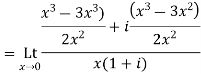
=-1
The two limit are not equal we conclude f(z) is not differentiable at the origin.
If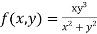 
where (x,y)=(0,0)
3. Prove that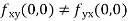 
Answer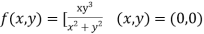 
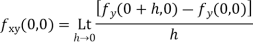
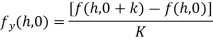
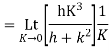
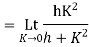
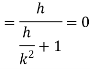
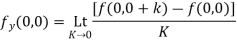
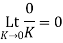
Again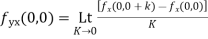 
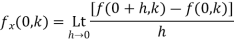
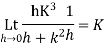
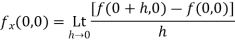
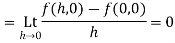
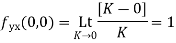
Theorem; The necessary condition for a function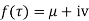 
to be analytic at all the points in a region R are
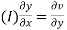(ii)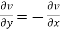 
Provided,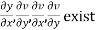 
Proof;\
Let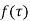 
be an analytic function in region R.
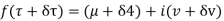
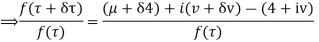
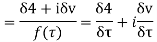
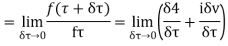
Along real axis
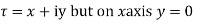
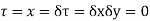
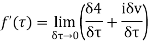
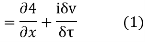
Along imaginary axis
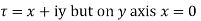
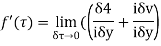
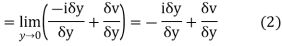
From equation (2) and (3)
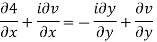
Equating real and imaginary parts
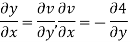
This is called Cauchy Riemann Equation
A function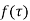 
is said to be analytic at a point 
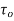if f is differentiable not only at 
but an every point of some neighborhood at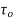 
.
Example, Prove that the function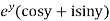 
is an analytical function.
Solution. Let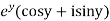 
=u+iv
Let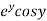 
=u and 
=v
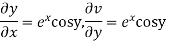
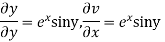
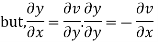
Hence e-R-Equation satisfied.
Prove that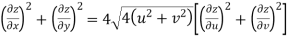 
Answer Given that
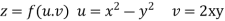
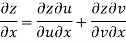
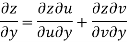
Since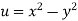 
V=2xy
Now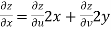 
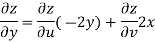
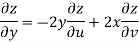
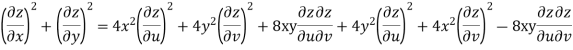
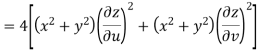
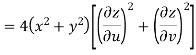
But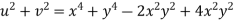 
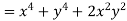
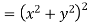
Hence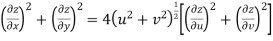 
State and prove sufficient condition for analytic functions
Answer Statement – The sufficient condition for a function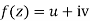 
to be analytic at all points in a region R are
1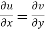 
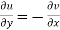
2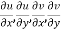 
are continuous function of x and y in region R.
Proof :- Let f(z) be a simple valued function having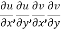 
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
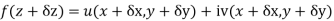
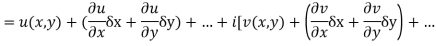
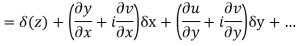
Ignoring the terms of second power and higher power
We know C-R equation
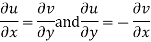
Replacing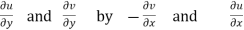 
Respectively in (1) we get
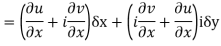
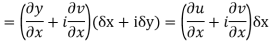
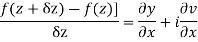
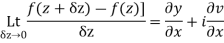
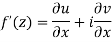
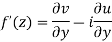
Show that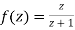 
is analytic at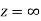 
Ans The function f(z) is analytic at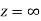 
if the function 
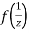is analytic at z=0
Since 
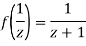
Now 
is differentiable at z=0 and at all points in its neighbourhood Hence the function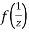 
is analytic at z=0 and in turn f(z) is analytic at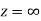 
Any function which satisfies the Laplace equation is known as harmonic function.
i.e.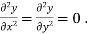 
Example; Prove that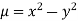 
is Harmonic Function.
Solution.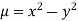 
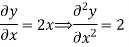
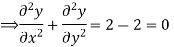
Hence function is harmonic.
Prove that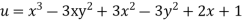 
is harmonic function
Ans Given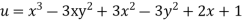 
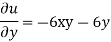
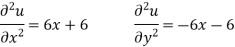
Thus 
Which shows that u is satisfies Laplace equation
Prove that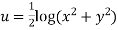 
is harmonic function
Ans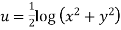 
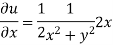
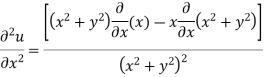
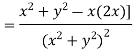
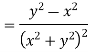
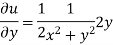
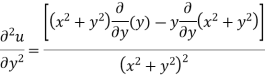
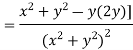
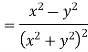
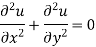
Which satisfies the Laplace equation. Hence the given function is harmonic
If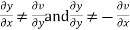 
Then function is harmonic conjugate.
A function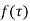 
is analytic in a domain if it is analytical at every point of the domain.
Position on exponential Trigonometric logarithm
Example; Prove that function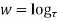 
is analytic function.
Solution. Real and Imaginary parts of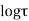 
are
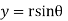
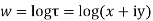
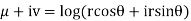
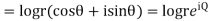
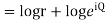
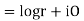
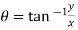
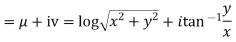
If,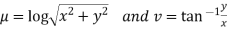 
On differentiating u,v we get
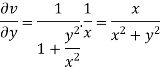
Again differentiating
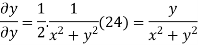
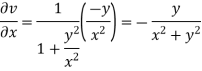
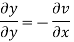
Hence e-R-Equation satisfies.
Properties
(i) Polynomials rational function are entire.
(ii) A differentiable function is always continuous but converse is not true.
Ques Determine P such that the function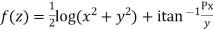 
analytic
Ans 
Hence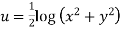 
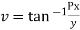
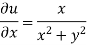
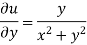
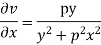
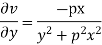
f(z) is analytic Cauchy Riemann should be satisfied that is
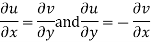
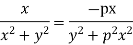
And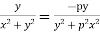 
P=-1
Question If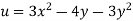 
and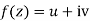 
is an analytic function of z=x+iy find f(z) in terms of z by Milne Thomas method
Answer f(z) is analytic since f is analytic
Let f’=u+iv
Then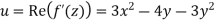 
Since u.v satisfy C-R conditions
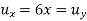
Integrating w.r.t y we get
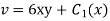
Differentiation v w.r.t x and using second C-R condition we get
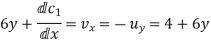
Thus V(x,y)=6xy+4x+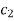
Where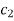 
is an arbitrary constant Then 
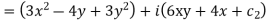
Applying Milne Thomas method replace x by z and y by 0 we get
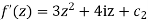
Integrating w.r.t z we get
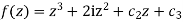
Where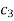 
is an arbitrary constant since f(1+ i)=0
We get
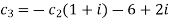
Thus 
If the sense of the relation as well as magnitude of the angle is preserved the transformation is said to be conformal.
Example; Find the conformal transformation of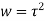 
.
Answer. Let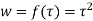 
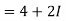
Theorem If W=f(z) represents a conformal transformation of a domain D in the z-plane into a domain D of the W plane then f(z) is an analytic function of z in D.
Proof We have u+iv=u(x,y)+iv(x,y)
So that u=u(x,y) and v=v(x,y)
Let ds and 
denote elementary arc length in the z-plane and w-plane respectively Then
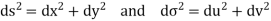
Now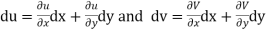 
Hence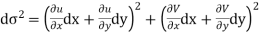 
Or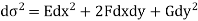 
Where 
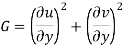
Now 
is independent of direction if
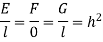
Where h depends on x and y only and is not zero. Thus the conditions for an isogonal transformation
And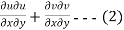 
The equation are satisfied if we get
Then substituting these values in 2 we get
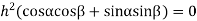
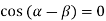
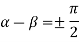
Taking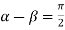 
i.e.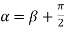 
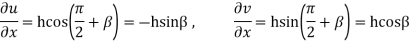
Also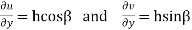 
Hence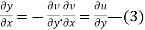 
Similarly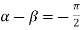 
i.e.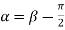 
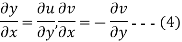
The equation (4) are the well known Cauchy -Reimann
Conformal mapping
Show that the mapping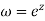 
is conformal in the whole of the z plane.
Ans Let z=x+iy
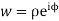
Then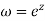 
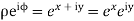
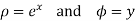
Consider the mapping of the straight line x=a in z plane the w plane which gives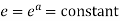 
which is a circle in the w plane in the anticlockwise direction similarly the straight line y=b is mapped into 
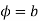which is a radius vector in the w plane.
The angle between the line x=a and y=b in the z plane is a right angle. The corresponding angle in the w plane between the circle e = constant and the radius vector 
is also a right angle which establishes that the mapping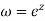 
is conformal.
Equation (1) is called bilinear transformation
If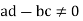 
then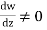 
i.e. transformation is conformal
From (1)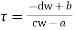 
This is called bilinear except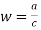 
Properties
(i) A bilinear transformation maps circles inti circles.
(ii) A bilinear transformation preserves cross ratio of four points.
Example, Find the fixed points and normal points of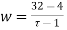 
Answer. The final points are b
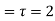
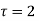is only fixed point
This transformation is parabolic.
Normal form
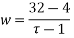
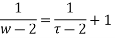
Every mobius transformation maps circles or straight line into circles or straight line
Proof : The equation of circle in the z plane may be written as
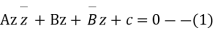
Where A, C are real and B is a complex constant such that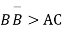 
If A=0 then (1) represents a straight line
Let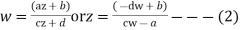 
Be any bilinear transformation. Then transform of (1) under (2) is
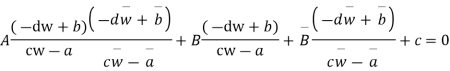
Or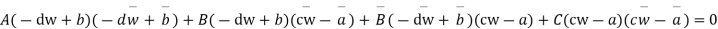 
Or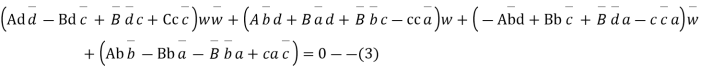 
Which is of the form
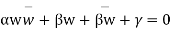
Where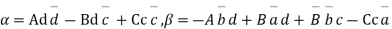 
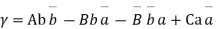
It is evident that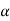 
of w and 
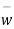are conjugate complex number
Further
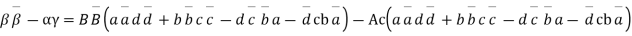
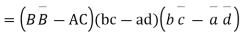
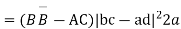
Theorem Every bilinear transformation with two finite fixed points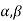 
can be part in the form
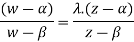
Proof Consider any bilinear transformation with 
as fixed points and suppose it transforms a point Y into the point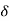 
. Then the points 
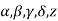are mapped into the points 
respectively since cross ratio is preserved under a bilinear transformed we have
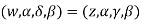
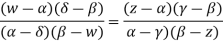
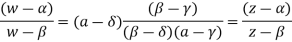
Which is of the form
TEXTBOOKS/REFERENCES:
- ERWIN KREYSZIG, ADVANCED ENGINEERING MATHEMATICS, 9TH EDITION, JOHN WILEY & SONS, 2006.
- J. W. BROWN AND R. V. CHURCHILL, COMPLEX VARIABLES AND APPLICATIONS, 7TH ED., MC- GRAW HILL, 2004.
- VEERARAJAN T., ENGINEERING MATHEMATICS FOR FIRST YEAR, TATA MCGRAW-HILL, NEW DELHI, 2008.
- N.P. BALI AND MANISH GOYAL, A TEXT BOOK OF ENGINEERING MATHEMATICS, LAXMI PUBLICATIONS, REPRINT, 2010.
- B.S. GREWAL, HIGHER ENGINEERING MATHEMATICS, KHANNA PUBLISHERS, 35TH EDITION, 2000.
