Module 4 B
Complex variable integration
Contour integration is the process of calculating the values of a contour integral around a given contour in the complex plane.
Solve 
where 
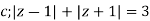
Answer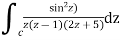 
Where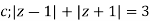 
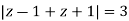
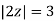
Poles of the inter are given by putting the denominator equal to zero.
Z(z-1)(2z+5)=0
Z=0,1,-5/2
The integrand has three simple poles at
Z=0,1,-5/2
The given circle |z|=3/2 with centre at z=0 and radius =3/2 encloses two poles z=0 and 1
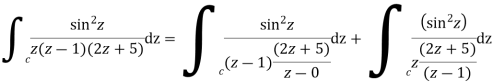
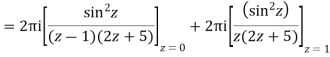
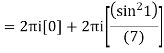
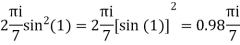
Solve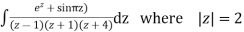 
Answer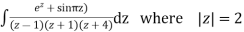 
Poles are
|z-0|=2
Poles 1 and -1 inside the circle
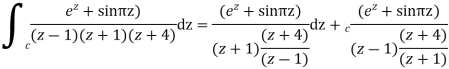
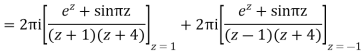
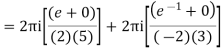
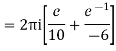
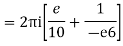
If a function f is analytic at all points interior to and on a simple closed contour c (i.e. f is analytic on some simply connected domain D containing c) then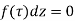 
for every closed contour c lying in D.
If f(
) is analytic within and on a closed curve c and if a is any point within c then f(a)=
Example. Use Cauchy integral formula to evaluate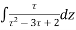 
Where 
is the circle |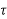
-2|=
Ans. Given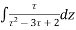 
The poles are determined by putting the denominator equal to zero
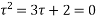
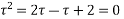
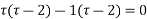
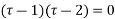
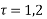
So these are the poles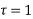 
and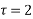 
There is only one pole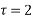 
inside the given circle
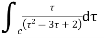
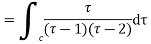
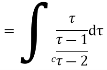
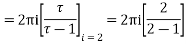
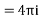
Liouville’s theorem states that a bounded holomorphic function on the entire Complex plane must be constant.
Maximum modulus Theorem
Let 
be analytic within and on a simple closed contour c. Then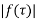 
reaches its maximum value on c (and not inside c) unless 
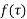is constant.
Let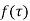 
be analytic at all points within a circle 
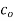with centre 
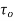and radius 
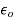. Then
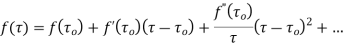
Expand the function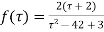 
In a Taylor's series about the point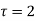 
Ans. Using partial fraction method
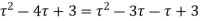
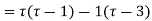
(τ-1)(τ-3)
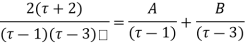
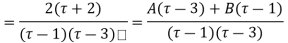
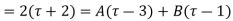
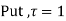
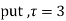
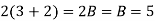
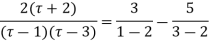
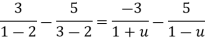
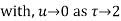
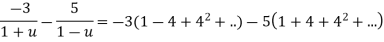
Both series converge when |4|<1
Therefore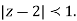 
The series converges in the circle centred at 
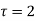with radius of 1.
Taylor’s series expansion is
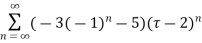
- Show that when 0<|z|<4
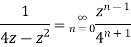
Solution When |z|<4 we have
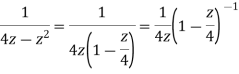
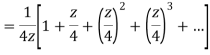
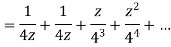
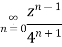
2. Expand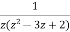 
for the regions
1) 0<|z|<1
2) 1<|z|<2
3) |z|>2
Solution Let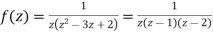 
Hence resolving into partial functions we get
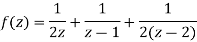
1) For 0<|z|<1 we have
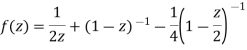
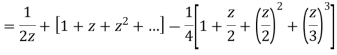
2) For 1<|z|<2 we have
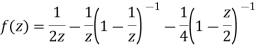
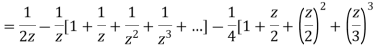
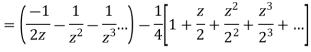
3) For |z|>2 we have
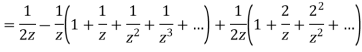
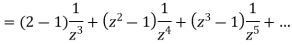
A point at which a function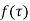 
is not analytic is known as a singular point or singularity of the function.
Example- Function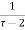 
has a singular point at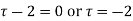 
Isolated singular point
The function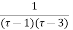 
has two isolated singular point namely 
Non isolated singularity
Function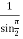 
is not analytic at the point where 
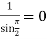i.e. at the points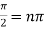 
Removal singular point
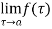exist and 
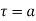a finite then is removable singular point
Essential singular point :-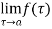 
does not exist then 
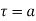is essential singular point.
1) Prove that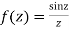 
has a removal singularity at z=0
Answer Given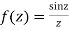 
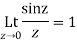
Exists and we can redefine f(z) as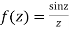 
when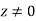 
and f(z)=1
When z=0
2) Find the type of singularity of the function 
at z=0
Answer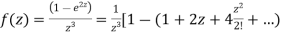 
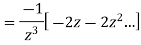
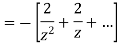
Therefore f(z) has a pole of order two at z=0
Let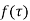 
be analytic in the ring shaped region D bounded by two concentric circles 
with centre 
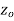and radii 
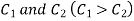and let be any point of D. Then
Example:- using Taylor's series
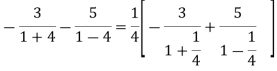
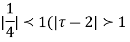
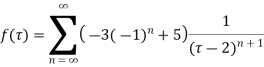
- Obtain the Taylor’s and Laurent’s series which represents the function
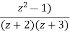in the regions
1) |z|<2
2) 2<|z|<3
3) |z|>3
Solution We have
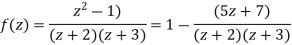
1) For |z|<2 we have
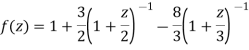
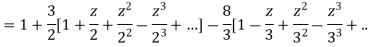
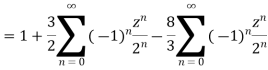
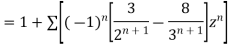
Which is Taylor’s series valid for |z|<2
2) For 2<|z|<3 we have
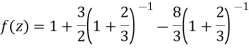
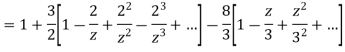
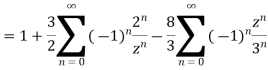
3) For |z|<3
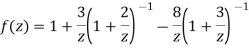
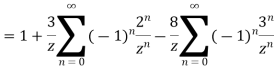
Let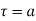 
be a pole of order m of a function 
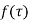and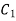 
circle of radius r with centre at 
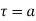which does not contain any other singularities except at 
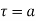then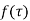 
is analytic within the 
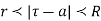can be expanded by Laurent’s series
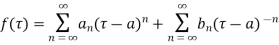
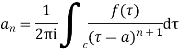
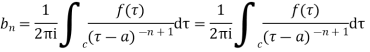
The coefficient of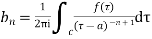 
is called residue of 
at the pole then 
Method of finding residue
(1) If 
has a simple pole at 
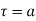then 
(2) If is of the form
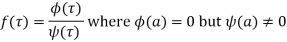
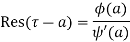
3) If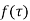 
has a pole of order n at 
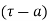then
5) Residue at a pole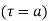 
of any order
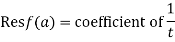
1) Residue of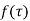 
at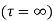 
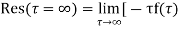
- Find residue of the function
Answer Let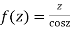 
The singularities of f(z) are given by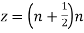 
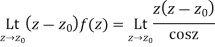
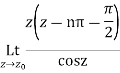
Which is of the form 
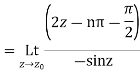
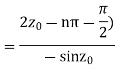
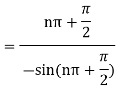
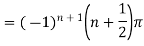
Find the residue of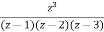 
at z=1
Answer Let f(z)=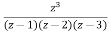
The poles of f(z) are determined by putting the denominator equal to zero
(z-1)(z-2)(z-3)=0
Z=1,2,3
Residue of f(z) at z=1=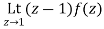
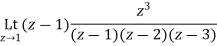
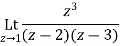
=1/2
2. Find the residue of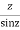 
Answer f(z)=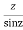
Poles are determined by putting sinz=0=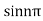
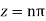
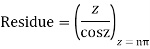
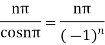
Hence the residue of the given function at pole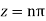 
is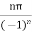 
If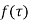 
is analytic in a closed curve c except at a finite number of poles within c then
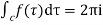[Sum of residue at the pole within c]
Evaluate the following integral using residue theorem
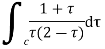
Where c is the circle.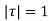
.
Ans. The poles of the integral are given by putting the denominator equal to zero
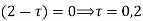
The integral is analytic on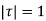 
and all points inside except
as a pole at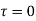 
is inside the circle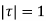 
Hence by residue theorem
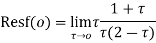
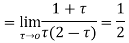
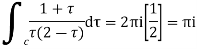
- Evaluate
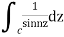where c;|z|=4
Answer Here f(z)=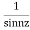
Poles are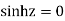 
Sin iz=0
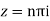
Poles 
Lie inside the circle |z|=4
The given function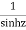 
is of the form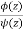 
Its pole at z=a is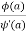 
Residue (at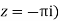 
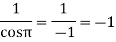
Residue at z=0=
Residue at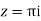 
=
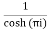
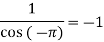
Residue at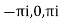 
are
Respectively -1,1 and -1
Hence the required integrand
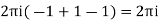
2. Evaluate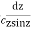 
:c is the unit circle about the origin
Answer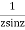 
=
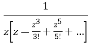
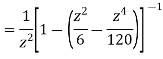
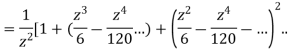
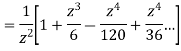
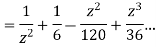
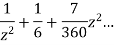
This shows that z=0 is a pole of order 2 for the function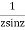 
and the residue of the poles is zero(coefficient of 1/z)
Now the pole at z=0 lies within c
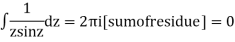
3. Evaluation of definite integrand
Show that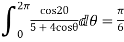 
Solution I=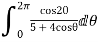 
Real part of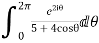 
Now I= 
=
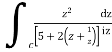
Putting z=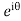
where c is the unit circle |z|=1
I=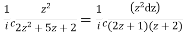
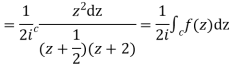
Now f(z) has simple poles at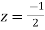 
and z=-2 of which only 
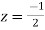lies inside c.
Residue at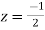 
is 
=
=
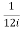
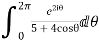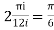
Now equating real parts on both sides we get
I=
4. Prove that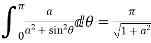 
Solution Let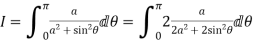 
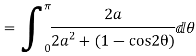
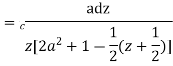
Putting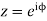 
where c is the unit circle |z|=1
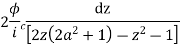
2ai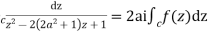
Poles of f(z) are given by the roots of
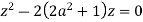
Or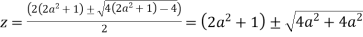 
Let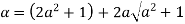 
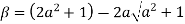
Clearly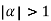 
and since 
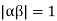we have 
Hence the only pole inside c is at z=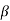
Residue (at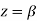 
)
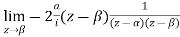
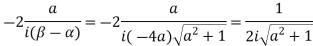
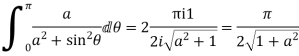
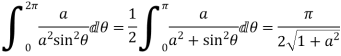
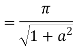
5. Evaluate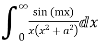 
Answer Consider 
Where c is the closed contour consisting of
1) Real axis from 
2) Large semicircle in the upper half plane given by |z|=R
3) The real axis -R to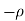 
and
4) Small semicircle given by |z|=
Now f(z) has simple poles at z=0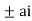 
of which only z=
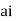is avoided by indentation
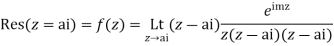
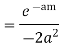
Hence by Cauchy’s Residue theorem
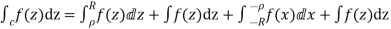
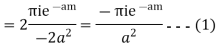
Since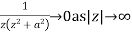 
and
Hence by Jordan’s Lemma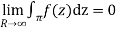 
Also since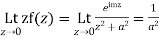 
Hence 
Hence as 
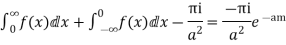
Equating imaginary parts we get
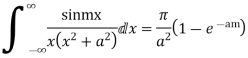
6. Prove that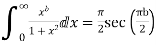 
Solution Consider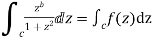 
Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure
Here we have avoided the branch point o, of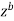 
by indenting the origin
Then only simple of f(z) within c is at z=i
The residue(at z=i) =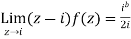
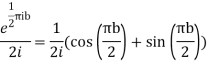
Hence by residue theorem
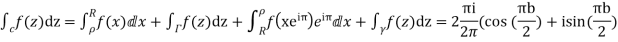
Since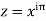 
on -ve real axis.
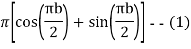
Now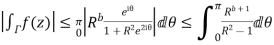 
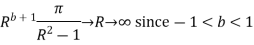
Similarly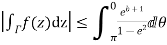 
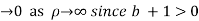
Hence when 
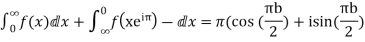
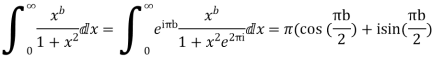
Equating real parts we get
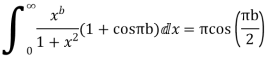
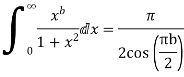
TEXTBOOKS/REFERENCES:
- Erwin Kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley & Sons, 2006.
- J. W. Brown And R. V. Churchill, Complex Variables And Applications, 7th Ed., Mc- Graw Hill, 2004.
- Veerarajan T., Engineering Mathematics For First Year, Tata Mcgraw-Hill, New Delhi, 2008.
- N.P. Bali And Manish Goyal, A Text Book Of Engineering Mathematics, Laxmi Publications, Reprint, 2010.
- B.S. Grewal, Higher Engineering Mathematics, Khanna Publishers, 35th Edition, 2000.
