Module 4C
Application of Complex integration by residues
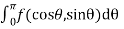
Where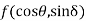 
is a rational function of 
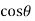and 
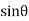
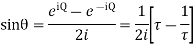
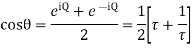
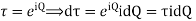
Evaluate.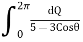 
Ans.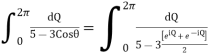 
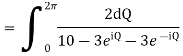
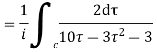
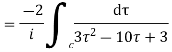
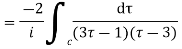
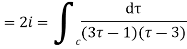
Role of the integral are given by
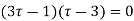
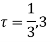
There is only one pole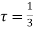 
inside the unit circle c
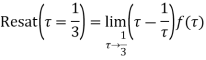
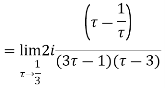
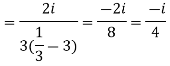
Hence by Cauchy Residue theorem
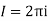[sum of the residue within contour]
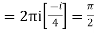
Evaluate. 
Ans. Given,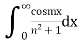
Consider the integral 
where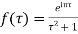 
taken round the close contour c consisting of the upper half of a large circle 
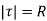and the real axis from –R to R.
Poles of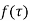 
are given by
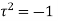
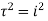
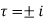
The only pole which lies within the contour is at 
The residue of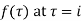 
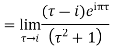
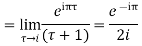
Hence by Cauchy Residue theorem
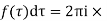Sum of residue
Equating the real part we get
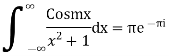
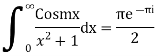
Evaluate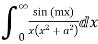 
Answer Consider 
Where c is the closed contour consisting of
1) Real axis from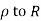 
2) Large semicircle in the upper half plane given by |z|=R
3) The real axis -R to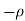 
and
4) Small semicircle given by |z|=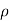
Now f(z) has simple poles at z=0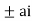 
of which only z=
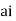is avoided by indentation
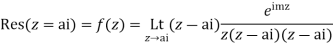
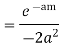
Hence by Cauchy’s Residue theorem
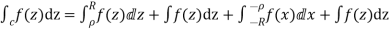
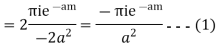
Since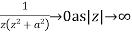 
and
Hence by Jordan’s Lemma 
Also since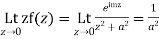 
Hence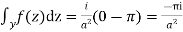 
Hence as 
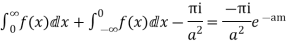
Equating imaginary parts we get
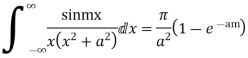
Prove that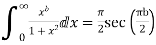 
Solution Consider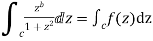 
Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure
Here we have avoided the branch point o, of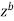 
by indenting the origin
Then only simple of f(z) within c is at z=i
The residue (at z=i) =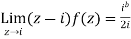
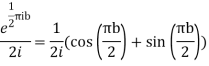
Hence by residue theorem
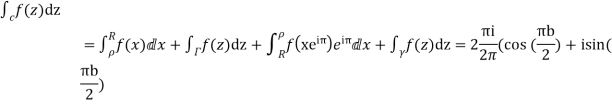
Since 
on -ve real axis.
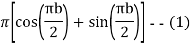
Now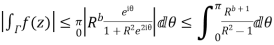 
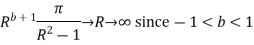
Similarly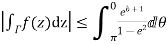 
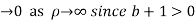
Hence when 
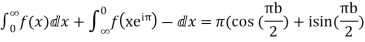
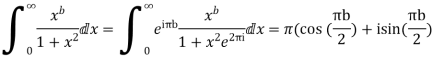
Equating real parts we get
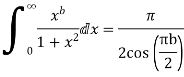
TEXTBOOKS/REFERENCES:
- Erwin Kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley & Sons, 2006.
- J. W. Brown And R. V. Churchill, Complex Variables And Applications, 7th Ed., Mc- Graw Hill, 2004.
- Veerarajan T., Engineering Mathematics For First Year, Tata Mcgraw-Hill, New Delhi, 2008.
- N.P. Bali And Manish Goyal, A Text Book Of Engineering Mathematics, Laxmi Publications, Reprint, 2010.
- B.S. Grewal, Higher Engineering Mathematics, Khanna Publishers, 35th Edition, 2000.
