MODULE 5A
NUMERICAL METHODS – 1
Finding root of a Polynomial Equation
f(x)= 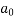
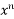 +
+ 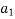
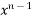 +
+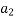
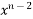 + ……+
+ ……+ 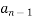 x +
x + 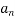 = 0 or a root of a transcendental Equation Which is combination of Polynomial Exponential function Trigonometric function etc. e.g
= 0 or a root of a transcendental Equation Which is combination of Polynomial Exponential function Trigonometric function etc. e.g 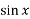 = x ,
= x , 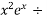 2 = 0 .
2 = 0 . 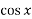 - x
- x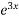 = 0 are all transcendental Equation.
= 0 are all transcendental Equation.
Bisection method 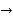 This method is based on the repeated application of the intermediate value theorem to obtain an approximation to the root of the Equation f(x) = 0. Suppose f(a) f(b)
This method is based on the repeated application of the intermediate value theorem to obtain an approximation to the root of the Equation f(x) = 0. Suppose f(a) f(b) 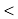 0 then a root lies between a and b . The mean value
0 then a root lies between a and b . The mean value 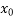 =
= 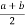 is taken as first approximate value of the root since f(a) and f(b) are of opposite sign . Let us consider the case f(a) is negative and f(b) is positive.
is taken as first approximate value of the root since f(a) and f(b) are of opposite sign . Let us consider the case f(a) is negative and f(b) is positive.
If f(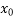 ) = 0 then obviously x =
) = 0 then obviously x = 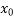 is a root of the Equation f(x) = 0 otherwise the root lies between
is a root of the Equation f(x) = 0 otherwise the root lies between 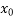
And b if f(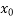 ) is negative and the root lies between a and
) is negative and the root lies between a and 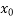 is positive.
is positive.
Find real root of the Equation 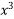 – 2x – 5 = 0 correct to three decimal places.
– 2x – 5 = 0 correct to three decimal places.
And here f(x )= 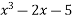
f(1) = 1-2-5 = -6
f(2) = 8-4 -5 = -1
f(3) = 27 – 6 – 5 = 1.6
Therefore at least one root lies between 2 and 3 and we take 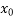 =
= 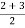 = 2.5
= 2.5
F(2.5) = 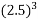 – 2(2.5) – 5 = 2.5 (6.25) – 10 = 15.625 – 10 = 5.625 = +ve
– 2(2.5) – 5 = 2.5 (6.25) – 10 = 15.625 – 10 = 5.625 = +ve
Hence root lies between 2 and 2.5.
The interval is now (2, 2.5) hence 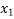 =
= 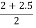 = 2.25
= 2.25
Now f(2.25) = 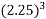 – 2(2.25) – 5
– 2(2.25) – 5
= 1.890625 = +ve
Root lies in 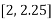 then
then 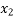 =
= 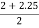 = 2.125
= 2.125
→ Newton- Raphson method → 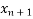 =
= 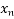 -
- 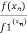 Where n = 0,1 , 2 -----
Where n = 0,1 , 2 -----
e.g using Newton Raphson method obtain the real root of the Equation x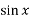 +
+ 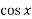 = 0
= 0
Ans → Let f(x) = x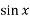 +
+ 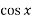
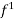 (x) = x
(x) = x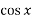
Let us take initial value of the root of f(x) = 0 as 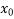 =
= 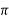
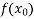 = 0 as
= 0 as 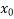 =
= 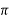
f(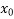 ) = -1
) = -1 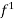 (
(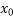 ) = -
) = -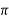 By N-R-M
By N-R-M
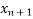 =
= 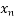 -
- 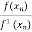 =
= 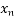 -
- 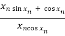 =
= 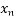 -
- 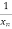 -
- 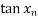
n = 0,1 ,2 , --------
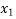 = 3.1416 -
= 3.1416 - 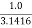 = 2.8233
= 2.8233
Similarly, 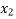 = 2.7986 &
= 2.7986 & 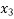 = 2.7984
= 2.7984
Repeating the process, we get 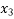 = 2.798
= 2.798
 Regula falsi method
Regula falsi method 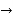 x =
x = 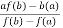
Find the approximate value of the root of the Equation 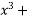 x – 1 = 0 near x = 1
x – 1 = 0 near x = 1
Using this method of falsi position two times
Ans 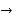 Given f(x) =
Given f(x) = 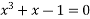
f(1)= 1 + 1 -1 = 1
f(0.5) = (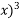 + (0.5) – 1 = - 0.375
+ (0.5) – 1 = - 0.375
The root lies between 0.5 and 0.1
Let 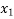 = 0.5
= 0.5 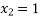
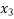 =
= 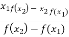 =
= 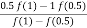
= 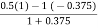 = 0.6363
= 0.6363
Now f(0.6363) = -0.1061
f(1) = 1
Root lies between 0.6363 and 1
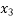 = 0.6363
= 0.6363 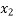 = 1
= 1
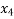 =
= 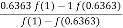 =
= 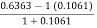 = 0.6712
= 0.6712
f(0.6712) = - 0.0264 f(1) = 1
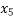 =
= 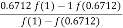
= 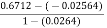
= 0.6797
Model question
(1) Solve the following Equation by N-R-M
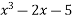
(2) Solve by bisection method up to three iteration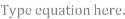
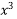 - 5x + 3 = 0
- 5x + 3 = 0
(3) Solve the equation by Regula falsi method
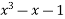 = 0
= 0
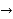 Finite difference
Finite difference 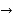 (i) Forward difference
(i) Forward difference
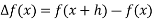
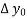 =
= 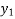 -
- 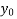
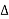
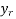 =
= 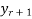 -
- 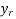 (r = 0, 1 , 2 ……)
(r = 0, 1 , 2 ……)
(ii) Backward difference
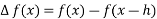
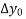 =
= 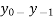
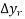 =
=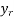
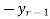 (r = 1.2.3 ……)
(r = 1.2.3 ……)
(iii) Central difference 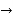
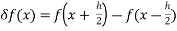
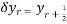 _
_ 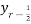 (r = 0,1,2 …..)
(r = 0,1,2 …..)
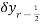 =
= 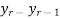 =
= 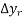
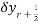 =
= 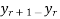 =
= 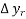
 Relation between operators
Relation between operators 
(1) Shift operator (E) 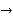 E f(x) = f(x+h)
E f(x) = f(x+h)
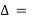 E – 1
E – 1
E = 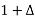
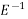 = 1 -
= 1 - 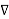
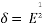 -
- 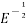
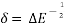 =
= 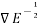
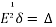
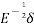 =
= 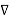
(2) Average 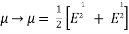
(3) Relation between 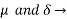
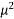 = 1 +
= 1 + 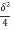
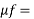
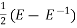
= 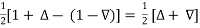
(4) Relation between E and D 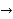
E = 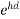
1 + 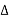 =
= 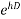
Newton Forward differences 
Y(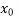 + rh) =
+ rh) = 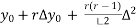
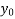 +
+ 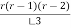
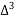
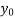 + ….
+ ….
Newton Backward difference 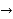
Y(x) = y (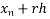 ) =
) = 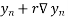 +
+ 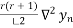 +
+ 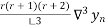 + …….
+ …….
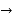 The population of a city in the decimal census is given in the following table
The population of a city in the decimal census is given in the following table
Year X | 1891 | 1901 | 1911 | 1921 | 1931 |
Population Y (in thousand) | 46 | 66 | 81 | 93 | 101 |
Approximate the population of the city in the years 1895 and 1925
Ans  Difference Table
Difference Table
X | Y | 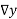 | 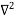 | 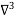 | 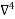 |
1891 | 46 | 20 |
|
|
|
1901 | 66 | 15 | -5 | -2 |
|
1911 | 81 | 12 | -3 | -1 | -3 |
1921 | 93 | 8 | -4 |
|
|
1931 | 101 |
|
|
|
|
Compute the population in 1895
Using Newton forward differences formula
Y(x) = 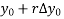 +
+ 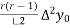 +
+ 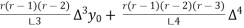
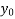 + …
+ …
Let 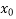 = 1891 h = 10 X =
= 1891 h = 10 X = 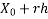 = 1895
= 1895
r = 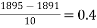
y(1895) = 46 + 0.4(20)+ 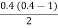 (-5)+
(-5)+ 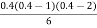 (2) +
(2) + 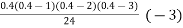
= 54.85 thousand (Approx)
Compute the population in 1925 using backward difference formula
Y(x) = 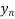 + r
+ r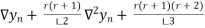
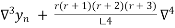
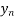 + ……..
+ ……..
Let 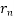 = 1931 r =
= 1931 r = 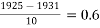
Y(1925) = 101 + (0.6) 8 + 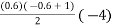 +
+ 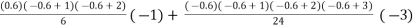
= 96.84 thousand only.
 Interpolation with unequal intervals
Interpolation with unequal intervals
Newton divided difference formula 
f(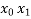 ) =
) = 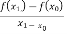
f(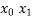
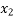 ) =
) = 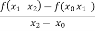
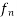 (x) = f(
(x) = f(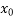 ) + (x -
) + (x - 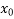 )f(
)f(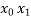 ) + (x -
) + (x -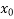 )(x -
)(x - 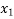 )f(
)f(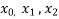 ) + ……
) + ……
e.g using divided difference interpolation
Find f(x)
x | 0 | 1 | 2 | 4 | 5 | 6 |
Y = f(x) | 1 | 14 | 15 | 5 | 6 | 19 |
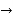 The divided difference table
The divided difference table
x | 4 | d.d of order1 | d.d of order2 | d.d of order3 | d.d of order4 | d.d of order5 |
0 | 1 |
|
|
|
|
|
1 | 14 | 13 | -6 | 1 |
|
|
2 | 15 | 1 | -2 | 1 | 0 |
|
3 | 5 | -5 | 2 | 1 | 0 | 0 |
4 | 6 | 1 | 6 |
|
|
|
5 |
| 13 |
|
|
|
|
6 | 19 |
|
|
|
|
|
Using formula
Y = f(x)= 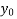 + (x -
+ (x - 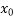 )
)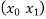 + (x -
+ (x - 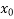 ) (x-
) (x- 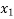 )f
)f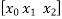 + (x -
+ (x - 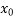 )(x -
)(x - 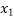 )(x -
)(x - 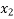 ) f
) f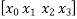 +…….
+…….
= 1 + (x - 0)(13) + (x - 0)(x-1)(-6)+ (x - 0)(x-1)(x -2)(1) + (x -0)(x-1)(x - 2)(x - 4)(0) + (x -0)(x - 1)(x -1) (x - 2)(x - 4)(x -5)0+ 0
= 1 + 13x + (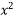 - x)(-6)+ (
- x)(-6)+ (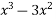 + 2x)(1) + 0
+ 2x)(1) + 0
= 1 + 21x - 9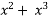
f(x) = 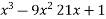
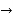 Using Lagranye’s interpolation Solve the following data
Using Lagranye’s interpolation Solve the following data
x | 300 | 304 | 305 | 307 |
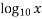 | 2.477 | 2.482 | 2.484 | 2.487 |
Calculate the approximate value of 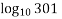
Ans. Using formula
y = 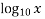 =
= 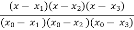
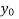 +
+ 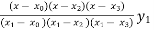 +
+ 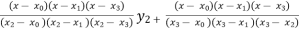
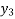
= 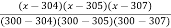 (2.477) +
(2.477) + 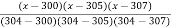 (2.482) +
(2.482) + 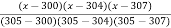 (2.484) +
(2.484) + 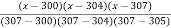 (2.4871)
(2.4871)
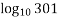 =
= 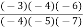 (2.477) +
(2.477) +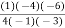 (2.4829) +
(2.4829) + 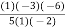 (2.4843) +
(2.4843) + 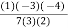 (2.4871)
(2.4871)
= 1.2739 + 4.9658 – 4.4717 + 0.7106
= 2.4786
Newton forward difference formula
Y = 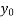 + P
+ P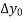 +
+ 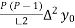 +
+ 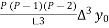 + ….
+ ….
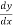 =
= 
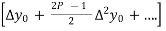
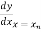 =
= 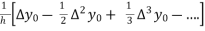

( 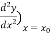 =
= 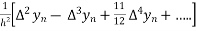
Where h = 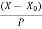
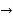 =
= 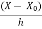
Backward difference 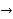
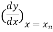 =
= 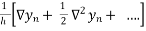
( 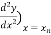 =
= 
(1) Find 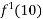 from the following table
from the following table
x | 3 | 5 | 11 | 27 | 34 |
f(x) | -13 | 23 | 899 | 17315 | 35606 |
x | 1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
4 | 2.71 | 3.32 | 4.05 | 4.95 | 6.04 | 7.3 | 9.05 |
(2)
Find 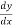 and
and 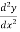 at x = 1.2 , x = 1.6 and x = 2.2
at x = 1.2 , x = 1.6 and x = 2.2
 Numerical integration
Numerical integration  f(x) by interoperating Polynomial
f(x) by interoperating Polynomial 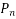 (x) and obtain
(x) and obtain
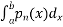
Which Will be taken as a approximate value of 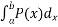 . This is also called quadrature.
. This is also called quadrature.
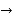 Trapezoidal rule
Trapezoidal rule 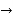
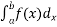 = h
= h 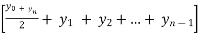 where h =
where h = 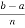
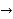 Simpson’s
Simpson’s 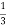 rule
rule 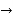
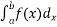 =
= 
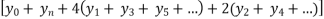
 Simpson’s
Simpson’s  rule
rule 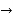
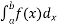 =
= 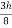
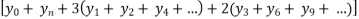
e.g Solve 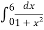 by (i) Trapezoidal rule , (ii) Simpson’s
by (i) Trapezoidal rule , (ii) Simpson’s  rule ,(iii) Simpson’s
rule ,(iii) Simpson’s  rule
rule
Ans 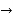 Let h = 1 or Let n = 6
Let h = 1 or Let n = 6
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
f(x) = 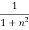 | 1 | 0.500 | 0.200 | 0.100 | 0.05 | 0.038 | 0.027 |
| 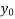 | 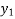 | 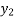 | 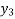 | 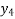 | 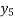 | 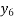 |
By Trapezoidal rule
I = 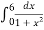 = h
= h 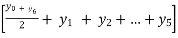
= 1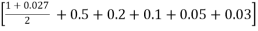
= 1.41
By Simpson’s rule
I = 
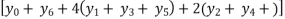
= 
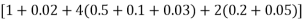
= 1.366
Simpson’s 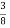 rule
rule 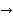
I = 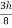
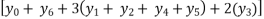
= 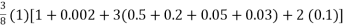
= 1.357
TEXTBOOKS/REFERENCES:
- P. KANDASAMY, K. THILAGAVATHY, K. GUNAVATHI, NUMERICAL METHODS, S. CHAND COMPANY, 2ND EDITION, REPRINT 2012.
- S.S. SASTRY, INTRODUCTORY METHODS OF NUMERICAL ANALYSIS, PHI, 4TH EDITION, 2005.
- ERWIN KREYSZIG, ADVANCED ENGINEERING MATHEMATICS, 9TH EDITION, JOHN WILEY SONS, 2006.
- B.S. GREWAL, HIGHER ENGINEERING MATHEMATICS, KHANNA PUBLISHERS, 35TH EDITION, 2010.