Module 5 B

Numerical method – 2

5.1 ORDINARY DIFFERENTIAL EQUATIONS:

5.2 TAYLOR’S SERIES

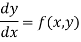
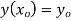
Solve.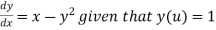

For y(0.1) correct to four and places of decimal using Taylor series method.

Ans. The Taylor's series for y (x) about 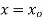is given by

…

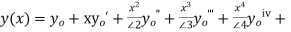Here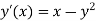

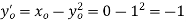
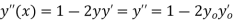
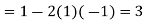
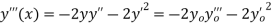
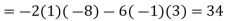
And so on using the value in Taylor's series

To get y(0.1) correct the four place of decimal it is found that the term up to 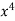are to be taken and other neglected.

Thus y(0.1) = 0.9138

Model questions

Apply Taylor series method to find y(0.2) from 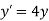given that y(0))=1

5.3 EULER AND MODIFIED EULER’S METHODS.

Euler’s method:-

Given 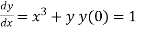compute y (0.02) by Euler’s method taking h=0.01.

Ans. We have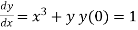

Here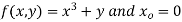

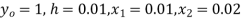
Apply Euler’s method

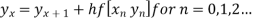
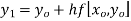
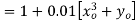
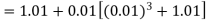
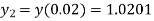
Modified Euler's method

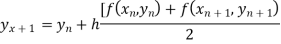
But 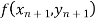which occurs in the right hand side of given equation cannot be calculated since 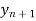is unknown so first we calculate  from Euler's first formula

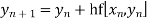
Or

Predicator formula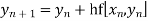

Corrector formula

Using modified Euler's method solved the equation 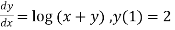for x=1.2 correct to 3 decimal places.

Ans. Given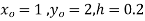

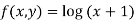
By predictor formula

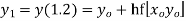
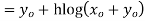
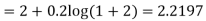
By corrector formula

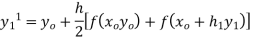
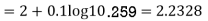
Again, apply character formula

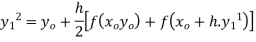
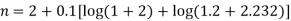
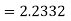
Once again applying the character formula

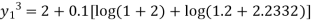
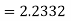
Since 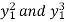takes up to three place of decimal we get y(1.2)=2.2332

5.4 RUNGE- KUTTA METHOD OF FOURTH ORDER FOR SOLVING FIRST AND SECOND ORDER EQUATIONS.

Let equation be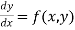

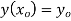
Then,

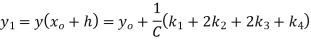
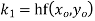
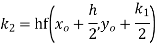
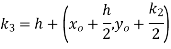
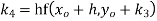
→  Using Runge kutta method of fourth order determine y (0.1) and y(0.2) correct to four decimal place given that 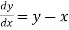where y(0)=2 and h=0.1.

Ans.

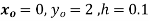
To find y(0.1) we have

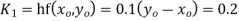
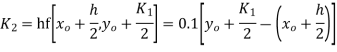
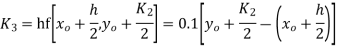
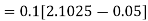
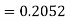
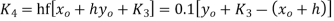
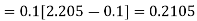
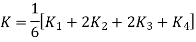
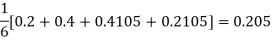
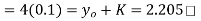
For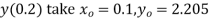

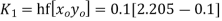
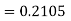
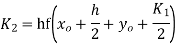
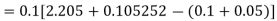
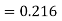
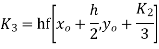
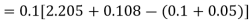
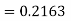
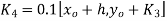
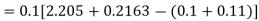
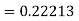
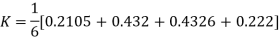
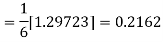
5.5 MILNE’S AND ADAM’S PREDICATOR-CORRECTOR METHODS.

Predictor formula

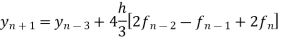
Corrector formula

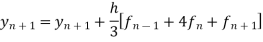
Example. Apply Milne’s method to find solution of differential equation 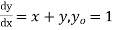 in interval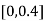

In step of h=0.1 it is given that

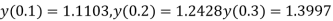
Ans.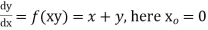

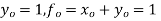
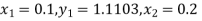
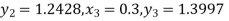
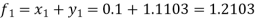
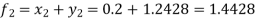
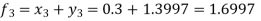
Milne’s Predictor formula

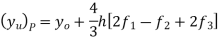
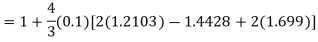
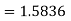
Corrector Formula

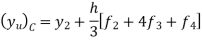
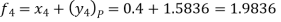
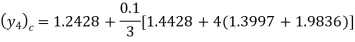
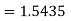
Adam’s Bashtorth method

Predictor Formula

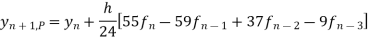
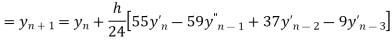
Corrector formula

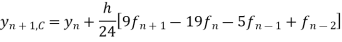
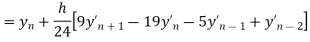
Using Adam’s Bashforth method find y(1.4), given y(1.4) given ,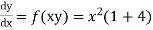

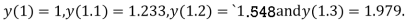
Ans. Given,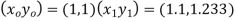

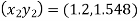
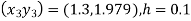
Adam’s Predictor formula

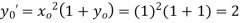
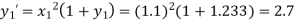
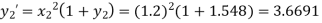
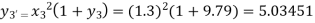
Corrector formula

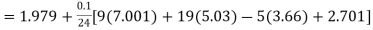
=2.57494

5.6 PARTIAL DIFFERENTIAL EQUATIONS:

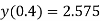
Partial Differential Equation

Forward difference approximately

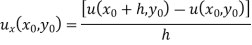
Backward difference equation

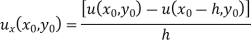
Laplace Equation :- Elliptic type 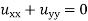is called Laplace equation.

Poisson Equation :-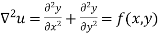  

In this case standard fire point formula is of the form.

Solve the Poisson equation

For the square mesh of the figure given below with u(x,y)=0 on the boundary and mesh length=1

Ans   Here h=1

The standard five-point formula for the given equation is

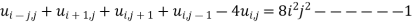
For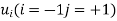

Equation 1 becomes

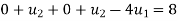
=8(-1)(1)

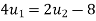         ---2

For 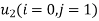equation 1 becomes

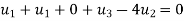
For 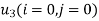equation 1 becomes

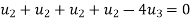
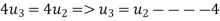
Putting in 1 we get

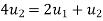
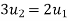
Putting 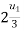for 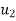in 2 we get

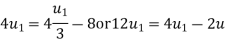
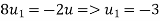
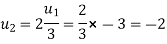
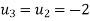
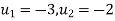
Heat Equation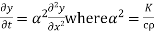

Bender Schmidt method :-

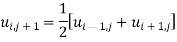
And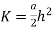

Crank Nicholson Method

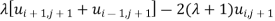
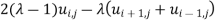
Wave Equation

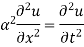
Where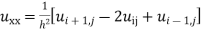  

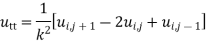
TEXTBOOKS/REFERENCES:

1. P. KANDASAMY, K. THILAGAVATHY, K. GUNAVATHI, NUMERICAL METHODS, S. CHAND & COMPANY, 2ND EDITION, REPRINT 2012.
2. S.S. SASTRY, INTRODUCTORY METHODS OF NUMERICAL ANALYSIS, PHI, 4TH EDITION, 2005.
3. ERWIN KREYSZIG, ADVANCED ENGINEERING MATHEMATICS, 9TH EDITION, JOHN WILEY & SONS, 2006.
4. B.S. GREWAL, HIGHER ENGINEERING MATHEMATICS, KHANNA PUBLISHERS, 35TH EDITION, 2010.