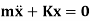Unit - 8
Mechanical Vibrations
Vibration:
“Any motion which repeats itself after an interval of time is called vibration.”
E.g.: Swinging of simple pendulum
Causes of vibration:
Elimination of Vibrations
Elements of Vibratory System
Any vibratory system consists of three elements
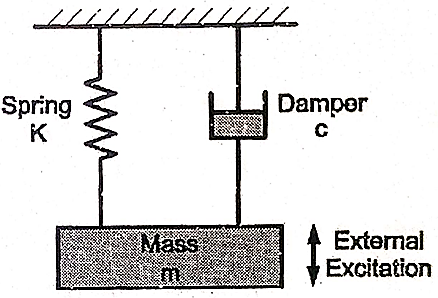
Fig. shows a basic vibratory system. The energy enters the system with the application of external force known as external excitation. Due to excitation mass is disturbed from its mean position and mass starts vibrating between two extreme positions. During this vibrations, potential energy and kinetic energy are converted into one another periodically. Hence, system continues to vibrate.
Now, if some damper is provided to oppose the motion of mass, then some amount of energy is dissipated in each cycle due to damping effect and system decays gradually.
Vector Representation of SHM and basic Terminologies
Simple Harmonic Motion:
Simplest form of periodic motion is harmonic motion and it is called simple harmonic motion (SHM). It can be expressed as
where A is the amplitude of motion, t is the time instant and T is the period of motion.
Harmonic motion is often represented by projection on line of a point that is moving on a circle at constant speed.
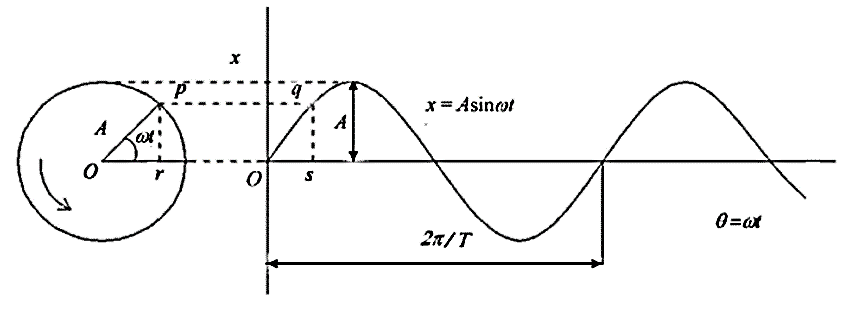
From fig we have,
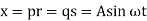
where x is the displacement and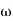 
is the circular frequency in rad/sec
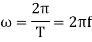
where T is the period (sec) and 
is the frequency (cycle/sec) of the harmonic motion.
The SHM repeats itself in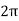 
radians.
Displacement can be expressed as
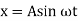
So that the velocity and acceleration can be written as
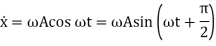
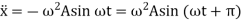
Basic Terminologies
Frequency
Number of cycles per unit time.
Natural Frequency (fn)
Frequency of free vibration of the system.
Expressed in Hz or rad/sec.
Amplitude
The maximum displacement of a vibrating body from its equilibrium position.
Resonance
When the frequency of external excitation is equal to the natural frequency of a vibrating body, the amplitude of vibration becomes excessively large. This concept is known as resonance.
Periodic Motion
A motion which repeats itself after equal intervals of time.
Time Period
Time taken to complete one cycle.
Stiffness of spring (K)
It is the force required to produce unit displacement in the direction of applied force.
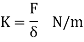
Where,
K = stiffness of spring, N/m
F = force applied on spring, N
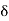= deflection of spring, m
Damping
Damping is the resistance to the motion of the vibrating body, which causes a vibrating body to come to rest or equilibrium position.
Damping Coefficient (c)
Damping coefficient is the damping force or resisting force developed per unit velocity.
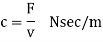
Where,
F = Force applied on damper or damping Force, N
v = Velocity of viscous fluid, m/sec
Fundamental mode of vibration
The fundamental mode of vibration of a system is the mode having the lowest natural frequency.
After disturbing the system, the external excitation is removed, then the system vibrates on its own. This type of vibration is known as free vibrations
e.g.: Simple pendulum.
3 types:-
a) Longitudinal vibrations
When the particles of the shaft or disc move parallel to the axis of the shaft, then the vibrations are known as longitudinal vibrations. In this case the shaft is elongated and shortened alternately and thus the tensile and compressive stresses are induced alternately in the shaft.
b) Transverse vibrations
When the particles of the shaft move approximately perpendicular to the axis of the shaft, then the vibrations are known as transverse vibrations. In this case the shaft is straight and bent alternately and bending stresses are induced in the shaft.
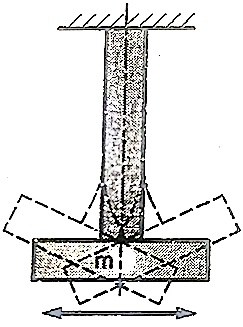
c) Torsional vibrations
When the particles of the shaft move in a circle about the axis of the shaft, then the vibrations are known as torsional vibrations.
In this case the shaft is twisted and untwisted alternately and torsional shear stresses are induced in the shaft to.
2. Forced Vibration
The vibration which is under the influences of external force is called forced vibration.
The external force applied to the body is periodic disturbing force created by unbalance.
The vibrations have the same frequency as the applied force. Due to the application of external forces the amplitude of these vibrations is maintained almost constant.
Many mechanical systems cause vibrations. Also every body or system of bodies or machines have their own natural frequency of vibration. When a body or mechanical system under vibration vibrates with the frequency equal or close to its natural frequency, then it vibrates with amplified amplitude. This condition is called as resonance.
Resonance is the special case of forced vibration. The phenomenon in which the body vibrates under action of external periodic force, whose frequency is equal to the natural frequency of the driven body, so that amplitude becomes maximum is called as Resonance.
Effects of resonance:
When the amplitude becomes maximum of a vibrating body it has various effects on its performance.
Vibrating body or system in resonance condition produces unwanted noise, high stresses, wear, poor reliability, etc.
Due to these severe effects the system or body may have premature failure of one or more of the parts.
Hence, due to these effects, resonance is undesirable. And hence, at the time of design of any system, it is necessary to keep the natural frequency of the system as far as possible from the working frequency of the system.
Few examples of resonance and its effects are discussed below:
The minimum number of independent co-ordinates required to specify the motion of system at any instant is known as degrees of freedom.
It is equal to the number of independent displacements that are possible. This number varies from zero to infinity.
Zero degree of freedom
The body at rest is said to have zero degree of freedom.
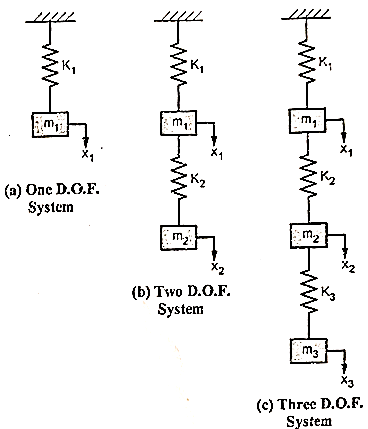
Single Degree of freedom
Here there is only one independent co-ordinate to specify the configuration.
E.g.: A mass supported by a spring.
Two degree of freedom
There are two independent co-ordinates to specify the configuration.
E.g.: Springs supported rigid mass. (It can move in the direction of springs and also have angular motion in one plane)
Multi degrees of freedom
A cantilever beam has infinite degrees of freedom.
A spring mass system as shown in Figure
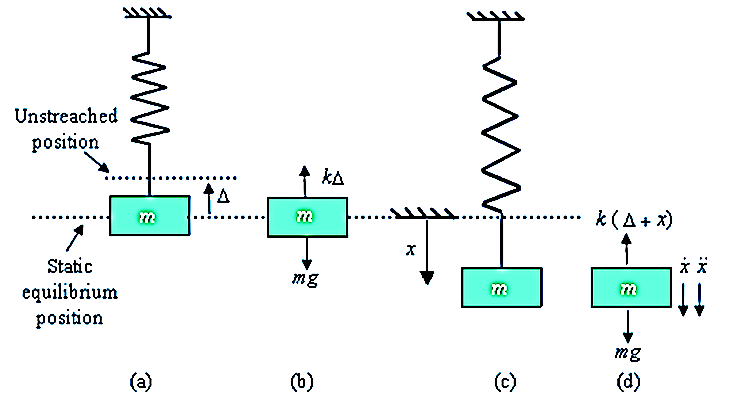
The direction of x in the downward direction is positive. Also, velocity,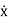 
, acceleration, 
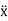, and force, F, are positive in the downward direction
According to D’Alembert’s Principle, a body or a system which is not in static equilibrium due to acceleration it possesses, can be brought to static equilibrium by introducing the inertia force on it.
From Figure (d) on application of Newton's second law, we have
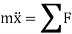
From fig (b) we have
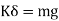
i.e. spring force due to static deflection is equal to weight of the suspended mass
So, the above equation becomes
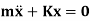
2. D’Alembert’s Method
According to D’Alembert’s Principle, a body or a system which is not in static equilibrium due to acceleration it possesses, can be brought to static equilibrium by introducing the inertia force on it.
By D’Alembert’s Principle
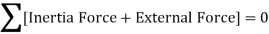
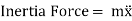
From fig (d)
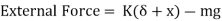
Therefore,
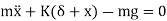
From fig (b) we have
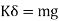
We get,
3. Energy Method
In a conservative system (i.e. with no damping) the total energy is constant, and differential equation of motion can also be established by the principle of conservation of energy.
By law of conservation of energy
Total Energy = Constant
KE + PE = Constant
The equation will be given as
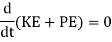
Kinetic Energy is given as
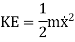
Potential energy PE is stored in the form of strain energy in elastic deformation
Therefore,
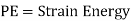
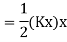
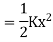
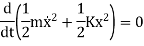
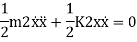
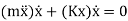
We have equation of motion
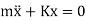
Or
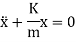
We have fundamental equation of SHM as
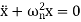
Where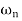 
is the natural frequency (in rads/sec)
By comparing Equation of motion and fundamental equation of SHM, we get
This Equation satisfies the simple harmonic motion condition.
The undamped free vibration executes the simple harmonic motion as shown in Figure
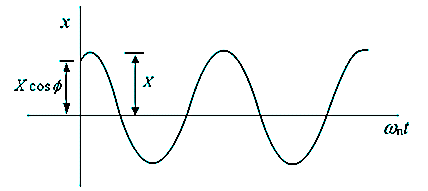
Since sine & cosine functions repeat after 2π radians (i.e. Frequency Time period = 2 π), we have
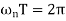
The time period (in second) can be written as
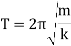
The natural frequency (in rad/sec or Hertz) can be written as
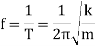
Also we have,
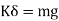
Therefore,
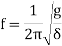
Now, solution for the differential equation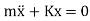 
is
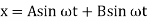
Or
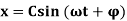
Where,
And
Where, A and B are constants found using the initial conditions.
There are three types of pendulum:
A simple pendulum, consists of heavy mass which is suspended at the end of a light inextensible and flexible string. The other end of the string is fixed to a rigid support O as shown in figure below.
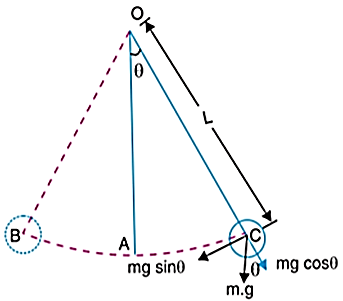
Let L be the length of string and m be the mass of bob suspended at one end of string.
Weight of bob, W = mg
Let the string is suspended through small angle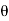 
The couple tending to restore the mass to the equilibrium position A or simply restoring torque is given by,
Since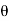 
is very small, 
rad
Hence,
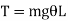
Mass moment of inertia of simple pendulum about an axis through point of suspension O is given by
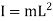
Angular acceleration of string is given by,
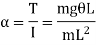
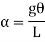
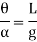
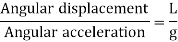
Time period in SHM is given by,
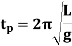
And frequency of oscillation is
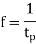
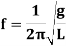
From the above equations, it can be concluded that the periodic time and the frequency of oscillation of a simple pendulum depends only upon its length and acceleration due to gravity. The mass of the bob has no effect on it.
2. Compound Pendulum
When a rigid body is suspended vertically along a fixed point, and it oscillates with a small amplitude under the effect of gravity, the body is known as compound pendulum.
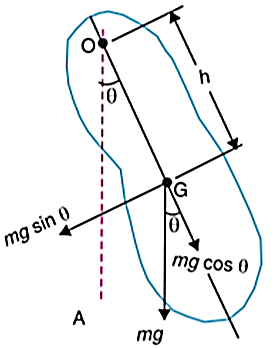
Let,
m = mass of rigid body
k = radius of gyration about axis perpendicular to plane of motion and passing through CG of body
h = distance of CG from point of suspension O
Weight of body, W = mg
If the pendulum is given small angular displacement 
, then couple tending to restore the body in the equilibrium position OA or simply restoring torque is given by,
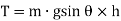
Since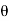 
is very small, 
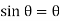rad
Hence,
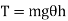
Mass moment of inertia of pendulum about an axis through point of suspension O is given by
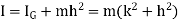
Angular acceleration of string is given by,
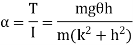
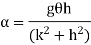
Time period is given by,
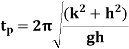
And frequency of oscillation is
3. Torsional Pendulum
It is also referred as trifilar suspension. In torsional pendulum a body (disc or flywheel) is suspended by three long flexible wires A, B and C, as shown in Figure below.
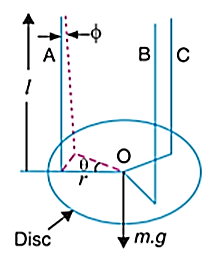
When the body is twisted about its axis through a small angle θ and then released, it will oscillate with simple harmonic motion.
Let,
m = mass of suspended body
W = mg = weight of body
K = radius of gyration of body about an axis perpendicular to plane of motion (twist) and passing from CG of body.
L = length of each wire
r = distance of wire from the axis of disc
= corresponding angular displacement of wire.
Moment of inertia of the body is given by,
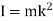
From figure, for small displacements,
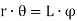
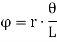
Since the three wires are attached symmetrically with respect to the axis, therefore the tension in each wire will be one-third of the weight of the body.
Hence, tension in each wire is,
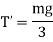
Component of the tension in each wire perpendicular to r
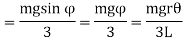
(since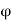 
is very small, 
)
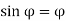Torque applied to each wire to restore the body to its initial equilibrium position (i.e. restoring torque) is
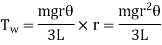
Hence, Total restoring torque applied to three wires is
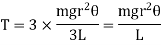
The inertial torque is given by,
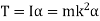
Hence,
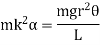
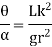
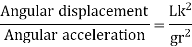
Time period is given by,
And frequency of oscillation is
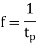
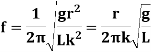
Pendulums has many applications in various fields. Some of the common uses of different pendulums are mentioned below:
2. Use of compound pendulum
3. Use of torsion pendulum
References:
1. Irving H. Shames (2006), Engineering Mechanics, 4th Edition, Prentice Hall
2. F. P. Beer and E. R. Johnston (2011), Vector Mechanics for Engineers, Vol I - Statics, Vol II, – Dynamics, 9th Ed, Tata McGraw Hill
3. R. C. Hibbler (2006), Engineering Mechanics: Principles of Statics and Dynamics, Pearson Press.
4. Andy Ruina and Rudra Pratap (2011), Introduction to Statics and Dynamics, Oxford University Press
5. Shanes and Rao (2006), Engineering Mechanics, Pearson Education
