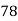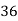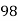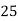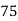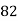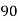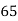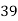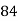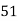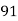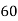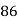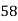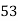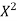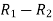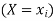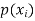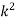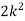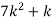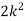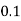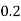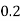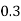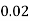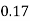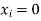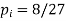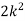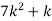Unit – 2
Probability Spaces
A probability space is a three-tuple (S, F, P) in which the three components are
DEFINITIONS:
1. Die: It is a small cube. Dots (number) are marked on its faces. Plural of the die is dice. On throwing a die, the outcome is the number of dots on its upper face.
2. Cards: A pack of cards consists of four suits i.e. Spades, Hearts, Diamonds and Clubs. Each suit consists of 13 cards, nine cards numbered 2, 3, 4, ..., 10, an Ace, a King, a Queen and a Jack or Knave. Colour of Spades and Clubs is black and that of Hearts and Diamonds is red.
Kings, Queens and Jacks are known as face cards.
3. Exhaustive Events or Sample Space: The set of all possible outcomes of a single performance of an experiment is exhaustive events or sample space. Each outcome is called a sample point.
In case of tossing a coin once, S = (H, T) is the sample space. Two outcomes - Head and Tail
- constitute an exhaustive event because no other outcome is possible.
4. Random Experiment: There are experiments, in which results may be altogether different, even though they are performed under identical conditions. They are known as random experiments. Tossing a coin or throwing a die is random experiment.
5. Trial and Event: Performing a random experiment is called a trial and outcome is termed as event. Tossing of a coin is a trial and the turning up of head or tail is an event.
6. Equally likely events: Two events are said to be ‘equally likely’, if one of them cannot be expected in preference to the other. For instance, if we draw a card from well-shuffled pack, we may get any card. Then the 52 different cases are equally likely.
7. Independent events: Two events may be independent, when the actual happening of one does not influence in any way the probability of the happening of the other.
8. Mutually Exclusive events: Two events are known as mutually exclusive, when the occurrence of one of them excludes the occurrence of the other. For example, on tossing of a coin, either we get head or tail, but not both.
9. Compound Event: When two or more events occur in composition with each other, the simultaneous occurrence is called a compound event. When a die is thrown, getting a 5 or 6 is a compound event.
10. Favourable Events: The events, which ensure the required happening, are said to be favourable events. For example, in throwing a die, to have the even numbers, 2, 4 and 6 are favourable cases.
11. Conditional Probability: The probability of happening an event A, such that event B has already happened, is called the conditional probability of happening of A on the condition that B has already happened. It is usually denoted by 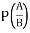
12. Odds in favour of an event and odds against an event: If number of favourable ways = m, number of not favourable events = n
(i) Odds in favour of the event 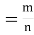
(ii) Odds against the event 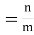
13. Classical Definition of Probability. If there are N equally likely, mutually, exclusive and exhaustive of events of an experiment and m of these are favourable, then the probability of the happening of the event is defined as 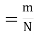
Consider Example1: In poker, a full house (3 cards of one rank and two of another, e.g. 3 fours and 2 queens) beats a flush (five cards of the same suit).
A player is more likely to be dealt a flush than a full house. We will be able to precisely quantify the meaning of “more likely” here.
Example2: A coin is tossed repeatedly.
Each toss has two possible outcomes:
Heads (H) or Tails (T)
Both equally likely. The outcome of each toss is unpredictable; so is the sequence of H and T.
However, as the number of tosses gets large, we expect that the number of H (heads) recorded will fluctuate around of the total number of tosses. We say the probability of aH is
of the total number of tosses. We say the probability of aH is , abbreviated by
, abbreviated by . Of course
. Of course 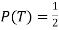 also
also
Example3:
If 4 coins are tossed, what is the probability of getting 3 heads and 1 tail?
NOTES:
• In general, an event has associated to it a probability, which is a real number between 0 and 1.
• Events which are unlikely have low (close to 0) probability, and events which are likely have high (close to 1) probability.
• The probability of an event which is certain to occur is 1; the probability of an impossible event is 0.
Let A and B be two events of a sample space Sand let  . Then conditional probability of the event A, given B, denoted by
. Then conditional probability of the event A, given B, denoted by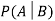 is defined by –
is defined by –
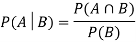
Theorem: If the events A and B defined on a sample space S of a random experiment are independent, then
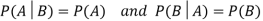
Example1: A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.
SOLUTION: We consider the following events:
A: Selected item comes from A.
B: Selected item comes from B.
D: Selected item is defective.
We are looking for  . We know:
. We know:

Now,
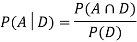
So we need

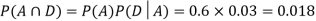
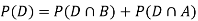
Since, D is the union of the mutually exclusive events  and
and 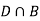 (the entire sample space is the union of the mutually exclusive events A and B)
(the entire sample space is the union of the mutually exclusive events A and B)
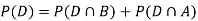
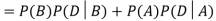
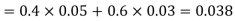
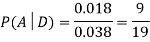
Example2: Two fair dice are rolled, 1 red and 1 blue. The Sample Space is
S = {(1, 1),(1, 2), . . . ,(1, 6), . . . ,(6, 6)}.Total -36 outcomes, all equally likely (here (2, 3) denotes the outcome where the red die show 2 and the blue one shows 3).
(a) Consider the following events:
A: Red die shows 6.
B: Blue die shows 6.
Find 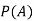 ,
, 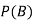 and
and 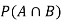 .
.
Solution: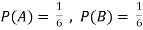
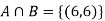
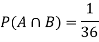
NOTE: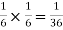 so
so 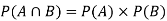 for this example. This is not surprising - we expect A to occur in
for this example. This is not surprising - we expect A to occur in  of cases. In
of cases. In  of these cases i.e. in
of these cases i.e. in 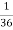 of all cases, we expect B to also occur.
of all cases, we expect B to also occur.
(b) Consider the following events:
C: Total Score is 10.
D: Red die shows an even number.
Find 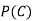 ,
, 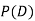 and
and 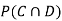 .
.
Solution:
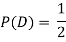
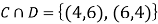
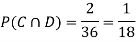
NOTE: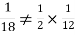 so,
so, .
.
Why does multiplication not apply here as in part (a)?
ANSWER: Suppose C occurs: so the outcome is either (4, 6), (5, 5) or (6, 4). In two of these cases, namely (4, 6) and (6, 4), the event D also occurs. Thus
Although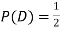 , the probability that D occurs given that C occurs is
, the probability that D occurs given that C occurs is  .
.
We write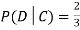 , and call
, and call 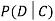 the conditional probability of D given C.
the conditional probability of D given C.
NOTE: In the above example
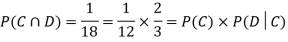
Example3: Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball drawn is red find the probability that it is drawn from the first urn.
Solution:
 :The ball is drawn from urnI.
:The ball is drawn from urnI.
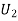 : The ball is drawn from urnII.
: The ball is drawn from urnII.
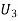 : The ball is drawn from urnIII.
: The ball is drawn from urnIII.
R:The ball is red.
We have to find 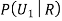
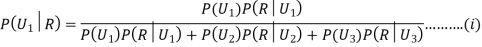
Since the three urns are equally likely to be selected
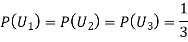
Also,
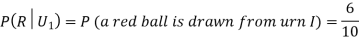
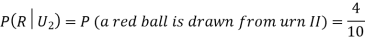
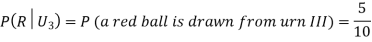
From (i), we have
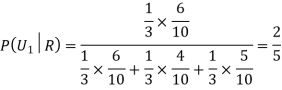
Independence:
Two events A, B ∈ are statistically independent iff
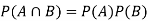
(Two disjoint events are not independent.)
Independence implies that

Knowing that outcome is in B does not change your perception of the outcome’s being in A.
Random Variable: It is a real valued function which assign a real number to each sample point in the sample space.
A random variable X is a function defined on the sample space 5 of an experiment S of an experiment. Its value are real numbers. For every number a the probability
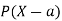
With which X assumes a is defined. Similarly for any interval l the probability
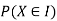
With which X assumes any value in I is defined.
Example: 1. Tossing a fair coin thrice then-
Sample Space(S) = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
2. Roll a dice
Sample Space(S) = {1,2,3,4,5,6}
Discrete Random Variable:
A random variable which takes finite or as most countable number of values is called discrete random variable.
Discrete Random Variables and Distribution
By definition a random variable X and its distribution are discrete if X assumes only finitely maany or at most contably many values 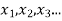 called the possible values of X. with positive probabilities
called the possible values of X. with positive probabilities 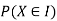 is zero for any interval J containing no possible values.
is zero for any interval J containing no possible values.
Clearly the discrete distribution of X is also determined by the probability functions f (x) of X, defined by
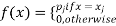
From this we get the values of the distribution function F (x) by taking sums.
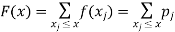
Example: 1. No. of head obtained when two coin are tossed.
2. No. of defective items in a lot.
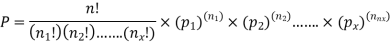
Example1:
You are given a bag of marble. Inside the bag are 5 red marble, 4 white marble, 3 blue marble. Calculate the probability that with 6 trials you choose 3 marbles that are red, 1 marble that is white and 2 marble is blue. Replacing each marble after it is chosen.
Solution:
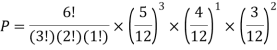
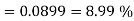
Example2:
You are randomly drawing cards from an ordinary deck of cards. Every time you pick one you place it back in the deck. You do this 5 times. What is the probability of drawing 1 heart, 1 spade, 1club, and 2 diamonds?
Solution:

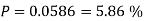
Example3:
A die weighed or loaded so that the number of spots X that appear on the up face when the die is rolled has pmf
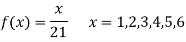
If this loaded die is rolled 21 times. Find the probability of rolling one one, two twos, three threes, four fours, five fives, six sixes.
Solution:

Poisson distribution
If it is a distribution related to the probabilities of events which are extremely rare but which have a large number of independent opportunities for occurrence. The number of persons born blind per year in a large city and the number of deaths by horse cake in an army corps are some of the phenomenon in which this law is followed.
this distribution can be derived as a limiting case of the binomial distribution of making a very large and p very small, keeping up fixed (=m, say).
The probability of r successes in a binomial distribution is
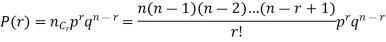
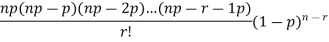
As 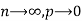 (np=m), we have
(np=m), we have
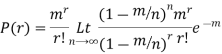
So that the probability of 0,1,2…,r,… successors in a Poisson distribution are given by
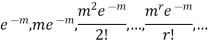
The sum of these probabilities is unity as it should be.
(2) Constants of the Poisson distribution
These constants can easily be derived from the corresponding constants of the binomial distribution simply by making and noting that np =m
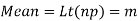
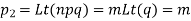
Standard deviation 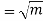
Also 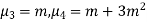
Skewness 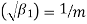 , Kurosis
, Kurosis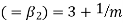
Since 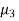 is positive, Poisson distribution is positively skewed and since
is positive, Poisson distribution is positively skewed and since 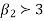 , it is Leptokurtic.
, it is Leptokurtic.
(3) Applications of poison distribution.
The distribution is applied to problems concerning:-
(i) Arrival pattern of defective vehicles in a workshop, patients in a hospital or telephone calls.
(ii) Demand pattern for certain spare parts.
(iii) Number of fragments from a shell hitting a target.
(iv) Spatial distribution of bomb hits.
Example. If the probability of a bad reaction from a certain injection is 0.001, determine the chance that out of 2,000 individuals more than to get a bad reaction.
Solution. It follows a Poisson distribution as the probability of occurrence is very small
Mean m = np = (0.001)=2
Probability that more than two will get bad reaction
= 1- [probability that no one get a bad reaction + probability that one gets a bad reaction + probability that to get bad reaction]
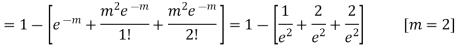

Example. In a certain factory turning out razor blades there is a small chance of 0.002 of any need to be defective. The blades are supplied in packets of 10, use Poisson distribution to calculate the approximate number of packets containing no defective, one defective and to defective blades respectively in a consignment of 10000 packets.
Solution. We know that m = no = 10 × 0.002=0.02
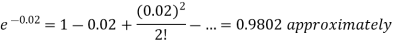
Probability of no defective blade is 
Therefore number of packets containing no defective blade is
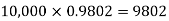
Similarly the number of packets containing one defective blade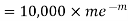
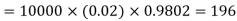
Find the number of packets containing to defective blades
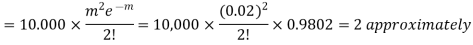
Example. Fit a Poisson distribution to the set of observations:
x | 0 | 1 | 2 | 3 | 4 |
f | 122 | 60 | 15 | 2 | 1 |
Solution. Mean = 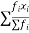
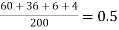
Therefore mean of Poisson distribution i.e. m =0.5
Hence the theoretical frequency for r successes is is
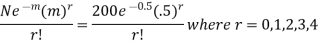
Therefore the theoretical frequencies are
x | 0 | 1 | 2 | 3 | 4 |
f | 121 | 61 | 16 | 2 | 0 |
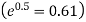
A random experiment whose results are of only two types, for example, success S and failure F, is a Bernoulli test. The probability of success is taken as p, while the probability of failure is q = 1 - p. Consider a random experiment of items in a sale, either sold or not sold. An item produced may be defective or non-defective. An egg is boiled or un-boiled.
A random variable X will have the Bernoulli distribution with probability p if its probability distribution is
P(X = x) = px (1 – p)1−x, for x = 0, 1 and P(X = x) = 0 for other values of x.
Here, 0 is failure and 1 is success.
Conditions for Bernoulli tests
1. A finite number of tests.
2. Each trial must have exactly two results: success or failure.
3. The tests must be independent.
4. The probability of success or failure must be the same in each test.
Problem 1:
If the probability that a light bulb is defective is 0.8, what is the probability that the light bulb is not defective?
Solution:
Probability that the bulb is defective, p = 0.8
Probability that the bulb is not defective, q = 1 - p = 1 - 0.8 = 0.2
Problem 2:
10 coins are tossed simultaneously where the probability of getting heads for each coin is 0.6. Find the probability of obtaining 4 heads.
Solution:
Probability of obtaining the head, p = 0.6
Probability of obtaining the head, q = 1 - p = 1 - 0.6 = 0.4
Probability of obtaining 4 of 10 heads, P (X = 4) = C104 (0.6) 4 (0.4) 6P (X = 4) = C410 (0.6) 4 (0.4) 6 = 0.111476736
Problem 3:
In an exam, 10 multiple-choice questions are asked where only one in four answers is correct. Find the probability of getting 5 out of 10 correct questions on an answer sheet.
Solution:
Probability of obtaining a correct answer, p = 1414 = 0.25
Probability of obtaining a correct answer, q = 1 - p = 1 - 0.25 = 0.75
Probability of obtaining 5 correct answers, P (X = 5) = C105 (0.25) 5 (0.75) 5C510 (0.25) 5 (0.75) 5 = 0.05839920044
Independent random variables
In real life, we usually need to deal with more than one random variable. For example, if you study physical characteristics of people in a certain area you might pick a person at random and then look at his/ her weight, height etc. the weight of the randomly chosen person is one random variable while his/ her height is another one. Not only do we need to study is random variable separately but also we need to consider if there is dependence (i.e. correlation) between them. is it true that a taller person is more likely to be heavier or not? the issues of dependence between several random variables will be studied in detail later on, but here we would like to talk about special scenario where two random variables are independent.
The concept of independent random variables is very similar to independent events. Remember to A and B are independent if we have P (A,B) = P (A) P (B) (remember comma means and, i.e. P(A,B) = P (A and B) = P (A 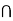 B). Similarly we have the following definition for independent discrete random variables.
B). Similarly we have the following definition for independent discrete random variables.
Definition
Consider two discrete random variables X and Y. We say that X and Y are independent if

In general if two random variables are independent then you can write
 , For all sets A and B
, For all sets A and B
Definition
Consider n discrete random variables 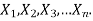 We say that
We say that  are independent if
are independent if
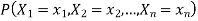
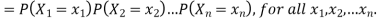
Example.
I toss a coin twice and define X to be the number of heads one observe. Then I toss the coin two more times and define Y to be the number of heads that I observed this time. Find 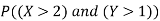
Solution. since X and Y are the result of different independent coin tosses the two random variables X and Y are independent.

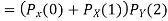

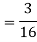
Example. A box A contains 2 white and 4 Black balls. Another box B contains 5 white and 7 black balls. A ball is transferred from the box A to the box B. Then A ball is drawn from the box B. Find the probability that it is white.
Solution. The probability of drawing a white ball from box B will depend on whether the transferred ball is black or white.
If black ball is transferred, it's probability is 4/6. There are now 5 white and 8 black balls in the box B.
Then the probability of drawing a white ball from box B is 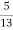
Thus the probability of drawing a white ball from B, if the transferred ball is black
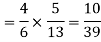
Similarly the probability of drawing a white ball from urn B if the transferred ball is white
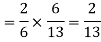
Hens required probability 
Example. (a) A biased coin is tossed till a head appears for the first time. What is the probability that the number of required tosses is odd?
(b) Two persons A and B toss an unbiased coin alternately on the understanding that the first two who get the head wins. If A starts the game, find their respective chances of winning.
Solution. (a) Let p be the probability of getting a head and q the probability of getting a tail in a single toss, so that p + q=1.
Then probability of getting head on an odd toss = probability of getting gead in the 3rd toss + probability of getting head in the 5th toss +…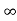
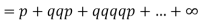
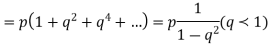
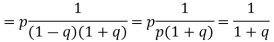
(b) Probability of getting head = 1/2. Then A can win in 1st, 3rd, 5th,…throws.
The chances of A’s winning = 
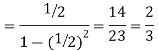
Hence the chances of B’s winning=
Example. A pair of dice is tossed twice. Find the probability of scoring 7 points
(a) Once
(b) At least once
(c) Twice
Solution. In a single toss of two dice the sum 7 can be obtained as (1,6), (2,5), (3,4), (4,3), (5,2), (6,1), i.e. in 6 ways so that the probability of getting 7 = 6/36 = 1/6
Also the probability of not getting 7 = 1-1/6= 5/6
(a) The probability of getting seven in the first toss and not getting 7 in the second toss=1/6×5/6=5/36
Similarly the probability off not getting seven in the first toss and getting 7:00 in the second toss=5/6×1/6=5/36
Since these mutually exclusive events addition law of probability applies
Required probability 
(b) The probability of not getting 7 in either toss
Therefore the probability of getting 7 at least once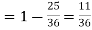
(c) The probability of getting 7 twice 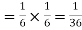
Example. Two cards are drawn in succession from a pack of 52 cards. Find the chance that the first is a king and the second a queen if the first card is
(i) Replaced
(ii) Got replaced
Solution. (i) the probability of drawing a king 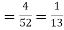
if the card is replaced the back will again have 52 cards so that the probability of drawing a queen is 1/13.
The two events being independent the probability of drawing both cards in succession 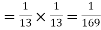
(ii)the probability of drawing a king = 1/13
If the card is not replaced the pack will have 51 cards only so that the chance of drawing the queen is 4/51.
Hence the probability of drawing both cards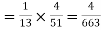
Example. Two cards are selected at random from 10 cards numbered 1to10 find the probability p that the sum is odd if
(i) The two cards are drawn together
(ii) the two cards are drawn one after the other without replacement
(iii) The two cards are drawn one after the other with replacement
Solution. (i) two cars out of 10 can be selected in 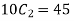 ways. The sum is odd if one number is odd and other number is even. There being 5 odd numbers (1,3,5,7,9) and 5 even numbers (2,4,6,8,10) an what and an even number is chosen in 5×5=25 ways.
ways. The sum is odd if one number is odd and other number is even. There being 5 odd numbers (1,3,5,7,9) and 5 even numbers (2,4,6,8,10) an what and an even number is chosen in 5×5=25 ways.
Thus, 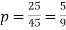
(ii)two cards out of 10 can be selected one of the other without replacing in 10 × 10 = 100 ways
An odd number is selected in 5 × 5 =25 ways and an even number in 5 × 5 = 25 ways
Thus 
(iii)two cards can be selected one after the other with replacement in 10 × 10 =100 ways
An odd number is selected in 5 × 5 =25 ways and an even number in 5×5=25 ways
Thus, 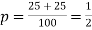
Discrete random variables and distributions
By definition a random variable X and its distribution are discrete if X resumes only finitely many or at most countably many values  whereas the probability
whereas the probability 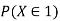 is zero for any interval I containing no possible value. Clearly the discrete distribution of X is also determined by the probability function f (x) of X, defined by
is zero for any interval I containing no possible value. Clearly the discrete distribution of X is also determined by the probability function f (x) of X, defined by

From this we get the value of the distribution function F (x) by taking sums
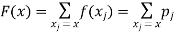
Expectation
The mean value (μ) of the probability distribution of a variate X is commonly known as its expectation current is denoted by E (X). If f(x) is the probability density function of the variate X, then
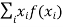 (discrete distribution)
(discrete distribution)
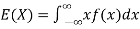 (continuous distribution)
(continuous distribution)
In general expectation of any function is 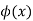 given by
given by
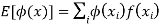 (discrete distribution)
(discrete distribution)
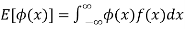 (continuous distribution)
(continuous distribution)
(2) Variance offer distribution is given by
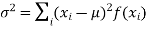 (discrete distribution)
(discrete distribution)
 (continuous distribution)
(continuous distribution)
Where 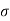 is the standard deviation of the distribution.
is the standard deviation of the distribution.
(3) The rth moment about mean (denoted by 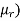 is defined by
is defined by
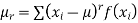 (discrete function)
(discrete function)
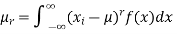 (continuous function)
(continuous function)
(4) Mean deviation from the mean is given by
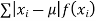 (discrete distribution)
(discrete distribution)
 (continuous distribution)
(continuous distribution)
Example. In a lottery, m tickets are drawn at a time out of a tickets numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.
Solution. Let  be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
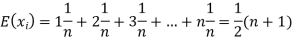
Therefore expected value of the sum of the numbers on the tickets drawn
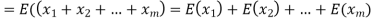

Example. X is a continuous random variable with probability density function given by
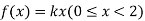

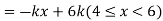
Find k and mean value of X.
Solution. Since the total probability is unity.

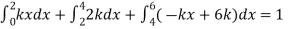
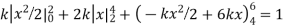
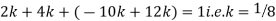
Mean of X =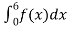
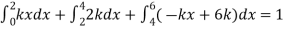
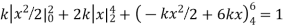
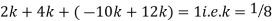
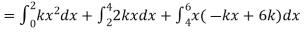
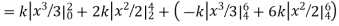
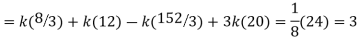
Example. The frequency distribution of a measurable characteristic varying between 0 and 2 is as under
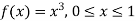
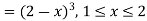
Calculate two standard deviation and also the mean deviation about the mean.
Solution. Total frequency N =
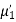 (about the origin)=
(about the origin)=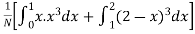
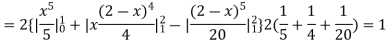
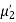 (about the origin)=
(about the origin)= 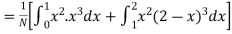
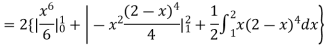
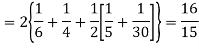
Hence, 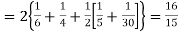
i.e., standard deviation 
Mean derivation about the mean
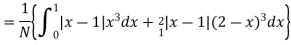

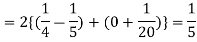
Moment generating function
(1) The moment generating function (m.g.f) of the discrete probability distribution of the variate X about the value x = a is defined as the expected value of 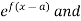 is denoted by
is denoted by 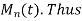

Which is a function of the parameters t only.
Expanding the exponential in (1) we get
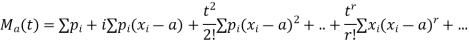
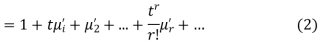
Where  is the moment of order r and a. Thus
is the moment of order r and a. Thus 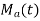 generates moment and that is why it is called the moment generating function. From (2) we find
generates moment and that is why it is called the moment generating function. From (2) we find
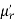 = coefficient of
= coefficient of  In the expansion of
In the expansion of 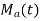
Otherwise differentiating (2) r X with respect to t and then putting t = 0, we get
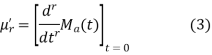
Thus the moment about any point x = a can be found from (2) or more conveniently from the formula (3).
Rewriting (1) as
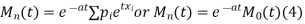
Thus the m.g.f about point 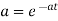 (m.g.f about the origin).
(m.g.f about the origin).
(2) If f(x) is the density function of a continuous variate X then the moment generating function of this continuous probability distribution about x =a is given by
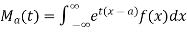
Example. Find the moment generating function of the exponential distribution 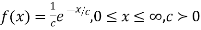 . Hence find its mean and S.D.
. Hence find its mean and S.D.
Solution. The moment generating function about the origin is
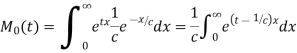
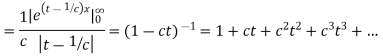

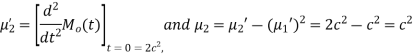
Hence the mean is c wand S.D. is also c.
Variance of a sum
One of the applications of covariance is finding the variance of a sum of several random variables. In particular, if Z = X + Y, then
Var (Z) =Cov (Z, Z)

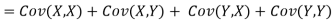

More generally, for a, b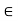 R we conclude
R we conclude
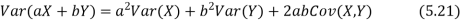
Variance
Consider two random variables X and Y with the following PMFs
 (3.3)
(3.3)
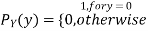 (3.4)
(3.4)
Note that EX =EY = 0. Although both random variables have the same mean value, their distribution is completely different. Y is always equal to its mean of 0, while X is IDA 100 or -100, quite far from its mean value. The variance is a measure of how spread out the distribution of a random variable is. Here the variance of Y is quite small since its distribution is concentrated value. Why the variance of X will be larger since its distribution is more spread out.
The variance of a random variable X with mean 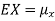 , is defined as
, is defined as
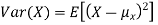
By definition the variance of X is the average value of 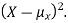 Since
Since 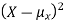 ≥0, the variance is always larger than or equal to zero. A large value of the variance means that
≥0, the variance is always larger than or equal to zero. A large value of the variance means that  is often large, so X often X value far from its mean. This means that the distribution is very spread out. on the other hand a low variance means that the distribution is concentrated around its average.
is often large, so X often X value far from its mean. This means that the distribution is very spread out. on the other hand a low variance means that the distribution is concentrated around its average.
Note that if we did not square the difference between X and its mean the result would be zero. That is
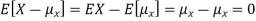
X is sometimes below its average and sometimes above its average. Thus  is sometimes negative and sometimes positive but on average it is zero.
is sometimes negative and sometimes positive but on average it is zero.
To compute 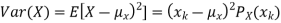 , note that we need to find the expected value of
, note that we need to find the expected value of 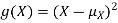 , so we can use LOTUS. In particular we can write
, so we can use LOTUS. In particular we can write
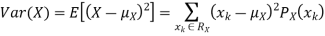
For example, for X and Y defined in equations 3.3 and 3.4 we have
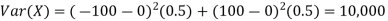
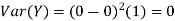
As we expect, X has a very large variance while Var (Y) = 0
Note that Var (X) has a different unit than X. For example, if X is measured in metres then Var(X) is in 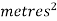 .to solve this issue we define another measure called the standard deviation usually shown as
.to solve this issue we define another measure called the standard deviation usually shown as 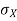 which is simply the square root of variance.
which is simply the square root of variance.
The standard deviation of a random variable X is defined as
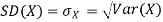
The standard deviation of X has the same unit as X. For X and Y defined in equations 3.3 and 3.4 we have

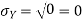
Here is a useful formula for computing the variance.
Computational formula for the variance
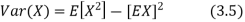
To prove it note that
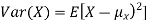
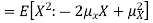
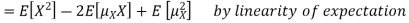
Note that for a given random variable X,  is just a constant real number. Thus
is just a constant real number. Thus 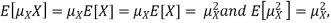 so we have
so we have
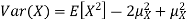

Equation 3.5 is equally easier to work with compared to 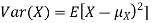 . To use this equation we can find
. To use this equation we can find 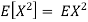 using LOTUS.
using LOTUS.
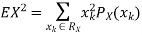
And then subtract  to obtain the variance.
to obtain the variance.
Example. I roll a fair die and let X be the resulting number. Find EX, Var(X), and 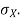
Solution. We have 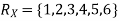 and
and 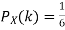 for k = 1,2,…,6. Thus we have
for k = 1,2,…,6. Thus we have

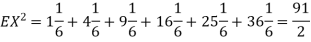
Thus , 
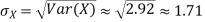
Theorem
For random variable X and real number a and b
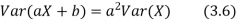
Proof. If 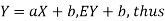
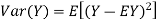
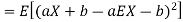

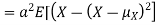
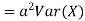
From equation 3.6, we conclude that, for standard deviation, 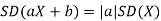 . We mentioned that variance is NOT a linear operation. But there is a very important case, in which variance behave like a linear operation and that is when we look at sum of independent random variables,
. We mentioned that variance is NOT a linear operation. But there is a very important case, in which variance behave like a linear operation and that is when we look at sum of independent random variables,
Theorem
If 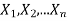 are independent random variables and
are independent random variables and 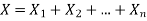 , then
, then
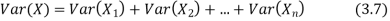
Example. If 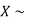 Binomial (n, p) find Var (X).
Binomial (n, p) find Var (X).
Solution. We know that we can write a Binomial (n, p) random variable as the sum of n independent Bernoulli (p) random variable, i.e. 
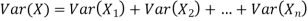
If 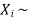 Bernoulli (p) then its variance is
Bernoulli (p) then its variance is
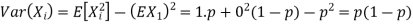
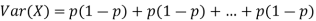
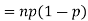
Problem. If 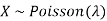 , find Var (X).
, find Var (X).
Solution. We already know 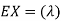 , thus Var (X)
, thus Var (X) . You can find
. You can find 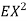 directly using LOTUS, however, it is a little easier to find E [X (X-1)] first. In particular using LOTUS we have
directly using LOTUS, however, it is a little easier to find E [X (X-1)] first. In particular using LOTUS we have
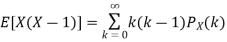
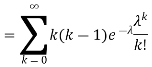
S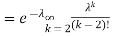


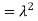
So we have  . Thus,
. Thus, 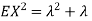 and we conclude
and we conclude
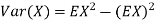

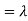
Whenever two variables x and y are so related that an increase in the one is accompanied by an increase or decrease in the other, then the variables are said to be correlated.
For example, the yield of crop varies with the amount of rainfall.
If an increase in one variable corresponds to an increase in the other, the correlation is said to be positive. If increase in one corresponds to the decrease in the other the correlation is said to be negative. If there is no relationship between the two variables, they are said to be independent.
Perfect Correlation: If two variables vary in such a way that their ratio is always constant, then the correlation is said to be perfect.
KARL PEARSON’S COEFFICIENT OF CORRELATION:
r between two variables x and y is defined by the relation
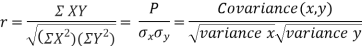
Where, X = x –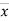 , Y = y –
, Y = y –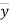
i.e. X, Y are the deviations measured from their respective means,

Example: Ten students got the following percentage of marks in Economics and Statistics
Calculate the 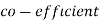 of correlation.
of correlation.
Roll No. |
|
|
|
|
|
|
|
|
|
|
Marks in Economics |
|
|
|
|
|
|
|
|
|
|
Marks in |
|
|
|
|
|
|
|
|
|
|
Solution: Let the marks of two subjects be denoted by 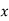 and
and 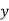 respectively.
respectively.
Then the mean for 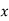 marks
marks 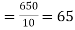 and the mean ofy marks
and the mean ofy marks 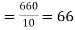
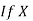 and
and 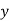 are deviations of x’s and
are deviations of x’s and 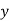 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | y | X=x=65 | Y=y=66 |
|
| XY |
78 | 84 | 13 | 18 | 169 | 234 | 234 |
36 | 51 | -29 | -15 | 841 | 225 | 435 |
98 | 91 | 33 | 1089 | 1089 | 625 | 825 |
25 | 60 | -40 | 1600 | 1600 | 36 | 240 |
75 | 68 | 10 | 100 | 100 | 4 | 20 |
82 | 62 | 17 | 289 | 289 | 16 | -68 |
90 | 86 | 25 | 625 | 625 | 400 | 500 |
62 | 58 | -3 | 9 | 9 | 64 | 24 |
65 | 53 | 0 | 0 | 0 | 169 | 0 |
39 | 47 | -26 | 676 | 676 | 361 | 494 |
650 | 660 | 0 | 5398 | 5398 | 2224 | 2704 |
Here, 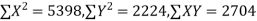
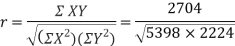
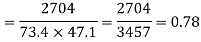
Spearman’s Rank Correlation
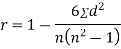
Solution: Let 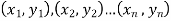 be the ranks of
be the ranks of 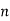 individuals corresponding to two characteristics.
individuals corresponding to two characteristics.
Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3,  and hence their arithmetic means are, each
and hence their arithmetic means are, each
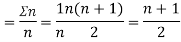
Let 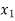 ,
, 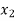 ,
, 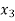 ,
,  be the values of variable
be the values of variable 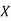 and
and 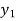 ,
, 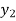 ,
, 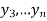 those of
those of 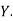
Then 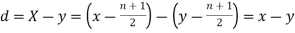
where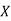 and y are deviations from the mean.
and y are deviations from the mean.
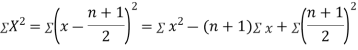
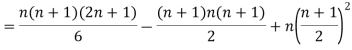
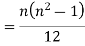
Clearly, 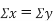 and
and 
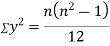

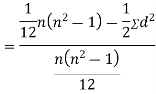
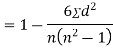
SPEARMAN’S RANK CORRELATION COEFFICIENT:

where  denotes rank coefficient of correlation and
denotes rank coefficient of correlation and  refers to the difference ofranks between paired items in two series.
refers to the difference ofranks between paired items in two series.
Example: Compute Spearman’s rank correlation coefficient r for the following data:
Person | A | B | C | D | E | F | G | H | I | J |
Rank Statistics | 9 | 10 | 6 | 5 | 7 | 2 | 4 | 8 | 1 | 3 |
Rank in income | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Solution:
Person | Rank Statistics | Rank in income | d= |
|
A | 9 | 1 | 8 | 64 |
B | 10 | 2 | 8 | 64 |
C | 6 | 3 | 3 | 9 |
D | 5 | 4 | 1 | 1 |
E | 7 | 5 | 2 | 4 |
F | 2 | 6 | -4 | 16 |
G | 4 | 7 | -3 | 9 |
H | 8 | 8 | 0 | 0 |
I | 1 | 9 | -8 | 64 |
J | 3 | 10 | -7 | 49 |
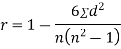
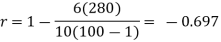
Example: If X and Y are uncorrelated random variables, 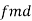 the
the 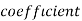 of correlation between
of correlation between 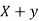 and
and 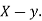
Solution:
Let 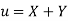 and
and 
Then 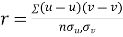
Now 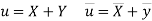
Similarly 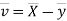
Now 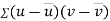
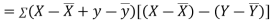
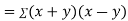


Also 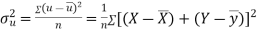
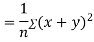
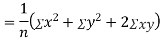
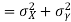 (As
(As 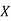 and
and  are not correlated, we have
are not correlated, we have 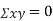 )
)
Similarly 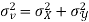

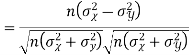
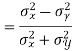
Markov and Chebyshev Inequalities
Let X be any positive continuous random variable, we can write
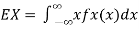
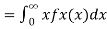
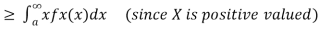
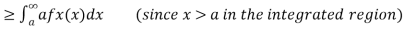

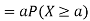
Thus, we conclude
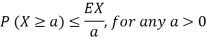
We can prove the above inequality for discrete or mixed random variables similarly (using the generalized PDF), so we have the following result called Markov's inequality.
Markov Inequality
If X is any non negative random variable then
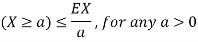
Example 1. Prove the union bound using Markov's inequality.
Solution. Similar to the discussion in the previous section, let 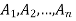 be any events and X be the number events
be any events and X be the number events 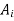 that occur. We saw that
that occur. We saw that
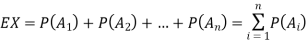
Since X is a non negative random variable we can apply Markov's inequality. Choosing a = 1, we have
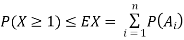
But note that 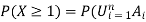 )
)
Example 2. Let X ~ binomial (n, p). Using Markov's inequality, find an upper bound on P(X ≥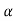 n), where
n), where 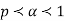 . Evaluate the ground for
. Evaluate the ground for 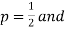
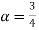
Solution. Note that X is a non negative random variable and EX = np. Applying Markov's inequality we obtain
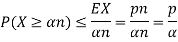
For 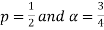 ,we obtain
,we obtain
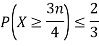
Chebyshev's Inequality
Let X be any random variable. If you define 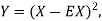 then Y is a nonnegative random variable so we can apply Markov''s inequality to Y. In particular for any positive real number b, we have
then Y is a nonnegative random variable so we can apply Markov''s inequality to Y. In particular for any positive real number b, we have
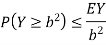
But note that
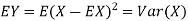
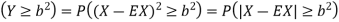
Thus we conclude that
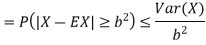
This is Chebyshev’s inequality.
Chebyshev’s inequality
If X is any random variable then for any b>0 we have
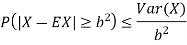
Chebyshev’s inequality states that the difference between X and EX is somehow limited by Var (X). This is intuitively expected as variance shows on average how far we are from the mean.
Example. Let X ~ binomial (n, p). Using Chebyshev's inequality, find an upper bound on P(X ≥n), where 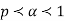 . Evaluate the ground for
. Evaluate the ground for 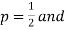

Solution. One way to obtain a bound is to write
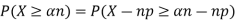
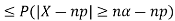

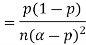
For p = ½ and 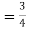 , we obtain
, we obtain
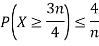
Example. Let X be a random variables such that
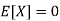

Find a lower bound to its variance.
Solution.
The lower bound can be derived thanks to Chebyshev’s inequality


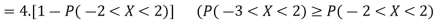
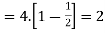
Thus, the lower bound is Var[X]≥2
A continuous random variable is a random variable where the data can take infinitely many values. For example, a random variable measuring the time taken for something to be done is continuous since there are an infinite number of possible times that can be taken.
Continuous random variable is called by a probability density function p (x), with given properties: p (x) ≥ 0 and the area between the x-axis & the curve is 1: ... standard deviation of a variable Random is defined by σ x = √Variance (x).
∫-∞∞ p(x) dx = 1.
sx2 = (x1 - x)2 + ... + (xn - x)2

n – 1
10. If x1, x2, ... , xn are explanations since a random sample, the sample standard deviation s is known the square root of variance:
sx =√(x1 - x)2 + ... + (xn - x)2

n – 1
11. Sample Co-variance of x1, x2, ..., xn is known-
sxy = (x1 - x)(y1 - y) + ... + (xn - x)(yn - y)

n - 1
12. A random vector is a column vector of random variable.
v = (x1 ... xn)T
13. Expected value of Random vector E(v) is known byvector of expected value of component.
If v = (x1 ... xn)T
E(v) = [E(x1) ... E(xn)]T
14. Co-variance of matrix Co-variance(v) of a random vector is the matrix of variances and Co-variance of component. If v = (x1 ... xn)T, the ijth component of the Co-variance(v) is sij
Properties
Starting from properties 1 to 7, c is a constant; x and y are random variables.
From given properties 8 to 12, w and v is random vector; b is a continuous vector; A is a continuous matrix.
8. E(v + w) = E(v) + E(w)
9. E(b) = b
10. E(Av) = A E(v)
11. Co-variance(v + b) = Co-variance(v)
12. Co-variance(Av) = A Co-variance(v) AT
Problem 1.
Let X be a random variable with PDF given by
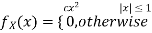
a, Find the constant c.
b. Find EX and Var (X).
c. Find P(X 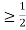 ).
).
Solution.
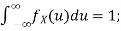
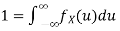
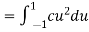
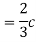
Thus we must have  .
.
b. To find EX we can write

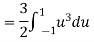
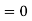
In fact, we could have guessed EX = 0 because the PDF is symmetric around x = 0. To find Var (X) we have
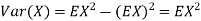
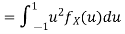
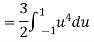
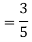
c. To find 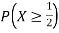 we can write
we can write

Problem 2. Let X be a continuous random variable with PDF given by
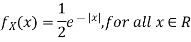
If  , find the CDF of Y.
, find the CDF of Y.
Solution. First we note that 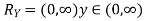 , we have
, we have
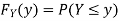
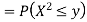
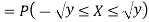
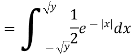
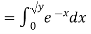

Thus, 
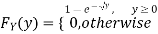
Problem 3. Let X be a continuous random variable with PDF
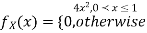
Find 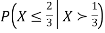 .
.
Solution. We have 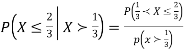
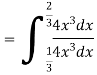
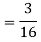
Probability Distribution:
A probability distribution is an arithmetical function which defines completely possible values &possibilities that a random variable can take in a given range. This range will be bounded between the minimum and maximum possible values. But exactly where the possible value is possible to be plotted on the probability distribution depends on a number of influences. These factors include the distribution's mean, SD, Skewness, and kurtosis.
Discrete Probability Distribution
Suppose a discrete variate X is the outcome of some experiment. If the probability that X takes the values 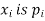 , then
, then
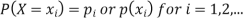
Where (i) 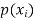
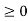 for all values of i, (ii)
for all values of i, (ii) 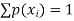
The set of values 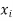 with their probabilities
with their probabilities 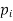 constitute a discrete probability distribution of the discrete variate X.
constitute a discrete probability distribution of the discrete variate X.
For example the discrete probability distribution for X the sum of the numbers which turns on tossing a pair of dice is given by the following table:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
Therefore there are 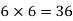 equally likely outcomes and therefore each has the probability 1/36. We have X = 2 for one outcome i.e. (1,1): X = 3 for two outcomes (1, 2) and (2, 1): X = 4 for three outcomes (1, 3), (2, 2) and (3, 1) and so on.
equally likely outcomes and therefore each has the probability 1/36. We have X = 2 for one outcome i.e. (1,1): X = 3 for two outcomes (1, 2) and (2, 1): X = 4 for three outcomes (1, 3), (2, 2) and (3, 1) and so on.
Distribution function. The distribution function F (x) of the discrete variate X is defined by
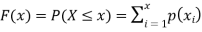 where x is any integer. The graph of F (x) will be stair step form (Fig.). The distribution function is also sometimes called cumulative distribution function.
where x is any integer. The graph of F (x) will be stair step form (Fig.). The distribution function is also sometimes called cumulative distribution function.
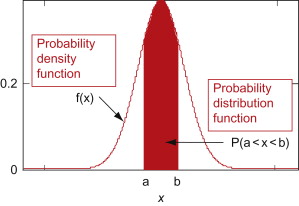
Probability Density:
Probability density function (PDF) is a arithmetical appearance which gives a probability distribution for a discrete random variable as opposite to a continuous random variable. The difference among a discrete random variable is that we check an exact value of the variable. Like, the value for the variable, a stock worth, only goes two decimal points outside the decimal (Example 32.22), while a continuous variable have an countless number of values (Example 32.22564879…).
When the PDF is graphically characterized, the area under the curve will show the interval in which the variable will decline. The total area in this interval of the graph equals the probability of a discrete random variable happening. More exactly, since the absolute prospect of a continuous random variable taking on any exact value is zero owing to the endless set of possible values existing, the value of a PDF can be used to determine the likelihood of a random variable dropping within a exact range of values.
Example. The probability density function of a variable X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P(X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
(i) Find 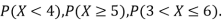
(ii) What will be e minimum value of k so that 
Solution. (i) If X is a random variable then


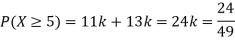


(ii)Thus minimum value of k=1/30.
Example. A random variate X has the following probability function
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P (x) | 0 | k | 2k | 2k | 3k |
|
|
|
(i) Find the value of the k.
(ii) 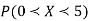
Solution. (i) If X is a random variable then
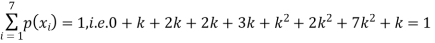
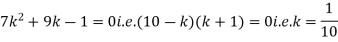
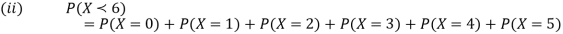

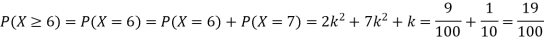
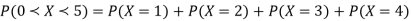

Continuous probability distribution
When a variate X takes every value in an interval it gives rise to continuous distribution of X. The distribution defined by the vidiots like heights or weights are continuous distributions.
A major conceptual difference however exist between discrete and continuous probabilities. When thinking in discrete terms the probability associated with an event is meaningful. With continuous events however where the number of events is infinitely large, the probability that a specific event will occur is practically zero. for this reason continuous probability statements on must be worth did some work differently from discrete ones. Instead of finding the probability that x equals some value, we find the probability of x falling in a small interval.
Thus the probability distribution of a continuous variate x is defined by a function f (x) such that the probability of the variate x falling in the small interval 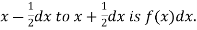 Symbolically it can be expressed as
Symbolically it can be expressed as 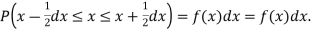 Thus f (x) is called the probability density function and then continuous curve y = f(x) is called the probability of curve.
Thus f (x) is called the probability density function and then continuous curve y = f(x) is called the probability of curve.
The range of the variable may be finite or infinite. But even when the range is finite, it is convenient to consider it as infinite by opposing the density function to be zero outside the given range. Thus if f (x) =(x) be the density function denoted for the variate x in the interval (a,b), then it can be written as
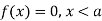
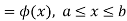
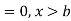
The density function f (x) is always positive and 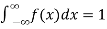 (i.e. the total area under the probability curve and the the x-axis is is unity which corresponds to the requirements that the total probability of happening of an event is unity).
(i.e. the total area under the probability curve and the the x-axis is is unity which corresponds to the requirements that the total probability of happening of an event is unity).
(2) Distribution function
If 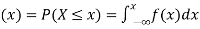
Then F(x) is defined as the commutative distribution function or simply the distribution function the continuous variate X. It is the probability that the value of the variate X will be ≤x. The graph of F(x) in this case is as shown in figure 26.3 (b).
The distribution function F (x) has the following properties
(i)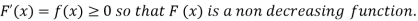
(ii)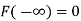
(iii)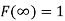
(iv)P(a ≤x ≤b)= 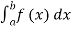 =
= 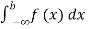 =F (b) – F (a).
=F (b) – F (a).
Example.
(i) Is the function defined as follows a density function.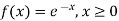
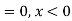
(ii) If so determine the probability that the variate having this density will fall in the interval (1.2).
(iii) Also find the cumulative probability function F (2)?
Solution. (i) f (x) is clearly ≥0 for every x in (1,2) and

Hence the function f (x) satisfies the requirements for a density function.
(ii)Required probability = 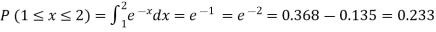
This probability is equal to the shaded area in figure 26.3 (a).
(iii)Cumulative probability function F(2)
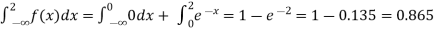
Which is shown in figure
Exponential Distribution:
The exponential distribution is a C.D. which is usually use to define to come time till some precise event happens. Like, the amount of time until a storm or other unsafe weather event occurs follows an exponential distribution law.
The one-parameter exponential distribution of the probability density function PDF is defined:
f(x)=λ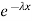 ,x≥0,
,x≥0,
where, the rate λ signifies the normal amount of events in single time.
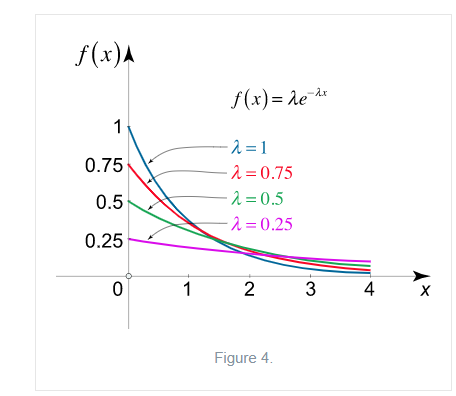
The mean value is μ=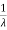 . The median of the exponential distribution is m=
. The median of the exponential distribution is m=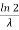 , and the variance is shown by
, and the variance is shown by 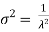 .
.
Normal Distribution:
Normal distribution
Now we consider continuous distribution of fundamental importance namely the normal distribution. Any quantity whose variation depends on random causes is distributed according to the normal law. its importance lies in the fact that a large number of distributions approximate to the normal distribution.
Latest define a variate 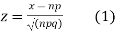
Where x no and S.D. 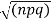 so that z is a very eighth with mean zero and variance unity. In the limit as n tends to infinity the distribution of z becomes a continuous distribution extending from
so that z is a very eighth with mean zero and variance unity. In the limit as n tends to infinity the distribution of z becomes a continuous distribution extending from 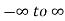 .
.
It can be shown that the limiting form of the binomial distribution (1) for large values of n when neither p nor q is very small is the normal distribution. The normal curve is of the form
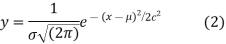
Where μ and  are the mean and standard deviation respectively..
are the mean and standard deviation respectively..
The normal distribution is the utmost broadly identified P.D. then it defines many usual spectacles.
The PDF of the normal distribution is shown by method
f(x)=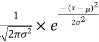 ,
,
where μ is mean of the distribution, and 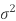 is the variance.
is the variance.
The 2 limitations μ and σ completely describe the figure and all additional things of the normal distribution function.

Example. X is a normal variate with mean 30 and S.D. 5, find the probabilities that
(i) 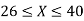
(ii) 
(iii) |X-30|≥5
Solution. We have μ =30 and 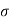 =5
=5
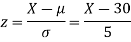
(i) When X = 26, z = -0.8, when X =40, z =-2
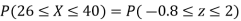
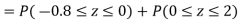
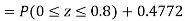
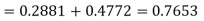
(ii) When X =45, z =3
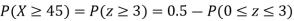

(iii) 
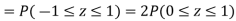
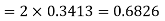
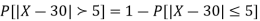

Example. In a normal distribution 31% of the items are under 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
Solution. Let 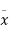 be the mean and
be the mean and  the standard deviation 31% of the items are under 45 means area to the left of the ordinate x = 45 (figure 26.6)
the standard deviation 31% of the items are under 45 means area to the left of the ordinate x = 45 (figure 26.6)
When x = 45, let z 
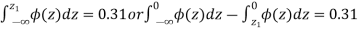
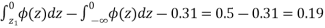
From table III 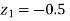
When x = 64, let  so that
so that 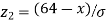
Hence, 
From table III 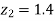
From (i) and (ii), 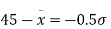
From (iii) and (iv), 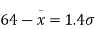
Solving these equations we get 
Example. In a test on 2000 electric bulbs, it was found that the life of a particular make was normally distributed with an average life of 2040 hours and standard deviation of 60 hours. Estimated number of bulbs likely to burn for
(a) More than 2150 hours
(b) Less than 1950 hours and
(c) More than 1920 hours and but less than 2 160 hours
Solution. Here μ = 2040 hours and 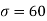 hours
hours
(a) For x = 2150, 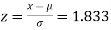
Area against z = 1.83 in the table III = 0.4664
We however require the area to the right of the ordinate at z = 1.83. This area = 0.5-0.4664=0.0336
Thus the number of bulbs expected to burn for more than 2150 hours.
= 0.0336×2000 = 67 approximately
(b) For x = 1950, 
The area required in this case is to be left of z = -1.33
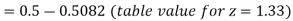
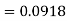
Therefore the number of bulbs expected to burn for less than 1950 hours
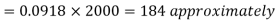
(c) When x = 1920, 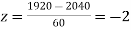
When x = 2160, 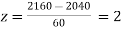
The number of bulbs expected to learn for more than 1920 hours but less than 2160 hours will be represented by the area between z = -2 and z = 2. This is twice the area from the table for z =2, i.e. 2 × 0.4772=0.9544
Thus required number of bulbs = 0.9544 × 2000 = 1909 nearly
Example. If the probability of committing an error of magnitude x is given by
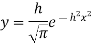
Compute the probable error from the following data:
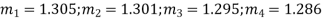
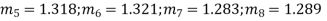

Solution. From the given data which is normally distributed, we have

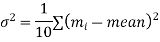


Gamma density
Consider the distribution of the sum of 2autonomous Exponential (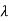 ) R.V.
) R.V.
Density of the form:
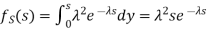
Density is known Gamma (2,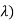 density. In common the gamma density is precise with 2 reasons (t,
density. In common the gamma density is precise with 2 reasons (t,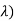 as being non zero on the +ve reals and called:
as being non zero on the +ve reals and called:
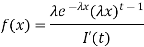
where F (t) is the endless which symbols integral of the density quantity to one:
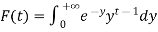
By integration by parts we presented the significant recurrence relative:
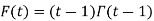
Because 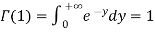 , we have for integer t=m
, we have for integer t=m
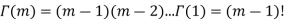
The specific case of the integer t can be linked to the sum of n independent exponential, it is the waiting time to the nth event, it is the matching of the negative binomial.
From that we can estimate what the estimated value and the variance are going to be: If all the Xi's are independent exponential (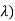 , then if we sum n of them we
, then if we sum n of them we
have 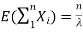 and if they are independent:
and if they are independent: 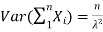
This simplifies to the non-integer t case:
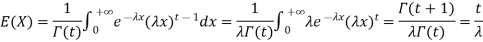
Example1: Following probability distribution
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P(x) | 0 |
|
|
|
|
|
|
|
Find: (i) k (ii) 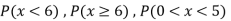
(i) Distribution function
(ii) If 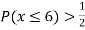 find minimum value of C
find minimum value of C
(iii) Find 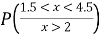
Solution:
If P(x) is p.m.f –
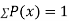
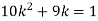
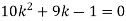
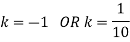
(i)
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P(x) | 0 |
|
|
|
|
|
|
|
(ii) 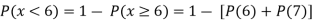
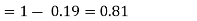
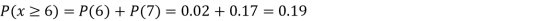
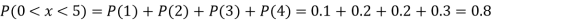
(iii)
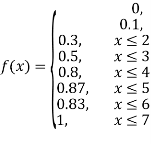
(iv)
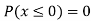
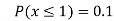

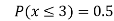
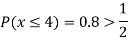
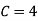
(v)
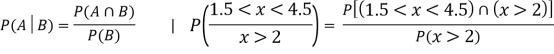
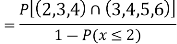
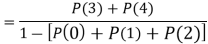
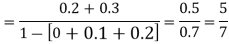
Example 2. I choose real number uniformly at random in the interval [a, b], and call it X. Buy uniformly at random, we mean all intervals in [a, b] that have the same length must have the same probability. Find the CDF of X.
Solution.
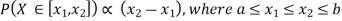
Since 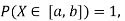 we conclude
we conclude
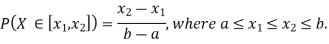
Now, let us find the CDF. By definition 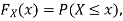 thus immediately have
thus immediately have
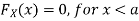
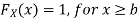
For 
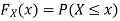
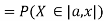
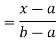
Thus, to summarize
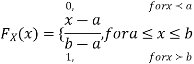
Note that hear it does not matter if we use “<” or “≤” as each individual point has probability zero, so for example 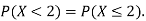 Figure 4.1 shows the CDF of X. As we expect the CDF starts at 0 at end at 1.
Figure 4.1 shows the CDF of X. As we expect the CDF starts at 0 at end at 1.
Example 3.
Find the mean value μ and the median m of the exponential distribution 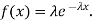
Solution. The mean value μ is determined by the integral
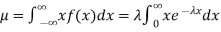
Integrating by parts we have
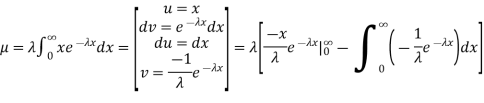
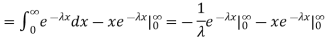
We evaluate the second term with the help of 1 Hopital's Rule:
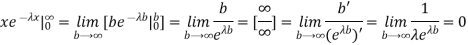
Hence the mean (average) value of the exponential distribution is
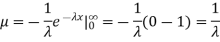
Determine the median m

A bivariate distribution, set only, is the probability that a definite event will happen when there are 2 independent random variables in your scenario. E.g, having two bowls, individually complete with 2dissimilarkinds of candies, and drawing one candy from each bowl gives you 2 independent random variables, the 2dissimilar candies. Since you are pulling one candy from each bowl at the same time, you have a bivariate distribution when calculating your probability of finish up with specific types of candies.
Properties:
Properties 1. Two random variables X and Y are said to be bivariate normal, or jointly normal distribution for all 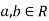
Properties 2:
Two random variables X and Y are set to have the standard bivariate normal distribution with correlation efficient if their joint PDF is given by
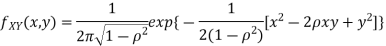
Where 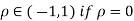 then we just say X and Y have the standard by will it normal distribution.
then we just say X and Y have the standard by will it normal distribution.
Properties 3:
Two random variables X and Y are set to have a bivariate normal distribution with parameters 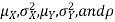 if their joint PDF is given by
if their joint PDF is given by
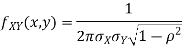
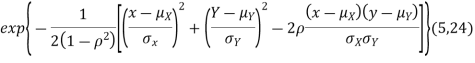
where 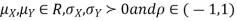 are all constants.
are all constants.
Properties 4:
Suppose X and Y are jointly normal random variables with parameters  . Then given X = x, Y is normally distributed with
. Then given X = x, Y is normally distributed with
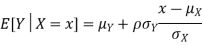
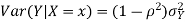
Example.
Let 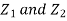 be two independent N (0, 1) random variables. Define
be two independent N (0, 1) random variables. Define
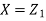
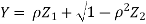
Where 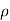 is a real number in (-1, 1).
is a real number in (-1, 1).

Solution.
First note that since 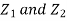 are normal and independent they are jointly normal with the joint PDF
are normal and independent they are jointly normal with the joint PDF
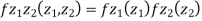
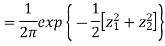
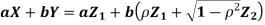

Which is the linear combination of  and thus it is normal.
and thus it is normal.
b. We can use the method of transformations (theorem 5.1) to find the joint PDF of X and Y. The inverse transformation is given by
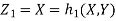
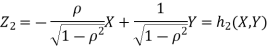
We have
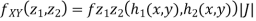
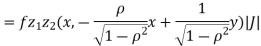
Where, 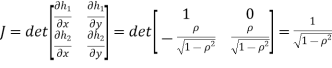
Thus we conclude that
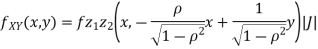

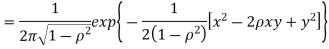
c. To find 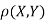 FIRST NOTE
FIRST NOTE
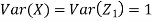
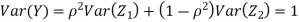
Therefore,
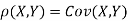
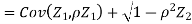
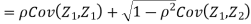
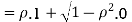
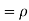
Example. Let X and Y be jointly normal random variable with parameters 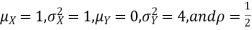


Solution.
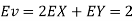
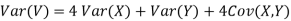
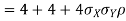
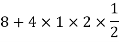
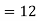
Thus V ~ N (2, 12). Therefore,
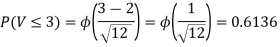
b. Note that Cov (X,Y)=  (X,Y) =1. We have
(X,Y) =1. We have

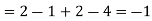
c. Using properties we conclude that given X =2, Y is normally distributed with
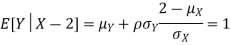

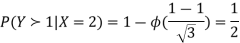
Given random variables X and Y that are defined on a probability space, the joint probability distribution for X and Y is a probability distribution that gives the probability that each of X and Y falls in any particular range or discrete set of values specified for that variable. In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to any number of random variables, giving a multivariate distribution.
The joint probability distribution can be expressed either in terms of a joint cumulative distribution function or in terms of a joint probability density function (in the case of continuous variables) or joint probability mass function (in the case of discrete variables). These in turn can be used to find two other types of distributions: the marginal distribution giving the probabilities for any one of the variables with no reference to any specific ranges of values for the other variables, and the conditional probability distribution giving the probabilities for any subset of the variables conditional on particular values of the remaining variables.
Example. A die is tossed thrice. A success is getting 1 or 6 on a toss. Find the mean and variance of the number of successes.
Solution. Probability of success 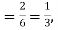 probability of failures
probability of failures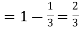
Probability of no success= probability of all three failures
Probability of one successes and two failures 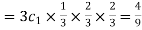
Probability of Two successes and one failure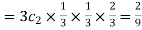
Probability of three successes 
| 1 | 2 | 3 |
| 4/9 | 2/9 | 1/27 |
Mean 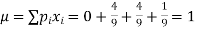
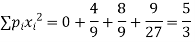
Variance,
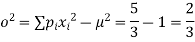
Example. The probability density function of a variate X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P (X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
Solution. (I) If X is random variable then

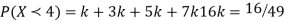
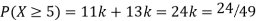

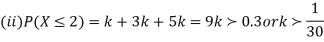
 hus minimum value of k =1/30
hus minimum value of k =1/30
Example. Random variable X has the following probability function
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P (x) | 0 | k | 2k | 2k | 3k |
|
|
|
(i) Find the value of the k
(ii) Evaluate P (X < 6), P (X≥6)
Solution. (i) if X is a random variable then
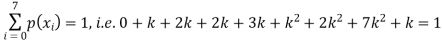
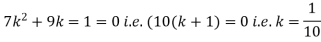
(ii)P (X < 6) =P( X=0) +P(X=1)+P(X=2)+ P(X=3) +P(X=4) + P (X=5)
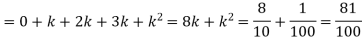
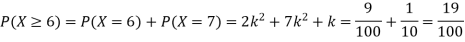
(iii) 

In probability theory assumed two jointly distributed R.V. X & Y. The conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a precise value; in some suitcases the conditional probabilities may be stated as functions containing the unnamedx value of X as a limitation. Once together X and Yare given variables, a conditional probability is characteristically used to indicate the conditional probability. The conditional distribution differences with the marginal distribution of a random variable, which is distribution deprived of reference to the value of the additional variable.
If conditional distribution of Y under X is a continuous distribution, then probability density function is called as conditional density function. The properties of a conditional distribution, such as the moments, are frequently denoted to by corresponding names such as the conditional mean and conditional variance.
Let A and B be two events of a sample space S and let 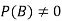 . Then conditional probability of the event A, given B, denoted by P (A/B) is defined by
. Then conditional probability of the event A, given B, denoted by P (A/B) is defined by
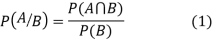
Theorem. If the events A and B defined on a sample space S of a random experiment are independent then
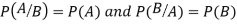
Proof. A and B are given to be independent events.
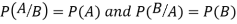
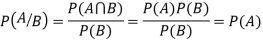
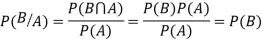
If 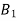 ,
, 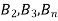 are mutually exclusive events with
are mutually exclusive events with 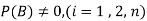 of a random experiment then for any arbitrary event
of a random experiment then for any arbitrary event 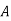 of the sample space of the above experiment with
of the sample space of the above experiment with 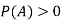 , we have
, we have
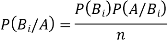
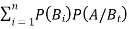 (for
(for 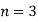 )
)

Example1: An urn 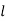 contains 3 white and 4 red balls and an urn lI contains 5 white and 6 red balls. One ball is drawn at random from one ofthe urns and isfound to be white. Find the probability that it was drawn from urn 1.
contains 3 white and 4 red balls and an urn lI contains 5 white and 6 red balls. One ball is drawn at random from one ofthe urns and isfound to be white. Find the probability that it was drawn from urn 1.
Solution: Let 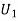 : the ball is drawn from urn I
: the ball is drawn from urn I
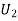 : the ball is drawn from urn II
: the ball is drawn from urn II
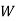 : the ball is white.
: the ball is white.
We have to find 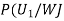
By Bayes Theorem
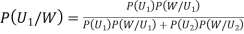 ... (1)
... (1)
Since two urns are equally likely to be selected, 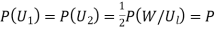 (a white ball is drawn from urn
(a white ball is drawn from urn  )
) 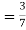
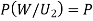 (a white ball is drawn from urn II)
(a white ball is drawn from urn II) 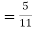
From(1), 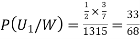
Example2: Three urns contains 6 red, 4 black, 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. lf the ball drawn is red find the probability that it is drawn from thefirst urn.
Solution: Let : the ball is drawn from urn 1.
: the ball is drawn from urn 1.
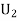 : the ball is drawn from urn lI.
: the ball is drawn from urn lI.
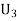 : the ball is drawn from urn 111.
: the ball is drawn from urn 111.
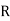 : the ball is red.
: the ball is red.
We have to find  .
.
By Baye’s Theorem,
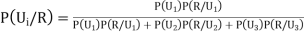 ... (1)
... (1)
Since the three urns are equally likely to be selected 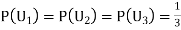
Also 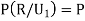 (a red ball is drawn from urn
(a red ball is drawn from urn 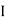 )
) 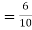
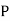 (R/
(R/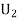 )
) 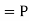 (a red ball is drawn from urn II)
(a red ball is drawn from urn II) 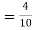
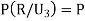 (a red ball is drawn from urn III)
(a red ball is drawn from urn III) 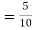
From (1), we have 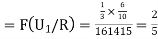
Example3: ln a bolt factory machines  and
and 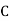 manufacturerespectively 25%, 35% and 40% of the total. lf their output 5, 4 and 2 per cent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B.
manufacturerespectively 25%, 35% and 40% of the total. lf their output 5, 4 and 2 per cent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B. ?
?
Solution: bolt is manufactured by machine 
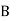 : bolt is manufactured by machine
: bolt is manufactured by machine 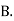
 : bolt is manufactured by machine
: bolt is manufactured by machine 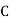
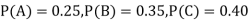
The probability ofdrawing a defective bolt manufactured by machine 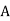 is
is 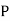 (D/A)
(D/A) 
Similarly, 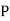 (D/B)
(D/B) 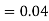 and
and 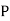 (D/C)
(D/C) 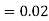
By Baye’s theorem
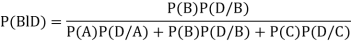
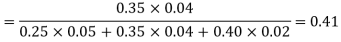
References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A text book of Engineering Mathematics, Laxmi Publications.
3. P. G. Hoel, S. C. Port and C. J. Stone, Introduction to Probability Theory, Universal Book Stall.
4. S. Ross, A First Course in Probability, 6th Ed., Pearson Education India,2002.