Unit – 10A
Biostatistics covering
Biostatistics is the science which deals with development and application of the most appropriate methods for the:
Therefore, when different statistical methods are applied in biological, medical and public health data they constitute the discipline of biostatistics.
Different characteristics that take different values in different persons, places and things, or the characteristics and properties, we wish to observe by members of a group (sample) which differ from one another are called “Variables” in statistics.
All the information regarding all the variables in the study is called data. There are two main types of data:
Although the types of variables could be broadly divided into categorical (qualitative) and numerical (quantitative), it has been a common practice to see four basic types of data (scales of measurement)
Both interval and ratio data involve measurement. Most data is techniques that apply to ratio data also apply to interval data. Therefore, in most practical aspects, these types of data (interval and ratio) are grouped under metric data.
Mean, median, and mode are the three measures of central tendencies.
Mean is the common measure of central tendency, most widely used in calculations of averages. It is least affected by sampling fluctuations. The mean of a number of individual values (X) is always nearer the true value of the individual value itself. Mean shows less variation than that of individual values, hence they give confidence in using them. It is calculated by adding up the individual values (Σx) and dividing the sum by number of items (n). Suppose height of 7 children's is 60, 70, 80, 90, 90, 100, and 110 cm. Addition of height of 7 children is 600 cm, so mean (X) = Σx/n = 600/7 = 85.71.
Median is an average, which is obtained by getting middle values of a set of data arranged or ordered from lowest to the highest (or vice versa). In this process, 50% of the population has the value smaller than and 50% of samples have the value larger than median. It is used for scores and ranks. Median is a better indicator of central value when one or more of the lowest or the highest observations are wide apart or are not evenly distributed. Median in case of even number of observations is taken arbitrary as an average of two middle values, and in case of odd number, the central value forms the median. In above example, median would be 90.
Mode is the most frequent value, or it is the point of maximum concentration. Most fashionable number, which occurred repeatedly, contributes mode in a distribution of quantitative data. In above example, mode is 90. Mode is used when the values are widely varying and is rarely used in medical studies.
For skewed distribution or samples where there is wide variation, mode, and median are useful. Even after calculating the mean, it is necessary to have some index of variability among the data. Range or the lowest and the highest values can be given, but this is not very useful if one of these extreme values is far off from the rest. At the same time, it does not tell how the observations are scattered around the mean. Therefore, following indices of variability play a key role in biostatistics.
Standard Deviation:
In addition to the mean, the degree of variability of responses has to be indicated since the same mean may be obtained from different sets of values. Standard deviation (SD) describes the variability of the observation about the mean. Todescribe the scatter of the population, most useful measure of variability is SD. Summary measures of variability of individuals (mean, median, and mode) are further needed to be tested for reliability of statistics based on samples from population variability of individual. To calculate the SD, we need its square called variance.
Variance is the average square deviation around the mean and is calculated by
Variance = Σ(x-x-) 2/n OR Σ(x-x-) 2/n-1, now SD = √variance.
SD helps us to predict how far the given value is away from the mean, and therefore, we can predict the coverage of values. SD is more appropriate only if data are normally distributed. If individual observations are clustered around sample mean (M) and are scattered evenly around it, the SD helps to calculate a range that will include a given percentage of observation. For example, if N ≥ 30, the range M ± 2(SD) will include 95% of observation and the range M ±3 (SD) will include 99% of observation. If observations are widely dispersed, central values are less representative of data, hence variance is taken. While reporting mean and SD, better way of representation is ‘mean (SD)’ rather than ‘mean ± SD’ to minimize confusion with confidence interval.
TYPES OF DISTRIBUTION
Though this universe is full of uncertainty and variability, a large set of experimental/biological observations always tend towards a normal distribution. This unique behavior of data is the key to entire inferential statistics. There are two types of distribution.
Gaussian /normal distribution: If data is symmetricallydistributed on both sides of mean and form a bell-shaped curve in frequency distribution plot, the distribution of data is called normal or Gaussian. The noted statistician professor Gauss developed this, and therefore, it was named after him. The normal curve describes the ideal distribution of continuous values i.e. heart rate, blood sugar level.
Whether our data is normally distributed or not, can be checked by putting our raw data of study directly into computer software and applying distribution test. Statistical treatment of data can generate a number of useful measurements, the most important of which are mean and standard deviation of mean. In an ideal Gaussian distribution, the values lying between the points 1 SD below and 1 SD above the mean value (i.e. ± 1 SD) will include 68.27% of all values. The range, mean ± 2 SD includes approximately 95% of values distributed about this mean, excluding 2.5% above and 2.5% below the range. In ideal distribution of thevalues: the mean, mode, and median are equal withinpopulation under study. Even if distribution in original population is far from normal, the distribution of sample averages tend to become normal as size of sample increases. This is the single most important reason for the curve of normal distribution. Various methods of analysis are available to make assumptions about normality, including ‘t’ test and analysis of variance (ANOVA). In normal distribution, skew is zero. If the difference (mean–median) is positive, the curve is positively skewed and if it is (mean–median) negative, the curve is negatively skewed, and therefore, measure of central tendency differs.
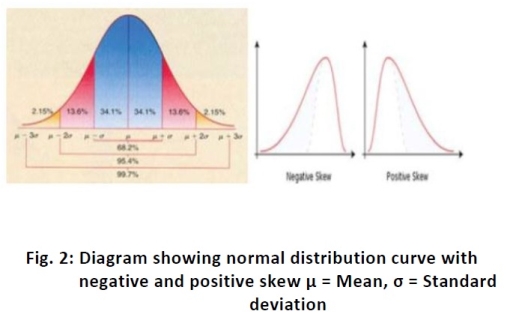
Non-Gaussian (non-normal) distribution: If the data is skewedon one side, then the distribution is non-normal. It may be binominal distribution or Poisson distribution. In binominal distribution, event can have only one of two possible outcomes such as yes/no, positive/negative, survival/death, and smokers/non-smokers.
Standard Error of Mean
Since we study some points or events (sample) to draw conclusions about all patients or population and use the samplemean (M) as an estimate of the population mean (M1), we need to know how far M can vary from M1 if repeated samples of size N are taken. A measure of this variability is provided by Standard error of mean (SEM), which is calculated as (SEM = SD/√n). SEM is always less than SD. What SD is to the sample, the SEM is to the population mean.
Null Hypothesis:
The primary object of statistical analysis is to find out whether the effect produced by a compound under study is genuine and is not due to chance. Hence, the analysis usually attaches a test of statistical significance. First step in such a test is to state the null hypothesis. In null hypothesis (statistical hypothesis), we make assumption that there exist no differences between the two groups. Alternative hypothesis (research hypothesis) states that there is a difference between two groups.
For example, a new drug ‘A’ is claimed to have analgesic activity and we want to test it with the placebo. In this study, the null hypothesis would be ‘drug A is not better than the placebo.’ Alternative hypothesis would be ‘there is a difference between new drug ‘A’ and placebo.’ When the null hypothesis is accepted, the difference between the two groups is not significant. It means, both samples were drawn from single population, and the difference obtained between two groups was due to chance. If alternative hypothesis is proved i.e. null hypothesis is rejected, then the difference between two groups is statistically significant. A difference between drug ‘A’ and placebo group, which would have arisen by chance is less than five percent of the cases, that is less than 1 in 20 times is considered as statistically significant (P < 0.05). In any experimental procedure, there is possibility of occurring two errors.
1) Type I Error (False positive)
This is also known as α error. It is the probability of finding a difference; when no such difference actually exists, which results in the acceptance of an inactive compound as an active compound. Such an error, which is not unusual, may be tolerated because in subsequent trials, the compound will reveal itself as inactive and thus finally rejected. For example, we proved in our trial that new drug ‘A’ has an analgesic action and accepted as an analgesic. If we commit type I error in this experiment, then subsequent trial on this compound will automatically reject our claim that drug ‘A’ is having analgesic action and later on drug ‘A’ will be thrown out of market. Type I error is actually fixed in advance by choice of the level of significance employed in test. It may be noted that type I error can be made small by changing the level of significance and by increasing the size of sample.
2) Type II Error (False negative)
This is also called as β error. It is the probability of inability to detect the difference when it actually exists, thus resulting in the rejection of an active compound as an inactive. This error is more serious than type I error because once we labelled the compound as inactive, there is possibility that nobody will try it again. Thus, an active compound will be lost. This type of error can be minimized by taking larger sample and by employing sufficient dose of the compound under trial. For example, we claim that drug ‘A’ is not having analgesic activity after suitable trial. Therefore, drug ‘A’ will not be tried by any other researcher for its analgesic activity and thus drug ‘A’, in spite of having analgesic activity, will be lost just because of our type II error. Hence, researcher should be very careful while reporting type II error.
How to Choose an Appropriate Statistical Test
There are number of tests in biostatistics, but choice mainly depends on characteristics and type of analysis of data. Sometimes, we need to find out the difference between means or medians or association between the variables. Number of groups used in a study may vary; therefore, study design also varies. Hence, in such situation, we will have to make the decision which is more precise while selecting the appropriate test. In appropriate test will lead to invalid conclusions. Statistical tests can be divided into parametric and non- parametric tests. If variables follow normal distribution, data can be subjected to parametric test, and for non- Gaussian distribution, we should apply non-parametric test. Statistical test should be decided at the start of the study.
Following are the different parametric test used in analysis of various types of data.
1) Student's ‘t’ Test
Mr. W. S. Gosset, a civil service statistician, introduced‘t’ distribution of small samples and published his work under the pseudonym ‘Student.’ This is one of the most widely used tests in pharmacological investigations, involving the use of small samples. The‘t’ test is always applied for analysis when the number of sample is 30 or less. It is usually applicable for graded data like blood sugar level, body weight, height etc. If sample size is more than 30, ‘Z’ test is applied. There are two types of ‘t’ test, paired and unpaired.
When to apply paired and unpaired
a) When comparison has to be made between two measurements in the same subjects after two consecutive treatments, paired ‘t’ test is used. For example, when we want to compare effect of drug A (i.e. decrease blood sugar) before start of treatment (baseline) and after 1 month of treatment with drug A.
b) When comparison is made between two measurements in two different groups, unpaired ‘t’ test is used. For example, when we compare the effects of drug A and B (i.e. mean change in blood sugar) after one month from baseline in both groups, unpaired ‘t’ test’ is applicable.
2) ANOVA
When we want to compare two sets of unpaired or paired data, the student’s‘t’ test is applied. However, when there are 3 or more sets of data to analyze, we need the help of well-designed and multi-talented method called as analysis of variance (ANOVA). This test compares multiple groups at one time. In ANOVA, we draw assumption that each sample is randomly drawn from the normal population, and also they have same variance as that of population. There are two types of ANOVA.
A) One way ANOVA: It compares three or more unmatchedgroups when the data are categorized in one way. For example, we may compare a control group with three different doses of aspirin in rats. Here, there are four unmatched group of rats. Therefore, we should apply one way ANOVA. We should choose repeated measures ANOVA test when the trial uses matched subjects. For example, effect of supplementation of vitamin C in each subject before, during, and after the treatment. Matching should not be based on the variable you are com paring. For example, if you are comparing blood pressures in two groups, it is better to match based on age or other variables, but it should not be to match based on blood pressure. The term repeated measures applies strictly when you give treatments repeatedly to one subjects. ANOVA works well even if the distribution is only approximately Gaussian. Therefore, these tests are used routinely in many field of science. The P value is calculated from the ANOVA table.
B) Two ways ANOVA: Also called two factors ANOVA, determineshow a response is affected by two factors. For example, you might measure a response to three different drugs in both men and women. This is a complicated test. Therefore, we think that for postgraduates, this test may not be so useful.
Importance of post hoc test
Post tests are the modification of‘t’ test. They account for multiple comparisons, as well as for the fact that the comparison are interrelated. ANOVA only directs whether there is significant difference between the various groups or not. If the results aresignificant, ANOVA does not tell us at what point the difference between various groups subsist. But, post test is capable to pinpoint the exact difference between the different groups of comparison. Therefore, post tests are very useful as far as statistics is concerned. There are five types of post- hoc test namely; Dunnett's, Turkey, Newman-Keuls, Bonferroni, and test for linear trend between mean and column number.
Following are the non-parametric tests used for analysis of different types of data.
1) Chi-square test
The Chi-square test is a non-parametric test of proportions. This test is not based on any assumption or distribution of any variable. This test, though different, follows a specific distribution known as Chi-square distribution, which is very useful in research. It is most commonly used when data are in frequencies such as number of responses in two or more categories. This test involves the calculations of a quantity called Chi-square (x2) from Greek letter ‘Chi’(x) and pronounced as ‘Kye.’ It was developed by Karl Pearson.
Applications
a) Test of proportion: This test is used to find the significance of difference in two or more than two proportions.
b) Test of association: The test of association between two events in binomial or multinomial samples is the most important application of the test in statistical methods. It measures the probabilities of association between two discrete attributes. Two events can often be studied for their association such as smoking and cancer, treatment and outcome of disease, level of cholesterol and coronary heart disease. In these cases, there are two possibilities, either they influence or affect each other or they do not. In other words, you can say that they are dependent or independent of each other. Thus, the test measures the probability (P) or relative frequency of association due to chance and also if two events are associated or dependent on each other. Varieties used are generally dichotomous e.g. improved / not improved. If data are not in that format, investigator can transform data into dichotomous data by specifying above and below limit. Multinomial sample is also useful to find out association between two discrete attributes. For example, to test the association between numbers of cigarettes equal to 10, 11-20, 21-30, and more than 30 smoked per day and the incidence of lung cancer. Since, the table presents joint occurrence of two sets of events, the treatment and outcome of disease, it is called contingency table (Con- together, tangle- to touch).
2) Wilcoxon-Matched-Pairs Signed-Ranks Test
This is a non-parametric test. This test is used when data are not normally distributed in a paired design. It is also called Wilcoxon-Matched Pair test. It analyses only the difference between the paired measurements for each subject. If P value is small, we can reject the idea that the difference is coincidence and conclude that the populations have different medians.
3) Mann-Whitney test
It is a Student’s‘t’ test performed on ranks. For large numbers, it is almost as sensitive as Student’s‘t’ test. For small numbers with unknown distribution, this test is more sensitive than Student’s‘t’ test. This test is generally used when two unpaired groups are to be compared and the scale is ordinal (i.e. ranks and scores), which are not normally distributed.
4) Friedman test
This is a non-parametric test, which compares three or more paired groups. In this, we have to rank the values in each row from low to high. The goal of using a matched test is to control experimental variability between subjects, thus increasing the power of the test.
5) Kruskal-Wallis test
It is a non-parametric test, which compares three or more unpaired groups. Non-parametric tests are less powerful than parametric tests. Generally, P values tend to be higher, making it harder to detect real differences. Therefore, first of all, try to transform the data. Sometimes, simple transformation will convert non-Gaussian data to a Gaussian distribution. Non-parametric test is considered only if outcome variable is in rank or scale with only a few categories. In this case, population is far from Gaussian or one or few values are off scale, too high, or too low to measure.
References:
1. Žiga Turk (2014), Global Challenges and the Role of Civil Engineering, Chapter 3 in: Fischinger M. (eds) Performance-Based Seismic Engineering: Vision for an Earthquake Resilient Society. Geotechnical, Geological and Earthquake Engineering, Vol. 32. Springer, Dordrecht
2. Brito, Ciampi, Vasconcelos, Amarol, Barros (2013) Engineering impacting Social, Economical and Working Environment, 120th ASEE Annual Conference and Exposition
3. NAE Grand Challenges for Engineering (2006), Engineering for the Developing World, The Bridge, Vol 34, No.2, Summer 2004.
4. Allen M. (2008) Cleansing the city. Ohio University Press. Athens Ohio.
5. Ashley R., Stovin V., Moore S., Hurley L., Lewis L., Saul A. (2010). London Tideway Tunnels Programme – Thames Tunnel Project Needs Report – Potential source control and SUDS applications: Land use and retrofit options
6. Ashley R M., Nowell R., Gersonius B., Walker L. (2011). Surface Water Management and Urban Green Infrastructure. Review of Current Knowledge. Foundation for Water Research FR/R0014
7. Barry M. (2003) Corporate social responsibility – unworkable paradox or sustainable paradigm? Proc ICE Engineering Sustainability 156. Sept Issue ES3 paper 13550. p 129-130
8. Blackmore J M., Plant R A J. (2008). Risk and resilience to enhance sustainability with application to urban water systems. J. Water Resources Planning and Management. ASCE. Vol. 134, No. 3, May.
9. Bogle D. (2010) UK’s engineering Council guidance on sustainability. Proc ICE Engineering Sustainability 163. June Issue ES2 p61-63
10. Brown R R., Ashley R M., Farrelly M. (2011). Political and Professional Agency Entrapment: An Agenda for Urban Water Research. Water Resources Management. Vol. 23, No.4. European Water Resources Association (EWRA) ISSN 0920-4741.
11. Brugnach M., Dewulf A., Pahl-Wostl C., Taillieu T. (2008) Toward a relational concept of uncertainty: about knowing too little, knowing too differently and accepting not to know. Ecology and Society 13 (2): 30
12. Butler D., Davies J. (2011). Urban Drainage. Spon. 3rd Ed.
13. Cavill S., Sohail M. (2003) Accountability in the provision of urban services. Proc. ICE. Municipal Engineer 156. Issue ME4 paper 13445, p235-244.
14. Charles J A. (2009) Robert Rawlinson and the UK public health revolution. Proc ICE Eng History and Heritage. 162 Nov. Issue EH4. p 199-206