Unit - 5
Laminar Flow
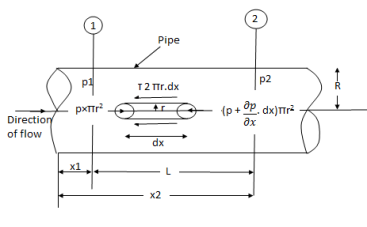
Fig no 1 Circular pipes
Fig: Shows a horizontal circular pipe of radius R, having laminar flow of fluid through it.
Consider a small concentric cylinder of radius r and length dx as a free body.
If  is the shear stress, the shear force F is given by
is the shear stress, the shear force F is given by
F =  x 2
x 2  r x dx
r x dx
Let P be the intensity of pressure at left end and the intensity of pressure at the right end be (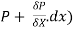
Thus, the force acting on the fluid element are:
The shear force,  x 2
x 2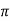 r x dx on the surface of fluid element.
r x dx on the surface of fluid element.
The pressure force, P x 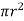 on the left end.
on the left end.
The pressure force, (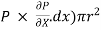 on the right end.
on the right end.
For steady flow, the net force on the cylinder must be zero.
 [ p x
[ p x 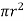 - (
- (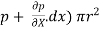 ] –
] – 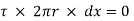
 -
- 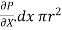 -
-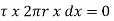
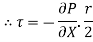
Shear stress is zero at the centre of pipe (r = 0) and maximum at the pipe wall given by
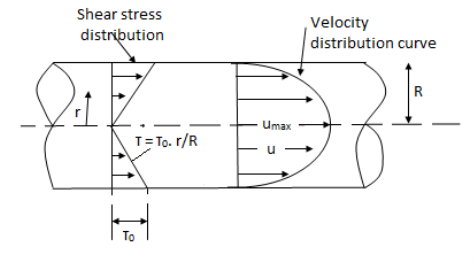
Fig no 2 When shear stress is zero
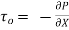 (
( )
)
From Newton’s Law of viscosity
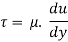
In this equation, the distance y is measured from the boundary. The radial distance r is related to distance y by the relation.
y = R-r ordinate y = -d r
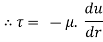
Comparing two values of 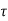
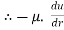 =
= 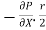
 du =
du = 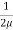 (
(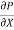 )r.dr
)r.dr
Integrating the above equation w. r. t. ‘r’ we get
 u =
u = 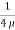 .
. 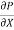 r2 + C --------------- (ii)
r2 + C --------------- (ii)
Where C is the constant of integration and its value is obtained from the boundary conditions.
At r = R, u = 0
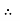 0 =
0 = 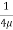 .
.  R2 + C or C =
R2 + C or C =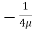 .
. 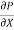 R2
R2
Substituting this value of C in eqn. (ii) we get,
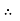 u =
u = 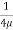 .
. 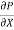 r2
r2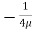 .
. 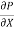 R2
R2
 u = -
u = - 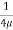 .
. 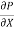 (R2 – r2)
(R2 – r2)
Shows that velocity distribution curve is a parabola.
The maximum velocity occurs, at the centre and is given by.
 umax = -
umax = - 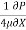 R2
R2
Examples:
Q.1 Show that for a steady laminar flow through a circular pipe mean velocity of flow occurs at a radial distance of 0.707R from the centre of pipe where R is radius of pipe.
Soln.:
Velocity distribution in laminar flow
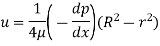
Average velocity ü
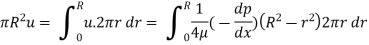
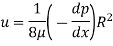
Radius at u= u. put in Equation (1)
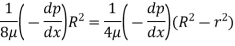
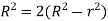
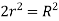
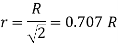
Q.2 An oil of viscosity 15 poise flows through a pipe of diameter 150 mm at a velocity of 2.5 m/s. If the specific gravity of oil is 0.9, find:
(1) Pressure gradient in direction of flow
(2) Share stress at the wall of pipe
(3) Reynolds number of flow of oil.
(4) Velocity at a distance of 50 mm from wall.
Soln.:
Given:
Viscosity = 15 poise = 1.5 N s/m²,
Diameter D = 150 mm= 0.15 m
Velocity 13 m/s,
Specific gravity, 0.9
To find
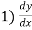 2)
2)  3) Re 4) Vat r = 0.05 m
3) Re 4) Vat r = 0.05 m
Radius of pipe R
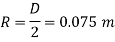
Pressure gradient in the direction of flow
Using relation
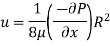
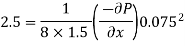
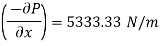
(2) Shear stress at the wall of pipe,
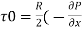 )
)
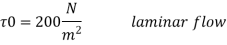
3] Reynolds’s number
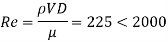
Laminar flow
(4) Velocity at a distance of 50 mm from wall

Q.3 A laminar flow is taking place in a pipe of diameter 0.2m. The maximum velocity is 1.5m/s. Find the mean velocity and the radius at which this occurs also calculate the velocity at 0.04m from the wall of the pipe.
Soln.
Given:
D= 0.2 m
Umax= 1.5 m/s
Y= 0.04 m
Radius of pipe R=-0.1 m
Mean velocity u= Umax/2 = 0.75 m/s
Velocity at 0.04 m from pipe wall
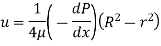
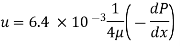
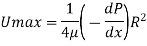
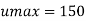
Put the value 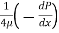
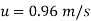
The Velocity at y = 0.04 m is 0.96 m/s
Q.4 Heated compound in the plastic state is forced through the die is an injection molding process under a pressure of 1 MPa. The diameter and length of the die being 8 mm and 3 m long respectively. If the mean velocity of flow is 0.48 m/s, calculate the viscosity of the plastic compound the heated state. Assume laminar flow
Soln.:
Given:
P1-P2 = 1 Mpa= 1x10^6 N/m^2
D= 8 mm= 0.008 m.
L= 3 m
u = 0.48 m/sec
To find:

The viscosity of plastic compound is 1.388 Nam.
Q.5 An oil of density 917 kg/m' is being pumped in a 15 cm diameter pipe. The discharge is measured as 850 L/min. The drop in pressure in a stretch of 800 m of pipeline, both ends of which are at the same elevation, is measured as 95 kPa. Estimate the absolute viscosity of the oil.
Soln.:
Given:
P1-p2 = 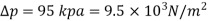
D= 15 cm = 0.15 m
L= 800 m
Q= 850 lit/min = 0.0142 m2/sec
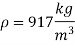
Find: Absolute viscosity
Average velocity
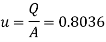
Using relation of pressure difference
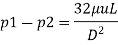
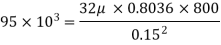
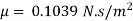
The absolute Viscosity is 0.1039 N.s/m^2
Q.6 An oil having a viscosity of 10 poise flows through a pipe of 500 mm diameter at a rate of 500 lit per second. Find the type of flow occurring in the pipe, if the specific gravity of all is 0.9.
Soln.:
Given
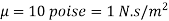
D= 500 mm = 0.5 m
Q= 500 Liter per second-0.5 m/sec,
S=0.9
To find: Type of fluid
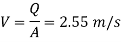
Reynolds number
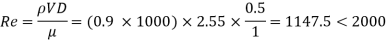
The flow is laminar.
Q. 7 What power will be required per km length of pipe line to overcome viscous resistance to flow of crude oil of viscous 1.9 poise through a horizontal pipe of 10 cm diameter at the rate of 650 liters per hour? Take specific gravity of oil = 0.85.
Soln.:
Given:
L.= 1000 m.
 = 1.9 poise = 0.19 N.s/m²
= 1.9 poise = 0.19 N.s/m²
D=10 cm=0.1 m
Q=650 liter/hour = 1.806x10^-4 m^3/sec
S = 0.85
Average velocity

To find:
P Pressure head,
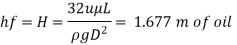
Power
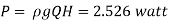
Power required to overcome viscous resistance is 2.526
Q. 8 Crude oil R.D. 0.9 is pumped through a smooth horizontal oil is 2.5 stokes. Differential pressure head between two ends of the pipe is 16.31 m of oil. Assuming the flow of oil is to be laminar, Find:
(1) Rate of flow of oil through pipe.
(2) Power required maintaining the flow.
Also check whether the flow is actually laminar or not pipe 400 m long. 100 mm diameter, kinematics viscosity of
Soln.:
Given:
RD= 0.9
L= 400 m
D= 100 mm= 0.1 m
V= 2.5 stokes
Density of oil, p=S x P=0.9x1000= 900 kg/m
Dynamic viscosity, u=p v=900x25x10 =0 225 N-x/m
Average velocity by Hagen Poiseuille's formula,
.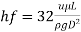

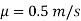
Discharge, Q=ū× A = 0.5 × x 0.1² = 3.927 x 10³ m³/sec
Power, P = pg HQ
= 900×9.81×16.31 x 3.927x10-³
= 565.49 watt
Power required maintaining the flow is 565.49 watt. or How, 2000
Reynolds’s number for given flow is,
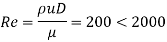
The actual flow is laminar
Key takeaways:
Velocity through circular pipes
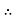 u = -
u = - 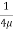 .
. 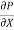 (R2 – r2)
(R2 – r2)
Maximum velocity
 umax = -
umax = - 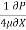 R2
R2
1. Flow of viscous fluid between two parallel plates when one plate is moving & other of Rest – Coutts flow
Consider laminar flow between two parallel flat plates located at a distance b apart such that lower plate is at rest & the upper plates moves uniformly with a constant velocity U as shown in fig.
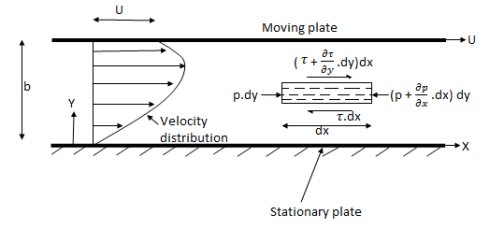
Fig no 3 Parallel plates
A small rectangular element of fluid of length dx, thickness dy& unit width is
Considered as a free body.
The forces acting on the fluid element are
1) The pressure force p dy x 1 on left end
2) The pressure force (p +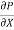 . d x) d y x1 on the right end.
. d x) d y x1 on the right end.
3) The shear force 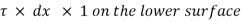
4) The shear force [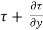 . dy] dx x 1 on the surface.
. dy] dx x 1 on the surface.
For steady & uniform flow the resultant force in the direction of flow is zero.
p. dy – (p + 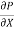 . dx) dy –
. dx) dy – 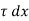 + (
+ ( +
+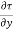 . dy) dx = 0
. dy) dx = 0
-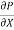 dx. dy +
dx. dy + 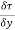 dy. dx = 0
dy. dx = 0
Dividing by the volume of element dx dy we get
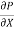 =
= 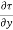 ------------------- (1)
------------------- (1)
Above equation shows the interdependence of shear & pressure gradients
According to Newton’s law of viscosity for laminar flow the shear stress
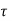 =
= 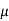 .
. 
Put in equation (1) we get,
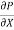 =
= 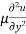
Integrating above equation twine w.r.t. y
u = 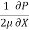 y2 + C1 y + C2 ------------- (2)
y2 + C1 y + C2 ------------- (2)
At y = 0, u = 0 & at y = b, u = U
We get C2 = 0 & C1 = 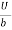 -
- 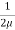 (
(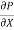 ) b
) b
Put values of C1& C2 in eqn. (2)
u = 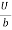 y -
y - 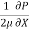 (by – y2)
(by – y2)
q = 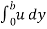 =
= 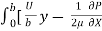 (by – y2)] dy
(by – y2)] dy
U. 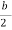 -
- 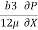
The distribution of shear stress across any section may be determined by using
Newton’s Law of viscosity
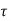 = u.
= u. 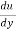 =
=  [
[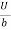 -
- 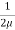 (
(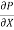 ) (b – 2y)]
) (b – 2y)]
= 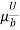 -
- 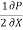 (b – 2y)
(b – 2y)
Both Plates at Rest:
In this case the equations for velocity, discharge q and the shear can be obtained from similar equation for generalizes Coutts flow by putting U = 0
Thus, for flow between two stationary parallel plates
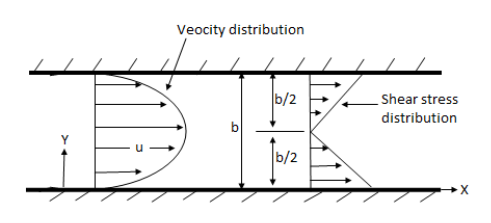
Fig no 4 Both pates are in parallel
u = - 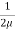 .
. 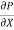 (by – y2)
(by – y2)
Discharge per unit width,
q = 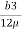 .
. 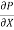
Shear stress 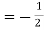 .
. 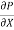 (b –2y)
(b –2y)
Examples:
Q.1 Two horizontal plates kept at 100 mm apart have laminar flow of oil of viscosity 1.5 N.s/m between them. The maximum velocity of flow is 2 m/s. Find:
(1) Discharge per meter width
(2) Shear stress at the plate
(3) Velocity gradient at the plate
(4) Pressure difference between two points 15 m apart.
Soln.:
Given: t = 100 mm = 0.1 m, U = 2 m/s, μ = 5 N-s/m², L=15m, b=1m
(i) Relation between ū and Umax,

(ii) Discharge per meter width,
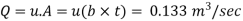
Pressure gradient use Equation
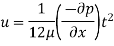
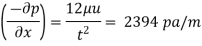
Shear stress at the plate,
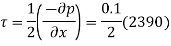
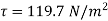
(iii) Pressure difference between two points

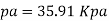
(iv) Velocity gradient of plates,
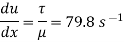
Q. 2 Two parallel plates kept 20 mm apart have laminar flow of oil between them maximum velocity of 2 m/s. Calculate:
(1) Discharge per meter width
(i) Shear stress at the plate
(iii) The difference in pressure between two points 20 m apart
(iv) Velocity gradient of plates
(v) Velocity at 0.02 mm from the plate. Assume viscosity of oil = 2.453 N-s/m Dec. 2004, 10 Marks
Soln.:
Given:
t = 20 mm = 0.2 m. Um=2 m/sc, = 2.453 N-s/m²,
L = 20 m, b= 1 m
(iii) Relation between ū and Umax,

(iv) Discharge per meter width,
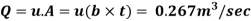
Pressure gradient use Equation
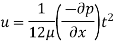
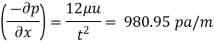
Shear stress at the plate,

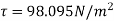
(iii) Pressure difference between two points
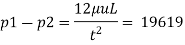
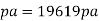
(iv) Velocity gradient of plates,
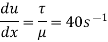
(v) Velocity at any point,
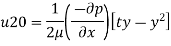
y-20 mm = 0.02


Velocity at 20 mm from plate 0.7198 m/sec
Q.3 Oil of relative density 0.92 and dynamic viscosity 1.05 poise flowing between two parallel fixed plates, 12 mm apart, has mean velocity of 1.4 m/s. Calculate:
1) The maximum velocity
2) The boundary shear stress
3) Velocity and shear stress at a distance of 2 mm from one of the plate
4) Loss of head over a distance 25 m. Dec. 2012, 10 Marks
Soln.:
Given: R.D=0.92. = 1.05 poise = 0.105 Pa-s
t = 12mm=0.012=14m
1) Maximum velocity.
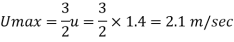
2) Boundary shear stress
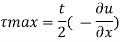
Now for pressure gradient, use Equation

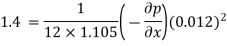
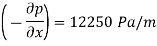

3) a) Velocity at a distance 2 mm from plate, use Equation
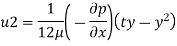
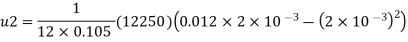
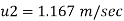
b) Shear stress at y = 2 mm
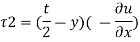

4) Loss of head over a distance 25 m
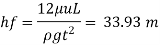
Q.4 Glycerin of specific gravity of 1.28 and viscosity 8.07 poise flows between two large parallel plates kept 1.5 cm apart The rate of flow is 4.4 m per hour meter width of plates. Determine the maximum velocity, maximum shear strops, pressure gradient and Reynolds number...
Soln.:
Given:
S= 1.28
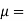 8.07 poise = 0.807 N-s/m',
8.07 poise = 0.807 N-s/m',
t= 1.5 cm-0.015 m
Q=- 4.4 m per hour per meter width of plate
Discharge per meter width= mean velocity. Area
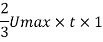
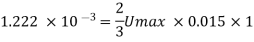
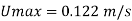
Pressure gradient,
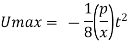
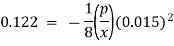
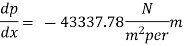
Maximum shear stress
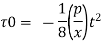
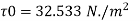
Reynolds Number
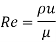
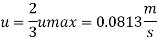
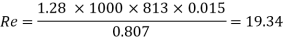
Q.5 Two parallel plates are kept 3 mm apart. For a steady laminar flow of oil between these plates, there was a pressure drop of 10 kN/m² per meter length of plates. If the viscosity of the oil is 5 x 10 N-s/m, determine the discharge per meter width of plates, maximum shear and maximum velocity of flow.
Soln.:
Given
t = 3 mm = 3x10 m.
p1, -p2 = 10 kN/m²
L = 1m,
 5x10¹ N./m²
5x10¹ N./m²
Drop of pressure in a length of 1 m, use equation
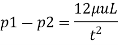

Discharge per meter width,
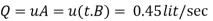
Maximum shear stress,
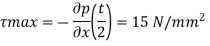
Maximum velocity,
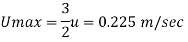
Q.6 A masonry wall of a water tank is 0.9 m thick. At the bottom a crack of thickness 0.3 mm and 600 mm wide has developed and the crack extends to the entire thickness of the wall. If the tank contains 4 m of water above the crack and the other crack is at atmospheric pressure, estimate the leakage volume per day from the crack. Kinematic viscosity of water = 0.01 stokes.
Soln.:
Given:
L= 0.9 m, t=0.3 mm = 3 x 10 m.
Width, b= 600 mm = 0.6 m h, H = 4 m of water above crack.
v=0.01 stokes = 1 x 10 m²/sec
Dynamic viscosity,
μ = p. v = 1000x1x10* = 0.001 N-s/m²
Using drop of pressure head formula,
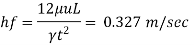
Rate of flow
Q = Au= (width x thickness) u
= (0.6×3×10) x 0.327 = 5.886 x 10³ m³/sec
Leakage volume per day,
Q  3600C24 = 5.886 x 10³ x 3600x24
3600C24 = 5.886 x 10³ x 3600x24
= 5.085 m²/day
Leakage from crack is 5.085 m'/day.
Key takeaways:
The distribution of shear stress across any section may be determined by using
Newton’s Law of viscosity
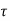 = u.
= u. 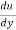 =
= 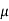 [
[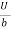 -
- 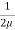 (
(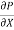 ) (b – 2y)]
) (b – 2y)]
= 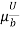 -
- 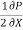 (b – 2y)
(b – 2y)
Plates in rest
Discharge per unit width,
q =  .
. 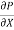
Shear stress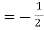 .
.  (b –2y)
(b –2y)
The strength of the viscosity in a small area conveying viscous fluid is provided by:
Fd = 6 pi u R v
Where:
Fd is the force of friction - known as Stokes' drag - which operates on a visible link between liquid and particles
μ is strong viscosity (some authors use the symbol η)
R is the radius of the circular object
v is the velocity of the flow relative to an object.
Laminar Flow
Round particles
Similar (made in the same way)
Smooth surfaces
The particles do not interfere with each other.
Applications
Terminal velocity of speed falling in a fluid
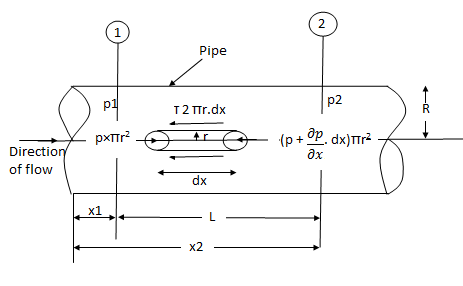
Fig no 5 Terminal velocity of speed falling in a fluid
F g =( ρ p - ρ f ) g 4/ 3 pi R3
V = 2/ 9 ( ρ p - ρ f ) / μ g R2
Where
g field gravitational force (m / s2)
R is the radius of circular particles (m)
ρ p particle size (kg / m3)
ρf maximum water weight (kg / m3)
μ is the strong viscosity (kg / (m * s)).
Key takeaways:
The strength of the viscosity in a small area conveying viscous fluid is provided by:
Fd = 6 pi u R v
Where:
Fd is the force of friction - known as Stokes' drag - which operates on a visible link between liquid and particles
μ is strong viscosity (some authors use the symbol η)
R is the radius of the circular object
v is the velocity of the flow relative to an object.
1. Rotating cylinder method
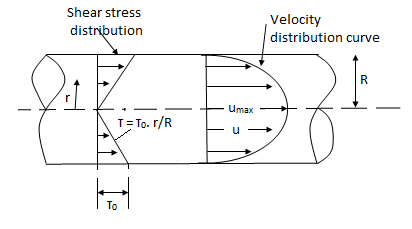
Fig no 6 Rotating cylinder viscometer
According to Newton’s law of viscosity,
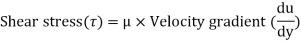
Since the annular space t = (R2 – R1) is quite small (where R2 and R1 are the radii of the outer and inner cylinders respectively), the velocity gradient
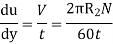
(Where N= the rotational speed of the outer cylinder in rpm)
Shear stress =
= 
Viscous drag = Shear stress × Area
= 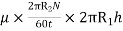
(Where h = height of liquid)
Viscous torque = Viscous drag x radius
=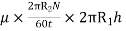 x
x 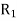
Viscous torque must be equal to the torque T exerted by the torquemeter.
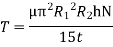
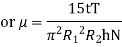
Thus, a rotational type viscometer can be calibrated to directly give u for given speed of rotation N.
2. Falling Sphere Method
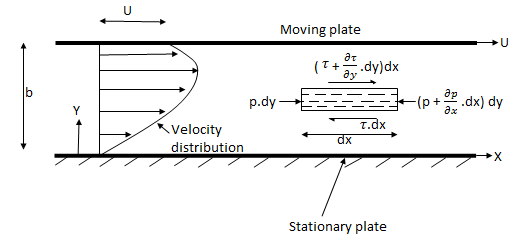
Fig no 7 Falling sphere viscometer
d = Diameter of the spherical ball.
l = distance travelled by the sphere in viscous liquid.
t = Time taken by the sphere to cover distance l
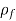 = Density of sphere
= Density of sphere
 = Density of fluid/liquid
= Density of fluid/liquid
W = weight of sphere
FB = Buoyant force acting on the sphere
FD = Drag force, and
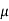 = Dynamic viscosity of the liquid under test.
= Dynamic viscosity of the liquid under test.
The force acting on the sphere are-
1) Weight W, acting vertically downward.
2) Buoyant force FB, acting vertically upward
3) Drag force FD, acting vertically upward.
W= volume × Density of sphere × g
=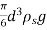
FB = weight of liquid displaced
= volume of liquid displaced × density of liquid × g
=
FD = 3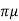 VD
VD
For equilibrium
FD + FB = W
FD = W – FB
3 VD =
VD = 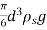 -
- 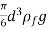 =
= 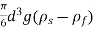
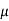 =
= 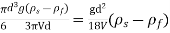
From the above equation the value of dynamic viscosity u can be determined.
3. Redwood viscometer

Fig no 8 Redwood viscometer
Examples:
Q. 1 A small air bubble of diameter 1 mm rises with a steady state velocity of 1.5 cm/sec through an oil. Estimate the viscosity of the oil if its specific gravity is 0.9.
Soln.:
Given:
d=1 mm = 1 x 10 m, U = 1.5 cm/sec = 0.015 m/sec.
S = 0.9
p = sp=0.9 x 1000 = 900 kg/m³
If weight of bubble is neglected, the drag force and the buoyancy force must keep the bubble in equilibrium.
Drag force = Buoyant force
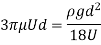
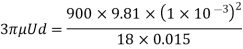

Check Reynolds number

The expression for drag force is valid only for Reynolds’s number less than unity.
Q.2 A viscometer consisting of a long vertical tank containing a fluid at the desired ambient conditions and a small sphere is employed for determining the velocity of an oil. If a steel sphere (S=0.8) of 1 cm diameter falls with a constant velocity of 5 cm/s through a lubricating oil (S = 0.9). calculate the velocity of the oil.
Soln.:
Given: 5, -0.8, d=1 cm = 1x 10¹ m. U-5 cm/s 0.05 m/s, S₁-0.9
Density of sphere
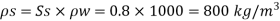
Density of fluid (oil)
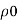 = 0.9 x 1000=900 kg/m
= 0.9 x 1000=900 kg/m
Viscosity for falling sphere is given by
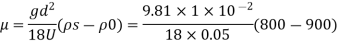
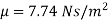
Check Reynolds number
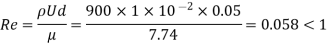
Q.3 In a torsional viscometer, the outer cylinder of 150.5 mm diameter is rotated by turning shaft at a constant speed of 100 rpm. Owing to viscosity, the liquid under test transmits a torque of 540 Nm to the inner cylinder of 150 mm diameter, which is suspended by torsion wire fixed at its upper end. If the liquid is 130 deep, find the viscosity
Soln.:
Given: Inner diameter, D, 150 mm, Outer diameter,
D₁ = 150.5 mm
Number of rotation, N-100 rpm,
Torque, T-540 Nm
h+t= 130
R₁-150/2-75 mm - 0.075 m
R2 = 150./ 2= 75.25 mm=0.07525 m

h = 130-t=130-0.5= 129.5 mm
For torsional viscometer, viscosity is

The viscosity of fluid is 37.36 N.s/m².
Q.4 In a rotating cylinder viscometer, the radii of the cylinders are 32 mm and 30 mm and the outer cylinder is rotated steadily at 200 rpm. For certain liquid filled in the annular space to a depth 80 mm, the torque produced on the inner cylinder is 0.9 x 10 Nm. Calculate viscosity.
Soln.:
Given:
Radius of inner cylinder, R, = 32 mm = 0.032 m.
Radius of outer cylinder, R₂ = 30 mm = 0.03 m,
Height of liquid, h=== 80 mm = 0.08 m,
Speed of cylinder, N = 200 rpm,
Torque T = 0.9 x 10 Nm
For rotating cylinder, viscosity is
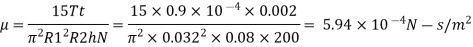
The viscosity of fluid is 5.94 x10* Ns/m².
Q.5 The viscosity of an oil specific gravity 0.8 is measured by a capillary tube of diameter 40 mm. The difference of pressure head between two point 1.2 m apart is 0.3 m of water. The weight of oil collected in a measuring tank is 400 N in 100 seconds. Find the viscosity of oil.
Soln.:
Given: Sp. gr. of oil, S = 0.8,
Wt. Density, p = Sxp = 0.8 x 1000 = 800 kg/m³
Diameter of tube, D = 40 mm = 0.04 m,
Length of tube, L = 1.2 m
Pressure head difference, h = 0.3 m of water,
Time, t= 100 sec., Weight of oil, W = 400 N
Discharge Q = Wt. of oil collected/sec /Weight density
=400/100 /800
= 0.509 x 10³ m³/sec
Viscosity by capillary tube viscometer is given by
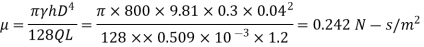
:. The viscosity of oil is 0.242 N-s/m².
Key takeaways
There are 3 types of measurements of viscometer
References: