6.1 Slope and deflection Relation between moments | unit 6 slope and deflection

THERMO

Unit - 6

Slope and Deflection

6.1 Slope and deflection - Relation between moments

The reason of calculating deflection in beam is to decide the vertical intensity of its sag from preliminary horizontal (longitudinal) axis of beam.

The slope is the attitude of beam axis between preliminary function and very last function after deflection.

Deflection of beam controls the powerful duration to intensity ratio of beam.

Consider a simply a supported straight beam subjected to transverse loading. It will deflect about its original axis as shown in fig. the deflected axis of beam is called elastic curve which bends into an arc of a circle with radius of curvature R

The elastic curve is very flat and its slope at any point is very small

Slope tan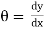

As slope is very small

Neglect tan,

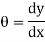
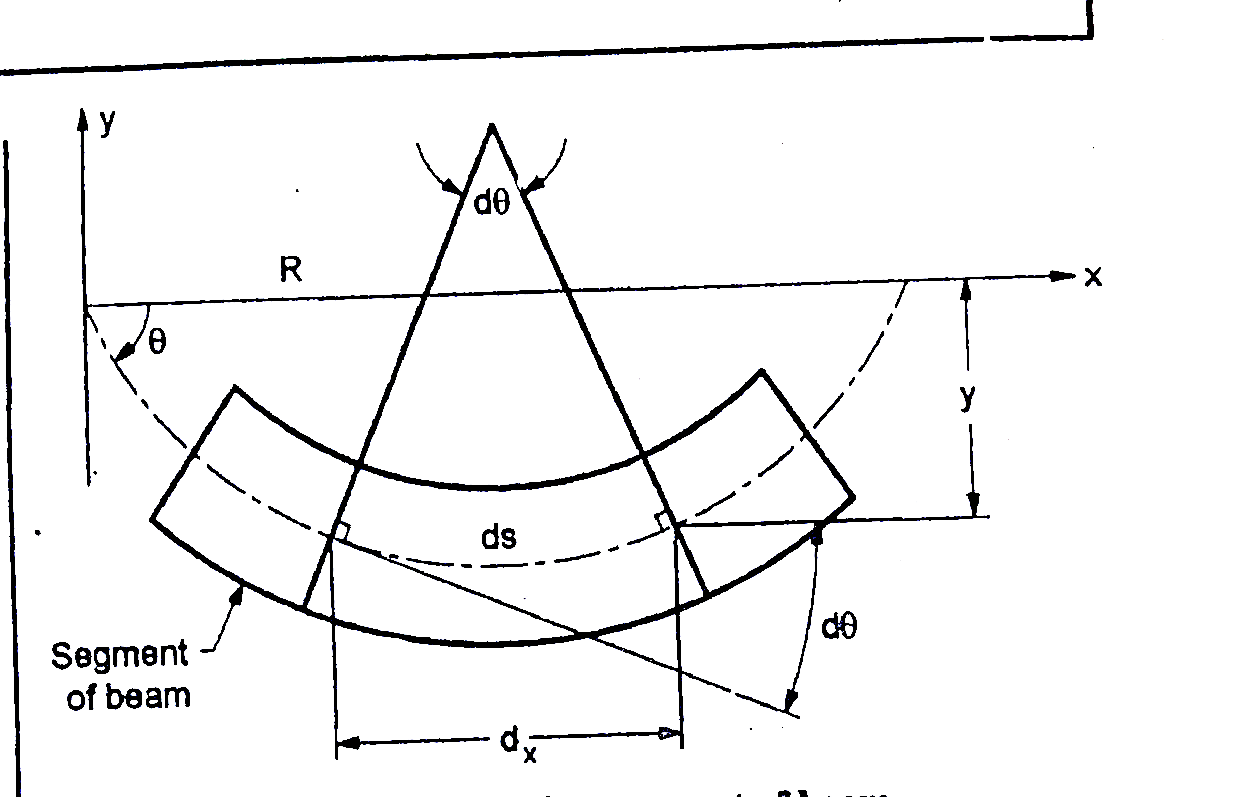
Differentiate w.r.t. x

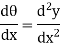
From fig.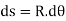

Where R is radius of curvature for arc length ds

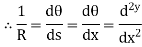
From flexural bending formula

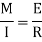
From above equation

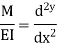
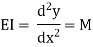
Where EI – is the flexural rigidity of the beam

Is above equation is known as differential equation of the elastic curve of a beam.

However, dx/dy is very small is square is still smaller compared to unity

Integrating equation

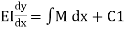
Slope deflection

(As )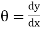

Again integrated w. r. t. x

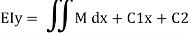
Deflection equation where c1 and c2 are the constant in integration which can be evaluate by using support boundary equation

Key takeaway:

The slope is the attitude of beam axis between preliminary function and very last function after deflection.

Deflection of beam controls the powerful duration to intensity ratio of beam.

Consider a simply a supported straight beam subjected to transverse loading

6.2 Slope and deflection

The approach in the Slope-deflection slope deflection is to consider each beam element separately and to write down the so-called slope deflection equations for each element, in a somewhat mechanical fashion.

These are mental equations relating the unknown end moments (MM) of any prismatic beam AB to the known fixed-end moments (MM) and the slopes (0,0) and sections (A, A,) at the two ends.

For convenience, the deflections can substitute by chord rotations. Some of these displacements may be equal to zero or May Similar equations are written down for elements BC, CD, in a continuous beam

For convenience, the deflections can but substituted by chord rotations. Some of these displacements may be equal to zero or may own similar equations are written down for elements BC, CD... in a continuous beam.

System or a plane frame system. Then, appropriate equilibrium equations are written down, corresponding to the unknown displacements.

For example, in a continuous beam ABCD the equilibrium equation corresponding to the unknown rotation on is given by MA+ Mac Ma, where Ma is the concentrated moment, if any, applied at B.

These equilibrium equations are then solved simultaneously to yield the unknown displacements.

Substituting the values of the displacements in the slope-deflection equations, we get the desired end moments in each beam element, and thereby the other support reactions. We then have the complete force response.

The method appears to be very simple in concept, but can be challenging while dealing with situations involving unknown deflections (or chord rotations), which are sometimes referred to as sway type problems.

In non-sway type problems, there are only unknown end rotations involved, and these are fairly straight-forward to handle. However, even in such problems, there are several short-cuts possible.

For example, if the extreme end A of a continuous beam ABCD has a hinged support or has an overhang beyond it, we recognize that the end moment MA is statically determinate, and we can avoid treating 0, as an unknown. Similarly, we can handle other boundary conditions such as a guided-fixed support and take advantage of symmetry and anti-symmetry.

However, a word of caution is appropriate here. The slope-deflection method should not be applied blindly, when we seek to take short-cuts.

We need to understand the basic concept underlying the displacement method while applying the modified slope-deflection equations and modified fixed-end moments, wherever appropriate. This makes the analysis exercise interesting and challenging.

1. Analysis of fixes beam by S.D method

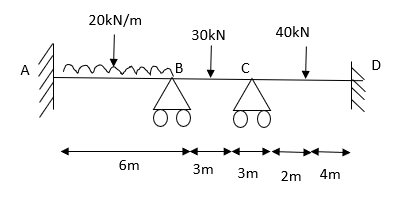
Step 1) Dki = 2

Step 2) Find Fixed End Moments

Solution:

For AB

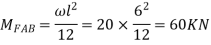
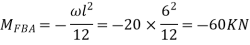
For BC

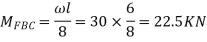
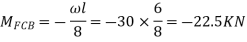
For CD

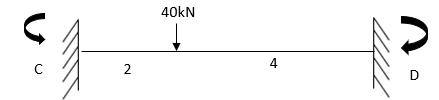
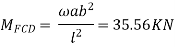
Apply S.D. equation

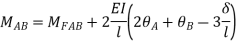
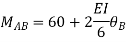
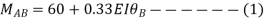
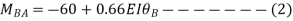
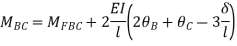
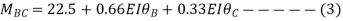
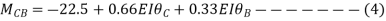
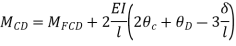
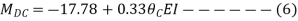
Joint equilibrium condition

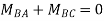
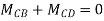
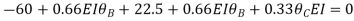
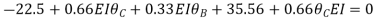
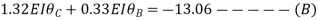
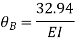
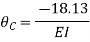
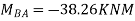
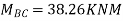
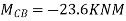
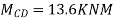
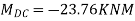
Key takeaway:

In non-sway type problems, there are only unknown end rotations involved, and these are fairly straight-forward to handle.

6.3 Moment area method

Moment area method is used to determine the slope and deflection at a point in determinate structure and indeterminate structures.

Theorems of moment are suggested by Mohr’s and thus these theorems are called as Mohr’s theorem there are two theorem which are explained

First theorem:

The angle between the tangent drawn at two-point B and Aon the deflected curve of a beam is equal to the area under the bending moment diagram between two-point A and B divided by EI

Proof:

Consider a beam is shown in fig. subjected to arbitrary load. The deflected shape and BMD of a beam as shown in fig. respectively

Consider two points C and D at a elements dx on the beam.

The relation between the radius of curvature and BM for any such section is given by

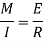
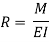
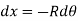
Where negative sign is used with 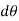since 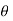decreases with increases in x from a positive maximum value at x=0 to a negative minimum value at x= L

For whole elastic curve

Diagram:

Integrated equation

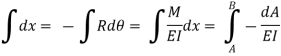
Where, dA= Area of BMD between point C and D

Change of slope between point B and A

= Area of BMD between B and A / EI

This proves first theorem.

Second Theorem:

Statement:

If A and B are two points on the deflected shape of a beam the vertical distance of point B from the tangent drawn to the elastic curve at point A is equal to moment of area of BMD between point A and B about vertical line from point B divided by EI

Proof:

Consider the distance dy along the vertical line through point B as shown in fig is nearly equal to dt = -XB. d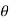

Integrating equation, we get the vertical distance yBA between the point B and the tangent from point A on the deflected beam

yBA = moment of BMD between A and B at B/ EI

Proved

Key takeaway:

Moment area method is used to determine the slope and deflection at a point in determinate structure and indeterminate structures.

Theorems of moment are suggested by Mohr’s and thus these theorems are called as Mohr’s theorem there are two theorem which are explained

The angle between the tangent drawn at two-point B and Aon the deflected curve of a beam is equal to the area under the bending moment diagram between two-point A and B divided by EI

6.4 Macaulay’s method

It is a simple method based on the double integration concept in this method bending moment at any section is expressed in the systematically order.

The section x-x is to be taken in the last portion of the beam

In this method bending moment due to each force or udl is separated by a compartment line.

Slope is obtained by integrating bending moment equation and then deflection is obtained by integration of slope equation.

1. Rules of Macaulay’s method

The section x-x is to be taken in the last portion of the beam

The quantity in the bracket () should be integrated as a whole

The expression for BM(Mxx) equation can be used at any point provided the term within the bracket becomes negative is omitted

Constant of integration C1 and C2 must be written before first vertical line.

2. Step by step procedure:

Determine the support reaction using available condition of equilibrium.

Consider the section x-x at a distance x covering all the loads from left end of the beam

Integrating equation slope equation, we get slope equation

Again, integrate equation we get, deflection equation.

The constant of integration C1 and C2 is calculated by applying boundary condition.

Substitution the value of constant in slope and deflection and write final slope and deflection equation.

Find slope and deflection at any desired point.

Key takeaway:

Determine the support reaction using available condition of equilibrium.

Consider the section x-x at a distance x covering all the loads from left end of the beam

Integrating equation slope equation, we get slope equation

Again, integrate equation we get, deflection equation.

The constant of integration C1 and C2 is calculated by applying boundary condition.

Substitution the value of constant in slope and deflection and write final slope and deflection equation.

Find slope and deflection at any desired point.

6.5 Use of this method to calculate slope and deflection for determinant beam

1. Determinate Beam: the determinate beam is that the beam in which unknown support reactions can be calculated by using static equilibrium equations only.

Example: simply supported beams, cantilever beams, single and double overhanging beams.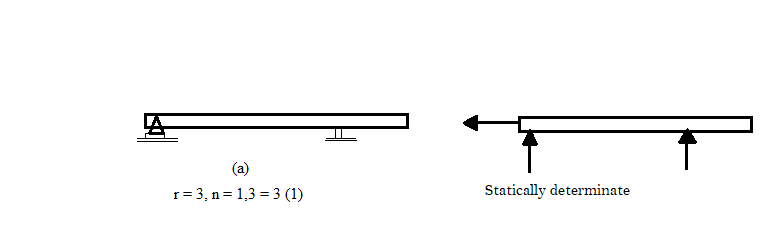

2. Slope and Deflection of beams

Macaulay’s method

(Double ∫∫ method)

(Integration)

3. Basics:

1. Elastic curve: Deformed shape of beam is called as elastic curve.

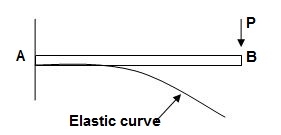
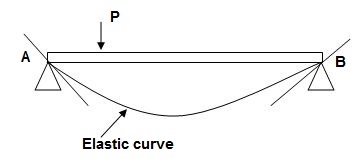
$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\53.JPG$ $C:\Users\TARUNA\Desktop\internship\february\11 feb2020\54.JPG$

2. Slope: Angle made by tangent joint to the elastic curve with x-axis is called as slope.

3. Deflection: Translation of cross-section normal to the longitudinal axes of member is called as deflection.

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\55.JPG$

4. Reference System:

Left end of beam is taken as origin and reference system is as below.

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\56.JPG$

5. Sign conventions:

(A). Slope

ϴ + dy/dx = Anticlockwise rotation of tangent

dy/dx = clockwise rotation of tangent

(B) Deflection

+y = upward Deflection

-y = downward Deflection

6. Flexural Rigidity = (EI)

Product of young modulus of elasticity and moment of inertia of cross-section is called as Flexural rigidity (FI).

Unit: KN.m2

Note: Slope and deflections are inversely proportional to FI.

7. Boundary conditions:

These are nothing but support conditions.

i) At fixed end:

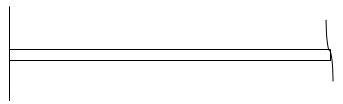
dy/dx = 0

y = 0

ii) At hinged and roller end

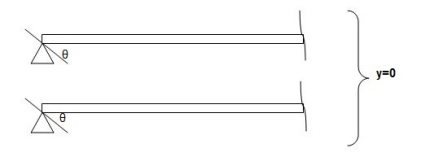
$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\58.JPG$

Q. Write boundary conditions for following beams

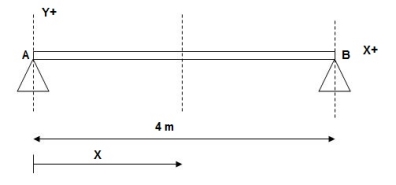
1) $C:\Users\TARUNA\Desktop\internship\february\11 feb2020\59.JPG$

At x = 0; yA = 0

x = 4m; yB = 0

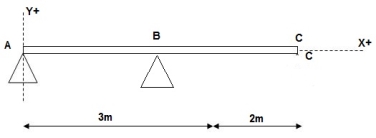
2) $C:\Users\TARUNA\Desktop\internship\february\11 feb2020\60.JPG$

At x = 0; yA = 0

x = 3m; yB = 0

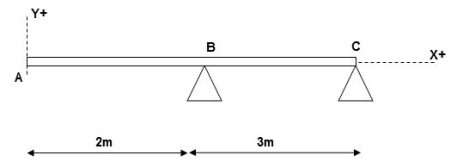
3) $C:\Users\TARUNA\Desktop\internship\february\11 feb2020\61.JPG$

At x = 2m; yB = 0

At x = 5m; yC = 0

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\62.JPG$

At x = 0; {dy/dx} A = 0

X = 0; yA = 0

8. Concept of Macaulay’s Method

We have,

M/I = 6/y = E/R

Where; R = Radius of curvature

= {1 + (dy/dx)2 }3/2 / d2y/dx2

For beams values of dy/dx are very small

R ≈ 1/d2y/dx2

M/I = E/R, E/1/d2y/dx2 = Ed2y/1 x dx2

M/I = Ex (d2y/dx2)

M = EI.d2y/dx2 = - - - - F(x) = BM eqn

ϴ = EI (dy/dx) = ----------- +c1 = slope eqn

Deflection EI(y) = --------- + C1(x) + C2 = Defneqn

(Eqn of elastic curve)

9. B.M equations:

Note:

For writing BM equation always consider section at a distance x from origin, placed in right extreme zone.

Case 1

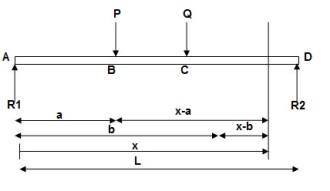
$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\63.JPG$

EI (d2y/dx2) = BMx = R1(x) | - P(x-a) | - Q(x-b)

Case 2

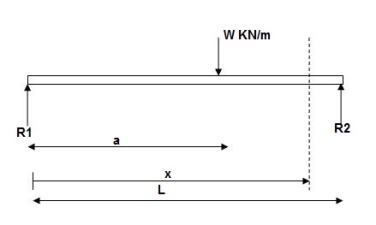
$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\64.JPG$

EI (d2y/dx2) = BMx = R1x | - w(x-a)2/2

EI (d2y/dx2) = BMx = R1(x) | - wx2/2 | + w(x-a)2/2

Case 3:

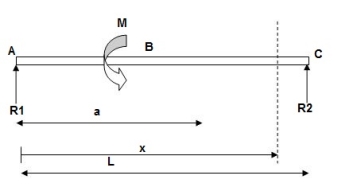
$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\65.JPG$

EI(d2y/dx2) = BMx = R1(x) | - M(x-a)

10. Procedure for Macaulay’s method:

i). Find support reactions

ii). Equations

iii). Find constants C1& C2 using boundary conditions

iv). Find slope &deflection

Notes:

1] Value of FI shall be substituted at the end of calculation in KN m2.

2] Answer for slope will be in radians and deflection in meter (m).

3] For simply supported beam at a section where deflection is maximum, slope is zero.

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\66.JPG$

Example:

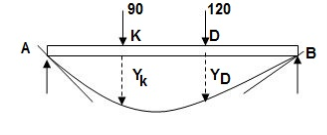
1) Given:

E = 200 GPa = 200 x 103MPa / N/mm2 = 200 KN/mm2

I = 3 x 108 mm4

EI = 200 x 3 x 108 KNmm2

EI = 600 x 102 KNm2

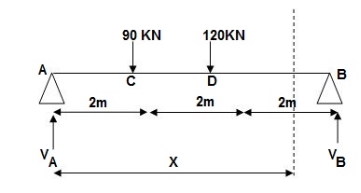
$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\67.JPG$

Reactions,

∑MA = VB (6) – 90 x 2 – 120(4) = 0

VB = 660/6

VB = 110 KN

∑Fy = VA + VB – 90 – 120 = 0

VA = -110 +90+120

VA = 100 KN

∑Fx = HA = 0

EI (d2y/dx2) = 100(x) | - 90(x-2) | -120(x-4) ---(1)

EI (dy/dx) = C1 + 100x2/2 | - 90(x-2)2/2 | -120(x-4)2/2 ---(2)

EI(y) = C1(x) + C2 + 100x3/6 | - 90(x-2)3/6 | -120(x-4)3/6 ---(3)

Boundary conditions:

At x=0 | yA = 0, put in (3)

C2 = 0

At x = 6m, yB = 0, put in (3)

6C1 + 100 x 36 – 90 x (4)3/6 – 120 x 23/6 = 0

6C1 + 3600 – 960 – 160 = 0

6C1 = -2480

C1 = (-) 413.33

Slope &Deflection:

X = 0, in (2),

(dy/dx) A = (-) 413.33/EI = (-)4133.33/600 x 102

= 6.88 x 10-3 rad( )

X = 6m in (2),

EI (dy/dx) B = (-)413.33 + 100(6)2/2 – 90(4)2/2 – 120 x (2)2/2

= - 413.33 + 1800 – 720 – 240 = 426.67

(dy/dx) B = 7.11 x 10-3rad( )

X = 2m in (3),

Yc = -413.33 x 2 + 100 x 23/6

= - 826.66 + 133.33

= -693.22/EI = -693.32/600 x 102 = -11.55

Yc = -11.55 mm( )

X = 4m in (3)

yD = -413.33 x 4 + 100 x 43/6 – 90 x 23/6

= -706.6/EI = -706.6/600 x 102

= - 11.77 mm

yD = 11.77 mm( )

For maximum deflection

Let X > 2m

< 4m - zone CD

EI (dy/dx) CD = - 413.33 + 100/2x2 – 90(x-2)2/2 = 0

-413.33 + 50 x2 – 45(x-2)2 = 0

-413.33 + 50x2 – 45(x2-4x+4) = 0

-413.33 + 5x2 + 180x – 180 = 0

5x2 + 180x – 593.33 = 0

X = 3.03 >2m

<4m

Assumption is correct

X = 3.03m in (3)

Ymax = -413.33 x 3.03 + 100(3.03)3/6 – 90 x (3.03-2)3/6

= -1252.38 + 463.63 – 16.39

= - 805.14/EI

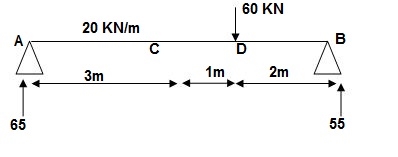
2) Given:

EI = 4 x 104 Kn.m2

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\69.JPG$

Reactions:

∑MA = 0

VB x 6 – 20 x 3 x 1.5 – 60 x 4 = 0

VB = 55KN

∑Fy = 0

VA + VB – 60 – 20 x 3 = 0

VA = 65 KN

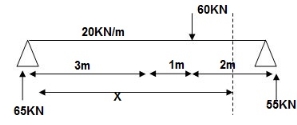
$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\70.JPG$

EI (d2y/dx2) = 65 x x | - 20 x x2/2 | + 20 x (x-3)2/2 | - 60(x - -(1)

EI {dy/dx} = C1 + 65x2/2 | - 20 x x3/6 | + 20(x - 3)3/6 | - 60(x - 4)2/2 - - (2)

EI(y) = C1(x) + C2 + 65x3/6 | - 20 x x4/24 | + 20(x-3)4/24 | -60(x-4)3/6 --(3)

Boundary conditions:

At x=0, yA = 0, put in (3)

C2 = 0

X = 6m, yB = 0 put in 3

C1 x 6 + 65 x 62 – 20 x 63/4 + 20 x 34/24 – 60 x 23/6 = 0

C1 = -207.91

Slope &deflection:

X = 3m in (2)

(dy/dx) c = -207.91 + 65 x 32/2 – 20 x 33/6 = -5.41/EI

= -1.35 x 10-4

(dy/dx) c = 1.35 x 10-4 rad( )

X = 3m in 3

yC = -207.9 x (3) + 65 x (3)3/6 – 20 x 34/24 – 398/EI

= - 9.967 x 10-3

= -9.967mm

yC = 9.967 mm( )

x = 4m in (3)

yD = -207.9 x 4 + 65 x 43/6 – 20 x 43/24 + 20/24

= - 350.7/EI

= 8.76 mm ( )

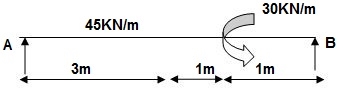
3) Given:

EI = 32.5 x 103 Kn.m2

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\71.JPG$

Reactions:

∑MA = 0

VB (5) – 45 x 3 x 1.5 + 30 = 0

VB = 34.5 KN

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\72.JPG$

EI {d2y/dx2} = 100.5 x x – 45x2/2 | + 45 x (x-3)2/2 | -30(x-4)0 -- (1)

EI {dy/dx} = C1 + 100.5x2/2 – 45x3/6 | + 45 x (x-3)3/6 | - 30(x-4) --(2)

EI(y) = C1(x) + C2 + 100.5x3/6 – 45x4/24 | + 45 x (x-3)4/24 | - 3(x-4)2/2 --(3)

Boundary conditions:

At x=0; yA = 0 put in eqn3

C2 = 0

At x=5; yB = 0

5C1 + 100.5 x 53/6 – 45(5)4/24 + 45(2)4/24 – 30/2 = 0

C1 = (-) 187.375

Slope &Deflection:

X=3m in (2)

(dy/dx) c = -187.375 + 100.5 x 32/2 – 45(3)3/6

= 62.375/32.5 x 103

(dy/dx) c = 1.919 rad( )

X = 3m in (3)

yC = -187.375 x 3 + 100.5 x 33/6 – 45 x 34/24

= - 261.75/32.5 x 103

= - 8.053mm

yC = 8.053mm( )

x = 4m in (3)

yD = -187.375 x 4 + 100.5 x (4)3/6 – 45 x (4)4/24 + 45/24

= - 155.625/32.5 x 103

= - 4.78 mm

yD = 4.78 mm( )

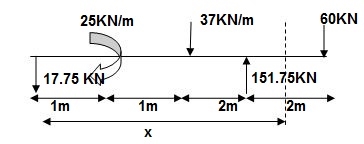
Q. Find deflection of given beam?

Given:

E = 200 GPa

I = 6.2 x 107mm4

EI = 200 x 6.2 x 107 KN.mm2

= 200 x 6.2 x 107 x 10-6 KNm2

EI = 12400 KNm2

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\73.JPG$

Reactions:

∑MA = 0

VB x 4 – 25 – 37(2)(3) – 60(6) = 0

VB = 151.75 KN

VA + VB – 60 – 37 x 2 = 0

VA = (-)217.75 KN

$C:\Users\TARUNA\Desktop\internship\february\11 feb2020\74.JPG$

EI {d2y/dx2} = -17.75 x | + 25(x-1)0 | - 37 x (x-2)2/2 | + 151.75(x-4)2/2 | + 37 x (x-4)2/2 --(1)

EI {dy/dx} = C1 – 17.75x2/2 | + 25(x-1) | - 37(x-2)3/6 | + 151.75(x-4)2/2 | + 37(x-4)3/6 --- (2)

EI(y) = C1x + C2 – 17.75 x3/6 | +25(x-1)2/2 | -37(x-2)4/24 | + 151.75(x-4)3 | + 37(x-4)4/24 ---(3)

Boundary condition:

At x=0; yA=0 C2 = 0 (in eqn (3))

At x=4; yB=0 put in eqn (3)

4C1 – 17.75 x 43/6 + 25 x 32/2 – 37 x 23/6 = 0

C1 = 25.4

Slope and deflection:

X = 2m in (2) & (3)

(dy/dx) D = 25.4 –17.75 x 2 + 25

= 14.9/EI

(dy/dx) D = 1.201 x 10-3rad( )

yD = 25.4 x 2 – 17.75 x 23/2 + 25/2

= 39.63/12400

yD = 3.196 mm( )

x = 6m in (2) & (3),

(dy/dx) E = 25.4 – 17.75 x 62/2 + 25 x 5 – 37(4)3/6 + 151.75(2)2/2 + 37 x 23/6

= -210.183/12400

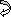= 0.017 rad( )

YE = - 341.7/12400 = 27.5mm

Key takeaway:

Find support reactions

Equations

Find constants C1& C2 using boundary conditions

Find slope &deflection

References:

Timoshenko, S. and Young, D. H., “Elements of Strength of Materials”, DVNC, New York USA.

Kazmi, S. M. A., “Solid Mechanics” TMH, Delhi, India.

Hibbeler, R. C. Mechanics of Materials. 6th ed. East Rutherford, NJ: Pearson Prentice Hall, 2004

Crandall, S. H., N. C. Dahl, and T. J. Lardner. An Introduction to the Mechanics of Solids 2nd ed. New York, NY: McGraw Hill, 1979

Laboratory Manual of Testing Materials - William Kendrick Hall

Mechanics of Materials - Ferdinand P. Beer, E. Russel Jhonston Jr., John T. DEwolf – TMH 2002.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined