Unit - 8
Thin Cylinders and Spheres
Thin cylindrical shell is likewise termed as a strain vessel and such vessels are typically utilized in numerous engineering applications along with for storing the fluid below strain.
Boilers, LPG cylinders, Air receiver tanks are the satisfactory examples of skinny cylindrical shells.
A cylindrical or round shell might be considered as skinny cylindrical or round shell, if the wall thickness of shell is very small compared to the inner diameter of the shell.
Wall thickness of a skinny cylindrical and round shell might be identical or much less than the 1/20 of the inner diameter of shell.
Hoop pressure
Stress appearing alongside the circumference of skinny cylinder might be termed as circumferential pressure or hoop pressure.
If fluid is saved below strain internal the cylindrical shell, strain might be appearing vertically upward and downward over the cylindrical wall.
Pressure vessel will have a tendency to burst as displayed right here in following parent and stresses advanced in such failure of cylindrical shell might be termed as circumferential pressure or Hoop pressure.
Cylindrical shell bursting will take location if pressure because of inner fluid strain could be extra than the resisting pressure because of circumferential pressure or hoop pressure evolved within side the wall of the cylindrical shell.
In order to stable the expression for circumferential pressure or hoop pressure evolved within side the wall of the cylindrical shell, we are able to must do not forget the restricting case i.e., pressure because of inner fluid strain have to be identical to the resisting pressure because of circumferential pressure or hoop pressure.
Force due to internal fluid pressure = Internal fluid pressure x Area on which fluid pressure will be acting
Force due to internal fluid pressure = P x (d x L)
Resisting force due to circumferential stress = σH x 2 L t
Force due to internal fluid pressure = Resisting force due to circumferential stress
P x d x L = σH x 2 L t
σH = P x d / (2 t)
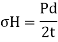
Hoop stress developed in the wall of cylindrical shell.
P = Internal fluid pressure
d = Internal diameter of thin cylindrical shell
t= thickness of the wall of cylinder
L = Length of the cylindrical shell
σH = hoop stress developed in the wall of the cylindrical shell
Key takeaway:
Longitudinal Stress thin-walled pressure vessel: When the vessel has closed ends the inner stress acts on them to expand a pressure alongside the axis of the cylinder. This is called the axial or longitudinal stress and is typically much less than the hoop stress.
d = Mean Diameter
t= outer diameter
The longitudinal stress σ within side the wall of a cylindrical strain vessel containing stress at strain p is given by.
σ = pr 2 t
Spherical shells are extensively used in lots of structural engineering applications inclusive of aerospace vehicles, roof domes, garage tanks, adaptive clever membranes and lively shells, laminated transducers and sensors, ballistic missile bulkhead and submarines
The round shell considered within side the gift study subjected to uniform temperature. The stress applied at the internal floor of the shell. The outer floor of the shell is loose from mechanical load. Thus, the boundary situations of the problem are given by
Trr = – p at r = a
Trr = 0 at r = b
Where,
Trr denote displacement and stress along the radial direction.
When a skinny cylindrical shell is subjected to an inner pressure, its wall be subjected to lateral strain, the impact of which there may be alternate in dimensions (i.e., duration and diameter) of the shell.
Stress performing alongside the duration of skinny cylinder will be termed as longitudinal stress.
If fluid is saved be neat stress internal the cylindrical shell, stress pressure could be performing alongside the duration of the cylindrical shell at its ends. Cylindrical shell will generally tend to burst as displayed right here in following parent and stresses evolved in such failure of cylindrical shell could be termed as longitudinal stress.
Longitudinal stress = (1/2) x Circumferential stress
σL = 1/2 x [p x d]/2t
σL = p.d/4t
Key takeaway:
References: