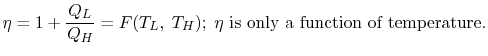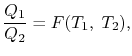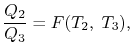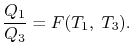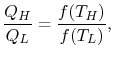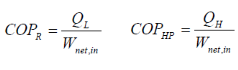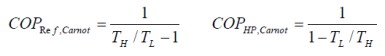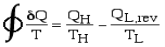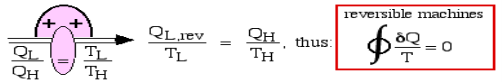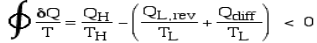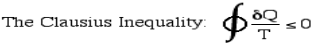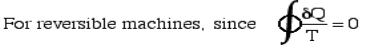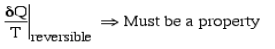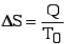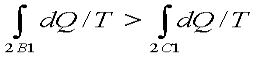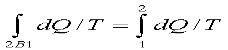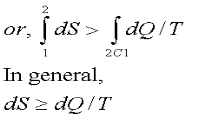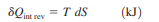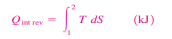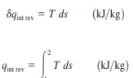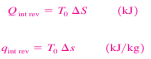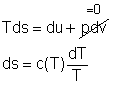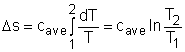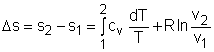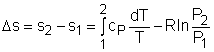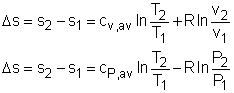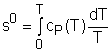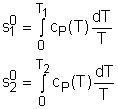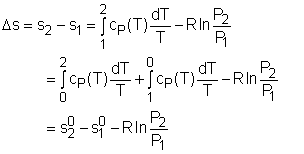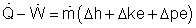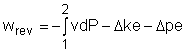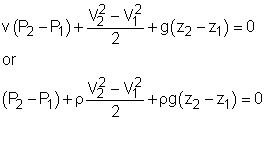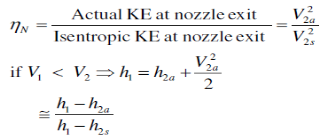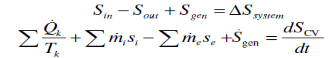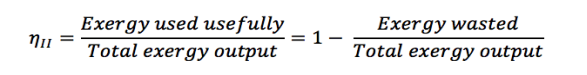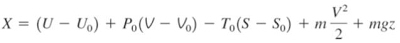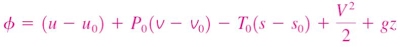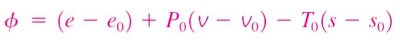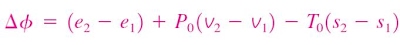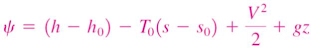Unit - 3
Second Law of Thermodynamics
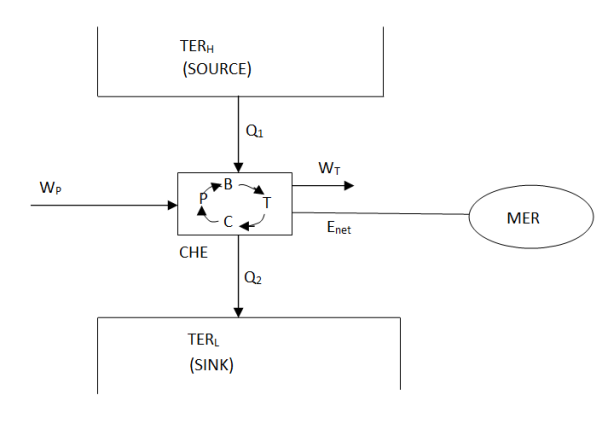
A thermal energy reservoir (TER) is defined as a large body of infinite heat capacity, which is capable of absorbing or rejecting an unlimited quantity of heat without suffering appreciable changes in its thermodynamic coordinates. The changes that do take place in the large body as heat enters or leaves are so very slow and so very minute that all processes within it are quasi-static.
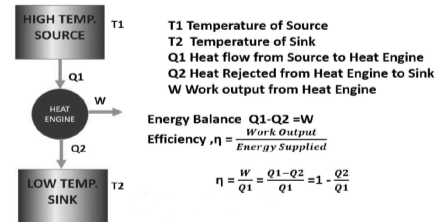
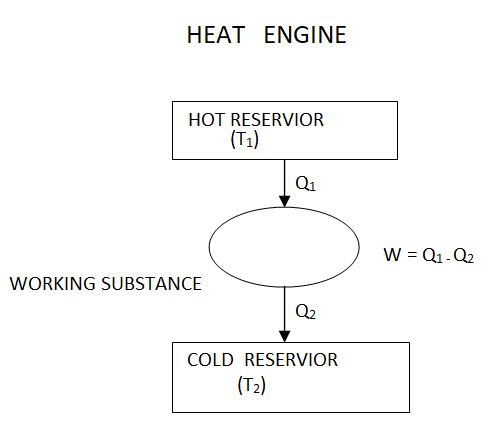
The thermal energy reservoir TER from which heat Q1 is transferred to the system operating in a heat engine cycle is called the source. The thermal energy reservoir TER to which heat Q2 is rejected from the system during a cycle is the sink.
A typical source is a constant temperature furnace where fuel is continuously burnt, and a typical sink is a river or sea or the atmosphere itself.
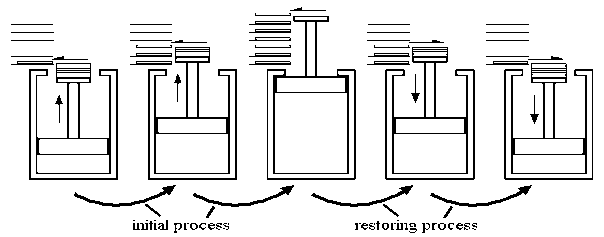
A mechanical energy reservoir (MER) is a large body enclosed by an adiabatic impermeable wall capable of storing work as potential energy (such as a raised weight or wound spring) or kinetic energy (such as a rotating flywheel). All processes of interest within an MER are essentially quasi- static. An MER receives and delivers mechanical energy quasi - statically.
|
Fig 1
Above figure show a cyclic heat engine exchanging heat with a source and a sink and delivering W(net) in a cycle to an MER
Whether it is coal, oil, gas or nuclear power, 80% of the world’s electricity is derived from heat sources and almost all of the energy conversion processes used convert the thermal energy into electrical energy involve an intermediate step of converting the heat energy to mechanical energy in some form of heat engine. To satisfy this need a wide range of energy conversion systems has been developed to optimise the conversion process to the available heat source.
|
Fig 2
Despite over 250 years of development since James Watt's steam engine was first fired up, the best conversion efficiency achieved today is only around 60% for combined cycle steam and gas turbine systems. Efficiencies in the range of 35% to 45% are more common for steam turbines, 20% to 30% for piston engines and as low as 3% for OTEC ocean thermal power plants.
The efficiency of heat engines was first investigated by Carnot in the 1824 and expanded upon by Chaperon who provided analytical tools in 1834 and Kelvin who stated the Second Law of Thermodynamics in 1851 and finally by Clausius who introduced the concept of entropy in 1865.
Every thermodynamic system exists in a particular state which is defined by the properties of its components such as heat, temperature, pressure, volume, density, entropy and phase (liquid, gas etc) at a given point in time. Thermodynamics concerns the conversions between heat and other forms of energy in the system and the related energy flows.
In a thermodynamic cycle, energy is applied in one form to change the state of the system and energy is then extracted in a different form to return the system to its original state. In a heat engine, the energy is applied in the form of heat to change the state of a working fluid and then extracted in the form of mechanical work to return the working fluid to its initial state. In other words, a heat engine is a system in which energy is interchanged between an energy conversion system and its surroundings.
It is important to note that though the working fluid in a heat engine may work in a closed cycle, the "system" and the "state of the system" are defined to include the physical "engine" as well as the working environment or surroundings.
Key takeaways
- Every thermodynamic system exists in a particular state which is defined by the properties of its components such as heat, temperature, pressure, volume, density, entropy and phase (liquid, gas etc.) at a given point in time.
- Thermodynamics concerns the conversions between heat and other forms of energy in the system and the related energy flows.
Kelvin-Planck statement
It is impossible to convert all the heat extracted from a hot body into work. In the heat engine, the working substance takes heat from the hot body, converts a part of it into work and gives the rest to the cold body. There is no engine that can convert all the heat taken from the source into work, without giving any heat into the sink. This means that for obtaining continuous work, a sink is necessary.
Clausius statement
It is not at all possible to transfer heat from a cold body to a hot body without the expenditure ofwork by an external energy source or its states that the heat energy cannot transfer from a body at a lower temperature to a body at a higher temperature without the addition of energy.
For example- There is a refrigerator that transfers an amount of heat from a cold body to a hot body without having any supply of external energy. So this is the violation ofClausius statement. Now suppose an engine working between the same hot and cold bodies takes in heat from hot body converts a part W into work and gives the remaining heat to the cold body.
The engine alone does not violate the second law of thermodynamics. But if the engine and refrigerator combine together, they form a device that takes up all the heat from the hot body and converts all into work without giving up any amount to the cold body. It violets the Kelvin-Planck statement. So we say that the two statements of the second law of thermodynamics are equal in all respects
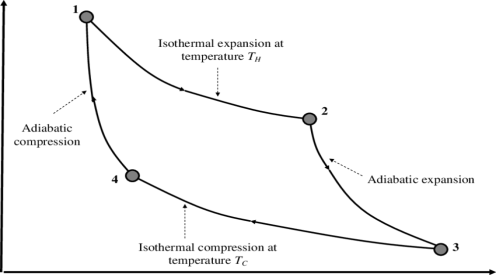
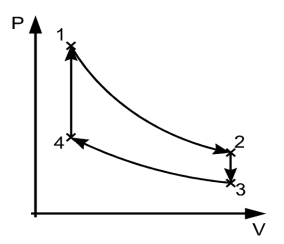
Carnot cycle, in heat engines, ideal cyclical sequence of changes of pressures and temperatures of a fluid, such as a gas used in an engine. It is used as a standard of performance of all heat engines operating between a high and a low temperature.
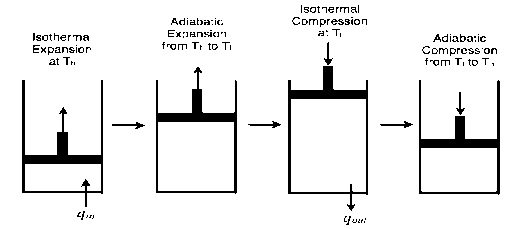
In the cycle the working substance of the engine undergoes four successive changes: expansion by heating at a constant high temperature; reversible adiabatic expansion; compression by cooling at a constant low temperature; and reversible adiabatic compression. The engine receives heat (from the heat source) during the expansion at high temperature, delivers work during the reversible adiabatic expansion, rejects heat (to the heat sink) during the compression at low temperature, and receives work during the reversible adiabatic compression. The ratio of the network output to the heat input is equal to the ratio of the difference between the temperatures of the heat source and the heat sink divided by the temperature of the heat source. It represents Carnot’s principle in that it is the largest such ratio of any engine operating between the two temperatures.
The Carnot cycle consists of the following four processes:
- A reversible isothermal gas expansion process. In this process, the ideal gas in the system absorbs qin amount heat from a heat source at a high temperature Thigh, expands and does work on surroundings.
- A reversible adiabatic gas expansion process. In this process, the system is thermally insulated. The gas continues to expand and do work on surroundings, which causes the system to cool to a lower temperature, Tlow.
- A reversible isothermal gas compression process. In this process, surroundings do work to the gas at Tlow, and causes a loss of heat, qout.
- A reversible adiabatic gas compression process. In this process, the system is thermally insulated. Surroundings continue to do work to the gas, which causes the temperature to rise back to Thigh.
|
Figure 3: An ideal gas-piston model of the Carnot cycle.
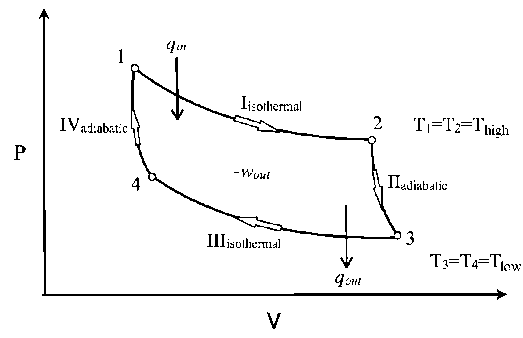
The P-V diagram of the Carnot cycle is shown in Figure. In isothermal processes I and III, ∆U=0 because ∆T=0. In adiabatic processes II and IV, q=0.
|
Fig 4
Carnot’s Theorem
It is impossible for any heat engine to be more efficient than a Carnot engine when operating between two given temperatures:
ηmax = ηcarnot
Consider a heat engine drawing heat Q1 from a heat reservoir at temperature T1, delivering work W and dumping heat Q2 into a heat sink at temperature T2.
The heat engine operates in cycles, that is, it takes in heat Q1, does work W, dumps heat Q2, and in the end returns back to its original unchanged state.
|
Consider the net change in entropy ΔS of the universe: The heat reservoir releases a heat Q1 at a constant temperature T1. Thus the change in its entropy is ∆S1 = -Q1/T1 The heat sink accepts heat Q2 at a constant temperature T2. Thus the change in its entropy is ∆S2 = Q2/T2 Thus the net change in entropy of the universe is ∆S=∆S1+ ∆S2 = Q2/T2 – Q1/T1 Using the second law of thermodynamics, ΔS≥0, which implies Q2/T2-Q1/T1≥ 0 Q2/T2 ≥ Q1/T1 Q2/Q1 ≥ T2/T1 1-Q2/Q1≤ 1-T2/T1 Since the left-hand side represents the efficiency of the given heat engine (η) and the right-hand side is the efficiency of a Carnot engine, η ≤ ηcarnot=ηmax=ηcarnot
|
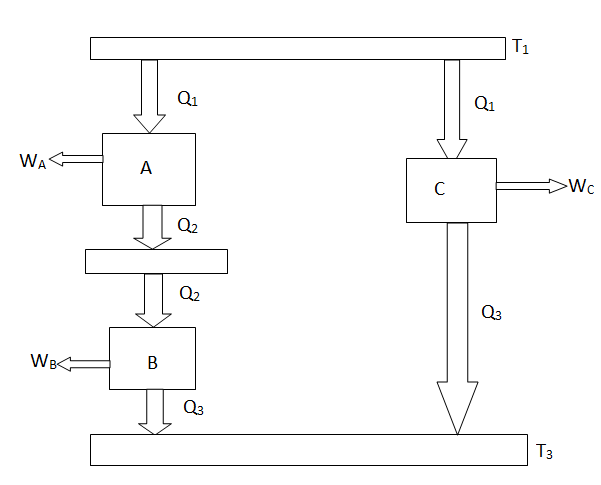
The considerations of Carnot cycles in this section have not mentioned the working medium. They are thus not limited to an ideal gas and hold for Carnot cycles with any medium. Earlier we derived the Carnot efficiency with an ideal gas as a medium and the temperature definition used in the ideal gas equation was not essential to the thermodynamic arguments. More specifically, we can define a thermodynamic temperature scale that is independent of the working medium. To see this, consider the situation shown below in Figure 6.2, which has three reversible cycles. There is a high temperature heat reservoir at T1and a low temperature heat reservoir at T3For any two temperatures T1,T2the ratio of the magnitudes of the heat absorbed and rejected in a Carnot cycle has the same value for all systems.
Figure 5: Arrangement of heat engines to demonstrate the thermodynamictemperature scale
Also
But
Hence
We thus conclude that F (T1,T2) has the form f(T1)/f(T2) and Similarly F (T2,T3)= f(T2)/f(T3). The ratio of the heat exchanged is therefore
In general,
So that the ratio of the heat exchanged is a function of the temperature. We could choose any function that is monotonic, and one choice is the simplest: f (T) =T This is the thermodynamic scale of temperature, QH/QL = TH/TLThe temperature defined in this manner is the same as that for the ideal gas; the thermodynamic temperature scale and the ideal gas scale are equivalent.
|
A Carnot engine or Carnot heat engine is an idealised engine whose working is perfectly reversible. This engine uses an ideal gas as the working substance and performs a 4-stroke process to complete one cycle.
It takes heat Q1 from source and rejects heat Q2 to sink and performing an amount of work W=Q1−Q2
|
Fig 6
The Carnot's engine is a reversible engine working between two temperature limits.
The complete cycle functions are given below
|
Fig 7 P-V Diagram
1) Reversible Isothermal expansion heat addition at the constant temperature T1 or TH
2) Reversible Adiabatic expansion of ideal gas. In this process, the temperature of the ideal gas falls from source temperature T1 to sink temperature T2.
3) Reversible Isothermal compression of ideal gas at sink temperature T2 or TC. In doing so, it rejects heat Q2 to the sink.
4) Reversible Adiabatic compression of ideal gas where the temperature naturally raises from T2 to T1 and thus the working substance returns to its original state completing the cycle.
The efficiency is given as η= Work done / Heat input Thus, W=Q1−Q2 and heat input is obviously Q1 This gives, η= W/Q1 =1−Q2/Q1 It may be shown thermodynamically that Q2/Q1 = T2/T1. |
Key takeaways
2. The efficiency is given as η= Work done / Heat input Thus, W=Q1−Q2 and heat input is obviously Q1 This gives, η= W/Q1 =1−Q2/Q1
|
A refrigerator or a heat pump that operates on the reversed Carnot cycle is called a Carnot refrigerator or a Carnot heat pump. The coefficient of performance(COP) of reversible or irreversible refrigerator or heat pump is given by COPR = 1/((QH/QL)-1) COPHP = 1/(1-(QL/QH)) Where QH = the amount of heat rejected to the For reversible refrigerators or heat pumps, such as Carnot refrigerators, or Carnot heat pumps, the COPs can be determined by replacing the heat transfer ratios in the above equations by the absolute temperature ratios. These are, COPR,rev = 1/ ((TH/TL)-1) COPHP,rev = 1/ (1-(TL/TH)) where
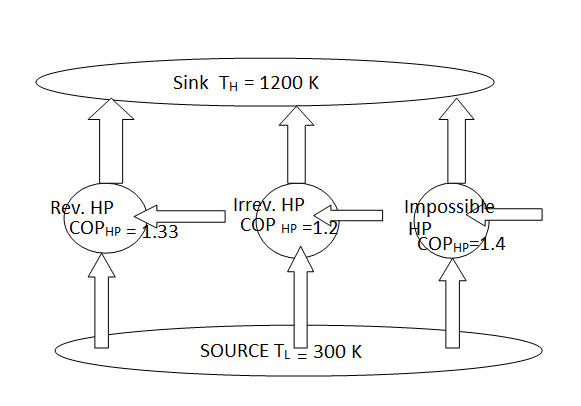
Fig 8The Carnot Heat Pump Has the Highest COP COPR,rev (or COPHP,rev) is the highest COP a refrigerator (or a heat pump) which operates between a high-temperature reservoir at temperature TH and a low-temperature reservoir at temperature TL can reach. All irreversible refrigerators or heat pumps working between the same two reservoirs have lower COPs.
Coefficient of Performance (COP) The performance of refrigerators and heat pumps is expressed in terms of coefficient of performance (COP):
The reversed Carnot cycle is the most efficient refrigeration cycle operating between two specified temperature levels. It sets the highest theoretical COP. The coefficient of performance for Carnot refrigerators and heat pumps are:
|
Key takeaways
- COPR = 1/((QH/QL)-1)
- COPHP = 1/(1-(QL/QH))
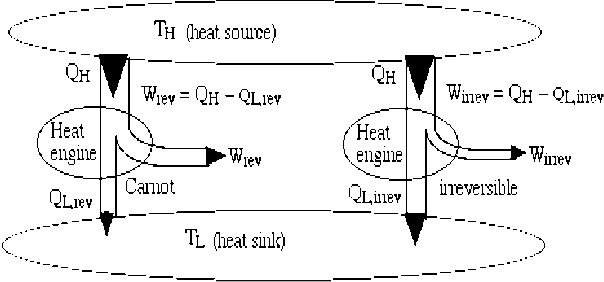
Consider two heat engines, one a reversible (Carnot) engine and the other an irreversible heat engine. For purposes of developing the Clausius Inequality we assume that both engines are sized to accept the same amount of heat QH from the thermal source. Thus since the irreversible engine must be less efficient than the Carnot engine, it must reject more heat QL,irrev to the thermal sink than that rejected by the Carnot engine QL,rev , as shown:
Fig 9 Consider first the reversible (Carnot) heat Engine. Reversible heat transfer can only occur isothermally, thus the cyclic integral of the heat transfer divided by the temperature can be evaluated as follows:
whenever we considered the efficiency of a reversible heat engine, we went into "meditation mode", replacing the ratio of heat flows with the ratio of temperatures:
Notice from the above diagram showing the two heat engines that for an irreversible engine having the same value of heat transfer from the thermal source QH as the reversible engine, the heat transfer to the thermal sink QL,irrev>QL,rev.
Thus finally, for any reversible or irreversible heat engine we obtain the Clausius Inequality:
Defining the property Entropy - S All properties (such as pressure P, volume V, etc) have a cyclic integral equal to zero.
Define = In the case of an isothermal process at temperature T0 we obtain:
|
Concept of entropy
Entropy is defined as a measure of randomness or disorder of a system.
Apart from the general definition, there are several definitions that one can find for this concept.
From a thermodynamics viewpoint of entropy, we do not consider the microscopic details of a system. Instead, entropy is used to describe the behaviour of a system in terms of thermodynamic properties such as temperature, pressure, entropy, and heat capacity. This thermodynamic description took into consideration the state of equilibrium of the systems. Meanwhile, the statistical definition which was developed at a later stage focused on the thermodynamic properties which were defined in terms of the statistics of the molecular motions of a system. Entropy is a measure of the molecular disorder.
By the Clausius definition, if an amount of heat Q flows into a large heat reservoir at temperature T above absolute zero, then the entropy increase is ΔS = Q/T. This equation effectively gives an alternate definition of temperature that agrees with the usual definition. Assume that there are two heat reservoirs R1 and R2 at temperatures T1 and T2 (such as the stove and the block of ice). If an amount of heat Q flows from R1 to R2, then the net entropy change for the two reservoirs is
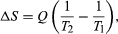
The condition ΔS ≥ 0 determines the maximum possible efficiency of heat engines—that is, systems such as gasoline or steam engines that can do work in a cyclic fashion. Suppose a heat engine absorbs heat Q1 from R1 and exhausts heat Q2 to R2 for each complete cycle. By conservation of energy, the work done per cycle is W = Q1 – Q2, and the net entropy change is ∆S=Q2/T2-Q1/T1
To make W as large as possible, Q2 should be as small as possible relative to Q1. However, Q2 cannot be zero, because this would make ΔS negative and so violate the second law. The smallest possible value of Q2 corresponds to the condition ΔS = 0, yielding (Q2/Q1)MIN=T2/T1as the fundamental equation limiting the efficiency of all heat engines. A process for which ΔS = 0 is reversible because an infinitesimal change would be sufficient to make the heat engine run backward as a refrigerator.
Which is positive provided that T1 > T2. Thus, the observation that heat never flows spontaneously from cold to hot is equivalent to requiring the net entropy change to be positive for a spontaneous flow of heat. If T1 = T2, then the reservoirs are in equilibrium, no heat flows, and ΔS = 0.
Properties of Entropy
- It is a thermodynamic function.
- It is a state function. It depends on the state of the system and not the path that is followed.
- It is represented by S but in the standard state, it is represented by S°.
- It’s SI unit is J/Kmol.
- It’s CGS unit is cal/Kmol.
- Entropy is an extensive property which means that it scales with the size or extent of a system.
- Entropy order: gas>liquid>solids
Entropy Change and Calculations
During entropy change, a process is defined as the amount of heat emitted or absorbed isothermally and reversibly divided by the absolute temperature. Entropy formula is given as; ∆S = qrev,iso/T If we add the same quantity of heat at a higher temperature and lower temperature, randomness will be maximum at a lower temperature. Hence, it suggests that temperature is inversely proportional to the entropy. Total entropy change, ∆Stotal =∆Ssurroundings+∆Ssystem Total entropy change is equal to the sum of entropy change of system and surroundings.If the system loses an amount of heat q at a temperature T1, which is received by surroundings at a temperature T2 So,∆Stotal can be calculated ∆Ssystem=-q/T1 ∆Ssurrounding=q/T2 ∆Stotal=-q/T1+q/T2 ●If∆Stotal is positive, the process is spontaneous. ●If∆Stotal is negative, the process is non-spontaneous. ●If∆Stotal is zero, the process is at equilibrium. Entropy change during the isothermal reversible expansion of an ideal gas ∆S = qrev,iso/T According to the first law of thermodynamics, ∆U=q+w For the isothermal expansion of an ideal gas, ∆U = 0 qrev = -wrev = nRTln(V2/V1) Therefore, ∆S = nRln(V2/V1) For an adiabatic process heat exchange will be zero(q=0), therefore reversible adiabatic expansion is taking place at a constant entropy (isentropic), q = 0 Therefore, ∆S = 0 Even though the reversible adiabatic expansion is isentropic, irreversible adiabatic expansion is not isentropic. ∆S not equal to Zero.
|
Key takeaways
- The net entropy change for the two reservoirs is
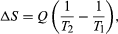
2. Total entropy change,
∆Stotal =∆Ssurroundings+∆Ssystem
3. Temperature. Entropy formula is given as;
∆S = qrev,iso/T
∆S = qrev,iso/T If we add the same quantity of heat at a higher temperature and lower temperature, randomness will be maximum at a lower temperature. Hence, it suggests that temperature is inversely proportional to the entropy. Total entropy change, ∆Stotal =∆Ssurroundings+∆Ssystem Total entropy change is equal to the sum of entropy change of system and surroundings.If the system loses an amount of heat q at a temperature T1, which is received by surroundings at a temperature T2 So,∆Stotal can be calculated ∆Ssystem=-q/T1 ∆Ssurrounding=q/T2 ∆Stotal=-q/T1+q/T2 ●If∆Stotal is positive, the process is spontaneous. ●If∆Stotal is negative, the process is non-spontaneous. ●If∆Stotal is zero, the process is at equilibrium. Entropy change during the isothermal reversible expansion of an ideal gas ∆S = qrev,iso/T According to the first law of thermodynamics, ∆U=q+w For the isothermal expansion of an ideal gas, ∆U = 0 qrev = -wrev = nRTln(V2/V1) Therefore, ∆S = nRln(V2/V1) Entropy Change during Reversible Adiabatic Expansion For an adiabatic process heat exchange will be zero(q=0), therefore reversible adiabatic expansion is taking place at a constant entropy (isentropic), q = 0 Therefore, ∆S = 0 Even though the reversible adiabatic expansion is isentropic, irreversible adiabatic expansion is not isentropic. ∆S not equal to Zero. |
The entropy of the isolated system is the measure of the irreversibility undergone by the system. More is the irreversibility more increase is the entropy of the system. As such the reversible process is an ideal process and it never really occurs. This means the certain amount of the irreversibility is always there in the system, this also means that the entropy of the isolated system always goes on increasing, it never reduces. Here let us keep in mind that isolated system can always be formed by including any system and surroundings within a single boundary.
“An irreversible process always tends to take the isolated system to a state of greater disorder. An isolated system always tends to a state of greater entropy. It may be roughly said that the entropy of a system is a measure of degree of molecular disorder existing in the system. When the heat is imparted to a system, the disorderly motion of the molecules increases and so the entropy of the system increases. The reverse occurs when the heat is removed from the system.”
The first and second law of thermodynamics can be Summarizing in Clausiustwo statements:
Thus the entropy of the isolated system tends to go on increasing and reaches maximum value at the state of equilibrium. When the system reaches equilibrium the increase in entropy becomes zero. Let a system change from state 1 to state 2 by a reversible process A and return to state 1 by another reversible process B. Then 1A2B1 is a reversible cycle. Therefore, the Clausius inequality gives:
If the system is restored to the initial state from 1 to state 2 by an irreversible process C, then 1A2C1 is an irreversible cycle. Then the Clausius inequality gives:
Subtracting the above equation from the first one,
Since the process 2B1 is reversible,
Where the equality sign holds good for a reversible process and the inequality sign holds good for an irreversible process. Now let us apply the above result to evaluate the entropy change of the universe when a system interacts with its surroundings and exchanges energy as heat with the surroundings.
Let Tsur and Tsys be the temperatures of the surroundings and the system such that Tsur >Tsys Let dQ represent the energy transfer as heat from the surroundings to the system during the given irreversible process.
dSsys = dQ/Tsys dSsur = -dQ/Tsur dSuni = dSsys + dSsur = (dQ/T)sys - (dQ/T)sur >0
DSuni >0 (since Tsur>Tsys)
If the system is isolated, there is no change in the entropy of the surroundings and DS = 0, for an isolated system. Therefore the entropy of an isolated system either increases or, in the limit, remains constant. The equality sign holds good when the process undergone by the system is reversible, the inequality sign holds good if there is any irreversibility present in the process. This statement is usually called the principle of entropy increase.Irreversible or spontaneous processes can occur only in that direction for which the entropy of the universe or that of an isolated system, increases. These processes cannot occur in the direction of decreasing entropy.
For an isolated system,
DS > 0, for irreversible processes DS = 0, for reversible processes DS < 0, the process is impossible |
Perpetual motion Defined as “motion that continues forever without any external influences or additions”.The first machines were based on mechanical wheels, hanging weights, and flowing water.
There are three main classifications of perpetual motion machines, those of the first, second, or third kind.
Machines of the First Kind:
Machines of the first kind produce work without any energy being input to the machine. This is a clear violation of the first law of thermodynamics, which says energy can neither be created, nor destroyed – only converted.
Machines of the Second Kind:
The second kind converts thermal energy into work, without any other inputs, at complete efficiency. While this doesn’t violate the first law (no energy is being created, just converted), these machines fall victim to the second law of thermodynamics. Slightly more difficult to understand, a simple breakdown says heat cannot only be taken from something to get work, without having a cooler reservoir to dump some part of that heat (thereby having some loss or inefficiency). Or, stated differently, a system always increases in entropy, or disorder.
Machines of the Third Kind:
Machines of the third kind completely eliminate friction, and therefore continue a motion forever due to inertia. While many have tried, friction cannot be completely and utterly eliminated in any system.
Of the three kinds, machines that approach the third kind are the most useful, namely as a motion storage device. They will never produce energy, or do more work than was put into them, but extremely low friction loss can help to make these devices a reality. For example, in an area with sporadic power service, a heavy weight could be spun up to a high speed when power was available. Then, in times of no power service, the weight could be used to drive a generator. Some of the input energy would be lost to friction as the device spun, but the potential exists for a workable “battery” that could very well outperform traditional technologies in certain situations.
The reversible process is the ideal process which never occurs, while the irreversible process is the natural process that is commonly found in nature. When we tear a page from our books, we cannot change this and ‘un-tear’. This is an irreversible process. Whereas when water evaporates, it can also be condensed in the form of rains. This is a reversible process.
A thermodynamic process is reversible if the process can return back in such a both the system and the surroundings return to their original states, with no other change anywhere else in the universe. It means both system and surroundings are returned to their initial states at the end of the reverse process.
|
Fig 10
In the figure above, the system has undergone a change from state 1 to state 2. The reversible process can reverse completely and there is no trace left to show that the system had undergone thermodynamic change. During the reversible process, all the changes in state that occur in the system are in thermodynamic equilibrium with each other.
The process is internally reversible if no irreversibilities occur within the boundaries of the system. In these processes, a system undergoes through a series of equilibrium states, and when the process reverses, the system passes through exactly the same equilibrium states while returning to its initial state.
In externally reversible process no irreversibilities occur outside the system boundaries during the process. Heat transfer between a reservoir and a system is an externally reversible process if the surface of contact between the system and reservoir is at the same temperature.
A process can be reversible only when its satisfying two conditions
- Dissipative force must be absent.
- The process should occur in infinite small time.
|
Fig 11
In simple words, the process which can reverse back completely is a reversible process. This means that the final properties of the system can perfectly reverse back to the original properties. The process can be perfectly reversible only if the changes in the process are infinitesimally small. In practical situations it is not possible to trace these extremely small changes in extremely small time, hence the reversible process is also an ideal process. The changes that occur during the reversible process are in equilibrium with each other.
Irreversible processes are a result of straying away from the curve, therefore decreasing the amount of overall work done. An irreversible process is a thermodynamic process that departs from equilibrium. In terms of pressure and volume, it occurs when the pressure (or the volume) of a system changes dramatically and instantaneously that the volume (or the pressure) do not have the time to reach equilibrium.
|
Fig 12
A classic example of an irreversible process is allowing a certain volume of gas to release into a vacuum. By releasing pressure on a sample and allowing it to occupy a large space, the system and surroundings are not in equilibrium during the expansion process.Here little work occurs. However, there is a requirement of significant work, with a corresponding amount of energy dissipation as heat flows to the environment. This is in order to reverse the process.
Entropy change of pure substances
For most substances, thermodynamic properties are presented in the form of tables because they are too complex to be expressed by simple equations.
In thermo-systems, many working fluids can be used. Water is one of the most common working fluids involved. It is the only liquid presented in this section.
The thermodynamic properties that are commonly used are:
|
Specific entropy (s) (Which will be introduced in the following section), kJ/(kg-K) or Btu/(lb-R)
Saturated Liquid and Saturated Vapor
|
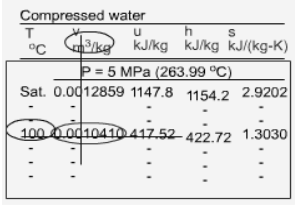
Fig 13 Saturated Water Table
At a given pressure, the temperature at which a pure substance changes phase is called the saturation temperature. At 1 atm, the saturation temperature of water is 100 oC. At a given temperature, the pressure at which a pure substance changes phase is called the saturation pressure. At 100 oC, the saturation pressure of water is 1 atm. The saturation temperature and saturation pressure depends on each other.
There are two types of tables for saturated water. Both tables give the same information. The only difference is that the properties are listed either as a function of temperature or pressure.
The properties listed in the tables include
- Saturation pressure (Psat) for a given temperature or saturation temperature (Tsat) for a given pressure
- Specific volume of saturated liquid (vf) and saturated vapor (vg)
- Specific internal energy of saturated liquid (uf), saturated vapor (ug), and vaporization (ufg = ug - uf)
- Specific enthalpy of saturated liquid (hf), saturated vapor (hg), and vaporization (hfg = hg - hf) or latent heat of vaporization.
Specific entropy of saturated liquid (sf), saturated vapor (sg), and vaporization (sfg = sg - sf)
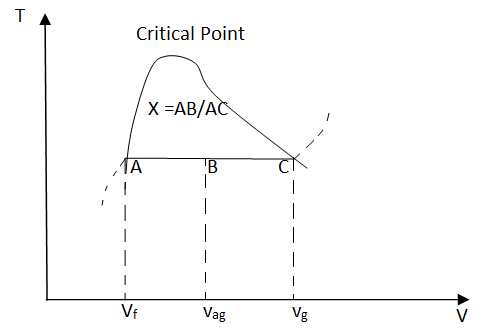
Saturated Mixture
During the vaporization process of water, the substance is a mixture of saturated liquid and saturated vapor. Quality (x) is defined to describe the fraction of saturated vapor in the mixture. x = mvapor/mtotal Quality has a value between 0 and 1. x equals 1 for saturated vapor and x equals 0 for saturated liquid according to its definition. Saturated mixture is a two-phase system. For convenience, it can be treated as a homogenous mixture and the properties of this mixture are simply the average properties of the saturated liquid and saturated vapor. For example, the specific volume of the mixture can be determined by Vav = Vf + Vg mtotal vav = mf vf + mg vg Rearranging the above equation to give an expression for the quality x as x = (vav - vf)/vfg Based on this equation, quality can be determined from the horizontal distance on the T-v or P-v diagram as shown in the figure.
The above process can be repeated for u and h uav = uf + ufg x hav = hf + hfg x Superheated Vapor
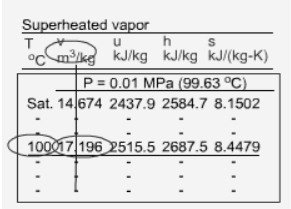
Since the superheated vapor is a single phase substance, the temperature and pressure are independent. In the superheated vapor tables, the properties are listed as a function of both the temperature and pressure. The tabulated properties include v, u, h and s. The saturation temperature corresponding to the pressure is given in the parentheses following the pressure value. Superheated vapor can be characterized by
h > hg at a given P or T Sub cooled Liquid
The format of the sub cooled liquid water tables is similar to the format of the superheated vapor tables. In the absence of compressed liquid data, a common practice is to use the saturated liquid data based on the given temperature to estimate the properties of compressed liquid. For h, the error can be reduced using the following approximation Subcooled liquid can be characterized by
h <hf at a given P or T The entropy of a pure substance is determined from tables in the same manner as other properties such as v, u, and h. The value of entropy at a specified state is determined just like any other property.
If the compressed liquid data are not available, the entropy of the compressed liquid can be approximated by the saturated liquid at the same temperature. An isentropic process is a thermodynamic process, in which the entropy of the fluid or gas remains constant. It means the isentropic process is a special case of an adiabatic process in which there is no transfer of heat or matter. It is a reversible adiabatic process. An isentropic process can also be called a constant entropy process. In engineering such an idealized process is very useful for comparison with real processes. Since there are changes in internal energy (dU) and changes in system volume (∆V), engineers often use the enthalpy of the system, which is defined as: H = U + pV In many thermodynamic analyses it is convenient to use the enthalpy instead of the internal energy. Especially in case of the first law of thermodynamics
Property Diagram Involving Entropy
Property diagrams serve as great visual aids in the thermodynamic analysis of processes. We have used P-v and T-v diagrams extensively in previous chapters in conjunction with the first law of thermodynamics. In the secondlaw analysis, it is very helpful to plot the processes on diagrams for which one of the coordinates is entropy. The two diagrams commonly used in the second-law analysis are the temperature-entropy and the enthalpy-entropy diagrams. Consider the defining equation of entropy (Eq). It can be rearranged as
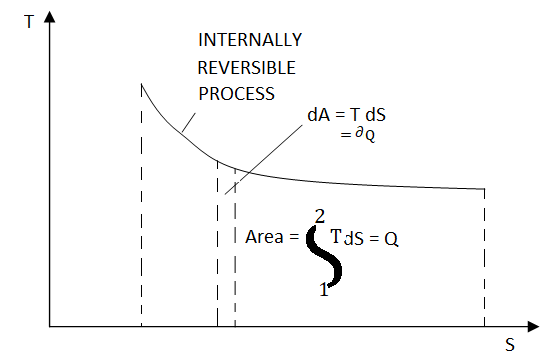
FIGURE 17 On a T-S diagram
the area under the process curve represents the heat transfer for internally reversible processes.
Equation 1as shown in Fig 17dQrev int corresponds to a differential area on a T-S diagram. The total heat transfer during an internally reversible process is determined by integration to be
Equation 2 which corresponds to the area under the process curve on a T-S diagram Therefore, we conclude that the area under the process curve on a T-S diagram represents heat transfer during an internally reversible process. This is somewhat analogous to reversible boundary work being represented bythe area under the process curve on a P-V diagram. Note that the area under the process curve represents heat transfer for processes that are internally (or totally) reversible. The area has no meaning for irreversible processes. Equations 1 and 2 can also be expressed on a unit-mass basis as
To perform the integrations in Equation 2 and 4, one needs to know the relationship between T and s during a process. One special case for which these integrations can be performed easily is the internally reversible isothermal process. It yields
5 or 6 where T0 is the constant temperature and S is the entropy change of the system during the process. An isentropic process on a T-s diagram is easily recognized as a verticalline segment. This is expected since an isentropic process involves no heat transfer, and therefore the area under the process path must be zero (Fig. 18).
FIGURE 18 the isentropic process appears as a vertical line segment on a T-s diagram.
The T-s diagrams serve as valuable tools for visualizing the second-law aspects of processes and cycles, and thus they are frequently used in thermodynamics. The T-s diagram of water is given in the appendix in Fig. A–9. Another diagram commonly used in engineering is the enthalpy-entropy diagram, which is quite valuable in the analysis of steady-flow devices such as turbines, compressors, and nozzles.
FIGURE 19 for adiabatic steady-flow devices
The vertical distance h on an h-s diagram is a measure of work, and the horizontal distance s is a measure of irreversibilities.
The coordinates of an h-s diagram represent two properties of major interest: enthalpy, which is a primary property in the first-law analysis of the steady-flow devices, and entropy, which is the property that accounts for irreversibilities during adiabatic processes. In analysing the steady flow of steam through an adiabatic turbine, for example, the vertical distance between the inlet and the exit states h is a measure of the work output of the turbine, and the horizontal distance s is a measure of the irreversibilities associated with the process (Fig. 7–18). The h-s diagram is also called a Mollier diagram.
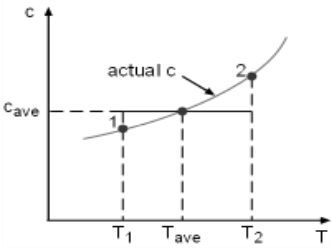
Entropy Change of Solids and Liquids For incompressible substances, the specific volume does not change during a process. That is, dv = 0
The internal energy of an incompressible substance is du = c(T) dT Most solids and liquids can be approximated as incompressible substances. The entropy change of solids and liquids can be obtained by applying the above two equations to the first Tds equation. The entropy change during a process 1-2 is If the temperature variation (T2 - T1) is small over the entire process, an average specific heat (cave) is used and treated as a constant (constant-specific-heats assumption). Then the entropy change can be evaluated by The entropy change of ideal gases The property relations for ideal gases are: pv = RT The first relation of entropy change for ideal gases is obtained by replacing P by RT/v and du by cvdT in the first Tds equation: Tds = du + Pdv ds = cvdT/T + Rdv/v Integrating ds from state 1 to state 2 gives the first relation of entropy change for ideal gases. The second relation of entropy change for ideal gases is obtained by replacing v by RT/P and dh by cPdT in the second Tds equation: Tds = dh - vdP ds = cPdT/T - RdP/P Integrating ds from state 1 to state 2 gives the second relation of entropy change for ideal gases A common approximation is made by assuming that the specific heats of ideal gases are constants if the temperature variation is small (constant-specific-heats assumption). Replacing cv and cP with constants cv,av and cP,av in the first and second relations of entropy change and integrating from state 1 to state 2 gives,
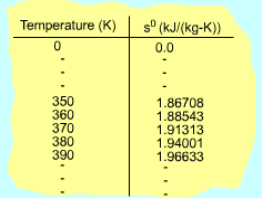
Fig 21 Function s0 is a Function ofTemperature only
If the temperature variation is large, the variation of specific heats with temperature should be considered and relations between cv(T), cP(T) and temperature are needed to integrate the first and second relations. For convenience, a function s0, standard-state entropy, is defined as s0 is a function of temperature only and is tabulated with temperature. Absolute zero is used as the reference temperature. Replacing T as T1 and T2 in the above definition gives Then the entropy change of ideal gases during a process 1-2 is
|
Key takeaways
- mtotal = mliquid + mvapor = mf + mg
- Standard-state entropy, is defined as
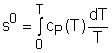
Reversible steady-flow work The energy balance for a steady-flow device (nozzle, compressor, turbine and pump) with one inlet and one exit is: Its differential form is: δq - δw = dh + dke + dpe If the device undergoes an internally reversible process, the heat transfer term δq can be replaced by dh - vdP since δqrev = Tds Tds = dh - vdP (the second Tds relation) Then the energy balance becomes dh - vdP - δwrev = dh + dke + dpe By rearranging the above equation, the reversible steady-flow work can be expressed as - δwrev = vdP + dke + dpe Integrating it form location 1 to location 2 yields,
The above equation is the relation for the reversible work output associated with an internally reversible process in a steady-flow device. When the changes in kinetic and potential energies are negligible, the relation reduces to The above equation states that the larger the specific volume, the larger the reversible work produced or consumed by a steady-flow device. To minimize the work input during a compression process, one should keep the specific volume of the working fluid as small as possible. In the same manner, to maximize the work output during an expansion process, one should keep the specific volume of the working fluid as large as possible.
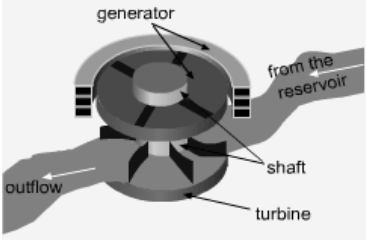
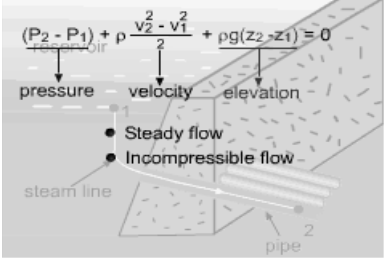
One needs to know the relationship between the specific volume v and the pressure P for the given process to perform the integration in the above relation. If an incompressible fluid is used as the working fluid, the specific volume v is a constant. The relation for the reversible work output associated with an internally reversible process in a steady-flow device is simplified to give wrev = -v(P2 - P1) - Δke - Δpe Hydraulic turbines used in hydroelectric power plants run in a steady-flow process with incompressible fluid, i.e., water, as the working fluid
If no work interactions are involved, like nozzle or pipe section, the above equation is reduced to
Reversible Steady-flow Devices produce Most and Consume Least Work The steady-flow devices deliver the most and consume the least work when it undergoes a reversible process. Consider two steady-flow devices, one is reversible and the other is irreversible (actual process), operating between the same inlet and exit states. The differential forms for the energy balance of these two devices are δqact - δwact = dh + dke + dpe δqrev - δwrev = dh + dke + dpe The right hand sides of these two equations are the same. It gives, qact - δwact = qrev - δwrev Rearranging this equation gives, δwrev - δwact = qrev - qact Since qrev = Tds, the above equation becomes, δwrev - δwact = Tds - qact the increase of entropy principle gives Thus, δwrev - δwact
That is, for the same inlet and exit conditions, when the device undergoes a reversible process, a work-produce device like turbine produces the most work (w is positive), or a work-consuming device like compressor consumes the least work (w is negative)
|
|
Fig 27
The isentropic process
• involves no irreversibilities and serves as the ideal process for adiabatic
devices
• The ideal process that can serve as a suitable model for adiabatic steady-flow
devices (e.g. turbine, compressors, nozzle)
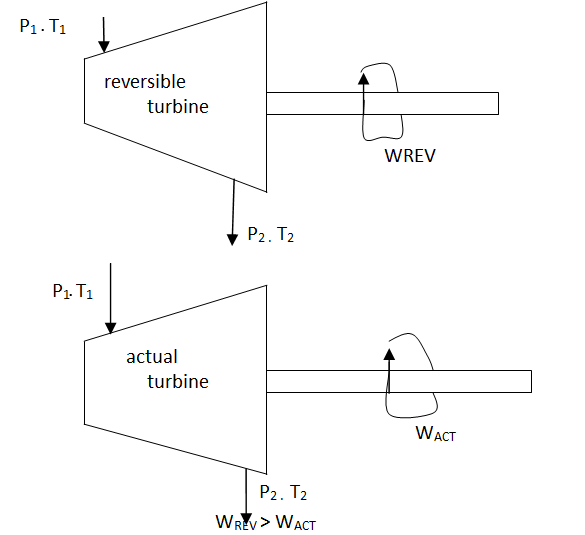
Isentropic Efficiencies of Turbines
The ratio of the actual work output of the turbine to the work output that would be achieved if the process between the inlet state and the exit pressure were isentropic
|
Fig 28
η = Actual turbine work / Isentropic turbine work = wa/ws
h1-h2a / h1-h2s
∆ke<<∆h
∆pe<<∆h
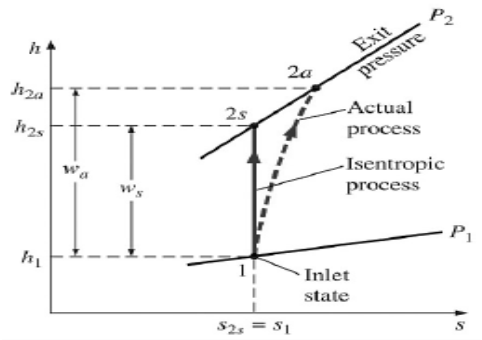
Isentropic Efficiencies of Compressors and Pumps
The ratio of the work input required to raise the pressure of a gas to a specified value in an isentropic manner to the actual work input
Fig 29
A realistic model process for compressors that are intentionally cooled during the compression process is the reversible isothermal process, defined as isothermal Efficiency c = wt/ wa
|
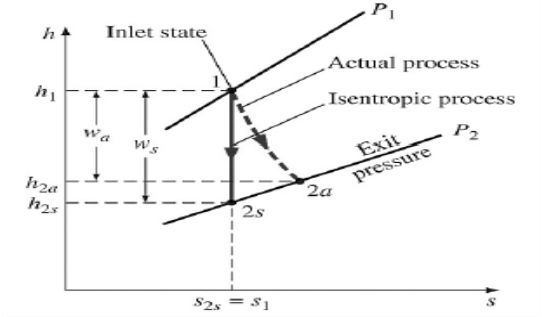
Isentropic Efficiencies of Nozzles
The ratio of the actual kinetic energy of the fluid at the nozzle exit to the kinetic energy value at the exit of an isentropic nozzle of the same inlet state and exit pressure
|
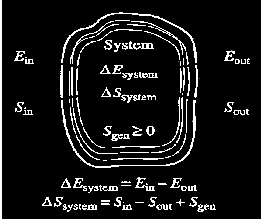
Entropy Balance
Increase of entropy principle for any system (Total entropy entering) – (total entropy leaving) + (total entropy generated) = (change in the total entropy of the system)
Fig 31
the entropy change of a system during a process is equalto the net entropy transfer through the system boundaryand the entropy generated within the system Entropy change of the system
|
Energy is a measurement of the ability of something to do work. It is not a material substance. Energy can be stored and measured in many forms.
Although we often hear people talking about energy consumption, energy is never really destroyed. It is just transferred from one form to another, doing work in the process. Some forms of energy are less useful to us than others for example, low level heat energy. It is better to talk about the consumption or extraction of energy resources, for example coal, oil, or wind, than consumption of energy itself.
- A speeding bullet has a measurable amount of energy associated with it; this is known as kinetic energy. The bullet gained this energy because work was done on it by a charge of gunpowder which lost some chemical potential energy in the process.
- A hot cup of coffee has a measurable amount of thermal energy which it acquired via work done by a microwave oven, which in turn took electrical energy from the electrical grid.
In practice, whenever work is done to move energy from one form to another, there is always some loss to other forms of energy such as heat and sound. For example, a traditional light bulb is only about 3% efficient at converting electrical energy to visible light, while a human being is about 25% efficient at converting chemical energy from food into work.
The standard unit used to measure energy and work done in physics is the joule, which has the symbol J. In mechanics, 1 joule is the energy transferred when a force of 1 Newton is applied to an object and moves it through a distance of 1 meter.
Another unit of energy you may have come across is the Calorie. The amount of energy in an item of food is often written in Calories on the back of the packet. A typical 60 gram chocolate bar for example contains about 280 Calories of energy. One Calorie is the amount of energy required to raise 1 kg of water by 10degrees Celsius. This is equal to 4184 joules per Calorie, so one chocolate bar has 1.17 million joules or 1.17 MJ of stored energy.
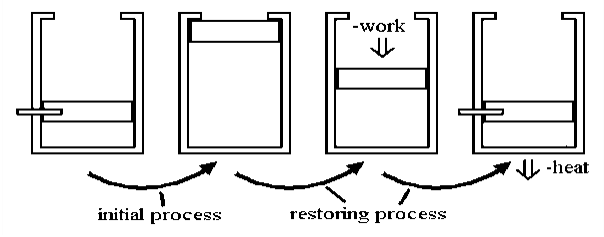
Reversible work (Wrev) is the maximum amount of Useful work (Wu) that can be produced (or the minimum amount of Wu that needs to be supplied) as a system undergoes a process between specified initial and final states.
Fig 32 From situation 1, we can deduce that for constant-volume processes, the total work is equal to the useful work, i.e. W = Wu (as the V2-V1 term in Wsurr is 0) Situation example 1: Finding Wu for the expansion of a closed system:
Irreversibility (I) The Irreversibility (I) of a process is the difference between Wrev and Wu. It is also equal to the Exergy destroyed. - For a work-producing device: I=Wrev, out - Wu,out - For a work-consuming device: I= Wu, in - Wrev, in I is always a positive quantity since Wrev> Wu for work-producing devices and Wrev< Wu for work-consuming devices. The smaller the irreversibility of a process, the more work can be produced (or less work consumed). Therefore, the performance of a system can be improved by reducing the irreversibility associated with it.
|
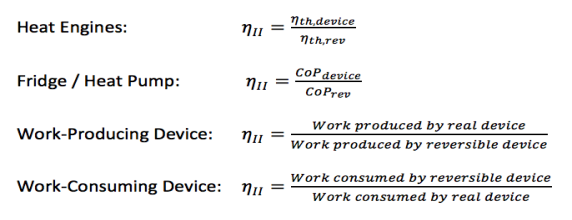
The Second Law of Thermodynamics states that no real process can be completely isentropic. Or, restated in terms of exergy, no real process can use 100% of the exergy within a system.Engineering aims to minimise the generation of entropy. Second-law efficiencies measure how successfully entropy generation has been minimised in a device by comparing real processes to an equivalent idealised isentropic process via their thermal efficiencies or COPs are appropriate:
|
Think of the amount of exergy not used as the energy lost due to the generation of entropy. Engineering aims to maximise the use of exergy. Hence these formulas can be rewritten in terms of exergy:
|
Change in exergy of a closed system
The exergy of a specified mass at a specified state is the useful work that can be produced as the mass undergoes a reversible process from it's specified state to the state of the environment.
Consider the possible contributors to useful work during the process from the specified state to the state of the environment:
- Change in internal energy, dU
- Expansion/compression work, PdV
- Change in entropy, TdS
- Kinetic energy
- Gravitational potential energy
Add these together to find an expression for the total exergy of a closed system: Writing this per unit mass:
Recall that the total energy, e, of a system is comprised of internal, kinetic and gravitational potential energies. Therefore, the total exergy of a closed system (per unit mass) can be written: So, to find the change in exergy of a closed system when it undergoes a process from an initial state to a final state, simply use the final state of the process instead of the state of the environment in the equation above. The result is:
Change in exergy of a flow The total exergy of a flow is given by:
The change in exergy of a flow is given by: Where the properties of the specified state of the mass are e, v, s, and the properties of the state of the environment are e0, P0, v0, T0, s0. The internal, kinetic and gravitational potential energies have been absorbed into the e terms.the "initial state" in this case is the same as the "specified state" of the "mass" from the definition of exergy, so no change is required. Also note that the environmental pressure and temperature remain in the equation. Where the properties of the initial state are e1, v1, s1, the properties of the final state are e2, v2, s2, and the environmental pressure and temperature is P0 and T0 respectively.Flow exergy per unit mass is represented by lowercase Psi (Greek alphabet)
|
Energy can be transferred to or from a closed system (a fixed mass) in two distinct forms: heat and work. For control volumes, energy can also be transferred by mass. An energy transfer to or from a closed system is heat if it is caused by a temperature difference between the system and its surroundings. Otherwise it is work, and it is caused by force acting through a distance
Energy is transferred to or from a system by three forms: heat, work and mass flow. For a closed system, the only two forms are heat and work since no mass crosses its boundaries.
|
Fig 33 Modes of Heat Transfer
1. Heat transfer (Q)
Heat transfer is the energy interaction caused by a temperature difference between a system and its surroundings. Heat transfer to a system (heat gain) will cause the internal energy of the system to increase, and heat transfer from a system (heat loss) will cause the internal energy of the system to decrease
2. Work (W)
The energy interaction that is not caused by a temperature difference between a system and its surroundings is work. Work transferred to a system will increase the energy of the system, and work transferred from a system will decrease the energy of the system.
3. Mass flow
When mass enters a system, the energy of the system increases because of the energy accompanied by mass. Also the energy of the system decreases when mass leaves the system Heat and work have been introduced in the previous sections. Systems that involve energy balance with mass flow are considered in the following section.
|
Fig 34 Some Forms of Work
Note that net transfer of a quantity is equal to the difference between the amounts transferred in and out, the energy balance can be written as:
(Qin - Qout) + (Win - Wout) + (Emass,in - Emass,out) = ΔEsystem |
All the quantities of the six terms in the left are positive amounts since the direction of the energy transfer is described by the subscripts "in" and "out.
The Decrease of Exergy Principle The decrease of Exergy principle is the counterpart of the increase of Exergy principle. By definition, no heat, work, or mass can cross the boundaries of an isolated system, meaning there is no energy and entropy transfer. As a result, the energy and entropy balances for an isolated system can be expressed as - Energy Balance: Ein - Eout = ΔEsystem→ 0 = E2 - E1 0↗ 0↗ Entropy balance: Sin - Sout+ Sgen = ΔSsystem→Sgen = S2 - S1 0↗ 0↗ Multiplying the second relation by T0 and subtracting it from the first gives - -T0Sgen = E2 - E1 - T0(S2 - S1) Additionally, we know that - X2 - X1 = (E2 - E1) + P0(V2 - V1) - T0(S2 - S1) 0↗ = E2 - E1 - T0(S2 - S1) Since V2 = V1 for any isolated system. Combining the previous 2 equations gives -T0Sgen = X2 - X1 ≤ 0 T0 is the thermodynamic temperature of environment, and is therefore a positive quantity. Sgen ≤ 0 meaning T0Sgen ≤ 0from this it can be seen that – ΔXisolated = (X2 - X1)isolated≤ 0 This equation that during a process in an isolated systemExergy always decreases, unless the process is perfectly reversible in which case it remains constant. No process can ever be truly reversible however meaning for an isolated system exergy is always destroyed during a process. Exergy Destruction All irreversible processes result in entropy being generated. Using the equation below, it can be seen that the exergy destroyed is proportional to the entropy generated Xdestroyed = T0Sgen ≥ 0
|
Any process can be thought of as taking place in an isolated system, and therefore this equation can be applied to any process. Exergy destroyed represents the lost work potential and can be known as irreversibility or lost work. If the exergy destroyed takes a positive value, the process is feasible but irreversible, if it is 0, the process is perfectly reversible and if it is negative, meaning exergy is generated during the process, then the process is not feasible or reversible. No process is truly reversible, and therefore any actual process has a positive value for exergy destroyed, which means that the exergy in the universe is constantly decreasing in the same way the entropy is increasing.
In a closed system the mass is always constant and In an open system (control volume) we need to consider mass balance
(Sum of the rate of mass flowing into the control volume)-(Sum of the rate of mass flowing from the control volume)=(Time rate of change of the mass inside the control volume).
|
Reference:
- Engineering thermodynamics
- ASHRAE, Air Conditioning System Design Manual, IInd edition, ASHRAE.
- Thermodynamics P.K Nag
- Threlkeld J.L., Thermal Environmental Engineering, Prentice Hall Inc. New Delhi
