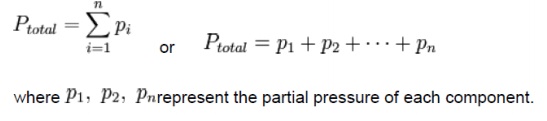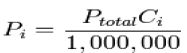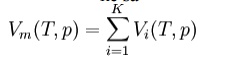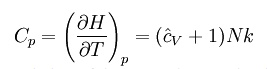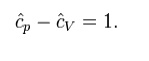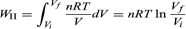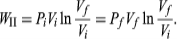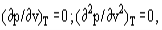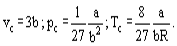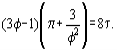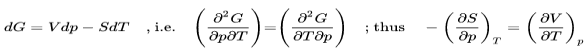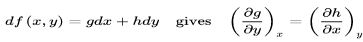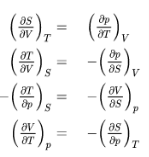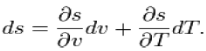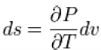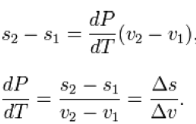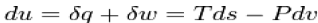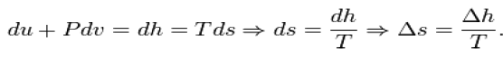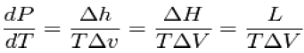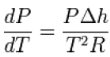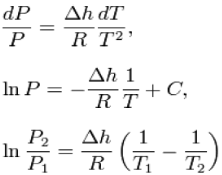Unit - 6
Ideal and Real Gases and Thermodynamic Relations
An ideal gas is defined as a gas whose molecules are spaced far apart so that the behaviour of a molecule is not influenced by the presence of other molecules—a situation encountered at low densities. We also mentioned that real gases approximate this behaviour closely when they are at a low pressure or high temperature relative to their critical-point values. The P-v-T behaviour of an ideal gas is expressed by the simple relation Pv _ RT, which is called the ideal-gas equation of state. The P-v-T behaviour of real gases is expressed by more complex equations of state or by Pv _ ZRT, where Z is the compressibility factor.
When two or more ideal gases are mixed, the behavior of a molecule normally is not influenced by the presence of other similar or dissimilar molecules, and therefore a non-reacting mixture of ideal gases also behaves as an ideal gas. Air, for example, is conveniently treated as an ideal gas in the range where nitrogen and oxygen behave as ideal gases. When a gas mixture consists of real (non-ideal) gases, however, the prediction of the P-v-T behavior of the mixture becomes rather involved.
The prediction of the P-v-T behavior of gas mixtures is usually based on two
models: Dalton’s law of additive pressures
Both models are described and discussed below.
Dalton’s law of additive pressures:
Dalton's law (also called Dalton's law of partial pressures) states that the total pressure exerted by a gaseous mixture is equal to the sum of the partial pressures of each individual component in a gas mixture. This empirical law was observed by John Dalton in 1801 and is related to the ideal gas laws. Mathematically, the pressure of a mixture of gases can be defined as the summation
It is assumed that the gases do not react with each other.
Where xi is the mole fraction of the i-th component in the total mixture of m components The relationship below provides a way to determine the volume based concentration of any individual gaseous component.
Where Ci is the concentration of the ith component expressed in ppm Dalton's law is not exactly followed by real gases. Those deviations are considerably large at high pressures. In such conditions, the volume occupied by the molecules can become significant compared to the free space between them. Moreover, the short average distance between molecules raises the intensity of intermolecular forces between gas molecules enough to substantially change the pressure exerted by them. Neither of those effects is considered by the ideal gas model.
|
Amagat’s law of additive volumes:
Amagat's law or the Law of Partial Volumes of 1880 describes the behavior and properties of mixtures of ideal (as well as some cases of non-ideal) gases. Of use in chemistry and thermodynamics, Amagat's law states that the volume Vm of a gas mixture is equal to the sum of volumes Vi of the K component gases, if the temperature T and the pressure p remain the same:
|
This is the experimental expression of volume as an extensive quantity. It is named after Emile Amagat. Both Amagat's and Dalton's Law predict the properties of gas mixtures. Their predictions are the same for ideal gases. However, for real (non-ideal) gases, the results differ. Dalton's Law of Partial Pressures assumes that the gases in the mixture are non-interacting (with each other) and each gas independently applies its own pressure, the sum of which is the total pressure. Amagat's Law assumes that the volumes of each component gas (same temperature and pressure) are additive; the interactions of the different gases are the same as the average interactions of the components.
Heat capacity
The heat capacity at constant volume of an ideal gas is:
It is seen that the constant is just the dimensionless heat capacity at constant volume. It is equal to half the number of degrees of freedom per particle. Formoderate temperatures, the constant for a monoatomic gas is Cv = 3/2 while for a diatomic gas it Is Cv = 5/2 . It is seen that macroscopic measurements on heat capacity provide information on the microscopic structure of the molecules.
Where H = U + pV is the enthalpy of the gas. It is seen that is also a constant and that the dimensionless heat capacities are related by:
|
Key Takeaways
- The heat capacity at constant volume of an ideal gas is:
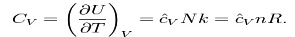
2. H = U + pV is the enthalpy of the gas
Equation of state
The equation of state for a substance provides the additional information required to calculate the amount of work that the substance does in making a transition from one equilibrium state to another along some specified path. The equation of state is expressed as a functional relationship connecting the various parameters needed to specify the state of the system. The basic concepts apply to all thermodynamic systems, but here, in order to make the discussion specific, a simple gas inside a cylinder with a movable piston will be considered. The equation of state then takes the form of an equation relating P, V, and T, such that if any two are specified, the third is determined. In the limit of low pressures and high temperatures, where the molecules of the gas move almost independently of one another, all gases obey an equation of state known as the ideal gas law: PV = nRT, where n is the number of moles of the gas and R is the universal gas constant, 8.3145 joules per K. In the International System of Units, energy is measured in joules, volume in cubic metres (m3), force in newtons (N), and pressure in pascals (Pa), where 1 Pa = 1 N/m2. A force of one newton moving through a distance of one metre does one joule of work. Thus, both the products PV and RT have the dimensions of work (energy). A P-V diagram would show the equation of state in graphical form for several different temperatures.
To illustrate the path-dependence of the work done, consider three processes connecting the same initial and final states. The temperature is the same for both states, but, in going from state i to state f, the gas expands from Vi to Vf (doing work), and the pressure falls from Pi to Pf. According to the definition of the integral in equation, the work done is the area under the curve (or straight line) for each of the three processes. For processes I and III the areas are rectangles, and so the work done is WI = Pi(Vf − Vi) and WIII = Pf(Vf − Vi) respectively.
Process II is more complicated because P changes continuously as V changes. However, T remains constant, and so one can use the equation of state to substitute P = nRT/V in above equation to obtain
|
WII is thus the work done in the reversible isothermal expansion of an ideal gas. The amount of work is clearly different in each of the three cases. For a cyclic process the net work done equals the area enclosed by the complete cycle.
Avogadro’s Law
Avogadro’s law, a statement that under the same conditions of temperature and pressure equal volumes of different gases contain an equal number of moleculesThis empirical relation can be derived from the kinetic theory of gases under the assumption of a perfect (ideal) gas. The law is approximately valid for real gases at sufficiently low pressures and high temperatures.
The specific number of molecules in one gram-mole of a substance, defined as the molecular weight in grams, is 6.02214076 × 1023, a quantity called Avogadro’s number, or the Avogadro constant. For example, the molecular weight of oxygen is 32.00, so that one gram-mole of oxygen has a mass of 32.00 grams and contains 6.02214076 × 1023 molecules.
The volume occupied by one gram-mole of gas is about 22.4 litres (0.791 cubic foot) at standard temperature and pressure (0 °C, 1 atmosphere) and is the same for all gases, according to Avogadro’s law.
Vander Waal’s equation of state
The equation of state of the perfect gas refers to a gas consisting of point like items which do not interact with one another instead of this van der Waals proposed an equation

Where a and b are the so-called van der Waals constants and which have different values for each gas.The b correction takes into account the fact that, according to van der Waals. The real gas molecules can move not in the total volume occupied by the gas, but only in a part of this volume which is defined by subtracting what he called the molecules own volume.
The correction a/ν2 proportional to the square of density-takes into account the attraction forces existing between gas molecules. According to the van der Waals assumption, these forces decrease the pressure against the vessel walls, because the molecules which are close to the wall are subjected to attraction of other molecules the a and b constants are to be considered as empirical; they have to be derived from experimental data on the density, temperature and pressure interdependence. For a number of technically important gases the van der Waals constants are tabulated.
According to the method of allowing for deviation of a real gas from a perfect gas, the van der Waals equation supposedly would be valid only for small deviations, i.e., for moderate pressures. But it turned out that this equation qualitatively satisfactorily describes the real gases behaviour in a wide range of parameters including the critical region.
The van der Waals equation is a cubic one with respect to the specific volume. This means that in general at a given temperature, each pressure value corresponds to three specific volume values v1, v, v2. The values ν1 and ν2 correspond to physically existing states of liquid and vapor. The value ν, where (∂p/∂v)T >0 corresponds to an unstable state and does not exist physically
As the temperature increases, the values ν1 and ν2 get closer and finally at the critical point all three roots coincide at the critical volume νc. At higher temperatures only one root of the van der Waals equation remains real, the two other being imaginary. These supercritical isotherms reveal inflexions at ν = νc which is close to the behaviour of real substances.
As far as at the critical point, the following conditions are valid:
and it is possible, using the van der Waals equation, to derive interconnections between the van der Waals constants and critical parameters of a substance.
Hence the critical compressibility factor Zc will be identical for all substances and equal to
In reality the critical compressibility factors for the most substances fit into range 0.21-0.31.
The van der Waals equation can be rearranged to a non-dimensional form using the reduced parameters:
In this coordinates the van der Waals equation becomes:
This means that, with reduced parameters, all substances obeying the van der Waals equation are described by an identical equation of state. From here it follows that all these substances can be treated similarly. For instance, at identical π and τ all substances have the same φ values. This generalized approach is used also with more sophisticated equations of state which describe the real substances behaviour better than the van der Waals equation
|
Compressibility factor
Compressibility factor also known as the gas deviation factor or the compression factor is a measure of deviations in the thermodynamic property of a real gas from ideal gas behaviour. In simple words, we can say that it is a correction factor that best describes the amount of gas that deviates from its perfect behaviour at a certain temperature and pressure. Normally, it is used to modify the law of ideal gas.
Compressibility Factor is also often defined as “the ratio of molar volume of gas to that of an ideal gas.” It is expressed as Z = pV / RT.
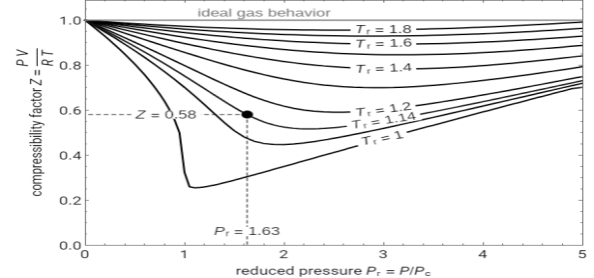
Compressibility chart
The compressibility factor chart plots the compressibility factor Z, equal to PV/RT, where V is the volume per mole, versus the reduced pressure Pr for several values of the reduced temperature Tr. The reduced pressure and temperature are defined by Pr = P/PC and Tr = T/TC, respectively, where PC is the critical pressure and TC is the critical temperature. Use buttons to select one of five molecules, and move the black dot to display the compressibility factor curve (blue) for any value of Tr between 1.0 and 1.8. The Z and Pr values for the location of the black dot are displayed on the chart. For an ideal gas, Z = 1 (green line).
|
Fig 1
Key takeaways
- Compressibility Factor is also often defined as “the ratio of molar volume of gas to that of an ideal gas.” It is expressed as Z = pV / RT.
- van der Waals proposed an equation
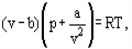
3. The specific number of molecules in one gram-mole of a substance, defined as the molecular weight in grams, is 6.02214076 × 1023, a quantity called Avogadro’s number, or the Avogadro constant.
The pressure exerted by an individual gas in a mixture is known as its partial pressure.
Assuming we have a mixture of ideal gases, we can use the ideal gas law to solve problems involving gases in a mixture.
Dalton's law of partial pressures states that the total pressure of a mixture of gases is equal to the sum of the partial pressures of the component gases:
PTotal=Pgas 1+Pgas 2+Pgas 3….
Dalton's law can also be expressed using the mole fraction of a gas, x:
Pgas 1=x1PTotal
Dalton's law of partial pressures
Dalton's law of partial pressures states that the total pressure of a mixture of gases is the sum of the partial pressures of its components:
PTotal=Pgas 1+Pgas 2+Pgas 3….
Where the partial pressure of each gas is the pressure that the gas would exert if it was the only gas in the container that is because we assume there are no attractive forces between the gases.
|
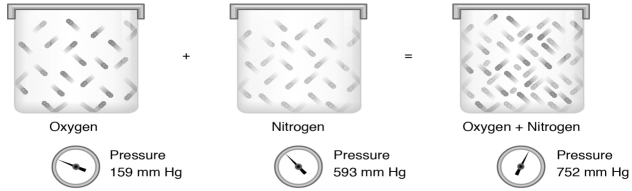
Fig 2
From left to right: A container with oxygen gas at 159 mm Hg, plus an identically sized container with nitrogen gas at 593 mm Hg combined will give the same container with a mixture of both gases and a total pressure of 752 mm Hg.
The partial pressure of a gas in a mixture is the same as the pressure of the gas in the container by itself. The sum of the partial pressures gives the total pressure of the gas mixture.
Dalton's law of partial pressure can also be expressed in terms of the mole fraction of a gas in the mixture. The mole fraction of a gas is the number of moles of that gas divided by the total moles of gas in the mixture, and it is often abbreviated as x:
x1=mole fraction of gas 1= moles of gas 1/total moles of gas
Dalton's law can be rearranged to give the partial pressure of gas 1 in a mixture in terms of the mole fraction of gas 1:
Pgas 1=x1PTotal
Both forms of Dalton's law are extremely useful in solving different kinds of problems including:
- Calculating the partial pressure of a gas when you know the mole ratio and total pressure
- Calculating moles of an individual gas if you know the partial pressure and total pressure
- Calculating the total pressure if you know the partial pressures of the components
Exact differentials
It is usual to formulate the basic equations of thermodynamics in terms of differentials. The conservation of energy is written as
dU=dQ−dW
Where dU, dQ, and dW are the differentials of the internal energy, the heat absorbed and the work performed by a system The conservation of energy is expressed by equation as long as dU is an exact differential, a key feature that is not explicitly stated but is tacitly understood. An exact differential such as dU means that there exists a state function U such that its differential is dUan inexact differential such as dQ and dW, does not hold this property. It should be pointed out that some authors use a distinction notation to refer does to an inexact differential. One of them is to cross the differential, a procedure that becomes quite confusing and useless.
The differential of the work dW is written in terms of exact differential. In the case of mechanical work, for instance, dW=pdV where p is the pressure and dV is the differential of the volume V. In an analogous way the differential of heat can also be written in terms of an exact differential. If a system is in thermodynamic equilibrium than dQ/T is the exact differential dS of the entropy S This result allows us to write the relation dQ=TdS between heat and entropy, which should be understood as valid as long as the system is in thermodynamic equilibrium.
Differentials appeared with the invention of calculus in the second half of the seventeenth century. The differential dx was understood as a small increment of the variable x. If another variable y depends on the independent variable x, then the resulting increment dy of y is its differential. The quotient of these two differentials, dy/dx, was interpreted geometrically by Leibniz as the ratio of the ordinate y of a point on a curve and the length of the sub tangent associated to this point.
The formulation of thermodynamics in terms of differentials seemed to be a natural consequence of the application of differential calculus at the time of the emergence of thermodynamics around the middle of the eighteenth century. Clausius formulated the laws of thermodynamics by the use of differentials. The same can be said about the development of mechanics in the eighteenth century, particularly the formulation of analytical mechanics by Lagrange.
Here, we give an account and an analysis of the development of the concept of differential and its application during the early development of mechanics and thermodynamics. Our presentation starts with the introduction of the differential and integral calculus by Newton and Leibniz. Then we analyse the developments of the basic rules of differential calculus and the concepts of integrating factor, exact and inexact differentials. Next we show how the application of differential calculus was used to solve mechanical problems such as the brachistochone problem. In the second part, we analyze how the differentials were used by Lagrange in his analytical mechanics and by Clausius in his development of thermodynamics.
T-D relations, Maxwell relations
The fundamental equations represent exact differentials, e.g.
Generally
So from the other fundamental equations we get further Maxwell relations:
These Maxwell relations allow for drastic simplification and replacements of difficult-to-measure relations by easy-to-measure relations and thus contribute strongly to the powerful toolbox of thermodynamics as we will see in some subsequent examples.
|
Key takeaways
- The conservation of energy is written as
dU=dQ−dW
2. Maxwell relations:
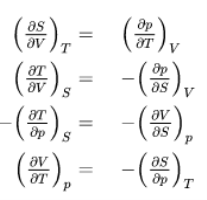
The Clausius–Clapeyron relation, who defined it sometime after 1834, is a way of characterizing the phase transition between two phases of matter, such as solid and liquid. On a pressure– temperature (P–T) diagram, the line separating the two phases is known as the coexistence curve. The Clausius–Clapeyron relation gives the slope of this curve.
Mathematically,
dP/dT = L /T∆V
Where dP/ dTis the slope of the coexistence curve, L is the latent heat, T is the
Temperature and ΔV is the volume change of the phase transition.
The generalized equation given in the opening of this article is sometimes called
theClapeyron equation, while a less general form is sometimes called the Clausius– Clapeyron equation. The less general form neglects the magnitude of the specific volume of the liquid (or solid) state relative to that of the gas state and also approximates the specific volume of the gas state via the ideal gas law.
Pressure Temperature Relations
|
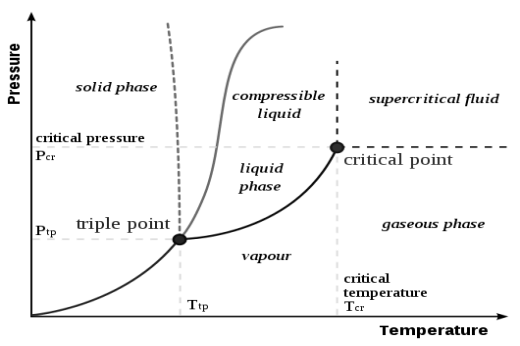
Fig 3 A typical phase diagram
The dotted line gives the anomalous behavior of water. The Clausius–Clapeyron relation can be used to (numerically) find the relationships between pressure and temperature for the phase change boundaries. Entropy and volume changes (due to phase change) are orthogonal to the plane of this drawing
Derivation
Using the state postulate, take the specific entropy, s, for a homogeneous Substance to be a function of specific volume, v, and temperature, T
During a phase change, the temperature is constant,
Sousing theappropriate Maxwell relation gives
Since temperature and pressure are constant during a phase change, thederivative of pressure with respect to temperature is not a function of the specific volume. Thus the partial derivative may be changed into a total derivative and be factored out when taking an integral from one phase to another,
Δ is used as an operator to represent the change in the variable that follows it—final (2) minus initial (1) For a closed system undergoing an internally reversible process, the first law is
Using the definition of specific enthalpy, h, and the fact that the temperature and Pressure are constant, we have
After substitution of this result into the derivative of the pressure, one finds
Where the shift to capital letters indicates a shift to extensive variables this last equation is called the Clausius–Clapeyron equation, though some thermodynamics texts just call it the Clapeyron equation, possibly to distinguish it from the approximation below.
When the transition is to a gas phase, the final specific volume can be many times the size of the initial specific volume. A natural approximation would be to replace Δvwithv2. Furthermore, at low pressures, the gas phase may be approximated by the ideal gas law so that v2 = vgas = RT / P, where R is the mass specific gas constant (forcing h and v to be mass specific). Thus,
This leads to a version of the Clausius–Clapeyron equation that is simpler to integrate:
C is a constant of integration.
These last equations are useful because they relate saturation pressure and saturation temperature to the enthalpy of phase change, without requiring specific volume data. Note that in this last equation, the subscripts 1 and 2 correspond to different locations on the pressure versus temperature phase lines. In earlier equations, they corresponded to different specific volumes and entropies at the same saturation pressure and temperature.
|
Joule – Thomson coefficient
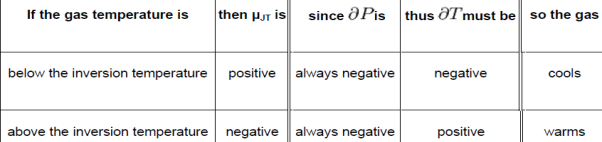
The rate of change of temperature T with respect to pressure P in a Joule–Thomson process (that is, at constant enthalpy H) is the Joule–Thomson (Kelvin) coefficient μJT. This coefficient can be expressed in terms of the gas's volume V, its heat capacity at constant pressure Cp, and its coefficient of thermal expansion α as
The value of μJTis typically expressed in °C/bar (SI units: K/Pa) and depends on the type of gas and on the temperature and pressure of the gas before expansion. All real gases have an inversion point at which the value of μJT changes sign.
The temperature of this point, the Joule–Thomson inversion temperature, depends on the pressure of the gas before expansion.
In a gas expansion the pressure decreases, so the sign of ∂P is always negative. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:
Helium and hydrogen are two gases whose Joule–Thomson inversion temperatures at a pressure of one atmosphere are very low (e.g., about 51 K (−222 °C)for helium). Thus, helium and hydrogen warm up when expanded at constant enthalpy at typical room temperatures. On the other hand nitrogen and oxygen, the two most abundant gases in air, have inversion temperatures of 621 K (348 °C) and 764 K (491 °C) respectively: these gases can be cooled from room temperature by the Joule– Thomson effect. For an ideal gas, μJT is always equal to zero: ideal gases neither warm nor cool upon being expanded at constant enthalpy.
|
Applications
In practice, the Joule–Thomson effect is achieved by allowing the gas to expand
Through a throttling device (usually a valve) which must be very well insulated to prevent any heat transfer to or from the gas. No external work is extracted from the gas during the expansion (the gas must not be expanded through a turbine, for example).
The effect is applied in the Linde technique as a standard process in the petrochemical industry, where the cooling effect is used to liquefy gases, and also in many cryogenic applications (e.g. for the production of liquid oxygen, nitrogen, and argon). Only when the Joule–Thomson coefficient for the given gas at the given temperature is greater than zero can the gas be liquefied at that temperature by the Linde cycle. In other words, a gas must be below its inversion temperature to be liquefied by the Linde cycle. For this reason, simple Linde cycle liquefiers cannot normally be used to liquefy helium, hydrogen, or neon.
Key takeaways
- The Clausius–Clapeyron relation gives the slope of this curve.
dP/dT = L /T∆V
Reference:
- Engineering thermodynamics
- ASHRAE, Air Conditioning System Design Manual, IInd edition, ASHRAE.
- Thermodynamics P.k nag
- Threlkeld J.L., Thermal Environmental Engineering, Prentice Hall Inc. New Delhi