MODULE 3

Planning and design process

3.1 Planning and Design Process

The aim of design is the achievement of an acceptable probability that structures being designed will perform satisfactorily during their intended life. With an appropriate degree of safety, they should sustain all the loads and deformations of normal construction and use and have adequate durability and adequate resistance to the effects of misuse and fire. Design, including design for durability, construction and use in service should be considered as a whole. The realization of design objectives requires compliance with clearly defined standards for materials, production, workmanship and also maintenance and use of structure in service.

3.2 Material

Reinforced concrete, as a composite material, has occupied a special place in the modern construction of different types of structures due to its several advantages. Due to its flexibilit y in form and superiority in performance, it has replaced, to a large extent, the earlier materials like stone, timber and steel. Further, architect's scope and imaginations have widened to a great extent due to its mouldability and monolithicity. Thus, it has helped the architects and engineers to build several attractive shell forms and other curved structures.

Loads

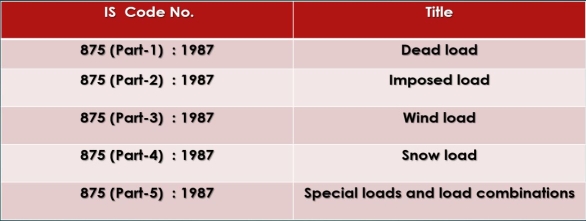
Dead Loads: Dead loads shall be calculated on the basis of unit weights which shall be established taking into consideration the materials specified for. Construction alternatively, the dead loads may be calculated on the basis of unit weights of materials given in IS 875 (Part I). Unless more accurate calculations. The unit weights of plain concrete and reinforced concrete made with sand and· gravel or crushed natural stone aggregate may be taken as 24 kN/m' and 25 kN/m' respectively.

Imposed Loads, Wind Loads and Snow Loads:  Imposed loads, wind loads and snow loads shall be assumed in  accordance with IS 875 (Part 2), IS 875 (Part 3) and IS 875 (Part 4) respectively.

Live Loads:

Live loads on floors and roofs consists of all the loads which are temporarily placed on the structure, For example, loads of people, furniture, machines etc. These loads keep on changing from time to time. They are also called as imposed loads. Various types of imposed loads coming the structure given in IS 875 (Part-2): 1987. The imposed loads depend upon the use of building.

Snow Loads:

The buildings which are located in the regions where snowfall is very common, are to be designed for snow load. The code IS 875 (Part-4): 1987 deals with snow load on roofs of the building.

3.3 Design Safety

3.4 Behavior & Properties of Concrete

Concrete is a product obtained artificially by hardening of the mixture of cement, sand, gravel and water in predetermined proportions The important properties of concrete, which govern the design of concrete mix are as follows

(i) Weight

The unit weights of plain concrete and reinforced concrete made with sand, gravel of crushed natural stone aggregate may be taken as 24 KN/m3 and 25 KN/m3 respectively.

(ii) Compressive Strength

With given properties of aggregate the compressive strength of concrete depends primarily on age, cement content and the water cement ratio are given Table 2 of IS 456:2000. Characteristic strength is based on the strength at 28 days. The strength at 7 days is about two-thirds of that at 28 days with ordinary portland cement and generally good indicator of strength likely to be obtained.

(iii) Increase in strength with age

There is normally gain of strength beyond 28 days. The quantum of increase depends upon the grade and type of cement curing and environmental conditions etc.

(iv) Tensile strength of concrete

The flexure and split tensile strengths of various concrete are given in IS 516:1959 and IS 5816:1970 respectively when the designer wishes to use an estimate of the tensile strength from compressive strength, the following formula can be used

Flexural strength, fcr=0.7√fck N/mm2 (v) Elastic Deformation

The modulus of elasticity is primarily influenced by the elastic properties of the aggregate and to lesser extent on the conditions of curing and age of the concrete, the mix proportions and the type of cement. The modulus of elasticity is normally related to the compressive characteristic strength of concrete

Ec=5000√fck N/mm2

Where Ec= the short-term static modulus of elasticity in N/mm2

fck=characteristic cube strength of concrete in N/mm2

(vi) Shrinkage of concrete

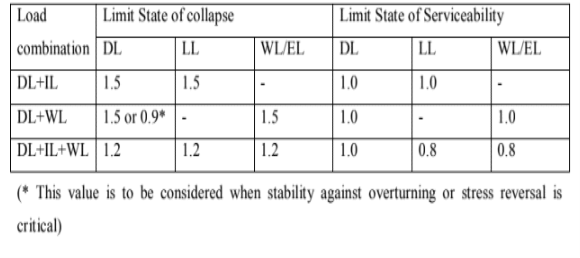
Shrinkage is the time dependent deformation, generally compressive in nature. The constituents of concrete, size of the member and environmental conditions are the factors on which the total shrinkage of concrete depends. However, the total shrinkage of concrete is most influenced by the total amount of water present in the concrete at the time of mixing for a given humidity and temperature. The cement content, however, influences the total shrinkage of concrete to a lesser extent. The approximate value of the total shrinkage strain for design is taken as 0.0003 in the absence of test data (cl. 6.2.4.1).

(vii) Creep of concrete

Figure: Stress-strain curve of concrete

Creep is another time dependent deformation of concrete by which it continues to deform, usually under compressive stress.

Thus, the long term deflection will be added to the short term deflection to get the total deflection of the structure. Accordingly, the long term modulus Ece or the effective modulus of concrete will be needed to include the effect of creep due to permanent loads. The relationship between Ece and Ec is obtained as follows:

     c  f c / Ec

Where, c =short term strain at the age of loading at a stress value of fc

θ=creep co-efficient = cr

c

cr  =ultimate creep strain

It is seen that the value of creep coefficient θ is reducing with the age of concrete at loading. The creep of concrete is influenced by

•         Properties of concrete

•         Water/cement ratio

•         Humidity and temperature of curing

•         Humidity during the period of use

•         Age of concrete at first loading

•         Magnitude of stress and its duration

•         Surface-volume ratio of the member

(f)  Thermal expansion of concrete

The knowledge of thermal expansion of concrete is very important as it is prepared and remains in service at a wide range of temperature in different countries having very hot or cold climates. Moreover, concrete will be having its effect of high temperature during fire. The coefficient of thermal expansion depends on the nature of cement, aggregate, cement content, relative humidity and size of the section. IS 456 stipulates (cl. 6.2.6) the values of

o

Coefficient of thermal expansion for concrete    / C  for different types of aggregate.

Workability and Durability of Concrete

Workability and durability of concrete are important properties to be considered. The relevant issues are discussed in the following:

The workability of a concrete mix gives a measure of the ease with which fresh concrete can be placed and compacted. The concrete should flow readily into the form and go around and cover the reinforcement, the mix should retain its consistency and the aggregates should not segregate. The main factor affecting workability is the water content of the mix. Admixtures will increase workability but may re strength. The size of aggregate, its grading and shape, the ratio of coarse to fine aggregate and the aggregate-to-cement ratio also affect workability to some degree.

Measurement of workability

(a) Slump test

The fresh concrete is tamped into a standard cone which is lifted off after filling and the slump is measured. The slump is 25–50 mm for low workability, 50–100 mm for medium workability and 100–175 mm for high workability. Normal reinforced concrete requires fresh concrete of medium workability. The slump test is the usual workability test specified.

(b) Compacting factor test

The degree of compaction achieved by a standard amount of work is measured. The apparatus consists of two conical hoppers placed over one another and over a cylinder. The compacting factor is the ratio of the weight of concrete in the cylinder to the weight of an equal volume of fully compacted concrete. The compacting factor for concrete of medium workability is about 0.9.

Durability of concrete

A durable concrete performs satisfactorily in the working environment during its anticipated exposure conditions during service.. For more information, please refer to cl. 8 of IS 456.

Design mix and nominal mix concrete

In design mix, the proportions of cement, aggregates (sand and gravel), water and mineral admixtures, if any, are actually designed, while in nominal mix, the proportions are nominally adopted. The design mix concrete is preferred to the nominal mix as the former results in the grade of concrete having the specified workability and characteristic strength (vide cl. 9 of IS 456).

Batching

Mass and volume are the two types of batching for measuring cement, sand, coarse aggregates, admixtures and water. Coarse aggregates may be gravel, grade stone chips or other man made aggregates. The quantities of cement, sand, coarse

Aggregates and solid admixtures shall be measured by mass. Liquid admixtures and water are measured either by volume or by mass (cl. 10 of IS 456).

3.5 Properties of Reinforcing steel

Steel reinforcement used in reinforced concrete may be of the following types

(a) 1. Mild steel bars conforming to IS 432 (part-I) 2. Hot rolled mild steel conforming to IS 1139

(b) 1. Medium tensile steel conforming to IS 432 (part-I) 2. Hot rolled medium tensile steel.

(c) 1. Hot rolled High Yield Strength Deformed (HYSD) steel conforming to IS 1139. 2. Cold-worked steel HYSD bars steel conforming to IS 1786.

(d) 1. Hard drawn steel wire fabric conforming to IS 1566.

2. Rolled steel made from structural steel conforming to Is 226.

1. The most important characteristic of a reinforcing bar is its stress strain curve and the important property yield stress or 0.2% proof stress, as the case may be.

2. The modules of elasticity E for these steel is 2x105 N/mn2.

3. Mild steel bars have yield strength of 250 N/mm2 and hence it is known as Fe 250.

4.  HYSD bars may be hot rolled high yield strength bars or cold rooked steel high strength deformed bars. The latter are also known as cold twisted deformed bars or Tor steel and are available in different grades

i)   Fe 415 ii) 500 iii) Fe 550 having 0.2% proof stress as 415N/mm2, 500N/mm2 and 550 N/mm2

5. The reinforcing bars should have sufficient % of elongation.

6. Its coefficients of thermal expansion should be more or less equal to the cement concrete.

Stress-strain curves for reinforcement

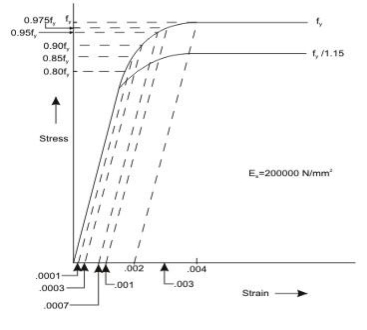
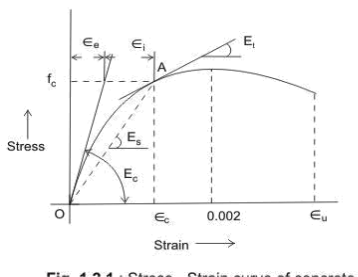
Figure: Stress-strain curve for Mild steel (idealised) (Fe 250) with definite yield point

Figures 1.2 and 1.3 show the representative stress-strain curves for steel having definite yield point and not having definite yield point, respectively.

For cold-worked bars (Fig. 1.3), the stress is proportional to the strain up to a stress of 0.8 fy.

Thereafter, the inelastic curve is defined as given below:

3.6 Wind Load & Earthquake Load

• Wind Loads

The force exerted by the horizontal component of wind is to be considered in the design of buildings. It depends upon the velocity of wind, shape and size of the building. The method of calculating wind load on structure is given in IS 875 (Part-3): 1987.

• Earthquake Loads

Earthquake loads depend upon the place where the building is located. As per 1893-2002 (Part-I) (General Provisions for Buildings), India is divided into four seismic zones. The code gives recommendations for earthquake resistant design of structures. Now, it is mandatory to follow these recommendations for design of structures.

3.7 DESIGN PHILOSOPHIES (Method of RCC design)

A reinforced concrete structure should be designed to satisfy the following criteria-

• Adequate safety, in items stiffness and durability
• Reasonable economy.

The following design methods are used for the design of RCC Structures.

• The working stress method (WSM)
• The ultimate load method (ULM)
• The limit state method (LSM)

Working Stress Method (WSM)

This method is based on linear elastic theory or the classical elastic theory. This method ensured adequate safety by suitably restricting the stress in the materials (i.e. concrete and steel) induced by the expected working leads on the structures.

The WSM uses a factor of safety of about 3 with respect to the cube strength of concrete and a factor of safety of about 1.8 with respect to the yield strength of steel.

Ultimate load method (ULM)

The method is based on the ultimate strength of reinforced concrete at ultimate load is obtained by enhancing the service load by some factor called as load factor for giving a desired margin of safety .Hence the method is also referred to as the load factor method or the ultimate strength method.

In the ULM, stress condition at the state of in pending collapse of the structure is analysed, thus using, the non-linear stress – strain curves of concrete and steel. The safely measure in the design is obtained by the use of proper load factor.

Limit state method (LSM)

Limit states are the acceptable limits for the safety and serviceability requirements of the structure before failure occurs. The design of structures by this method will thus ensure that they will not reach limit states and will not become unfit for the use for which they are intended.

Limit state are two types

i) Limit state of collapse

Ii) Limit state of serviceability.

Limit states of collapse

The limit state of collapse of the structure or part of the structure could be assessed from rupture of one or more critical sections and from bucking due to elastic bending, shear, torsion and axial loads at every section shall not be less than the appropriate value at that section produced by the probable most unfavorable combination of loads on the structure using the appropriate factor of safely.

Limit state of serviceability

Limit state of serviceability deals with deflection and crocking of structures under service loads, durability under working environment during their anticipated exposure conditions during service, stability of structures as a whole, fire resistance etc.

Characteristic and design values and partial safety factor

1. Characteristic strength of materials.

The term characteristic strength means that value of the strength of material below which not more than minimum acceptable percentage of test results are expected to fall. IS 456:2000 have accepted the minimum acceptable percentage as 5% for reinforced concrete structures. This means that there is 5% for probability or chance of the actual strength being less than the characteristic strength.

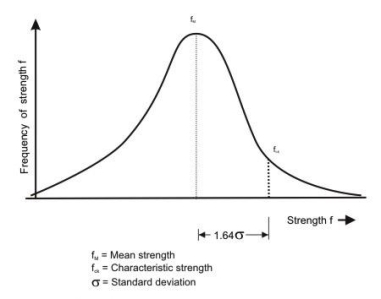
Figure 1.4: Frequency distribution curve for strength

Figure shows frequency distribution curve of strength material (concrete or steel). The value of K corresponding to 5% area of the curve is 1.65.

The design strength should be lower than the mean strength (fm) Characteristic strength = Mean strength –K x standard deviation or

fk=fm-KSd

Where, fk=characteristic strength of the material

fm=mean strength

K=constant =1.65

Sd=standard deviation for a set of test results.

IS 456:2000 has recommended minimum value of n=30.

Characteristic strength of concrete

Characteristic strength of concrete is denoted by fck (N/mm2) and its value is different for different grades of concrete e.g. M 15, M25 etc. In the symbol ‗M‘ used for designation of concrete mix, refers to the mix and the number refers to the specified characteristic compressive strength of 150 mm size cube at 28 days expressed in N/mm2

Characteristic strength of steel

Until the relevant Indian Standard specification for reinforcing steel are modified to include the concept of characteristic strength, the characteristic value shall be assumed as the minimum yield stress or 0.2% proof stress specified in the relevant Indian Standard specification. The characteristic strength of steel designated by symbol fy (N/mm2)

Characteristic loads

The term ‗Characteristic load‘means that values of load which has a 95% probability of not being exceeded during that life of the structure.

Figure 1.5: Frequency distribution curve for load

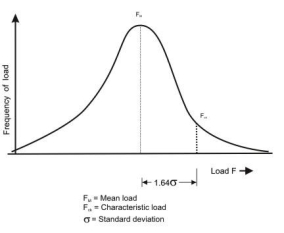
The design load should be more than average load obtained from statistic, we have

Fk=Fm+KSd

Where, Fk=characteristic load;

Fm= mean load

K=constant=2.65;

Sd=standard deviation for the load.

Since data are not available to express loads in statistical terms, for the purpose of this standard, dead loads given in IS 875(Part-1), imposed loads given in IS 875(Part-2), wind loads. Given in IS 875 (Part-3), snow load as given in IS 875(Part-4) and seismic forces given in IS 1893 shall be assumed as the characteristic loads.

Design strength of materials

The design strength of materials (fd) is given by

fd   fk

m

Where, fk= characteristic strength of material.

                  m = partial safety factor appropriate to the material and the limit state being considered

Design loads

The design load ( Fd) is given by.

Fd=Fk.  f

                  f =  partial safety factor appropriate to the nature of loading and the limit state being considered.

The design load obtained by multi plying the characteristic load by the partial safety factor for load is also known as factored load.

Partial safety factor (  m) for materials

When assessing the strength of a structure or structural member for the limit state of collapse, the values of partial safety factor,  m should be taken as 1.15 for steel.

Thus, in the limit state method, the design stress for steel reinforcement is given by fy /  ms = fy/1.15=0.87fy.

According to IS 456:2000 for design purpose the compressive strength of concrete in the structure shall be assumed to be 0.67 times the characteristic strength of concrete in cube and partial safety factor  mc =1.5 shall be applied in addition to this. Thus, the design stress in concrete is given by

0.67 f ck / mc  0.67 f ck / 1.5  0.446 fck

Partial safety factor for loads

The partial safety factors for loads, as per IS 456:2000 are given in table below

(* This value is to be considered when stability against overturning or stress reversal is critical)

Limit state of collapse in flexure

The behavior of reinforced concrete beam sections at ultimate loads has been explained in detail in previous section. The basic assumptions involved in the analysis at the ultimate limit state of flexure (Cl. 38.1 of the Code) are listed here.

a)  Plane sections normal to the beam axis remain plane after bending, i.e., in an initially straight beam, strain varies linearly over the depth of the section.

b) The maximum compressive strain in concrete (at the outermost fibre) cu  shall be taken as

0.0035 in bending.

c)  The relationship between the compressive stress distribution in concrete and the strain in concrete may be assumed to be rectangle, trapezoid, parabola or any other shape which results in prediction of strength in substantial agreement with the results of test. An acceptable stress-strain curve is given below in figure 1.6. For design purposes, the compressive strength of concrete in the structure shall be assumed to be 0.67 times the characteristic strength. The partial safety factor y, = 1.5 shall be applied in addition to this.

Figure 1.6 Stress-strain curve for concrete

d) The tensile strength of the concrete is ignored.

e) The stresses in the reinforcement are derived from representative stress-strain curve for the

Type of steel used. Typical curves are given in figure 1.3. For design purposes the partial safety factor  m equal to 1.15 shall be applied.

f)  The maximum strain in the tension reinforcement in the section at failure shall not be less

Limiting Depth of Neutral Axis

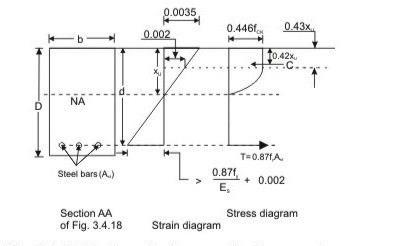
Figure: 1.7 Rectangular beam under flexure xu  xu,max

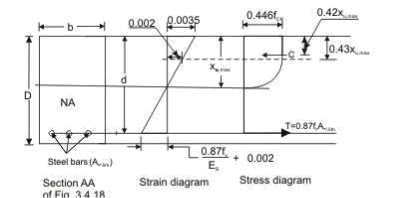
Figure 1.8 Rectangular beam under flexure xu  xu,max

The values of xu,max for different grades of steel, obtained by applying Eq. (2), are listed in table.

Table 1 Limiting depth of neutral axis for different grades of steel

The limiting depth of neutral axis  xu,max corresponds to the so-called balanced section, i.e., a

Section that is expected to result in a ‗balanced‘ failure at the ultimate limit state in flexure. If the neutral axis depth xu is less than xu,max , then the section is under-reinforced (resulting in

a ‗tension‘ failure); whereas if xu exceeds xu,max , it is over-reinforced (resulting in a ‗compression‘ failure).

3.8 Assumptions For Limit State method :

• Plane sections normal to the axis remain plane after bending.
• The maximum strain in concrete at the outermost compression fibre is taken as 0.003 5 in bending.
• The relationship between the compressive stress distribution in concrete and the strain in concrete may be assumed to be rectangle, trapezoid, parabola
• The tensile strength of the concrete is ignored.
• The stresses in the reinforcement are derived from representative stress-strain curve for the type of steel used.. For design purposes the partial safety factor Y m ' equal to 1.15 shall be applied.

3.9 Code of Practices

Reference Books:

1. RCC Design and drawing By Neelam Sharma
2. Limit state design of reinforced concrete by P.C. Verghese, PHI
3. Reinforced concrete: Limit state by A.K. Jain
4. Reinforced concrete by B.C. Punamia, A.K. Jain and A.K. Jain
5. IS Code 456:2000