Unit-4
Non-Uniform Flow
- Non-uniform flow results from gradual or sudden changes in the cross- sectional area. Uniform flow and varied flow describe the changes in depth and velocity with respect to distance. Varied flow or non-uniform flow occurs when depth or velocity change over a distance, like in a constriction or over a riffle.
- Flow is said to be non-uniform, when there is a change in velocity of the flow at different points in a flowing fluid, for a given time. For example, the flow of liquids under pressure through long pipelines of varying diameter is referred to as non-uniform flow.
1. For a non-uniform flow, the changes with position may be found either in the direction of flow or in directions perpendicular to it.
2. Non-uniformity in a direction perpendicular to the flow is always encountered near solid boundaries past which the fluid flows.
Reason: All fluids possess viscosity which reduces the relative velocity (of the fluid with respect to the wall) to zero at a solid boundary. This is known as no-slip condition.
- If the water surface is parallel to the channel bottom flow is uniform and the water surface is at normal depth.

- Non-Uniform flow occurs due to:
- Change in direction: If the direction of velocity is changes, the flow becomes non-uniform flow.
- Change in depth: It occurs due to change in the cross-section of the channel, change in discharge, Change in bed slope of the channel, Presence of a control section.
- Gradually varied flow and rapidly varied flow are two types of non-uniform flow.
- In open channel flow, specific energy (E) is the energy length, or head, relative to the channel bottom. Specific energy is expressed in terms of kinetic energy, and potential energy, and internal energy. The three energy components in Bernoulli's equation are elevation, pressure and velocity.
- Specific energy is energy per unit mass. It is also sometimes called gravimetric energy density or just energy density though energy density more precisely means energy per unit volume.
- Specific energy in a channel section defined as the energy per unit weight of liquid at any section of a channel measured with respect to bottom of channel.
Specific energy
E = y 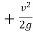
Where y = depth of liquid flow
V = velocity of water = 
- The area of flow A is dependent upon the channel geometry and the depth of flow but for given channel section it will be dependent upon depth of flow. The variation of specific energy can be studied into two ways:
- For the constant discharge Q, the variation of specific energy E with depth of flow y can be obtained.
- For the constant specific energy E, the variation of discharge Q with depth of flow y can be obtained.
E = y + 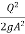 = f(y,Q)
= f(y,Q)
For a given cross-section of channel and known discharge Q, the specific energy is the function of depth of flow ‘y’ alone.
E = f(y)
The curve plotted between energy on x-axis and depth of flow on y-axis for a given section A and given discharge Q, the curve obtained is called as specific energy curve.
The specific energy curve, the straight line QA represents static energy with respective x-axis at an angle 45 .
.
The curve FG represents kinetic energy head 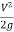 for various value of depth ‘y’, which is parabolic curve.
for various value of depth ‘y’, which is parabolic curve.
The curve BCD represents specific energy head which is obtained by adding value of static energy head (QA) and kinetic energy head (MN).
The depth ‘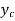 ’ corresponding to the point C at which specific energy head as minimum is called as the critical depth.
’ corresponding to the point C at which specific energy head as minimum is called as the critical depth.
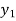 and
and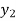 represents the depth of flow below and above the critical depth respectively.
represents the depth of flow below and above the critical depth respectively.
When the depth of flow is less than the critical depth of flow, the flow is called super critical flow or rapid flow or shooting flow.
When the depth of flow is greater than the critical depth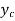 , the flow is called as subcritical flow or streaming flow or tranquil flow.
, the flow is called as subcritical flow or streaming flow or tranquil flow.
The two depth y1 and y2 to the right of point C where specific energy E1 and E2 remain same, this depth is called as alternate depth.
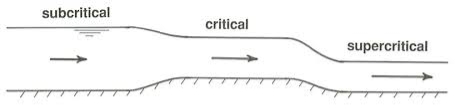
- Critical flow occurs when the flow velocity in a channel equals the wave velocity generated by a disturbance or obstruction. In this condition the Froude number (Fr) = 1. When the wave velocity exceeds the flow velocity (Fr is less than 1) waves can flow upstream, water can pond behind an obstruction, and the flow is said to be subcritical or tranquil.
- When Fr is greater than 1 wave cannot be generated upstream and the flow is said to be supercritical, rapid, or shooting. In this condition a standing wave is T formed over obstructions in the river bed. In nature, supercritical flow is found only in rapids and waterfalls, but it is often created artificially by weirs and flumes with the aim of measuring discharge.
- The specific energy of a liquid flowing in an open channel is defined to be the sum of its kinetic and potential energy per unit weight of flowing liquid, relative to the channel bottom. This is the point that is defined to have critical flow conditions (occurring a depth of flow = critical depth).
- The flow at which the specific energy is the minimum for a given discharge is called as critical flow.
E = y + 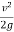 = y +
= y + 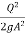
For minimum specific energy, 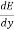 = 0
= 0
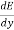 = 1 +
= 1 + 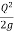 (-
(-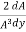 )
)
Let T be the top width of channel,
Area of channel dA = T dy, dA/dy = T
Substituting value of dA/dy , we get
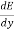 = 1 +
= 1 + 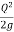 (-
(-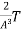 ) = 1-
) = 1- 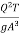 = 0
= 0
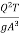 = 1
= 1
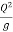 =
= 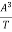
Hence, this equation represents the critical flow condition
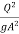 =
= 
Let D is the hydraulic depth = 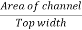 =
= 
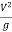 = D
= D
 =
= 
Velocity head =  hydraulic depth
hydraulic depth
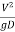 = 1
= 1
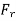 =
= 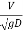 = 1
= 1
For critical flow, Froude number is unity.
- Critical depth can also be defined as the depth producing maximum discharge for given specific energy.
- Specific energy curve will be change, if the discharge in the channel changes and correspondingly, the depth-discharge curve.
From fig. The point C1, C2, C3, .......Cn are points on the specific energy curve corresponding to critical flow.
If 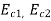 are minimum specific head corresponding to the critical depth
are minimum specific head corresponding to the critical depth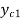 ,
, 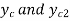 then,
then,
Tan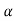 =
= 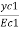 =
= 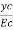 =
= 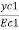
We know 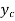 =
= 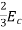
Tan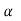 =
= 
- The specific force is the function of the depth of flow, channel geometry and discharge.
- For a given channel section and a given discharge the specific force is a function of the depth of flow only.
- The graphical representation of specific force F against the depth of flow for a given discharge Q in a channel results in a parabolic curve, this curve is known as specific force curve
- For the given value of specific force, it is observed that there are two possible depth y1 and y2.
- The depth y1 lies in super critical region and is known as initial depth.
The depth y2 lies in the sub-critical region flow is known as the sequent depth.
These depth y1 and y2 are known as conjugate depth.
The point C corresponds to the minimum specific force where two depths merge into one to yield a single depth 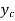 is known as critical depth.
is known as critical depth.
Average water depth in a stream channel or conduit computed by dividing the cross-sectional area by the surface width.
The depth of flow at which the specific energy is minimum is called as critical depth.
Velocity of flow is also minimum.
At critical depth Froude number is one.
An open channel transition is the portion of a channel with varying cross-section which connects one uniform channel to other, which may or may not have same shape.
Transition may cause due to:
a) Reduction in width of channel
b) Increase in width of channel
c) Gradual rise in bottom of channel
d) Gradual depression in bottom of channel
e) Gradual contraction followed by gradual expansion or vice versa.
f) Bridge pier construction across channel cross section.
The concept of specific energy and discharge diagram may be used for analysis of transition in a rectangular open channel.
It is assumed for analysis of transition that there is no loss of energy in the transition.
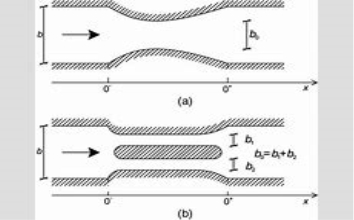
- Venturi Flume:
Venturi flume is device in which the velocity of flow at at that throat is less than the critical velocity, so that no standing wave will occur in the flume.
It is the artificial hydraulic structure constructed in an open channel.
Consider A, B, H, V and a, b, b, v are the area of section width, depth of flow and velocities at entrance of flume and at the throat respectively.
At the throat, the velocity is increase due to reduction in channel cross-section, which will lead to drop in water level at the throat.
By Continuity equation,
Q = AV = av
V =  v
v
By Bernoulli’s equation,
H + 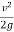 = h +
= h + 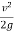
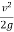 -
- 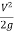 = H - h
= H - h
 -
- 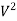 = 2g(H - h)
= 2g(H - h)
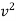 –
– 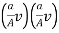 = 2g (H – h)
= 2g (H – h)
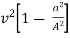 = 2g (H – h)
= 2g (H – h)
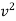 -
- 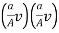 = 2g (H – h)
= 2g (H – h)
v = 
Theoretical Discharge 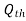 = av = aA
= av = aA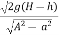
Where 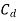 = Coefficient of discharge
= Coefficient of discharge
Modular Flume or Standing Flume:
- Modular Flume or standing flume is a device in which the velocity of flow at the throat is greater than the critical velocity, resulting in the formation of standing wave in the flume.
- In this type of venture-flume, the value of b and h are decrease upto critical depth. Therefore, velocity of throat will be equal to critical velocity.
- Downstream of throat section is followed by flared transition section design to restore the stream to its original width.
- Since the velocity of throat is greater than the critical velocity, the depth of flow at a section upstream remains unaffected by variations in the downstream depth until the downstream depth become greater than about 0.7 of the upstream depth.
- The discharge through a standing wave flume is the function of only depth of flow H and it is expressed by the relationship.
Q = 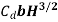
Where, b = width of throat
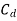 = coefficient of discharge of flume = 1.706
= coefficient of discharge of flume = 1.706
Parshall Flume:
- The Parshall flume is an open channel flow metering device that was developed to measure the flow of surface waters and irrigation flows. The Parshall flume is a fixed hydraulic structure. It is used to measure volumetric flow rate in industrial discharges, municipal sewer lines, and influent/effluent flows in wastewater treatment plants.
- The Parshall flume accelerates flow through a contraction of both the parallel sidewalls and a drop in the floor at the flume throat. Under free-flow conditions the depth of water at specified location upstream of the flume throat can be converted to a rate of flow. Some states specify the use of Parshall flumes, by law, for certain situations (commonly water rights).
- The design of the Parshall flume is standardized under ASTM D1941, ISO 9826:1992, and JIS B7553-1993. The flumes are not patented and the discharge tables are not copyright protected.
- A total of 22 standard sizes of Parshall flumes have been developed, covering flow ranges from 0.005–3,280 cfs (0.1416–92,890 l/s).
- Submergence transitions for Parshall flumes range from 50% (1–3 in sizes) to 80% (10–50 ft sizes),beyond which point level measurements must be taken at both the primary and secondary points of measurement and a submergence correction must be applied to the flow equations. It is important to note that the secondary point of measurement (Hb) for a Parshall flume is located in the throat, measuring Hb can be difficult as flow in the throat of the flume is turbulent and prone to fluctuations in the water level. 90% is viewed as the upper limit for which corrections for submerged flow are practical.
- Under laboratory conditions Parshall flumes can be expected to exhibit accuracies to within ±2%, although field conditions make accuracies better than 5% doubtful. A modified version of the Venturi flume is the Parshall flume. Named after it creator, Dr. Ralph L. Parshall of the U.S. Soil Conservation Service, the Parshall flume is a fixed hydraulic structure used in measuring volumetric flow rate in surface water, wastewater treatment plant, and industrial discharge applications. The Parshall flume accelerates flow through a contraction of both the parallel sidewalls and a drop in the floor at the flume throat. Under free-flow conditions the depth of water at specified location upstream of the flume throat can be converted to a rate of flow.

The free-flow discharge can be summarized as
Q = C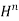
Where,
- Q is flow rate
- C is the free-flow coefficient for the flume
- H is the head at the primary point of measurement
- n varies with flume size
- When the downstream depth is high enough that the transition to subcritical flow advances upstream into the throat and the hydraulic jump disappears, the flume is operating in a "submerged flow" regime, and the discharge is instead given by
Q = C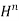 –
– 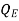
- Where,
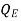 is the submergence correction, and is found using pre-determined tables for a particular flume geometry.
is the submergence correction, and is found using pre-determined tables for a particular flume geometry.
- The Parshall flume is an empirically calibrated device, so interpolation between listed sizes is not an accurate way to make intermediate size flumes. The flumes are not scale models of each other. 22 standard sizes of Parshall flumes have been developed, covering flow ranges from 0.005 cfs [0.1416 l/s] to 3,280 cfs [92,890 l/s].
- Submergence transitions for Parshall flumes range from 50% (1–3 in sizes) to 80% (10–50 ft sizes),[6] beyond which point level measurements must be taken at both the primary and secondary points of measurement and a submergence correction must be applied to the flow equations.
- Under laboratory conditions Parshall flumes can be expected to exhibit accuracies to within ±2%, although field conditions make accuracies better than 5% doubtful.
- Not all Parshall flumes have the energy-recovering divergence section. These flumes, called Montana flumes, or short section parshall flumes, must instead have a free-spilling discharge at all expected flow rates, which increases the drop along the whole flume system. The measurement calculations are the same as for free-flow in a standard Parshall flume, but submerged flow cannot be adjusted for.
- Differences between the Venturi and Parshall flume include: reduction of the inlet converging angle, lengthening the throat section, reduction of the discharge divergence angle, and introducing a drop through the throat (and subsequent partial recovery in the discharge section).
Broad Crested Weir:
Broad crested weirs are robust structures that are generally constructed from reinforced concrete and which usually span the full width of the channel. They are used to measure the discharge of rivers, and are much more suited for this purpose than the relatively flimsy sharp crested weirs.
- Function:
Commonly, weirs are used to prevent flooding, measure water discharge, and help render rivers more navigable by boat. In some locations, the terms dam and weir are synonymous, but normally there is a clear distinction made between the structures. Usually, a dam is designed specifically to impound water behind a wall, whilst a weir is designed to alter the river flow characteristics.
A common distinction between dams and weirs is that water flows over the top (crest) of a weir or underneath it for at least some of its length. Accordingly, the crest of an overflow spillway on a large dam may therefore be referred to as a weir. Weirs can vary in size both horizontally and vertically, with the smallest being only a few inches in height whilst the largest may be many metres tall and hundreds of metres long. Some common weir purposes are outlined below.
- Flow measurement:
Weirs are allows hydrologists and engineers a simple method of measuring the volumetric flow rate in small to medium-sized streams/rivers or in industrial discharge locations. Since the geometry of the top of the weir is known and all water flows over the weir, the depth of water behind the weir can be converted to a rate of flow. However, this can only be achieved in locations where all water flows over the top of the weir crest (as opposed to around the sides or through conduits or sluices) and at locations where the water that flows over the crest is carried away from the structure. If these conditions are not met, it can make flow measurement complicated, inaccurate, or even impossible.
The discharge calculation can be summarised as:
Q = 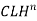
Where:
- Q is the volumetric flow rate of fluid (the discharge)
- C is the flow coefficient for the structure (on average a figure of 0.62).
- L is the width of the crest
- H is the height of head of water over the crest
- n varies with structure (e.g., 3/2 for horizontal weir, 5/2 for v-notch weir)However, this calculation is a generic relationship and specific calculations are available for the many different types of weir. Flow measurement weirs must be well maintained if they are to remain accurate.
- Current Meter:
The current velocity meter allows you to measure stream flow velocity in feet or meters per second and measure water depth in hundredths of a foot up to three feet. The average stream flow velocity times the cross-sectional area of the stream determines the stream flow measurement in cubic feet or meters per second.
The current meter is used to measure water velocity at predetermined points (subsections) along a marked line, suspended cableway, or bridge across a river or stream. The depth of the water is also measured at each point.
The velocity of flow at any point in the open channel can be most accurately and conveniently determined by means of a mechanical device named current-meter. Current-meter of common use may be classified in two categories according to the type of revolving part used.
Figures 15.6 and 15.7 give clear idea about two types of current-meters. In Fig. 15.6 Price current-meter is shown in which a wheel of conical cups (6 to 8) is mounted on arms of a vertical axis. In Fig. 15.7 Amsler current-meter is shown in which a series of helicoidal vanes is mounted on a horizontal axis.
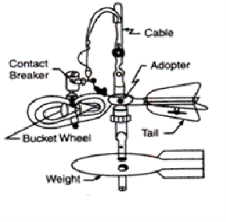
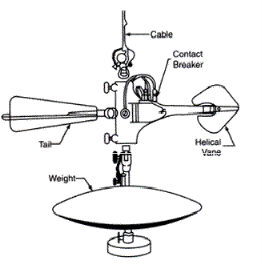
The first type of current-meter is better in the following respects:
i. Frictional resistance is usually less.
Ii. It starts working even in a current of small velocity.
Iii. It does not revolve too rapidly under high velocity flow.
Iv. It tends to measure full velocity of flow even if it is not oriented very accurately.
v. In turbulent flow it over-registers the velocity. On the other hand propeller type current meter under registers velocities by about same amount.
Only disadvantages of conical type current-meter are that while lowering the cup wheel starts rotating even if the water is still.
The current-meter with conical cups is more popular because of its accuracy and efficient working.
In principle the working of the two types is based on the same theory and can be outlined as mentioned below:
- Working of Current-Meters:
When the meter is lowered in water and when it faces the current of water in the channel the wheel rotates. To keep the meter facing the direction of flow a tail is attached. This tail aligns the meter in the direction of flow. The meter is also fitted with a streamlined weight (fish weight) which keeps the meter in a vertical position. The rate of rotation of the wheel depends on the velocity of flow. A dry battery is kept on the shore or in a boat and an electric current is passed to the wheel from it. A commutator is fixed to the shaft of the revolving wheel.
It makes and breaks the contact in an electrical circuit at each revolution. An automatic revolution counter is kept in the boat or on the shore with the battery which registers the revolutions. When an electric circuit is broken an electric bell in the boat rings or a head phone m the boat buzzes. Then the time taken for a required number of revolutions may be noted. The velocity of flow can be read from a rating table. The rating table is always provided with the meter.
2. Rating of Current-Meter:
The speed of rotation of the cup wheel is a function of the velocity of flow. The cup wheel rotates due to relative velocity between water and the cup wheel. This fact is utilized in calibration of the current-meter. Current-meter is rated in a long tank (say 150 m long) with sectional area 4 m x 2.5 m. On both sides of the tank rails are provided.
A trolley runs over the rails with known velocities. Generally equipment is provided on the trolley to automatically record the current-meter revolutions, time and distance travelled.
A current-meter is lowered in the still water of the tank from the trolley by a suspension rod. The trolley is run over the tank at different known velocities for number of times. The number of rotations of the current-meter cup wheel for various velocities are noted.
From the readings a rating curve is prepared. It comes out to be a straight line and the equation is of the form V = M R + C where V is velocity, R is revolutions of cup wheel per second and M and C are constants. Every current-meter whether new or old should be rated before putting it into use. In addition it is essential to calibrate every current-meter periodically.
3. Methods of Supporting Current-Meters:
So far as possible the current-meter should be suspended in the similar way as it done for ratings. When the depth of water in the channel is more, the current-meter is suspended by means of a fine cable or a wire rope and lowered to the required depth. Here it becomes necessary to use a boat for suspending the current-meter. The boat should be pig. 15.8. Current-meter measurement in equipped with the arrangement required for raising rivers and lowering the meter (Fig. 15.8).
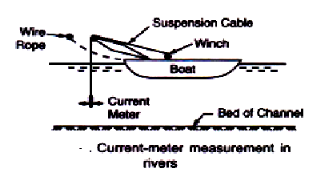
The boat is moored to the wire rope which is stretched across the river, at the determined point in the river. When the channel carries water at shallow depths the suspension cable and the weight is removed and the current-meter is mounted on a wading rod. The rod is made to rest on the channel bed at required position for taking measurements. In this method as the water is shallow boat is not required. The current-meter may be fixed at any depth on the wading rod for observing velocity.
4. Methods of Measuring Velocity:
When the velocity is measured by the current-meter at 0.5 D then to get mean velocity of the section the observed velocity should be multiplied with a coefficient 0.96. Alternatively, to obtain mean velocity of flow at a particular section, velocities may be observed at 0.2 and 0.8 of depth from water surface.
The mean of these two readings gives mean velocity of flow at that section. Generally mean velocity of flow at a section is obtained by keeping the meter at 0.6 B. In the observed velocity corrections are made for any obliquity of the current with the cross-section line and also for drift. It is necessary to conduct vertical velocity distribution experiment at each site to decide point of average velocity.
B. Floats:
A subsurface float consists of a submerged float attached to a surface float by an adjustable line and it measures directly the mean velocity. The float method is used especially in the measurement of flood discharge where excessive velocities, depths and floating debris prohibit the use of other methods.
This method measures surface velocity. Mean velocity is obtained using a correction factor. The basic idea is to measure the time that it takes the object to float a specified distance downstream. Velocity V = travel distance/ travel time because surface velocities are typically higher than mean or average velocity.
V mean = k V surface where k is a coefficient that generally ranges from 0.66 to 0.75, depending on channel depth.
Choose a suitable straight reach with minimum turbulence (ideally at least 3 channel widths long).
- Mark the start and end point of your reach.
- If possible, travel time should exceed 20 seconds.
- Drop your object into the stream upstream of your upstream marker. Start the watch when the object crosses the upstream marker and stop the watch when it crosses the downstream marker.
- You should repeat the measurement at least 3 times and use the average in further calculations.
Ex. Travel Distance = 50 feet1strun = 34 sec.2ndrun = 32 sec.3rdrun = 28 sec. k = 0.7average run = 31.3 sec. Velocity = (50 feet / 31.3sec.) * 0.7= 1.1feet/sec
Area= average width * average depth. Measure stream’s width and depth across at least one cross section where it is safe to wade. If possible, measure depth across the stream's width at the start and stop cross sections and average the two but if only measuring one cross section choose the one downstream. Use a marked rod, a yard or meter stick to measure the depth at regular intervals across the stream. Five depth measurements are typical but more is better, especially in larger streams. Average your cross-sectional areas (A): Using the average area and corrected velocity, you can now compute discharge Q.

C. Hot-Wire Anemometer:
A hot-wire anemometer is a thermal transducer which has been widely used to measure instantaneous flow velocity. The use of the hot-wire anemometer permits instantaneous flow velocity to be calculated from electric voltage measurements.
The advantage of hot-wire anemometry is associated with its very high spatial resolution and excellent frequency response characteristics. In most cases, the probe-stem is perpendicularly aligned with the mainstream direction of flow. The direction of mainstream flow coincides with the x-axis and the axis of the hot-wire probe is initially aligned with the y-axis. The most essential part of the hot-wire anemometer is the thin wire sensor where forced convective heat transfer takes place from the wire to flow over the wire.

- Dynamic equation of gradually varied flow:
Consider B width of wide regular channel and y is the depth of flow
Mean hydraulic radius 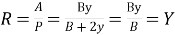
By manning’s formula
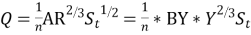 ------1
------1

Manning’s constant n is assumed same for uniform and non uniform flow
Dividing equation 1 to 2 we get
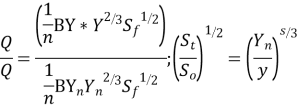
We know that 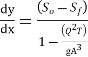
For wide channel
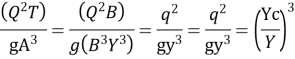
Substituting equation 4 , we get
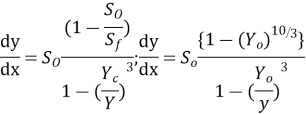
This is dynamic equation of GVF in a wide channel .
Ii. Classifications Of Surface Profile:
Mild slope:
Mild Slope is less than the critical slope and the normal depth is greater than critical depth (yn>yc). The flow is subcritical and controlled downstream. M1 profiles are common where mild slope streams enter a pool. M2 profiles can occur upstream of a sudden enlargement in a channel or where the slope becomes steeper.
Mild Slope is less than the critical slope and the normal depth is greater than critical depth (yn>yc). The flow is subcritical and controlled downstream.M1 profiles are common where mild slope streams enter a pool.M2 profiles can occur upstream of a sudden enlargement in a channel or where the slope becomes steeper.
Horizontal Slope:
The normal depth  is not defined in a horizontal bed channel, it may be less than
is not defined in a horizontal bed channel, it may be less than 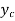 or greater than
or greater than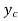 , and such slope of water surface is called as horizontal slope profile.
, and such slope of water surface is called as horizontal slope profile.
Critical Slope:
Critical slope is a key parameter occurring in the analysis of varied flow in open channels. The analysis of varied flow under various operating conditions is required for design of canals.
When 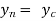 then the flow is known as critical flow and slope is called as critical slope.
then the flow is known as critical flow and slope is called as critical slope.
Steep Slope:
When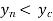 , then the flow is known as rapid flow and slop of free water surface is known as steep slope profile.
, then the flow is known as rapid flow and slop of free water surface is known as steep slope profile.
CHUTE is a channel having steep slopes. These Kinds of Open Channel DROP is similar to a chute, but the change in elevation is affected in a short distance.
Adverse Slope:
When the slope of the channel is increase in the direction of flow. The slope of water at bottom is called as adverse slope.
When 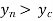 , then the slope is adverse slope.
, then the slope is adverse slope.
Iii. Characteristics Of Surface Profile:
a) Normal depth (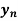 ): Normal depth is the depth of flow in a channel or culvert when the slope of the water surface and channel bottom is the same and the water depth remains constant. Normal depth occurs when gravitational force of the water is equal to the friction drag along the culvert and there is no acceleration of flow. It is depth of water in the channel when discharge Q is under uniform flow.
): Normal depth is the depth of flow in a channel or culvert when the slope of the water surface and channel bottom is the same and the water depth remains constant. Normal depth occurs when gravitational force of the water is equal to the friction drag along the culvert and there is no acceleration of flow. It is depth of water in the channel when discharge Q is under uniform flow.
b) Critical depth (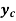 ): Critical depth is defined as the depth of flow where energy is at a minimum for a particular discharge. Critical depth is a quantity of fundamental importance to understanding the flow characteristics. If the actual depth is greater than critical depth, then the flow is considered "subcritical". Subcritical flow is "slow flow" and is impacted by downstream conditions.
): Critical depth is defined as the depth of flow where energy is at a minimum for a particular discharge. Critical depth is a quantity of fundamental importance to understanding the flow characteristics. If the actual depth is greater than critical depth, then the flow is considered "subcritical". Subcritical flow is "slow flow" and is impacted by downstream conditions.
c) Actual depth (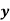 ): The actual depth of flow is the depth of channel measured normal to the direction of flow. Normal depth is the particular depth for which the channel has uniform flow for a given slope and discharge. It is the depth of water in the channel when discharge Q.
): The actual depth of flow is the depth of channel measured normal to the direction of flow. Normal depth is the particular depth for which the channel has uniform flow for a given slope and discharge. It is the depth of water in the channel when discharge Q.
Graphical Approach
Graphical method of computation of water surface is very useful method.
It is used for both prismatic as non-prismatic channel.
Using differential equation of GVF,
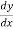 =
= 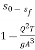
For a given discharge Q, channel shape parameter A, T and  are the function of depth of flow y.
are the function of depth of flow y.
We can write dx = f(y) dy
Consider depth of flow 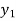 and
and  at a distance
at a distance  and
and 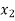 from the control section, then
from the control section, then
(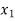 -
- 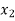 ) =
) = 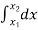 =
= 
Several value of d is assumed and corresponding value of f(y) is calculated.
A curve of h versus f(y) is the plotted.
The area under this curve between y =  and y =
and y = 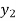 is then calculated.
is then calculated.
The longitudinal distance between two points 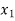 and
and 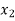 is then determined.
is then determined.
If 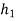 and
and  are very close to each other, then
are very close to each other, then
(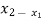 ) =
) = 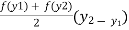
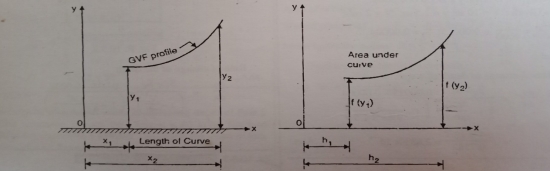
Computation of Water Surface Profile by Numerical Approach.
In this method the length of channel is divided into number of short reaches and the computations are carried out step by step from one end of the reach to the other.
Consider a short reach of channel of length dx between section 1-1 and 2-2 as shown in fig.
Applying Bernoulli’s Equation,
 +
+ 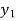 +
+ 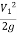 =
= 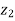 +
+  +
+ 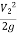 +
+ 
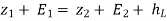
(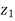 -
- 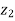 ) = (
) = (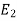 -
- 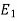 ) +
) + 
Slope of bed 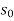 =
= 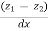
( -
- 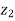 ) = dx
) = dx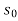
Slope of energy line  =
= 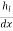
Dx(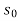 -
-  ) =
) = 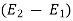
Dx = 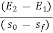
This equation is used for step method of integration. Using the equation of above are computed and total length of curve x = 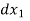 +
+ 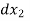 +
+ 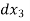 + ....... Is obtained.
+ ....... Is obtained.
The computations are carried out in the upstream direction in case of subcritical flow and downstream direction if the flow is supercritical.
This method is very simple, by choosing proper number of steps, the accuracy of the method can be controlled to the desired degree.
Procedure for direct step method:
- Calculate area of section A, velocity of head, to find specific energy
- Calculate average velocity, velocity of head, to find specific energy.
- Slope of energy line by Chezys formula or Mannings formula.
- Assume new depth at another section, This section should be close to the first section and the increment in d should be small. Compute all the quantities for this new depth as in step1,step2, step3.
- Compute change in energy from E1 to E2.
- The value of energy gradient in equation which is taken as average of energy slope at the two sections 1-1 and 2-2.
- Compute difference between bed slope and average energy slope.
- Compute length of the curve between two section dx.
- Repeat the computation from reach to reach, till the required depth at the other end is reached.
Computation of Water Surface Profile by Analytical Approach.
Analytical method for computation of water surface profile is applicable for a very wide rectangular channel.
A very common method of open-channel flow involves the use of a hydraulic structure such as a weir or flume. Measuring flow into a reservoir is a common application where open-channel flow measurement comes into play. Open-channel flow occurs when liquid flows in a conduit or channel with a free surface.
The energy equation is the base for all methods ofsteady, gradually varied flow computations in open channels. Assuming abscissa x directed opposite the flow.
Z + 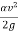 - z + dz +
- z + dz + 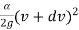 – sdx
– sdx
Where, z– water surface elevation , α– coefficient , v– mean velocity in a cross-section , g–gravity , S– energy line slope (hydraulic slope), original integral one:
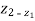 +
+ 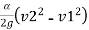 –
–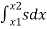
Where, z1 and z2are elevations and v1 and v2are mean velocities incross-sections positioned at x1and x2 respectively.
Considering the rectangular bed cross-section, Eq. (1) can be written as follows:
 -
-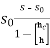
Where, h is depth, hc – critical depth, S0– bed slope. Solution of Eq. (3) requires specification for the energy loss function. Assuming the concept of the infinitely wide channel with a constant bed slope as a base for further considerations, at constant value of Chezy coefficient where the normal depth [m], while Manning’s approach leads to the equation:
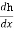 = -
= -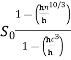
The analytical solution of Eq. (4) is known as the Bresse formula which is for the given initial condition (x0, h0) and at the following denotations:
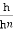 = y,
= y, 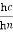 =
= 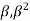 =
= 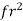
Where, Fris a Froude number for uniform flow.
In this method, the length of channel is divided into number of short reaches and the computations are carried out step by step from one end of reach to the other.
Consider a short reach of channel of length dx.
Applying Bernoullis Equation:
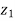 +
+ 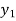 +
+ 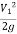 =
=  +
+ 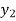 +
+ 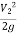 +
+ 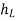

(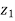 -
- 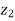 ) = (
) = ( -
- 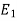 ) +
) + 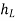
Slope of bed 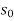 =
= 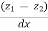
(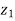 -
- 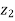 ) = dx
) = dx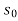
Slope of energy line 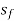 =
= 
Dx(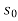 -
- 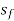 ) =
) = 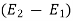
Dx = 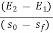
This equation is used for step method of integration. Using the equation of above are computed and total length of curve x = 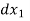 +
+ 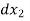 +
+ 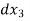 + ....... Is obtained.
+ ....... Is obtained.
The computations are carried out in the upstream direction in case of subcritical flow and downstream direction if the flow is supercritical.
Graphical method of computation of water surface is very useful method.
It is used for both prismatic as non-prismatic channel.
Using differential equation of GVF,
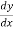 =
= 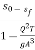
For a given discharge Q, channel shape parameter A, T and 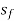 are the function of depth of flow y.
are the function of depth of flow y.
We can write dx = f(y) dy
Consider depth of flow 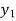 and
and 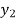 at a distance
at a distance 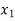 and
and  from the control section, then
from the control section, then
(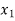 -
- 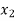 ) =
) = 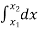 =
= 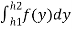
Several value of d is assumed and corresponding value of f(y) is calculated.
A curve of h versus f(y) is the plotted.
The area under this curve between y = 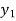 and y =
and y = 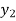 is then calculated.
is then calculated.
The longitudinal distance between two points 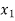 and
and 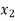 is then determined.
is then determined.
If 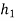 and
and 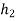 are very close to each other, then
are very close to each other, then
(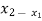 ) =
) = 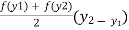
The downstream depth can be calculated using a known upstream depth as follows:
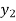 =
= 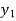 + F(x, y)(
+ F(x, y)(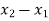 )
)
Similarly, the upstream depth can be calculated using a known downstream depth as follows:
 =
=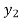 - F(x, y)(
- F(x, y)(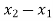 )
)
Where,

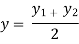
F(x,y) = 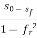
Bresses method is a direct integration method applicable for a very wide rectangular channel.
Chezys formula is used for determination of effect of frictional resistance to the flow.