Unit – 7
Code Excited Linear Prediction
Long-term and short-term linear prediction models are used by the CELP coder. The speech production model's block diagram shows how an excitation sequence is extracted from the codebook through an index. To produce synthetic expression, the extracted excitation is scaled to the required level and filtered by a cascade link of pitch synthesis filter and formant synthesis filter. The formant synthesis filter produces the spectral envelope, while the pitch synthesis filter induces periodicity in the signal associated with the fundamental pitch frequency.
What kind of signal does the excitation codebook contain? The codebook can be set or adaptive, and deterministic pulses or random noise can be used. For the sake of convenience, we'll say the codebook is set and includes white noise samples. As a result, the excitation index selects a white noise sequence from the codebook as input to the synthesis filters' cascade relation. The CELP coder's speech development model is as simple as a white noise source stimulating the synthesis filters. What are the benefits of using this model? As compared to other coders, the following can be noted.
● As with the LPC coder, a strict voiced/unvoiced division is no longer used.
One of the key drawbacks of the LPC coder is rigid classification of a speech frame, which is responsible for significant artifacts in synthetic speech. The cascaded use of the two synthesis filters allows for effective and accurate modeling of transition frames with smoothness and consistency, resulting in synthetic speech that sounds much more natural.
● Partial phase information of the original signal is preserved.
The phase information of the original signal is not retained by the LPC model. The CELP model uses a closed-loop analysis-by-synthesis method to capture some step information. The best excitation sequence from the codebook is chosen in this method, where ‘‘best" means the sequence is capable of producing synthetic speech that is as similar to the original as possible, and ‘‘closeness" is also calculated using time-domain techniques such as signal-to-noise ratio.
The synthetic speech is thus matched not only in the magnitude spectrum domain, but also in the time domain, where a phase difference is significant. Even though a human listener is relatively unaffected by phase, keeping some phase information in the synthetic speech adds naturalness and improves accuracy.
The CELP coder operates well in the mid-bit-rate range and accomplishes this by encoding the excitation sequence using a codebook, which is similar to a vector quantization method in that the entire sequence is encoded with a single index. CELP refers to hybrid-type coders that use an underlying model while attempting to approximate the original waveform at the same time.
Key takeaway:
The speech signal is expressed in a speech coder by a set of parameters such as gain, filter coefficients, voicing powers, and so on. The parameters are extracted from the input signal, quantized, and then used for synthesis in an open-loop method.
Using the parameters to synthesize the signal during encoding and fine-tuning them to produce the most accurate reconstruction is a more efficient process. This is a closed-loop optimization technique in which the aim is to select the best parameters to fit the synthetic speech as closely as possible to the original speech.
The block diagram of a closed-loop encoder is shown in the figure. The principle is known as analysis-by-synthesis since the signal is synthesized during encoding for analysis purposes.
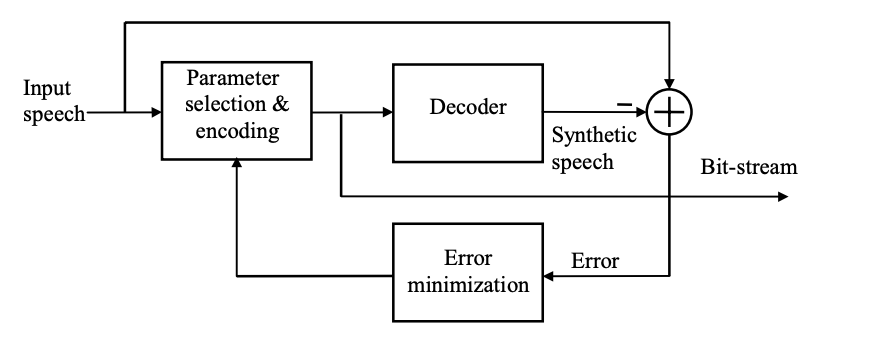
Fig 1: Block diagram showing an encoder based on the analysis-by-synthesis principle
Theoretically, all of the speech coder's parameters can be optimized together to achieve the best result. However, due to the computation needed, this method is too complicated. In practice, only a subset of parameters is chosen for closed-loop optimization, with the remaining parameters calculated using an open-loop method. The CELP coder is based on the analysis-by-synthesis theory, which involves selecting excitation sequences from a codebook using a closed-loop process. The filter coefficients, for example, are calculated in an open-loop fashion.
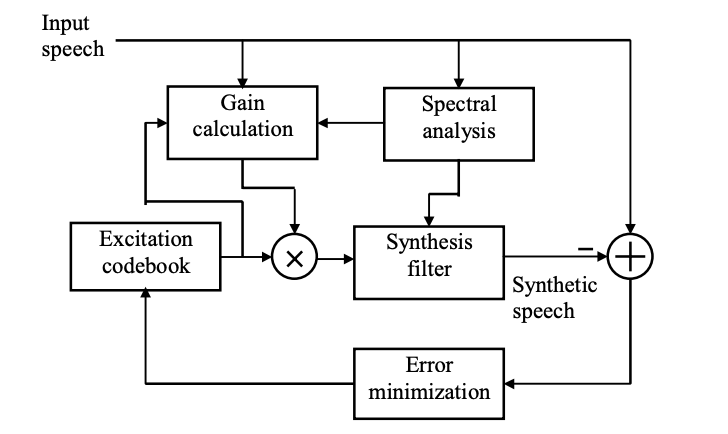
Fig 2: Block diagram showing the key components of a CELP encoder
A simplified block diagram of the CELP encoder is shown in Figure.
To select the final excitation sequence, a widely used error criterion, such as the amount of squared error, can be used; thus, waveform matching in the time domain is performed, resulting in partial preservation of phase information. The compressed bit-stream is then formed by encoding the excitation sequence and other parameters. The bit-rate of the coding scheme is affected by the length of the analysis block or frame.
Key takeaway:
CELP is an analysis-by-synthesis process in which the excitation signal is chosen and added to the synthesis filters using a closed-loop search technique. The distortion is calculated after comparing the synthesized waveform to the original speech section, and the procedure is repeated for all excitation code vectors stored in a codebook. The decoder receives the index of the "best" excitation sequence and retrieves the excitation code vectors from a codebook similar to the encoder's.
Perceptual Weighting
The CELP encoder is based on an analysis-by-synthesis loop, as shown in Figure, where the machine feature of the formant synthesis filter is
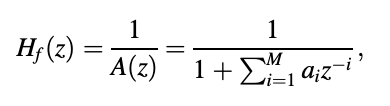
The machine function of the formant analysis filter is denoted by A(z). Assume that the excitation codebook is L bytes in size, containing L excitation code vectors in total. For each short segment of input expression, the encoder will run through the loop L times, with a mean-squared error value determined after each pass. At the end, the excitation code vector with the lowest error is chosen.
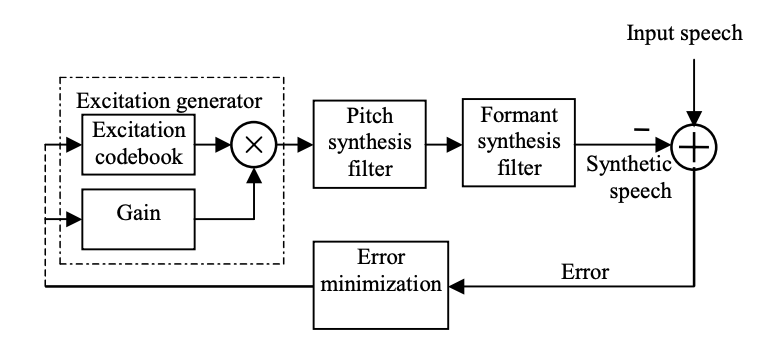
Fig 3: Analysis-by-synthesis loop of a CELP encoder
The length of the speech section under consideration determines the size of the code vector; for most CELP coders, the length is equal to the subframe length. For example, the FS1016 coder (next chapter) has a subframe of 60 samples (7.5 ms) and a codebook size of L = 512. As a result, the excitation codebook can be thought of as a 512 X 60 matrix.
The human auditory system's masking phenomenon can be investigated to provide a more acceptable error measure. It is well understood that in frequency regions where speech has a lot of energy, we can handle a lot more noise. As a result, the energy of noise components in these regions may be higher than that of noise components in low-energy regions without increasing perceptual distortion.
In other words, high-energy speech signals can cover or ‘‘mask" a proportionately higher amount of noise, while low-energy speech signals can cover or ‘‘mask" a proportionately lower amount of noise. As a result, the amount of noise at the peaks of a standard speech continuum can be greater than the amount of noise at the valleys. Filtering the error signal via a weighting filter before minimization is an easy way to monitor the noise spectrum
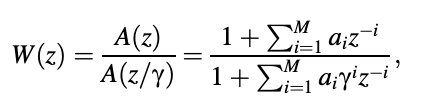
where 𝛾 is a constant in the range [0, 1]. Figure shows the location of this filter inside the loop. In any frequency field, the constant 𝛾 determines how much the error is de-emphasized.
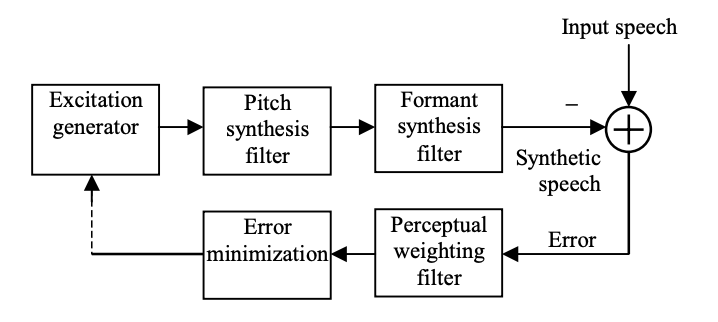
Fig 4: Analysis-by-synthesis loop of a CELP encoder with perceptual weighting.
Encoder Operation
Figure depicts a block diagram of a generic CELP encoder. This encoder is very basic and is only meant to be used as an example. The operation of various standard CELP coders is then discussed. The encoder functions like this:
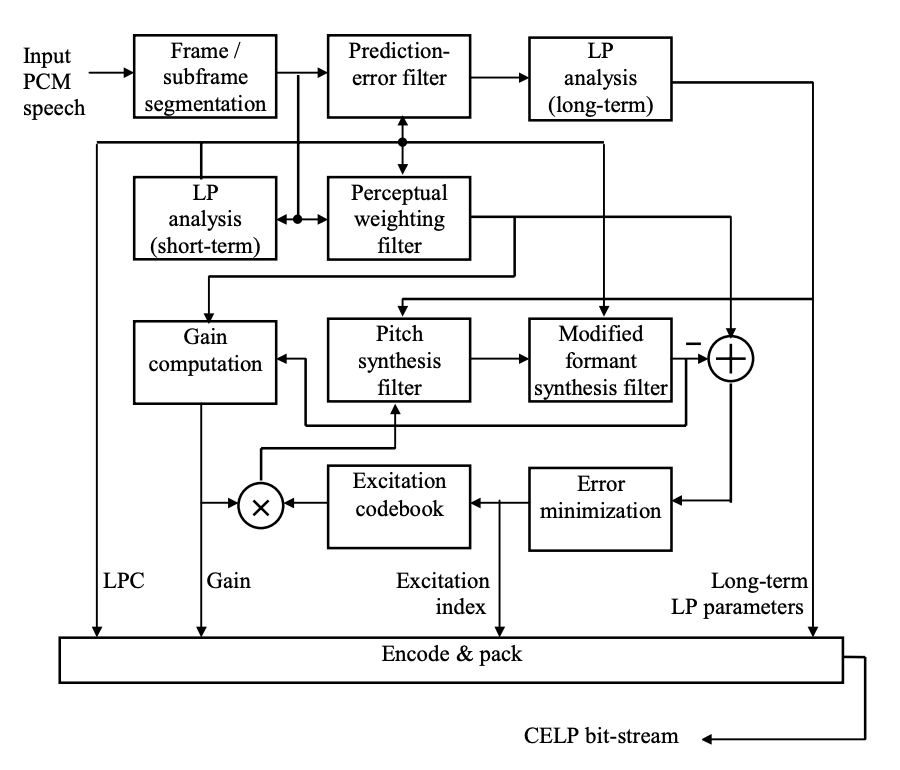
Fig 5: Block diagram of a generic CELP encoder
● Frames and subframes are generated from the input speech signal. A common scheme is to use four subframes in one frame. The frame is normally 20 to 30 milliseconds long, while the subframe is 5 to 7.5 milliseconds long.
● To calculate the LPC, each frame is subjected to a short-term LP analysis. After that, each subframe is subjected to long-term LP analysis. The initial expression, or pre-emphasized speech, is usually the input to short-term LP analysis; the (short-term) prediction error is often the input to long-term LP analysis. After this step, you'll know the coefficients of the perceptual weighting filter, pitch synthesis filter, and modified formant synthesis filter.
● It is now possible to evaluate the excitation series. Each excitation code vector is the same length as the subframe, so an excitation codebook search is done once per subframe. The search procedure starts with the development of an ensemble of filtered excitation sequences with corresponding gains; for each sequence, the mean-squared error (or total of squared error) is computed, and the code vector and gain associated with the lowest error are chosen.
● The CELP bit-stream encodes, packs, and transmits the index of excitation codebook, gain, long-term LP parameters, and LPC.
Decoder Operation
Figure shows a block diagram of the CELP decoder. It unpacks and decodes various parameters from the bitstream, which are then guided to the appropriate block in order to synthesize expression. To improve the efficiency of the resulting signal, a post filter is applied at the top.
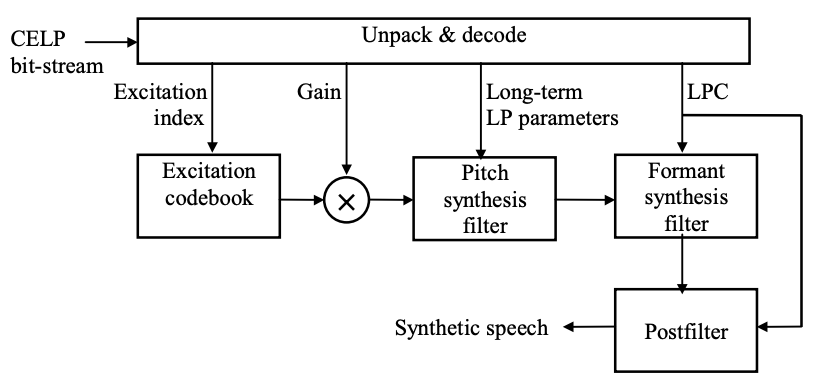
Fig 6: Block diagram of a generic CELP decode
Key takeaway:
The most computationally intensive aspect of CELP coding is the search for excitation codebooks. Many ideas have been proposed and tested over the years in relation to the subject, all with the goal of speeding up the search process without compromising the production quality. The search procedure is defined using a precise mathematical framework.
Preliminaries
A step-by-step method for searching an excitation codebook is detailed below.
2. In the excitation codebook, for each code vector:
● Calculate the optimal gain (described later) and use that value to scale the code vector.
● Apply the pitch synthesis filter to the scaled excitation code vector.
● Apply the modified formant synthesis filter to the output of the pitch synthesis filter.
● Subtract the perceptually filtered input speech from the output of the modified formant synthesis filter; the result is a sequence of errors.
● Calculate the error sequence's energy.
3. On the input subframe, the index of the excitation code vector associated with the lowest error energy is saved as information.
For each input subframe, the process is repeated. Exploring the redundancies in the search loop will help to increase computational performance. Significant computational savings can be achieved by decomposing the filters' responses into zero-state and zero-input components.
A one-tap pitch synthesis filter is linked in cascade with the modified formant synthesis filter in the system under consideration, as shown in Figure. The system's difference equations are
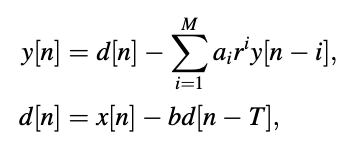
Where,
M = Prediction order (short-term),
ai = LPC (short-term),
b = Long-term gain,
T = Pitch period.
Equations are used to compute the filters’ outputs.
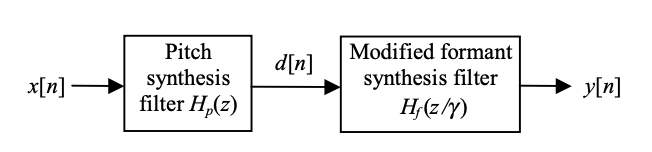
Fig 7: Cascade connection of pitch synthesis filter and modified formant synthesis filter.
State-Save Method
The difference equations are applied in the following way (r > 0) to each of the finite-length input subframes xr[n], n = 0 to N - 1:
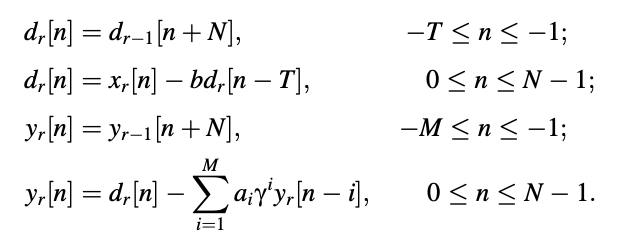
Key takeaway:
This approach calculates the total response by estimating the zero-input and zero-state responses separately. The total response is made up of these two replies. Figure depicts the signals that are involved.
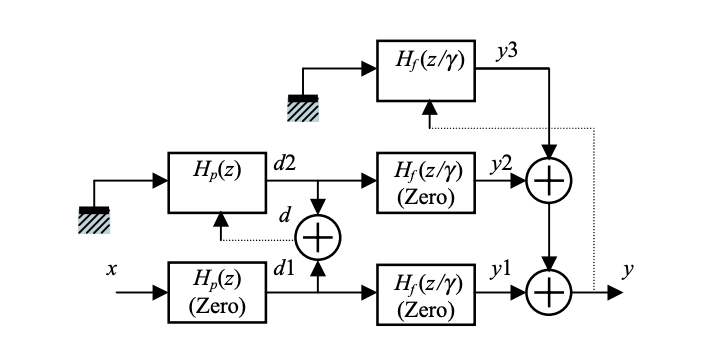
Fig 8: Block diagram showing the signals involved in the zero-input zero-state method for the computation of output signal from a cascade connection of pitch synthesis filter and modified formant synthesis filter
The following sections go into the specifics of each signal.
● Zero-state response of pitch synthesis filter (d1) :
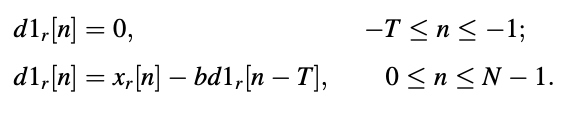
Because of the zero-state condition, the first T samples can be computed without the product in the above equation. As a result, the equation can be rewritten as
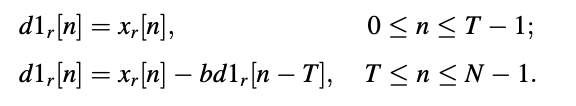
T < N is assumed in this case. The zero-state answer is equal to the input signal if T ≥ N.
● Zero-input response of pitch synthesis filter (d2):
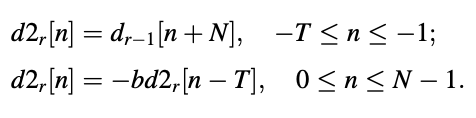
● Total response of pitch synthesis filter (d ):
dr[n] = d1r[n] + d2r[ n] , 0 ≤ n ≤ N - 1,
● Total zero-state response: zero-state response of the pitch synthesis filter, filtered by the formant synthesis filter in zero-state (y1):
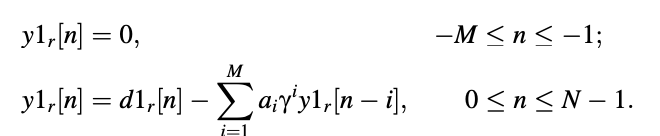
● Zero-input response of pitch synthesis filter, filtered by the formant synthesis filter in zero-state (y2):
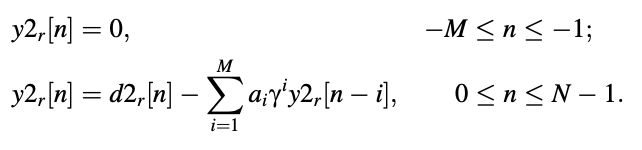
● Zero-input response of formant synthesis filter (y3):
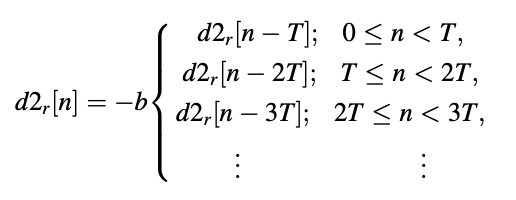
● Total response (formant synthesis filter):
yr[n] = y1r[n] + y2r[n] + y3r[n] , 0 ≤ n ≤ N - 1:
Key takeaway:
The pitch synthesis filter's operation is complicated by the way the zero-input response d2 (12.4) is described.
The adaptive codebook definition was created as a modification to reduce complexity while maintaining the same principle of minimizing the weighted difference through a closed-loop analysis-by-synthesis approach. To put it another way, any ‘‘cheating" is used to get around the computational barrier. The operation of the pitch synthesis filter is redefined in this proposal.
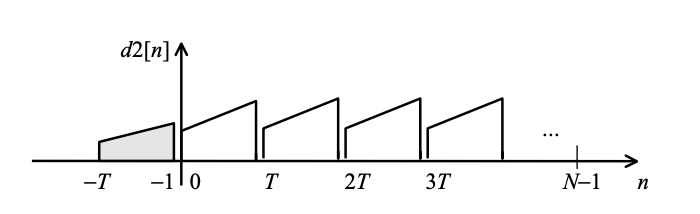
For a standard case of T < N, the effect is shown in Figure. The adaptive codebook concept obviously differs from the original pitch synthesis filters. Both definitions are correct for T ≥ N; however, for T < N, the adaptive codebook answer is generated by a periodic extension of the past multiplied by the long-term benefit.
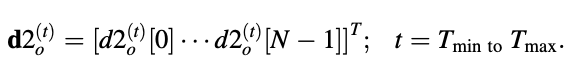
Fig 9: Extracting a code vector from the adaptive codebook when T < N
By ‘‘cheating" in this way, the current subframe's zero-input response (with unit scaling) is totally determined from history, removing the burden associated with the higher power of b found in the standard pitch synthesis filter definition. When b = 1, the two meanings are, of course, identical. According to this reformulation, b can be solved by using simple procedures to check through the values of T.
When T < N, the adaptive codebook solution has the drawback of maintaining the same amplitude of pitch pulses in a subframe from one pulse to the next. However, it has been noted that the technique is subjectively quite close to the pitch synthesis filter's initial formulation. In other words, using the adjusted approach has no impact on subjective consistency.
Operation of the Adaptive Codebook
Since the search method for the optimum pitch time can be thought of as the evaluation of a codebook with overlapping code vectors, the formulation is called an adaptive codebook. This means that neighboring code vectors share samples, which are indexed by the pitch length T. Since it is changed from subframe to subframe, the codebook is adaptable.
Consider the adaptive codebook's structure, as shown in Figure. Tmax is the maximum value of the pitch duration, so the codebook is defined as a 1-D array of Tmax components. The elements of the codebook are now denoted as d[-Tmax] to d[-1], and the subframe index r has been removed.
Code vectors derived from this codebook are denoted by
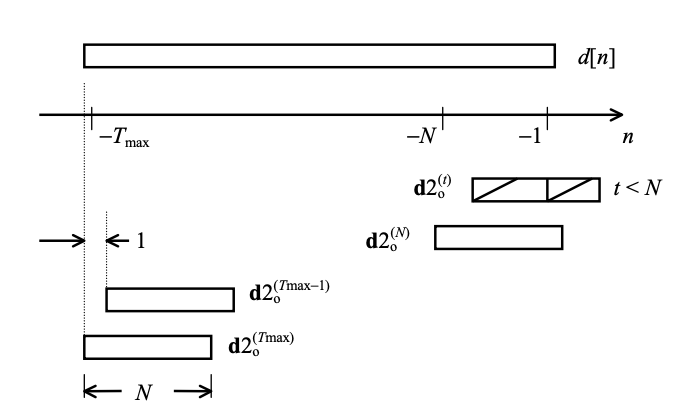
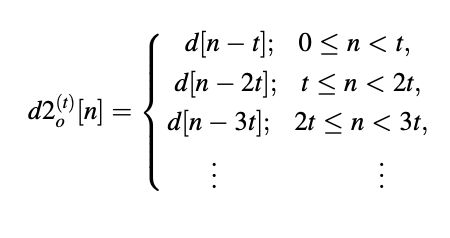
Fig 10: Illustration of the structure of an adaptive codebook
The elements of the code vector can now be defined as follows using the above equation:
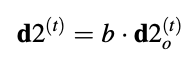
if t < N, and
d20(t)[n] = d[n - t]
if t < N, for 0 ≤ n ≤ N - 1.As a result, the codebook can be checked for all index t in order to find the best code vector d2o(t) and the best long-term benefit b. The scaled code vector is created once these variables are identified.
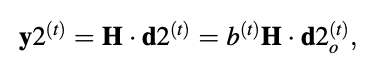
represents the optimal zero-input response of the modified pitch synthesis filter.
Key takeaway:
Here, we study the procedure to search for the optimal adaptive code vector,
the use of fractional delay, and encoding of related parameters.
Integer Pitch Period
The adaptive codebook is searched in a closed-loop analysis-by-synthesis manner, where the index of the best code vector, t = Tmin, Tmin + 1, ..., Tmax, is located. This index is given seven bits, resulting in 27 = 128 values ranging from Tmin = 20 to Tmax = 147. The method for searching the adaptive codebook follows the same principles as the excitation codebook search. Only the highlights are provided; readers are left to check the equations' validity on their own.
The updated formant synthesis filter's zero-state answer is given by
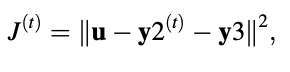
H denotes the synthesis filter's impulse response matrix. The following is a rewrite of the equation:
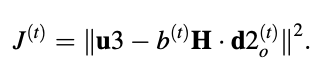
which is our goal for cost-cutting. Identifying
u3 = u - y3;
We have,
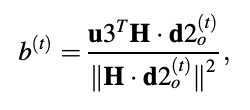
It can be demonstrated that the best adaptive codebook gain for minimizing is
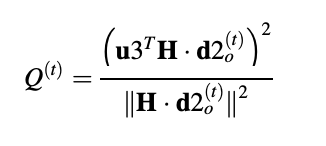
and the best codebook index is the one that gives you the most bang for your buck.
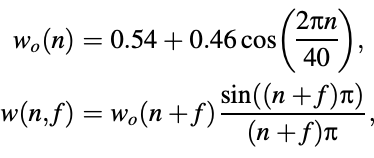
from Tmin to Tmax for t = Tmin to Tmax Recursive convolution can be used to achieve efficient computation since the adaptive codebook is basically an overlapping codebook with unit transfer.
Fractional Pitch Period
Fractions Pitch, its use eliminates both reverberant distortions caused by pitch multiplication and the roughness of speakers with short pitch periods. Noise is reduced in synthetic speech as output associated with long-term prediction improves, reducing the noisy stochastic excitation portion.
The FS1016 specifies an interpolation* technique based on a 40-point Hamming windowed sinc function defined as follows to obtain the adaptive code vector with fractional delay:
for n = 20, -19, ... , 19, with f being the fractional part of the pitch period.
Subframe Encoding Strategy
The pitch length is encoded by FS1016 using different numbers of bits, depending on the location of the subframe. 8 bits are assigned to the first and third subframes, and the encoding scheme is the same as before. However, only 6 bits are used in the second and fourth subframes. These 6 bits reflect a relative change in pitch time compared to the previous subframe, varying from 31 codes lower to 32 codes higher, with both integer and fractional values taken into account.
Since pitch intervals of adjacent subframes do not vary dramatically in most cases, the scheme provides higher encoding efficiency (smaller number of bits) and lowers computational load (shorter search range); the benefits come with marginal loss in synthetic speech quality.
Key takeaway:
Delay is a significant consideration for real-time two-way conversations, and it is described as the time it takes for sound to move from the speaker to the listener. The ability to maintain a conversation is compromised when there is an unnecessarily long pause, such as more than 150 milliseconds.
Because of the time it takes to understand the other party is speaking, the parties tend to interrupt or ‘‘talk over" each other. When the delay is high enough, conversations degrade to half-duplex mode, with only one direction of communication taking place at a time; hence, the lower the delay, the better.
Low delay is also ideal in traditional telephone networks because delay exacerbates echo problems: the longer an echo is delayed, the more noticeable and distracting it becomes to the talker. Despite the fact that echo cancelers are commonly used, high delay makes echo cancellation more difficult.
BASIC OPERATIONAL PRINCIPLES
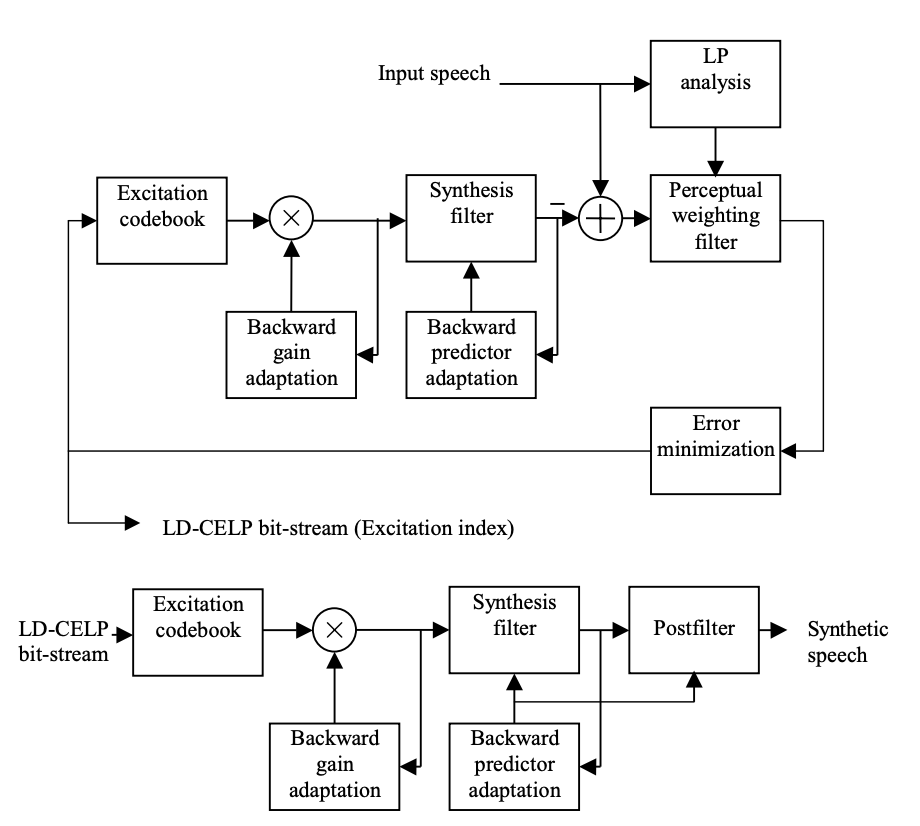
We're ready to move on to the basic operating concepts now that we've gone through the most distinguishing features of LD-CELP in the previous portion. To begin the encoding process in LD-CELP, only five samples are needed. Only the excitation signal, on the other hand, is transmitted; the predictor coefficients are modified using LP analysis on previously quantized expression.
As a result, the LD-CELP coder is essentially a backward adaptive variant of the CELP coder. The nature of CELP is preserved, namely the analysis-by-synthesis codebook quest. The LD-CELP encoder and decoder have the following general structures.
The basic operational concept is the same as the traditional CELP algorithm, with the exception that only the index to the excitation codebook is sent. The LD-CELP algorithm's operation can be summarized as follows:
● Speech samples are partitioned into frames and subdivided into subframes, much as in traditional CELP. Each frame in LD-CELP contains 20 samples, divided into four subframes of five samples each. There is no need to buffer an entire frame before processing LP analysis since it is done in a backward adaptive manner. Before the encoding process starts, only one subframe (five samples) must be saved.
● Ten linear prediction coefficients obtained from the original speech data make up the perceptual weighting filter. Once per frame, the filter is changed. The current frame's coefficients are calculated using samples from previous frames.
● A 50th-order AR process is described by the synthesis filter. Its coefficients are derived from previous frames' synthetic speech results. Once per frame, the filter is changed. The current frame's zero-input answer can be calculated using the known initial conditions.
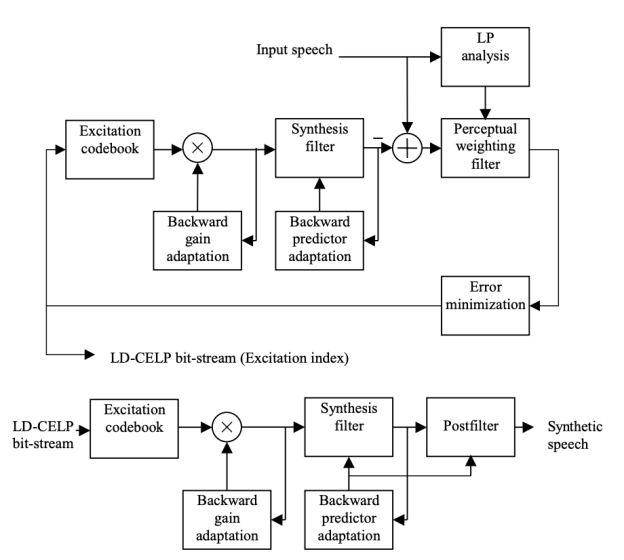
Fig 11: LD-CELP encoder (top) and decoder (bottom)
● Per subframe, the excitation gain is modified using a tenth-order adaptive linear predictor operating in the logarithmic-gain domain. This predictor's coefficients are modified once per frame, and the LP analysis method is performed on gain values from previous subframes.
● The excitation sequence is searched once per subframe, with the search process involving the generation of an ensemble of filtered sequences, with each excitation sequence serving as an input to the formant synthesis filter to produce an output sequence. The excitation sequence with the lowest final error is chosen.
● The original conditions are restored in the decoder. Filtering the indicated excitation sequence through the filter without any perceptual weighting produces synthetic expression. There is no need to transmit the excitation gain or the LPCs because they are backward adaptive. A post filter can be used to improve the output speech quality even further.
Key takeaway:
Another effort to reduce the computational expense of regular CELP coders was Algebraic CELP, or ACELP. Many ACELP-related specifications are based on the work of previous CELP coders. The word "algebraic" refers to the development of excitation code vectors using basic algebra or mathematical laws, such as addition and shifting.
Because of the method, there is no need to physically store the entire codebook, which saves a lot of memory. Adoul and Lamblin [1987] and Adoul et al. [1987] were the first to present the original ideas, two years after Schroeder and Atal [1985]. Many researchers have perfected it, resulting in at least five standardized coders:
● ITU-T G.723.1 Multipulse Maximum Likelihood Quantization (MP-MLQ)/ ACELP (1995).
● ITU-T G.729 Conjugate Structure (CS)–ACELP (1995).
● TIA IS641 ACELP (1996)
● ETSI GSM Enhanced Full Rate (EFR) ACELP (1996).
● ETSI Adaptive Multirate (AMR) ACELP (1999).
The ACELP definition has a significant impact on the direction of speech coding development; understanding its structure is needed to comprehend some of the field's most powerful trends.
Key takeaway:
References:
2. 2. “Speech Coding Algorithms: Foundation and Evolution of Standardized Coders”, W.C. Chu, Wiley Inter science, 2003.