Module -1

Basic Probability

1.1  Probability Spaces

A probability space is a three-tuple (S, F, P) in which the three components are

1. Sample space: A nonempty set S called the sample space, which represents           all possible outcomes.
2. Event space: A collection F of subsets of S, called the event space.
3. Probability function: A function P : FR, that assigns probabilities to the events in F.

DEFINITIONS:

1. Die: It is a small cube. Dots (number) are marked on its faces. Plural of the die is dice. On throwing a die, the outcome is the number of dots on its upper face.

2. Cards: A pack of cards consists of four suits i.e. Spades, Hearts, Diamonds and Clubs. Each suit consists of 13 cards, nine cards numbered 2, 3, 4, ..., 10, an Ace, a King, a Queen and a Jack or Knave. Colour of Spades and Clubs is black and that of Hearts and Diamonds is red.

Kings, Queens and Jacks are known as facecards.

3. Exhaustive Events or Sample Space: The set of all possible outcomes of a single performance of an experiment is exhaustive events or sample space. Each outcome is called a sample point.

In case of tossing a coin once, S = (H, T) is the sample space. Two outcomes - Head and Tail

- constitute an exhaustive event because no other outcome is possible.

4. Random Experiment: There are experiments, in which results may be altogether different, even though they are performed under identical conditions. They are known as random experiments. Tossing a coin or throwing a die is random experiment.

5. Trial and Event: Performing a random experiment is called a trial and outcome is termed as event. Tossing of a coin is a trial and the turning up of head or tail is an event.

6. Equally likely events: Two events are said to be ‘equally likely’, if one of them cannot be expected in preference to the other. For instance, if we draw a card from well-shuffled pack, we may get any card. Then the 52 different cases are equally likely.

7. Independent events: Two events may be independent, when the actual happening of one does not influence in any way the probability of the happening of the other.

8. Mutually Exclusive events: Two events are known as mutually exclusive, when the occurrence of one of them excludes the occurrence of the other. For example, on tossing of a coin, either we get head or tail, but not both.

9. Compound Event: When two or more events occur in composition with each other, the simultaneous occurrence is called a compound event. When a die is thrown, getting a 5 or 6 is a compound event.

10. Favourable Events: The events, which ensure the required happening, are said to be favourable events. For example, in throwing a die, to have the even numbers, 2, 4 and 6 are favourable cases.

11. Conditional Probability: The probability of happening an event A, such that event B has already happened, is called the conditional probability of happening of A on the condition that B has already happened. It is usually denoted by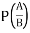

12. Odds in favour of an event and odds against an event: If number of favourable ways = m, number of not favourable events = n

(i) Odds in favour of the event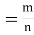

(ii) Odds against the event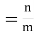

13. Classical Definition of Probability. If there are N equally likely, mutually, exclusive and exhaustive of events of an experiment and m of these are favourable, then the probability of the happening of the event is defined as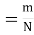

Consider Example1:In poker, a full house (3 cards of one rank and two of another, e.g. 3 fours and 2 queens) beats a flush (five cards of the same suit).

A player is more likely to be dealt a flush than a full house. We will be able to precisely quantify the meaning of “more likely” here.

Example2:A coin is tossed repeatedly.

Each toss has two possible outcomes:

Heads (H) or Tails (T)

Bothequally likely. The outcome of each toss is unpredictable; so is the sequence of H and T.

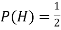However, as the number of tosses gets large, we expect that the number of H (heads) recorded will fluctuate around of the total number of tosses. We say the probability of aH is , abbreviated by . Of course  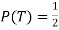 also

Example3:

If 4 coins are tossed, what is the probability of getting 3 heads and 1 tail?

NOTES:

• In general, an event has associated to it a probability, which is a real number between 0 and 1.

• Events which are unlikely have low (close to 0) probability, and events which are likely have high (close to 1) probability.

• The probability of an event which is certain to occur is 1; the probability of an impossible event is 0.

1.2  Conditional Probability

Let Aand Bbe two events of a sample space Sand let 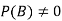. Then conditional probability of the event A, given B, denoted by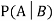is defined by –

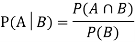
Theorem:If the events Aand Bdefined on a sample space S of a random experiment are independent, then

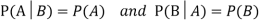
Example1:A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.

SOLUTION:We consider the following events:

A: Selected item comes from A.

B: Selected item comes from B.

D: Selected item is defective.

We are looking for 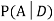. We know:

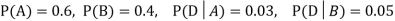
Now,

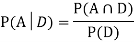
So we need

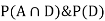
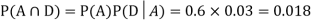
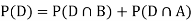
Since, D is the union of the mutually exclusive events 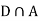and 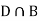(the entire sample space is the union of the mutually exclusive events A and B)

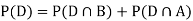
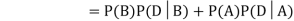
Example2:Two fair dice are rolled, 1 red and 1 blue. The Sample Space is

S = {(1, 1),(1, 2), . . . ,(1, 6), . . . ,(6, 6)}.Total -36 outcomes, all equally likely (here (2, 3) denotes the outcome where the red die show 2 and the blue one shows 3).

(a) Consider the following events:

A: Red die shows 6.

B: Blue die shows 6.

Find , and .

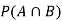Solution: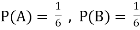

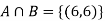
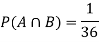
NOTE: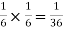so 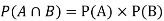for this example. This is not surprising - we expect A to occur in of cases. In of these cases i.e. in 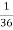of all cases, we expect B to also occur.

(b) Consider the following events:

C: Total Score is 10.

D: Red die shows an even number.

Find 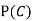, 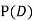and .

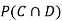Solution: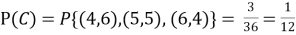

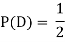
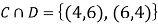
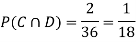
NOTE: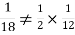so,.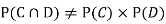

Why does multiplication not apply here as in part (a)?

ANSWER: Suppose C occurs: so the outcome is either (4, 6), (5, 5) or (6, 4). In two of these cases, namely (4, 6) and (6, 4), the event D also occurs. Thus

Although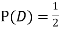 , the probability that D occurs given that C occurs is .

We write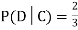, and call 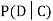the conditional probability of D given C.

NOTE: In the above example

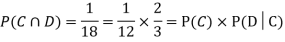
Example3:Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball drawn is red find the probability that it is drawn from the first urn.

Solution:

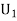:The ball is drawn from urnI.

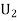: The ball is drawn from urnII.

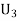: The ball is drawn from urnIII.

R:The ball is red.

We have to find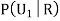

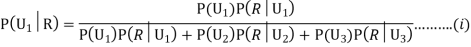
Since the three urns are equally likely to be selected

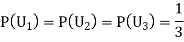
Also,

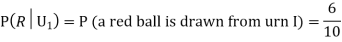
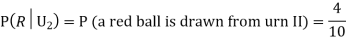
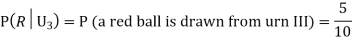
From (i), we have

1.3  Independence: Discrete Random Variables

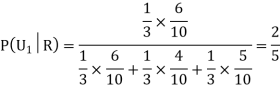
Independence:

Two events A, B ∈ are statistically independent iff

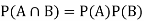
(Two disjoint events are not independent.)

Independence implies that

Knowingthat outcome is in B does not change your perception of the outcome’s being in A.

1.4  Random Variable

It is a real valued function which assign a real number to each sample point in the sample space.

Example: 1.Tossing a fair coin thrice then-

Sample Space(S) = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

2. Roll a dice

Sample Space(S) = {1,2,3,4,5,6}

Discrete Random Variable:

A random variable which takes finite or as most countable number of values is called discrete random variable.

Example: 1. No. Of head obtained when two coin are tossed.

2. No. Of defective items in a lot.

1.5 The Multinomial Distribution

1. This distribution can be regarded as generalisation of binomial distribution.
2. Where there are more than two mutually outcomes of a trial, the observations lead to multinomial distribution.
3. Suppose E1,E2,E3….EK are mutually exclusive and exhaustive outcomes of a trial with respect probabilities P1,P2,P3….PK

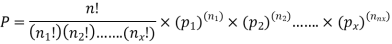
Example1:

You are given a bag of marble. Inside the bag are 5 red marble, 4 white marble, 3 blue marble. Calculate the probability that with 6 trials you choose 3 marbles that are red, 1 marble that is white and 2 marble is blue. Replacing each marble after it is chosen.

Solution:

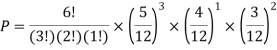
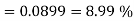
Example2:

You are randomly drawing cards from an ordinary deck of cards. Every time you pick one you place it back in the deck. You do this 5 times. What is the probability of drawing 1 heart, 1 spade, 1club, and 2 diamonds?

Solution:

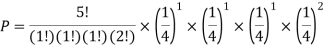
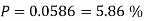
Example3:

A die weighed or loaded so that the number of spots X that appear on the up face when the die is rolled has pmf

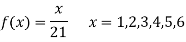
If this loaded die is rolled 21 times. Find the probability of rolling one one, two twos, three threes, four fours, five fives, six sixes.

Solution:

1.6 Poisson Approximation to the Binomial Distribution:

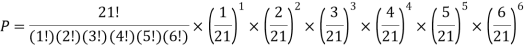
The Binomial distribution can be approachedfine by Poisson when n is big and p is small with np < 10, as specified above. This is correctsince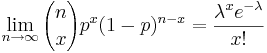, where λ = np.

Example

A plantplaces biscuits into boxes of 100. The probability that a biscuit is cracked is 0.03. Find the probability that a box contains 2 cracked biscuits

Solution

This is a binomial distribution by means of n = 100 besides p = 0.03.

These standards are external the range of the counters and include lengthy calculations.

Using the Poisson estimate (test: np = 100 x 0.3 = 3, which is less than 5)

Let X be the random variable of the number of cracked biscuits

The mean λ = np = 100 × 0.3 = 3

P(X = 2) = 0.224 (from counters)

The probability that a box contains two broken biscuits is 0.224.

Example

As in the “100 year flood” example above, nn is a large number (100) and pp is a small number (0.01). Plugging into the equation from above P(x=1)P(x=1) yields

P(X=1)=(1001)×0.011×(1−0.01)100−1=100×0.01×0.3697296=0.3697296 P(X=1)=(1001)×0.011×(1−0.01)100−1=100×0.01×0.3697296=0.3697296

The consequence is very close to the result got above dpois(x = 1,lambda = 1) =0.3678794=0.3678794. The suitable Poisson distribution is the one whose mean is the same as that of the binomial circulation; that is, λ=npλ=np, which in our example is λ=100×0.01=1λ=100×0.01=1

N=1134, p=0.015, x=20

Using binomial PMF

1.7 Bernoulli trials

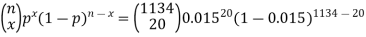
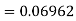
A random experiment whose results are of only two types, for example, success S and failure F, is a Bernoulli test. The probability of success is taken as p, while the probability of failure is q = 1 - p. Consider a random experiment of items in a sale, either sold or not sold. An item produced may be defective or non-defective. An egg is boiled or unboiled.

A random variable X will have the Bernoulli distribution with probability p if its probability distribution is

P(X = x) = px (1 – p)1−x, for x = 0, 1 and P(X = x) = 0 for other values of x.

Here, 0 is failure and 1 is success.

Conditions for Bernoulli tests

1. A finite number of tests.

2. Each trial must have exactly two results: success or failure.

3. The tests must be independent.

4. The probability of success or failure must be the same in each test.

Example:

Problem 1:

If the probability that a light bulb is defective is 0.8, what is the probability that the light bulb is not defective?

Solution:

Probability that the bulb is defective, p = 0.8

Probability that the bulb is not defective, q = 1 - p = 1 - 0.8 = 0.2

Problem 2:

10 coins are tossed simultaneously where the probability of getting heads for each coin is 0.6. Find the probability of obtaining 4 heads.

Solution:

Probability of obtaining the head, p = 0.6

Probability of obtaining the head, q = 1 - p = 1 - 0.6 = 0.4

Probability of obtaining 4 of 10 heads, P (X = 4) = C104 (0.6) 4 (0.4) 6P (X = 4) = C410 (0.6) 4 (0.4) 6 = 0.111476736

Problem 3:

In an exam, 10 multiple-choice questions are asked where only one in four answers is correct. Find the probability of getting 5 out of 10 correct questions on an answer sheet.
Solution:

Probability of obtaining a correct answer, p = 1414 = 0.25

Probability of obtaining a correct answer, q = 1 - p = 1 - 0.25 = 0.75

Probability of obtaining 5 correct answers, P (X = 5) = C105 (0.25) 5 (0.75) 5C510 (0.25) 5 (0.75) 5 = 0.05839920044

Sum of n independent random variables

We discussed earlier how to derive the distribution of the sum of two independent random variables. How do we obtain the distribution of the sum of more than two mutually independent random variables? Suppose, ..., they are mutually independent random variables and leave their sum: the distribution of can be derived recursively, using the results for sums of two previous random variables:

1. First, define and calculate the distribution of;

2. Then define and calculate the distribution of;

3. And so on, until the distribution of

Exercises solved

Below you can find some exercises with explained solutions.

Exercise 1

Both a uniform random variable with a probability density function and support and an exponential random variable, independent of, with a probability density function and support Derive the probability density function from the sum

Solution

The support of is When, the probability density function of is Therefore, the probability density function of is

Exercise 2

Let be a discrete random variable with support mass function and probability and another discrete random variable, independent of, with support mass function and probability Derive the probability mass function from the sum

Solution

The support of is the probability mass function of, evaluated in is evaluated in, is evaluated in, is evaluated in, therefore, the probability mass function is

1.8 Expectation of Discrete Random Variables, Moments

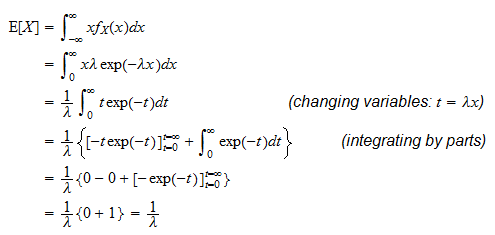
Definition

Expected value for a discrete random variable is ;

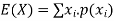
Expected value for a continuous random variable is

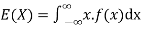
The mean describes where the probability distribution is centered.

The law of the sum of variances is an expression for the variance of the sum of two variables. If the variables are independent, and therefore Pearson's r = 0, the following formula represents the variance of the sum and the difference of the variables X and Y: note that you add the variances for X + Y and X - AND.

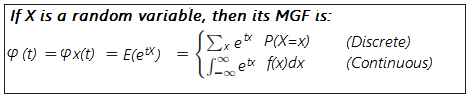
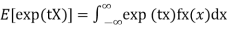
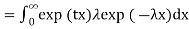
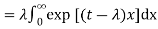
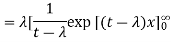
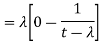
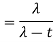
• Example: Find the MGF for e-x.

Solution:
Step 1: Plug e-x in for fx(x) to get: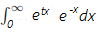
 

• Example: Find E(X3) using the MGF (1-2t)-10.

Step 1: Find the third derivative of the meaning (the list above defines M′′′(0) as existence equal to E(X3); earlier you can estimate the derivative at 0, you first need to find it):
M′′′(t) = (−2)3(−10)(−11)(−12)(1 − 2t)-1

The correlation coefficient

The correlation coefficient, indicated by r, tells us how much data on a scatter diagram falls along a straight line. The closer the absolute value of r is to one, the better the data is described using a linear equation. If r = 1 or r = -1, the dataset is perfectly aligned. Datasets with r values   close to zero show poor or absent straight relationship

1.9 Variance Of A Sum, Correlation Coefficient, Chebyshev's Inequality

Correlation coefficient formula

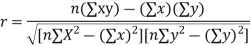
1. Due to long calculations, it is better to calculate r with the use of a calculator or statistical software. However, it is always useful to try to understand what the calculator does during the calculation. The following is a process for calculating the correlation coefficient primarily by hand, with a calculator used for routine arithmetic steps.
2. Steps for calculation r
3. We will start by listing the steps to calculate the correlation
4. Coefficient. The data we are working with is paired data, each of which will be indicated by (xi, yi).
5. 1. Let's start with some preliminary calculations. The amounts of these calculations will be used in the later stages of our calculation of r:
6. 1. Calculate x̄, the average of all the first coordinates of the xi data.
7. 2. Calculate ȳ, the average of all the second coordinates of the data
8. 3. Yi.
9. 4. Calculate s x the sample standard deviation of all the first coordinates of the xi data.
10. 5. Calculate the sample standard deviation of all the second coordinates of the data yi.
11. 2. Use the formula (zx) i = (xi - x̄) / s x and find a standardized value for each xi.
12. 3. Use the formula (zy) i = (yi - ȳ) / s y and find a standardized value for each yi.Multiply corresponding standardized values: (zx)i(zy)i
13. Add the products from the last step together.
14. Divide the sum from the previous step by n – 1, where n is the total number of points in our set of paired data. The result of all of this is the correlation coefficient r.

• This process is not difficult and each step is quite routine, but the compilation of all these steps is quite complicated. Calculating the standard deviation is quite tedious on its own. But calculating the correlation coefficient involves not just two standard deviations, but a multitude of other operations.

An example

• To see exactly how we get the value of r, let's look at an example. Again, it is important to note that for practical applications we would like to use our calculator or statistical software to calculate r for us.
• Let's start with a list of associated data: (1, 1), (2, 3), (4, 5), (5.7). The average of the values   of x, the average of 1, 2, 4 and 5 is x̄ = 3. We also have that ȳ = 4.
• The standard deviation of thex values   are sx = 1.83 and sy = 2.58. The following table summarizes the other calculations necessary for r. The sum of the products in the right column is 2.969848. Since there are a total of four points and 4 - 1 = 3, we divide the sum of the products by 3. This gives us a correlation coefficient of r = 2.969848 / 3 = 0.989949.

Example 2

The effect of the degree of risk on the portfolio is illustrated as follows: Portfolio risk is measured in this example when the correlation of the coefficients is -1, 1.5, -0.5, 9, + 1 when x = - 1, the risk is the lowest, the risk would be zero if the percentage of inversion in values   X1 and Xj is modified so that the standard deviation becomes 0 and x = -1.

(i)When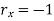

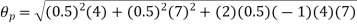
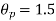
(ii)When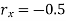

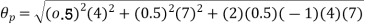
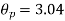
(iii)When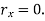

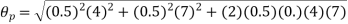
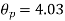
(iv)When,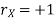

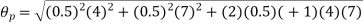
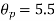
Chebyshev inequality

Chebyshev's inequality, also known as Chebyshev's theorem, makes a fairly broad but useful statement about data dispersion for almost all data distributions. This theorem states that no more than 1 / k2 of the distribution values   will be more than k standard deviations from the average. Observed in another way, 1 - (1 / k2) of the distribution values   will be within k standard deviations of the mean.

Although this equation often leads to a relatively wide range of values, it is useful in that it only requires knowledge of the mean and standard deviation, which are easily calculated from any sample or population of data. The theorem provides what might be called a worse view of the dispersion of data within any distribution of data.

Chebyshev's inequality formula

To study this theorem, we first compare the calculations with the general rule 68-95-99.7 for normal distributions. Since those numbers represent the data within the limits, we use Chebyshev inequality for the data within the limits:

Probability = 1 - (1 / k2)

Mathematically, values   less than or equal to 1 are not valid for this calculation. However, linking the k values   for 2 and 3 is relatively simple:

P (k = 2): 1 - (1/22) = 1 - 0.25 = 0.75 (75%)

P (k = 3): 1 - (1/32) = 1 - 0.11 = 0.89 (89%)

In these cases, the Chebyshev inequality states that at least 75% of the data will fall within 2 standard deviations of the mean and that 89% of the data must fall within 3 standard deviations of the average. This is less accurate than the 95% and 99.7% values   that can be used for a known normal distribution; however, the Chebshyev inequality is valid for all data distributions, not just for a normal distribution.

Problem example: A left-angle distribution has an average of 4.99 and a standard deviation of 3.13. Use the theorem to find the proportion of observations you would expect to find within two standard deviations of the average:

Step 1: Square the number of standard deviations:

22 = 4.

Step 2: Divide 1 by the answer to Step 1:

1/4 = 0.25.

Step 3: subtract step 2 from 1:

1 - 0.25 = 0.75.

At least 75% of the observations are between -2 and +2 standard deviations from the average.

That is to say:

Mean - 2 standard deviations

4.99 - 3.13 (2) = -1.27

Mean + 2 standard deviations

4.99 + 3.13 (2) = 11.25

Or between -1.27 and 11.25

Proposition Let be a random variable with finite mean and finite variance. Let (that is, it is a strictly positive real number). So, the following inequality, called Chebyshev's inequality, is true:

The proof is a direct application of the Markov inequality.

Example

Suppose we draw a random individual from a population whose members have an average income of $ 40,000, with a standard deviation of $ 20,000. What is the probability of extracting an individual whose income is less than $ 10,000 or greater than $ 70,000? Without more information about income distribution, we cannot exactly calculate this probability. However, we can use Chebyshev's inequality to calculate an upper limit. If indicating income, then it is less than $ 10,000 or more than $ 70,000 if and only if where and. The probability of this happening is:

Therefore, the probability of extracting an individual outside the income range $10,000-$70,000 is less than .

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Let  be a random variable such that

Find a lower bound to its variance.

Solution

The lower bound can be derived thanks to Chebyshev's inequality:

References

1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
2. P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
4. W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
5. N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
7. T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010