Module -3
Bivariate Distributions
A bivariate distribution, setonly, is the probability that a definite event will happen when there are 2 independent random variables in your scenario. E.g, having two bowls, individually complete with 2dissimilarkinds of candies, and drawing one candy from each bowl gives you 2 independent random variables, the 2dissimilar candies. Since you are pulling one candy from each bowl at the same time, you have a bivariate distribution when calculating your probability of finish up with specific types of candies.
Properties:
Property 1
Two random variable X and V are said to be bivariate normal, or jointly normal, if aX +bY has a normal distribution for all a, 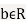
Properties 2:
Two random variable X and V are said to be standard bivariate normal distribution with correlation coefficient 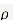 if their joint PDF is given by
if their joint PDF is given by
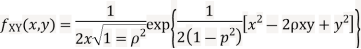
Where  . If
. If  , then we just say X and Y have the standard bivirate normal distribution.
, then we just say X and Y have the standard bivirate normal distribution.
Properties 3:
Two random variable X and V are said to be bivariate normal distribution with parameters 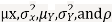 if their joint PDF is given by
if their joint PDF is given by
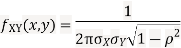
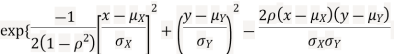
Where, 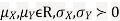 and
and 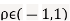 are all constants
are all constants
Properties 4:
Suppose X and Y are jointly variables with parameters 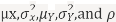 . Then given X=x,Y is normally distributed with
. Then given X=x,Y is normally distributed with
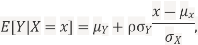
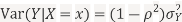
Example 1:
Let  be two independent N(0,1) random variables. Define
be two independent N(0,1) random variables. Define

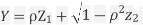
Where 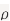 is a real number in (-1,1)
is a real number in (-1,1)
a. Show that X and Y are bivariate normal.
b. Find the joint PDF of X and Y.
c. Find 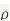 (X,Y)
(X,Y)
Sol. First, note that since  are normal and independent , they are jointly normal with the joint PDF
are normal and independent , they are jointly normal with the joint PDF
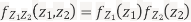
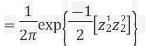
- We need to show aX+bY is normal for all
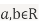 we have
we have

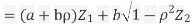
 and thus it is normal.
and thus it is normal.
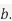 We can use the methods of transformations (Theorem 5.1) to find the joint PDF of X and Y . The inverse transformation is given by
We can use the methods of transformations (Theorem 5.1) to find the joint PDF of X and Y . The inverse transformation is given by
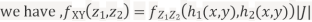

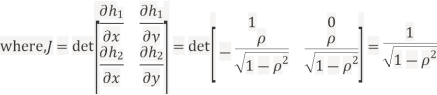
Thus we conclude that,
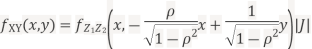
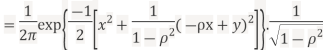
 To find
To find 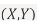 , first mode
, first mode


Therefore,



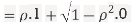
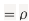
Example 2:
Let X and Y be jointly normal random variables with parameters 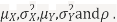 Find the conditional distribution of Y given X =x.
Find the conditional distribution of Y given X =x.
 Sol. One way to solve this problem is by using the joint PDF formula since X
Sol. One way to solve this problem is by using the joint PDF formula since X N
N 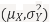 we can use
we can use
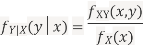
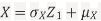
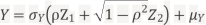
Thus given X=x, we have

And,

Since  are independent, knowing
are independent, knowing  does not provide any information on
does not provide any information on 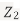 . We have shown that given X=x,Y is a linear function of
. We have shown that given X=x,Y is a linear function of 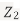 , thus it is normal. Ln particular
, thus it is normal. Ln particular
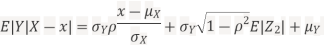
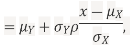

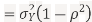
We conclude that given X=x,Y is normally distributed with mean 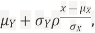 and variance
and variance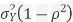
Example 3;
Let X and Y be jointly normal random variables with parameters 
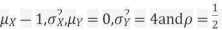
- Find
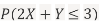
- Find
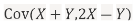
- Find
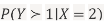
Sol. a. Since X and Y are jointly normal, the random variable V-2X+Y is normal. We have
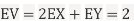


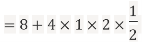
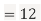
Thus, 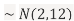 , therefore,
, therefore,
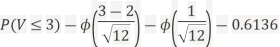
b. Note that 
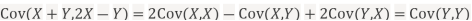
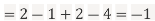
c. Using Properties, we conclude that given X=2,Y is normally distributed with
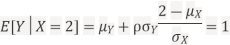
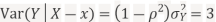
Thus,
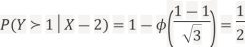
Given random variables X and Y that are defined on a probability space, the joint probability distribution for X and Y is a probability distribution that gives the probability that each of X and Y falls in any particular range or discrete set of values specified for that variable. In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to any number of random variables, giving a multivariate distribution.
The joint probability distribution can be expressed either in terms of a joint cumulative distribution function or in terms of a joint probability density function (in the case of continuous variables) or joint probability mass function (in the case of discrete variables). These in turn can be used to find two other types of distributions: the marginal distribution giving the probabilities for any one of the variables with no reference to any specific ranges of values for the other variables, and the conditional probability distribution giving the probabilities for any subset of the variables conditional on particular values of the remaining variables.
Example
A die is tossed thrice. A success is getting 1 or 6 on a toss. Find the mean and variance of the number of successes.
Sol. Probability of mean success =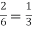
Probability of failures=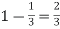
Probability of no success =Probability of all 3 failures =
Probability of one success and 2 failures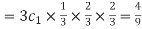
Probability of two success and one failure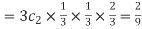
Probability of three successes 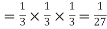
Now,
 0 1 2 3
0 1 2 3
 =8/27 4/9 2/9 1/27
=8/27 4/9 2/9 1/27
Mean,
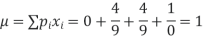
Also,
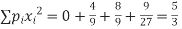
Variance,
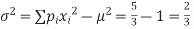
Example
The probability density function of a variate X is
X 0 1 2 3 4 5 6
P(X) k 3k 5k 7k 9k 11k 13k
(i) Find 
(ii) What will be the minimum value of k so that 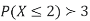 .
.
Sol.
(i) If X is a random variable, then
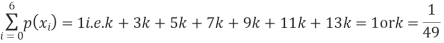
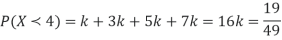

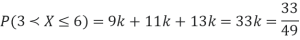
(ii) 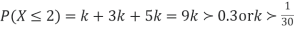
Thus minimum value of k 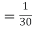
Example
A random variable X has the following probability function
x: 0 1 2 3 4 5 6 7
p(x) 0 k 2k 2k 3k 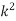
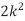
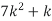
(i) Find the value of k.
(ii) Evaluate 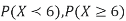
(iii) 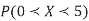
Sol. (i) If X is a random variable then
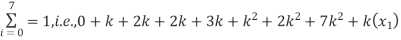
i.e. 
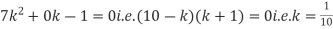
(ii) 
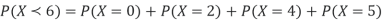
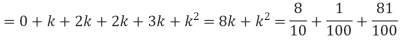

(iii)

In probability theory assumed two jointly distributed R.V. X & Y the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a precise value; in some suitcases the conditional probabilities may be stated as functions containing the unnamed x value of X as a limitation. Once together X and Yare given variables, a conditional probability is characteristically used to indicate the conditional probability. The conditional distribution differences with the marginal distribution of a random variable, which is distribution deprived of reference to the value of the additional variable.
the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a precise value; in some suitcases the conditional probabilities may be stated as functions containing the unnamed x value of X as a limitation. Once together X and Yare given variables, a conditional probability is characteristically used to indicate the conditional probability. The conditional distribution differences with the marginal distribution of a random variable, which is distribution deprived of reference to the value of the additional variable.
If conditional distribution of Y under X is a continuous distribution, then probability density function is called as conditional density function. The properties of a conditional distribution, such as the moments, are frequently denoted to by corresponding names such as the conditional mean and conditional variance.
If 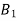 ,
, 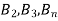 are mutually exclusive events with
are mutually exclusive events with 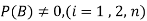 of a random experiment then for any arbitrary event
of a random experiment then for any arbitrary event 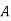 of the sample space of the above experiment with
of the sample space of the above experiment with  , we have
, we have
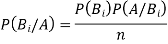
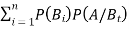 (for
(for 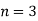 )
)
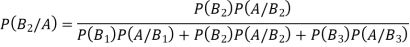
Example (1)An urn  contains 3 white and 4 red balls and an urn lI contains 5 white and 6 red balls. One ball is drawn at random from one ofthe urns and isfound to be white. Find the probability that it was drawn from urn 1.
contains 3 white and 4 red balls and an urn lI contains 5 white and 6 red balls. One ball is drawn at random from one ofthe urns and isfound to be white. Find the probability that it was drawn from urn 1.
Solution: Let 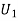 : the ball is drawn from urn I
: the ball is drawn from urn I
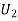 : the ball is drawn from urn II
: the ball is drawn from urn II
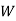 : the ball is white.
: the ball is white.
We have to find 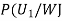
By Bayes Theorem
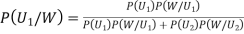 ... (1)
... (1)
Since two urns are equally likely to be selected, 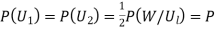 (a white ball is drawn from urn
(a white ball is drawn from urn  )
) 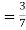
 (a white ball is drawn from urn II)
(a white ball is drawn from urn II) 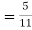
From(1), 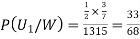
Example (2)Three urns contains 6 red, 4 black, 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. Lf the ball drawn is red find the probability that it is drawn from thefirst urn.
Solution:Let 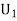 : the ball is drawn from urn 1.
: the ball is drawn from urn 1.
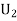 : the ball is drawn from urn lI.
: the ball is drawn from urn lI.
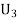 : the ball is drawn from urn 111.
: the ball is drawn from urn 111.
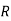 : the ball is red.
: the ball is red.
We have to find 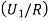 .
.
By Baye’s Theorem,
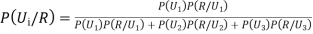 ... (1)
... (1)
Since the three urns are equally likely to be selected 
Also  (a red ball is drawn from urn
(a red ball is drawn from urn 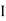 )
) 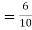
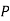 (R/
(R/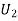 )
) 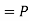 (a red ball is drawn from urn II)
(a red ball is drawn from urn II) 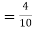
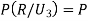 (a red ball is drawn from urn III)
(a red ball is drawn from urn III) 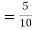
From (1), we have 
Example (3)ln a boltfactory machines 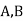 and
and 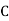 manufacturerespectively 25%, 35% and 40% of the total. Lf their output 5, 4 and 2 per cent are defective bolts. A bolt is drawn at random from theproduct and is found to be defective. What is the probability that it was manufactured by machine B.
manufacturerespectively 25%, 35% and 40% of the total. Lf their output 5, 4 and 2 per cent are defective bolts. A bolt is drawn at random from theproduct and is found to be defective. What is the probability that it was manufactured by machine B.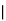 ?
?
Solution3: bolt is manufactured by machine 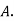
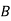 : bolt is manufactured by machine
: bolt is manufactured by machine 
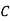 : bolt is manufactured by machine
: bolt is manufactured by machine 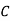
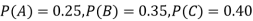
The probability ofdrawing a defective bolt manufactured by machine 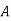 is
is  (D/A)
(D/A) 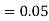
Similarly, 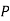 (D/B)
(D/B) 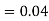 and
and 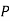 (D/C)
(D/C) 
By Baye’s theorem
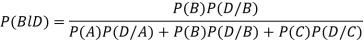
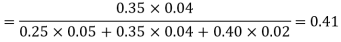
References
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010