UNIT 1
Periodic signals
Fourier series
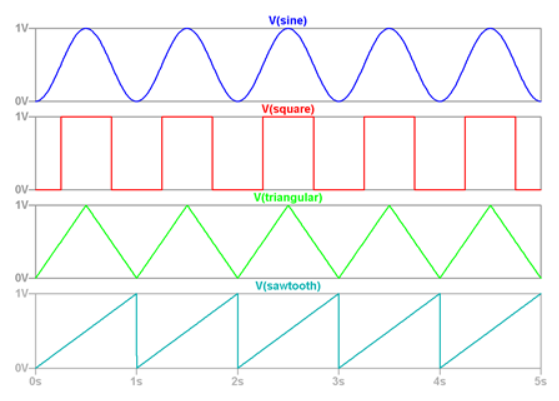
A function f(t) is said to be periodic if its image values are repeated at regular intervals in its domain. Thus the graph of a periodic function can be divided it ‘vertical strips’ that are replicas of each other, as illustrated in Figure 4.1. The interval between two successive replicas is called the period of the function. Therefore say that a function f(t) is periodic with period T if, for all its domain value f(t + mT) =f(t)
The term circular frequency, ω is also used in engineering, and is defined by: ω =circular frequency = 2π x frequency = 2π/T and is measured in radians per second. It is common to drop the term ‘circular’ and refer to this simply as the frequency when the context is clear. ‘Fourier’s theorem': This theorem states that a periodic function that satisfies certain conditions can be expressed as the sum of a number of sine functions of different amplitudes, phases and periods. That is, if f(t) is a periodic function with period T then
Fourier series of rectangular wave
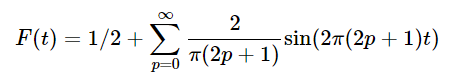
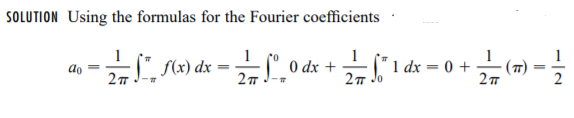
Fourier series of triangular wave
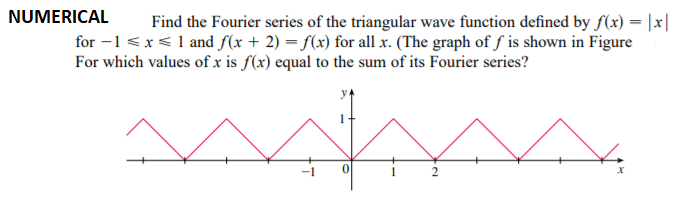
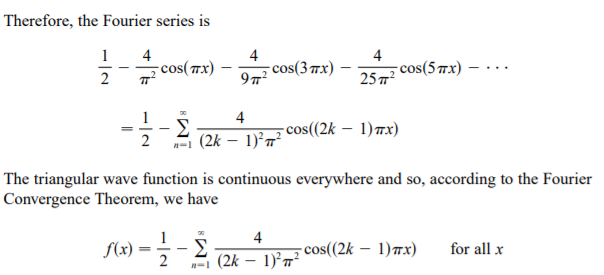
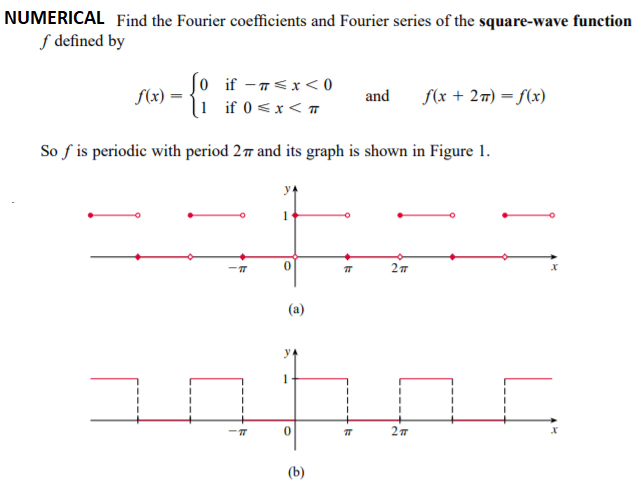
NUMERICAL:
Fourier series of sawtooth wave
![x(t)=\frac{a_0}{2}+\sum^\infty_{n=1} \left[a_n\cos\frac{2\pi nt}{T}+b_n\sin\frac{2\pi nt}{T}\right]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643239204_3221967.png)
Where
For the sawtooth function given,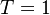 
, and 
is 0 therefore to reduce the equation to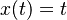 
.
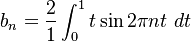
Let
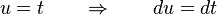
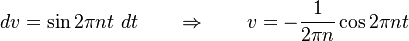
So
![b_n=2\left[t\left(-\frac{1}{2\pi n}\right)\cos 2\pi nt\bigg|_0^1+\frac{1}{2\pi n}\int_0^1\cos 2\pi nt\ dt \right]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643239204_762208.png)
![=2\left[\left(-\frac{1}{2\pi n}\cos 2\pi n - 0\right)+\left(\frac{1}{2\pi n}\right)^2\sin 2\pi nt \bigg|_0^1\right]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643239204_8295534.png)
![=2\left[-\frac{1}{2\pi n}(1)+0\right]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643239204_8760955.png)
Now, for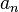 
consider 
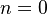separately.
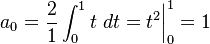
For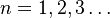 
, we have
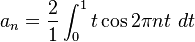
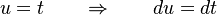
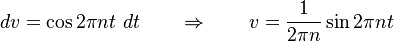
So
![a_n=2\left[t\left(\frac{1}{2\pi n}\right)\sin 2\pi nt\bigg|_0^1-\int_0^1\frac{1}{2\pi n}\sin 2\pi nt\ dt\right]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643239205_3470175.png)
![=2\left[\left(\frac{1}{2\pi n}\sin 2\pi n-0\right)-\left[-\left(\frac{1}{2\pi n}\right)^2\cos 2\pi nt\right]_0^1\right]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643239205_388418.png)
![=2\left[0+\left(\frac{1}{2\pi n}\right)^2\left(\cos 2\pi n-\cos 0\right)\right]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643239205_4556904.png)
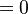
Therefore, the Fourier Transform representation of the sawtooth wave given is:
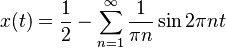
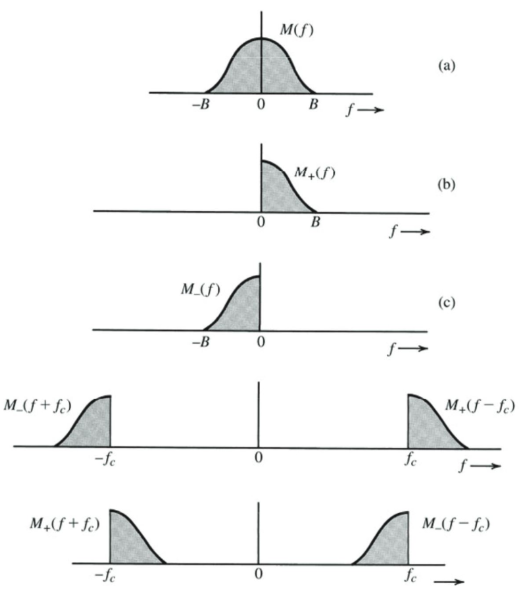
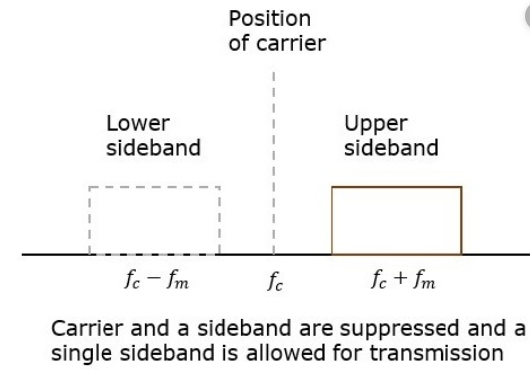
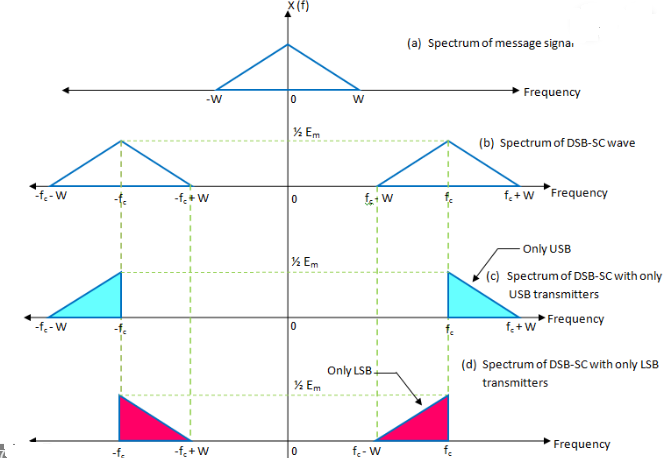
Single side band representation
References:
- Communication system by Bruce carison . TMH.
- Electronic Communication system by Kennedy IV Edition. TMH.
- Electronic Communication system by Roddey & Coolen, Pearson.
- Telecommunication system Engg. By Freeman John Wiley
- Communication system by Haykin,Wiley
