Module 2

Relational query languages

2.1 Relational algebra

Relational Algebra is procedural query language. It takes Relation as input and generates relation as output. Relational algebra mainly provides theoretical foundation for relational databases and SQL.

Basic Operations which can be performed using relational algebra are:

1. Projection
2. Selection
3. Join
4. Union
5. Difference
6. Intersection
7. Cartesian product
8. Division Operation

Consider following relation R (A, B, C)

Projection (π):

This operation is used to select particular columns from the relation.

Π(AB) R:

It will select A and B column from the relation R. It produces the output like:

Project operation automatically removes duplication from the resultant set.

Selection ():

This operation is used to select particular tuples from the relation.

 (C<4) R:

It will select the tuples which have value of c less than 4.

But select operation is used to only select the required tuples from the relation. To display those tuples on screen, select operation must be combined with project operation.

Π ( (C<4) R) will produce the result like:

2.2 Tuple and domain relational calculus

1. The tuple relational calculus is a nonprocedural language. The relational algebra was procedural.

We must provide a formal description of the information desired.

2.   A query in the tuple relational calculus is expressed as

i.e. the set of tuples  for which predicate 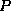 is true.

3.   We also use the notation

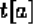 to indicate the value of tuple  on attribute .

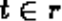 to show that tuple  is in relation .

Example Queries

1. For example, to find the branch-name, loan number, customer name and amount for loans over $1200:

This gives us all attributes, but suppose we only want the customer names. (We would use project in the algebra.)

We need to write an expression for a relation on scheme (cname).

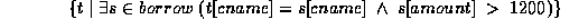
This query can be written as the set of all tuples  such that there exists a tuple  in the relation borrow for which the values of  and  for the cname attribute are equal, and the value of  for the amount attribute is greater than 1200.''

The notation 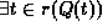 means there exists a tuple t in relation r such that predicate  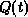is true''.

Consider more complex example.

Find all customers having a loan from the SFU branch, and the the cities in which they live: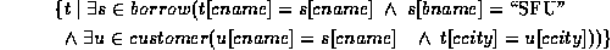

This query can be written as the set of all (cname,ccity) tuples for which cname is a borrower at the SFU branch, and ccity is the city of cname''.

Tuple variable ⸹ ensures that the customer is a borrower at the SFU branch.

Tuple variable u  is restricted to pertain to the same customer as , and also ensures that ccity is the city of the customer.

The logical connectives 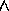 (AND) and  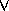(OR) are allowed, as well as  (negation).

We also use the existential quantifier  and the universal quantifier .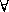

Some more examples:

1. Find all customers having a loan, an account, or both at the SFU branch:

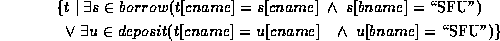
2. Find customers who have an account, but not a loan at the SFU branch.

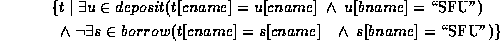
3. Find all customers who have an account at all branches located in Brooklyn. (We used division in relational algebra.)

For this example we will use implication, denoted by a pointing finger in the text, but by 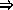 here.

The formula 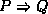 means 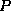 implies , or, if 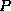 is true, then  must be true.

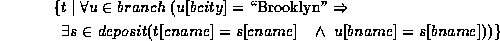
This query can be written as:  the set of all cname tuples  such that for all tuples  in the branch relation, if the value of  on attribute bcity is Brooklyn, then the customer has an account at the branch whose name appears in the bname attribute of .

2.3 SQL3, DDL and DML constructs

In a relational database, view in nothing but Virtual Table. It is computed at run time from the data in the database when access to view is requested.  It is a result set of a stored query on the data. The query command of view is kept in database dictionary.   

Unlike ordinary base tables in a relational database, a view does not form part of the physical schema. Changes applied to the data in a relevant underlying table are reflected in the data shown in subsequent invocations of the view.

Advantages of Views over relational tables:

• Views represent a subset of the data contained in a table on which it is defined. A given user may have permission to query the view, while denied access to the rest of the base table.
• Views can join multiple tables into a single virtual table.
• Views can act as aggregated tables, where the database engine aggregates data (sum, average, etc.) and presents the calculated results as part of the data.
• Unlike relational table, views take very little space to store. The database does not contain copy of data but just the definition of a view.
• Depending on the SQL engine used, views can provide extra security.

SQL and View Equivalence

A view is equivalent to its source query. When queries are run against views, the query is modified.

For example, if there exists a view named CUST_ACCT with the content as follows:

CREATE VIEW CUST_ACCT AS SELECT A.CUST_ID,A.CUST_NAME,A.ACCT_ID,

B.BALANCE FROM CUST A JOIN ACCOUNT B

ON A.ACCT_ID=B.ACCT_ID;

Above query creates view CUST_ACCT.

2.4 Relational database design: Domain and data dependency

Domain variables take on values from an attribute's domain, rather than values for an entire tuple.

Formal Definitions

1. An expression is of the form

Where the 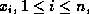 represent domain variables, and  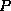is a formula.

2.     An atom in the domain relational calculus is of the following forms

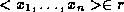•  where  is a relation on  attributes, and , are domain variables or constants.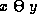
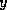• , where  and  are domain variables, and  is a comparison operator.
• , where c is a constant.

1. Formulae are built up from atoms using the following rules:
   • An atom is a formula.
   • If 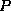 is a formula, then so are  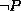and .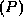
   • If 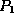 and 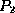 are formulae, then so are 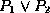,  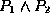and .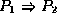
   • If 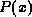 is a formula where x is a domain variable, then so are  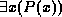and .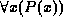

Example Queries

1. Find branch name, loan number, customer name and amount for loans of over $1200.

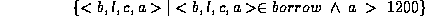
2.     Find all customers who have a loan for an amount > than $1200.

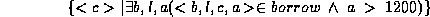
3.     Find all customers having a loan from the SFU branch, and the city in which they live.

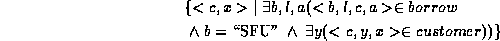
4.     Find all customers having a loan, an account or both at the SFU branch.

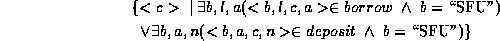
5.     Find all customers who have an account at all branches located in Brooklyn.

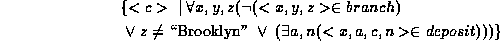
6.     If you find this example difficult to understand, try rewriting this expression using implication, as in the tuple relational calculus example. Here's my attempt:

2.5 Normal forms

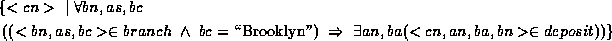
Normalization is often executed as a series of different forms. Each normal form has its own proerties. As normalization proceeds, the relations become progressively more restricted in format, and also less vulnerable to update anomalies. For the relational data model, it is important to bring the realtion only in first normal form (1NF) that is critical in creating relations. All the remaining forms are optional.A relation R is said to be normalized if it does not create any anomaly for three basic operations: insert, delete and update.

Different form of normalization:

Fig.2.3 Normalization Forms

First Normal Form (1NF):

A relation r is in 1NF if and only if every tuple contains only atomic attributes means exactly one value for each attribute. As per the rule of first normal form, an attribute of a table cannot hold multiple values. It should hold only atomic values.

Example: suppose Company has created a employee table to store name, address and mobile number of employees.

In above table, two employees John, Mary has two mobile numbers. So the attribute, emp_mobile is Multivalued attribute.

So this table is not in 1NF as the rule says, “Each attribute of a table must have atomic values”. But in above table the the attribute, emp_mobile, is not atomic attribute as it contains multiple values. So it violates the rule of 1 NF.

Following solution brings employee table in 1NF.

Second Normal Form (2NF)

A table is said to be in 2NF if both of the following conditions are satisfied:

      Table is in 1 NF.

      No non-prime attribute is dependent on the proper subset of any candidate key of table. It means non-prime attribute should fully functionally dependant on whole candidate key of a table. It should not depend on part of key.

An attribute that is not part of any candidate key is known as non-prime attribute.

Example: Suppose a school wants to store data of teachers and the subjects they teach. Since a teacher can teach more than one subjects, the table can have multiple rows for the same teacher.

For above table:

Candidate Keys: {Teacher_Id, Subject}
Non prime attribute: Teacher_Age

The table is in 1 NF because each attribute has atomic values. However, it is not in 2NF because non prime attribute Teacher_Age is dependent on Teacher_Id alone which is a proper subset of candidate key. This violates the rule for 2NF as the rule says “no non-prime attribute is dependent on the proper subset of any candidate key of the table”.

To bring above table in 2NF we can break it in two tables (Teacher_Detalis and Teacher_Subject) like this:

Teacher_Details table:

Teacher_Subject table:

Now these two tables are in 2NF.

Third Normal Form (3NF)

A table design is said to be in 3NF if both the following conditions hold:

• Table must be in 2NF.
• Transitive functional dependency from the relation must be removed.

So it can be stated that, a table is in 3NF if it is in 2NF and for each functional dependency P->Q at least one of the following conditions hold:

• P is a super key of table
• Q is a prime attribute of table

An attribute that is a part of one of the candidate keys is known as prime attribute.

2.6 Dependency preservation

Functional dependency describes the relationship between attributes in a relation.For example, if A and B are attributes of relation R, and B is functionally dependent on A ( denoted A --> B), if each value of A is associated with exactly one value of B. ( A and B may each consist of one or more attributes.)

Fig.2.2 Functional Dependency

In Emp_dept relation: -  Ssn is P.K. So, it determines Ename, bdate, address and Dno.

Example:-

F.D.S in above relation:-

Example:-

A -> C , A -> D,  AB -> C,  AC -> D,  ABC -> D, C -> A, D -> A, AB -> d, BC -> D             

Closure:-

The set of all dependencies that include F as well as all dependencies that can be derived from F is called the closure of F and is denoted by F+.

F for Emp_Dept is:-

F={Ssn -> {Ename, Bdate, Address, Dno}, Dno -> {Dname, Dmgr_Ssn}}

In addition to these, some dependencies can be inferred from F:-

Ssp -> Dname, Dmgr_Ssn

Ssn -> Ssn

Dno -> Dname

We must discover a set of inference rules that can be used to infer new dependencies from a given set of dependencies.

2.7 Lossless design

It means after decomposition, if we will try to join decomposed relations, we should get original relation without loss of any information

2.8 Query processing and optimization: Evaluation of relational algebra expressions

Consider the relational database given below:

Employee (emp_name,street,city)

Works(emp_name, company_name,salary)

Company(company_name, city)

Manager(emp_name, manager_name)

Write a query for each of the following :

1. Find the emp_name, street and cities of residence of employees whose salary exists in between 10000 and 20000 and work for ABC Ltd.
2. Find the name, street and cities of employees who live in the same city as the company they work for.
3. Find all employees in the database who earn more than each employee of Central Bank.
4. Find the company that has the most employees.
5. Find the company that has the smallest salary payout.
6. Find those companies whose employees earn a higher salary, on average, than the average salary at Central Bank.
7. Find all employees who live in the same city and on the same street as do the manager.
8. Find the names of employee who do not work for ABC Ltd. 

SOLUTION:

1 . Find the emp_name, street and cities of residence of employees whose salary exists in between 10000 and 20000 and work for ABC Ltd.

SELECT emp_name,street,city FROM employee WHERE emp_name IN (SELECT emp_name FROM works WHERE company_name = ‘ABC Ltd’ AND (salary BETWEEN 10000 AND 20000));

2.Find the name, street and cities of employees who live in the same city as the company they work for.

SELECT A.name,A.street,A.cities FROM employees as A, works as B, company as C WHERE A.emp_name=B.emp_name AND B.company_name=C.company_name AND A.city = C.city;

3. Find all employees in the database who earn more than each employee of Central Bank.

SELECT emp_name FROM works WHERE salary>ALL(SELECT salary FROM works WHERE company_name = ‘Central Bank’);

4. Find the company that has the most employees.

SELECT company_name FROM works GROUP BY company_name HAVING COUNT (DISTINCT emp_name) >= ALL (SELECT COUNT(DISTINCT emp_name FROM works GROUP BY company_name);

5. Find the company that has the smallest salary payout.

SELECT company_name FROM works GROUP BY  company_name HAVING SUM (salary) <= ALL (SELECT SUM (salary) FROM works GROUP BY company_name);

6. Find those companies whose employees earn a higher salary, on average, than the average salary at Central Bank.

SELECT company_name FROM works GROUP BY  company_name HAVING AVG(salary) > (SELECT AVG (salary) FROM works WHERE compnay_name =‘Central Bank’);

7. Find all employees who live in the same city and on the same street as do the manager.

SELECT A.name,A.street,A.city FROM employees as A.manages as B, employee as C WHERE A.emp_name = B.emp_name AND B.manager_name = C.emp_name AND A.street = C.stree AND A.city=C.city;

8. Find the names of employee who do not work for ABC Ltd.

SELECT emp_name FROM works WHERE company_name <> ‘ABC Ltd.’;

2.9 Query equivalence

Query processing in nothing but steps involved in retrieving data from database. These activities include translation of queries written high level database language into expressions that can be understood at the physical level of the file system. It also includes a variety of query optimizing transformations and actual evaluations of queries.

Query Processing Procedure:

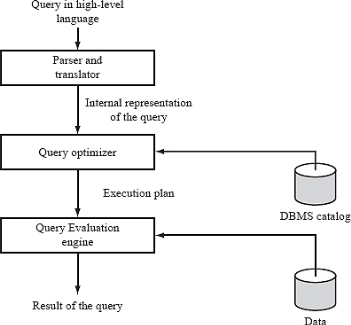
Fig. Query Processing Steps

Basic steps in query processing are:

1. Parsing and translation
2. Optimization
3. Evaluation

At the beginning of query processing, the queries must be translated into a form which could be understood at the physical level of the system. A language like SQL is not suitable for the internal representation of a query. Relational algebra is the good option for internal representation of query.

So, the first step in query processing is to translate a given query into its internal representation. In generating internal form of a query, parser checks the syntax of the query written by user, verifies that the relation names appearing in the query really exists in the database and so on.

The system constructs a parse-tree of the query. Then this tree is translated into relational-algebra expressions. If the query was expressed in terms of a view, the translation phase replaces all uses of the view by the relational-algebra expression that defines the view.

One query can be answered in different ways. Relational-algebra representation of a query specifies only partially how to evaluate a query. There are different ways to evaluate relational-algebra expressions. Consider the query:

Select acc_balance from account where acc_balance<5000

This query can be translated into one of the following relational-algebra expressions:

1. acc_balance<5000 (Πacc_balance (account))

2.        Πacc_balance (acc_balance<5000 (account))

Different algorithms are available to execute relational-algebra operation. To solve the above query, we can search every tuple in account to find the tuples having balance less than 5000. If a B+ tree index is available on the balance attribute, we can use this index instead to search for the required tuples.

To specify how to evaluate a query, we need not only to provide the relational-algebra expression, but also to explain it with instructions specifying the procedure for evaluation of each operation.

Account Relation

Customer Relation

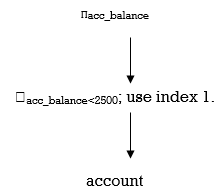
Fig Query-Evaluation Plan

A relational-algebra operation along with instructions on how to evaluate it is called an evaluation primitive. A sequence of primitive operations that can be used in the evaluation of a query is called a query execution plan or query evaluation plan. Above figure illustrates an evaluation plan for our example query, in which a particular index is specified for the selection operation from database. The query execution engine takes a query evaluation plan, executes that plan, and returns the answer to the query.

Different evaluation plans have different costs. It is the responsibility of the system to construct a query evaluation plan that minimizes the cost of query evaluation; this task is called Query Optimization. Once the query plan with minimum cost is chosen, the query is evaluated with the plan, and the result of the query is the output.  In order to optimize a query, a query optimizer must know the cost of each operation.

Although the exact cost is hard to compute, it is possible to get a rough estimate of execution cost for each operation. Exact cost is hard for computation because it depends on many parameters such as actual memory available to execute the operation.

Catalog Information for Cost Estimation

Information about relations and attributes:

• NR: number of tuples in the relation R.

• BR: number of blocks that contain tuples of the relation R.

• SR: size of a tuple of R.

• FR: blocking factor; number of tuples from R that fit into one block (FR = dNR/BRe)

• V(A, R): number of distinct values for attribute A in R.

• SC(A, R): selectivity of attribute A ≡ average number of tuples of R that satisfy an equality condition on A.

SC(A, R) = NR/V(A, R).

Information about indexes:

• HTI: number of levels in index I (B+-tree).

• LBI: number of blocks occupied by leaf nodes in index I (first-level blocks).

• ValI: number of distinct values for the search key.

Measures of Query Cost:

The cost of query evaluation can be measured in terms of number of different resources used, including disk accesses, CPU time to execute given query, and, in a distributed database or parallel database system. In large database systems, however, the cost to access data from disk is usually the most important cost, since disk accesses are slow compared to in-memory operations. Moreover, CPU speeds have been improving much faster than have disk speeds. The CPU time taken for a task is harder to estimate since it depends on low-level details of the execution.

The time taken by CPU is negligible in most systems when compared with the number of disk accesses.

If we consider the number of block transfers as the main component in calculating the cost of a query, it would include more sub-components. Those are as below:

Rotational latency – time taken to bring and turn the required data under the read-write head of the disk.

Seek time – It is the time taken to position the read-write head over the required track or cylinder.

Sequential I/O – reading data that are stored in contiguous blocks of the disk

Random I/O – reading data that are stored in different blocks of the disk that are not contiguous.

From these sub-components, we would list the components of a more accurate measure as follows;

• The number of seek operations performed
• The number of block read operations performed
• The number of blocks written operations performed

Hence, the total query cost can be written as follows;

2.10 Join strategies

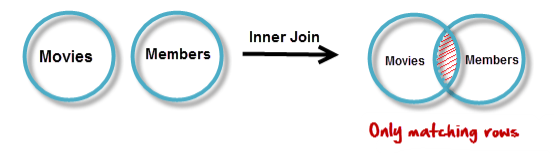
INNER JOIN

The inner JOIN is used to return rows from both tables that satisfy the given condition.

Suppose , you want to get list of members who have rented movies together with titles of movies rented by them. You can simply use an INNER JOIN for that, which returns rows from both tables that satisfy with given conditions.

SELECT A.first_name , A.last_name , B.title

FROM membersAS A

INNER JOIN movies AS B

ON B.id = A.movie_id

OUTER JOIN

MySQL Outer JOINs return all records matching from both tables .

It can detect records having no match in joined table. It returns NULL values for records of joined table if no match is found.

LEFT OUTER JOIN

Assume now you want to get titles of all movies together with names of members who have rented them. It is clear that some movies have not being rented by any one. We can simply use LEFT JOIN for the purpose.

SELECT A.title , B.first_name , B.last_name

FROM movies AS A

LEFT JOIN members AS B

ON B.movie_id = A.id

The LEFT JOIN returns all the rows from the table on the left even if no matching rows have been found in the table on the right. Where no matches have been found in the table on the right, NULL is returned.

RIGHT OUTER JOIN

RIGHT JOIN is obviously the opposite of LEFT JOIN. The RIGHT JOIN returns all the columns from the table on the right even if no matching rows have been found in the table on the left. Where no matches have been found in the table on the left, NULL is returned.

In our example,  let's assume that you need to get names of members and movies rented by them. Now we have a new member who has not rented any movie yet

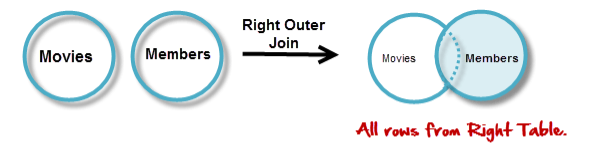
SELECT  A.first_name , A.last_name, B.title

FROM members AS A

RIGHT JOIN movies AS B

ON B.id = A.movie_id

2.11 Query optimization algorithms

•  First, it provides the user with faster results, which makes the application seem faster to the user.
• Secondly, it allows the system to service more queries in the same amount of time, because each request takes less time than un-optimized queries.
• Thirdly, query optimization ultimately reduces the amount of wear on the hardware (e.g. Disk drives), and allows the server to run more efficiently (e.g. Lower power consumption, less memory usage).

References:

1. “Principles of Database and Knowledge – Base Systems”, Vol 1 by J. D. Ullman, Computer Science Press.

2. “Fundamentals of Database Systems”, 5th Edition by R. Elmasri and S. Navathe, Pearson Education

3. “Foundations of Databases”, Reprint by Serge Abiteboul, Richard Hull, Victor Vianu, Addison-Wesley