Module 1
Introduction
Definition − An alphabet is any finite set of symbols.
Example − ∑ = {a, b, c, d} is an alphabet set where ‘a’, ‘b’, ‘c’, and ‘d’ are symbols.
Definition − A language is a subset of ∑* for some alphabet ∑. It can be finite or infinite.
Example − If the language takes all possible strings of length 2 over ∑ = {a, b}, then L = { ab, aa, ba, bb }
Grammar
Simplifying Context Free Grammars
A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production rules satisfy one of the following conditions:
● A non-terminal generating a terminal (e.g.; X->x)
● A non-terminal generating two non-terminals (e.g.; X->YZ)
● Start symbol generating ε. (e.g.; S->ε)
Consider the following grammars,
G1 = {S->a, S->AZ, A->a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
Note –
● CNF is a pre-processing step used in various algorithms.
● For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.
How to convert CFG to CNF?
Step 1. Remove start from RHS. If start symbol S is at the RHS of any production in the grammar, create a new production as:S0->S where S0 is the new start symbol.
Step 2. Remove null, unit and useless productions. If CFG comprises of any production rules, remove them.
Step 3. Remove terminals from RHS. For eg; production rule X->xY can be decomposed as: X->ZY Z->x
Step 4. Remove RHS with more than two non-terminals. e.g,; production rule X->XYZ can be decomposed as:
X->PZ
P->XY
A production, if it's left side occurs on its right side, is called recursive. Production S→aS, for example, is recursive. A manufacturing A → α is recursive indirectly. If a sentence form that includes A is derived from A, then suppose we have the following grammar :
S → b/aA
A → c/bS
Due to the following derivations, the S → aA and A→ bs productions are both indirectly recursive:
S ⇒ aA ⇒ abS,
A ⇒ bS ⇒ baA
A grammar is recursive if either a recursive or indirectly recursive production is included in it.
Derivation
Derivation is a sequence of the laws of development. Via these production laws, it is used to get the input string. We have to make two decisions during parsing. That are like the following:
● The non-terminal that is to be replaced must be determined by us.
● We have to determine the law of development by which the non-terminal would be substituted.
We have two options to assess which non-terminal with the production rule is to be put.
The input is scanned and replaced with the development rule from left to right in the left-most derivation. So, we read the input string from left to right in the left-most derivation.
2. Right most derivation
The input is scanned and replaced with the production rule from right to left in the right-most derivation. So, we read the input string from right to left in the right - most derivation.
The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows :
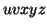
Fig 1: Chomsky hierarchy
The above diagram shows the hierarchy of chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.
● Type 0 grammar -
Type 0 grammar is known as Unrestricted grammar.The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.
Example :
● Type 1 grammar -
Type 1 grammar is known as Context Sensitive Grammar.Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:
● There may be more than one symbol on the left side of their development rules for context-sensitive grammar.
● The number of left-hand symbols does not surpass the number of right-hand symbols.
● The A → ε type rule is not permitted unless A is a beginning symbol. It does not occur on the right-hand side of any rule.
● The Type 1 grammar should be Type 0. Production is in the form of V →T in type1
Key takeaway :
● Where the number of symbols in V is equal to or less than T
Example :
● Type 2 grammar -
Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is :
A → α
Key takeaway :
● Where A is any single non-terminal and is any combination of terminals and non-terminals.
Example :
● Type 3 grammar -
Type 3 Grammar is called Regular Grammar.Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modelled.
Type3 has to be in the form of -
V → T*V / T*
Example :
A → xy
Key takeaway :
● The most limited form of grammar is Type3. Type2 and Type1 should be the grammar of Type3.
A Regular Expression can be recursively defined as follows −
● ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
● φ is a Regular Expression denoting an empty language. (L (φ) = { })
● x is a Regular Expression where L = {x}
● If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then
● If we apply any of the rules several times from 1 to 5, they are Regular Expressions.
Unix Operator Extensions
Regular expressions are used frequently in Unix:
● In the command line
● Within text editors
● In the context of pattern matching programs such as grep and egrep
Additional operators are recognized by unix. These operators are used for convenience only.
● character classes: '[' <list of chars> ']'
● start of a line: '^'
● end of a line: '$'
● wildcard matching any character except newline: '.'
● optional instance: R? = epsilon | R
● one or more instances: R+ == RR*
In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.
An automaton can be represented by a 5-tuple (Q, ∑, δ, q0, F), where −
● Q is a finite set of states.
● ∑ is a finite set of symbols, called the alphabet of the automaton.
● δ is the transition function.
● q0 is the initial state from where any input is processed (q0 ∈ Q).
● F is a set of final state/states of Q (F ⊆ Q).
A Review (supplemental)
Recall the example of designing a vending machine selling 20-dolllar food packs in Figure 1.3.2.What abstract concepts are involved in the design? ⇒ See the definition next.
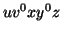
Figure Recall the example
Advantages and disadvantages
● DFAs were invented to model of a Turing machine, which was too general to study properties of real world machines.
● DFAs are one of the most practical models of computation, since there is a trivial linear time, constant-space, online algorithm there are efficient algorithms to find a DFA recognizing:
● The union/intersection of the languages recognized by two given DFAs.
● The complement of the language recognized by a given DFA.
● On the other hand, finite state automata are of strictly limited power in the languages they can recognize; many simple languages, including any problem that requires more than constant space to solve, cannot be recognized by a DFA. • The classical example of a simply described language that no DFA can recognize is bracket language, i.e., language that consists of properly paired brackets such as word "(( )( ))".
In NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine. In other words, the exact state to which the machine moves cannot be determined. Hence, it is called Non-deterministic Automaton. As it has finite number of states, the machine is called Non-deterministic Finite Machine or Non-
deterministic Finite Automaton.
Q → Finite non-empty set of states.
∑ → Finite non-empty set of input symbols.
∂ → Transitional Function.
q0 → Beginning state.
F → Final State
● Review of a previous example of DFA
● Original version --- see Fig. (the same as Fig.)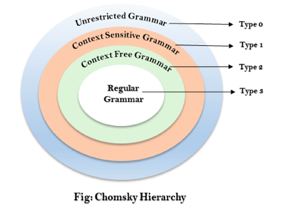
Figure Step 1 For NDFA Example
A nondeterministic finite automaton (NFA) version of the above DFA --- see Fig. 2.
● More intuitive!
● How to design an NFA will be described later.
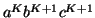
Figure Step 1 For NDFA Example
Some properties of NFA’s (see Fig. 2.6 for the illustration) ---
Some transitions may “die,” like ˆ δ (q2, 0).
Some transitions have multiple choices, like ˆ δ (q0, 0) = q0 and q2.
Example --- Design an NFA accepting the following language L = {w | w∈{0, 1}* and ends in 01}.
DFA vs NDFA
The following table lists the differences between DFA and NDFA.
DFA | NDFA |
The transition from a state is to a single particular next state for each input symbol. Hence it is called deterministic. | The transition from a state can be to multiple next states for each input symbol. Hence it is called non-deterministic. |
Empty string transitions are not seen in DFA. | NDFA permits empty string transitions. |
Backtracking is allowed in DFA | In NDFA, backtracking is not always possible. |
Requires more space. | Requires less space. |
A string is accepted by a DFA, if it transits to a final state. | A string is accepted by a NDFA, if at least one of all possible transitions ends in a final state. |
Regular expressions and finite automata have equivalent expressive power:
● For every regular expression R, there is a corresponding FA that accepts the set of strings generated by R.
● For every FA A there is a corresponding regular expression that generates the set of strings accepted by A.
The proof is in two parts:
Our construction of FA from regular expressions will allow "epsilon transitions" (a transition from one state to another with epsilon as the label). Such a transition is always possible, since epsilon (or the empty string) can be said to exist between any two input symbols. We can show that such epsilon transitions are a notational convenience; for every FA with epsilon transitions there is a corresponding FA without them.
Constructing an FA from an RE
We begin by showing how to construct an FA for the operands in a regular expression.
● If the operand is a character c, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and a transition from s0 to sF with label c.
● If the operand is epsilon, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and an epsilon transition from s0 to sF.
● If the operand is null, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and no transitions.
Given FA for R1 and R2, we now show how to build an FA for R1R2, R1|R2, and R1*. Let A (with start state a0 and final state aF) be the machine accepting L(R1) and B (with start state b0 and final state bF) be the machine accepting L(R2).
● The machine C accepting L(R1R2) includes A and B, with start state a0, final state bF, and an epsilon transition from aF to b0.
● The machine C accepting L(R1|R2) includes A and B, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and b0, and from aF and bF to cF.
● The machine C accepting L(R1*) includes A, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and cF, and from aF to a0, and from aF to cF.
Eliminating Epsilon Transitions
If epsilon transitions can be eliminated from an FA, then construction of an FA from a regular expression can be completed.
Epsilon transitions offers a choice: It allows us to stay in a state or move to a new state, regardless of the input symbol.
If starting in state s1, state s2 can be reached via a series of epsilon transitions followed by a transition on input symbol x, replacement of the epsilon transitions with a single transition from s1 to s2 on symbol x.
Algorithm for Eliminating Epsilon Transitions
A finite automaton F2 can be build with no epsilon transitions from a finite automaton F1 as follows:
For each pair of states i and j in F2, there is a transition from state i to state j on input x if there exists a state k that is reachable from state i via epsilon transitions in F1, and there is a transition in F1 from state k to state j on input x.
Regular languages are closed under a wide variety of operations.
Union and intersection
Pick DFAs recognizing the two languages and use the cross-product construction to build a DFA recognizing their union or intersection. See Sipser Theorem 1.25. Also see Sipser 1.45 for another way to do union.
Set complement
Pick a DFA recognizing the language, then swap the accept/non-accept markings on its states.
String reversal
Pick an NFA recognizing the language. Create a new final state, with epsilon transitions to it from all the old final states. Then swap the final and start states and reverse all the transition arrows.
Set difference
Re-write set difference using a combination of intersection and set complement
Concatenation and Star
Pick an NFA recognizing the language and modify it as described in Sipser Theorems 1.47 and 1.49
Homomorphism
A homomorphism is a function from strings to strings. What makes it a homomorphism is that its output on a multi-character string is just the concatenation of its outputs on each individual character in the string. Or, equivalently, h(xy) = h(x)h(y) for any strings x and y. If S is a set of strings, then h(S) is {w : w = h(x) for some x in S}.
To show that regular languages are closed under homomorphism, choose an arbitrary regular language L and a homomorphism h. It can be represented using a regular expression R. But then h(R) is a regular expression representing h(L). So h(L) must also be regular.
Notice that regular languages are not closed under the subset/superset relation. For example, 0*1* is regular, but its subset {On1n : n >= 0} is not regular, but its subset {01, 0011, 000111} is regular again.
Lemma: The language 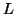 =
= 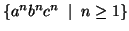 is not context free.
is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let 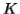 be the constant of the Pumping Lemma.
be the constant of the Pumping Lemma.
Considering the string 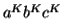 , where
, where 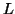 is length greater than
is length greater than 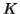 .
.
By the Pumping Lemma this is represented as 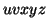 , such that all
, such that all 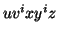 are also in
are also in 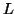 , which is not possible, as:
, which is not possible, as:
either 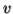 or
or 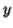 cannot contain many letters from
cannot contain many letters from 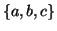 ; else they are in the wrong order .
; else they are in the wrong order .
if 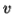 or
or 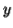 consists of a's, b's or c's, then
consists of a's, b's or c's, then 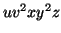 cannot maintain the balance amongst the three letters.
cannot maintain the balance amongst the three letters.
Lemma: The language 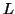 =
= 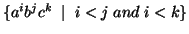 is not context free.
is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let 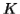 be the constant of the Pumping Lemma.
be the constant of the Pumping Lemma.
Considering the string 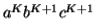 , which is
, which is 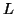 >
> 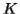 .
.
By the Pumping Lemma this must be represented as 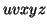 , such that all
, such that all 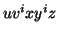 are also in
are also in 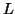 .
.
-As mentioned previously neither 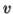 nor
nor 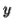 may contain a mixture of symbols.
may contain a mixture of symbols.
-Suppose 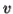 consists of a's.
consists of a's.
Then there is no way 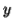 cannot have b's and c's. It generate enough letters to keep them more than that of the a's (it can do it for one or the other of them, not both).
cannot have b's and c's. It generate enough letters to keep them more than that of the a's (it can do it for one or the other of them, not both).
Similarly 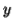 cannot consist of just a's.
cannot consist of just a's.
-So suppose then that 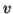 or
or 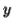 contains only b's or only c's.
contains only b's or only c's.
Consider the string 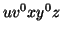 which must be in
which must be in 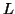 . Since we have dropped both
. Since we have dropped both 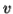 and
and 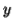 , we must have at least one b' or one c' less than we had in
, we must have at least one b' or one c' less than we had in 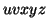 , which was
, which was 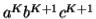 . Consequently, this string no longer has enough of either b's or c's to be a member of
. Consequently, this string no longer has enough of either b's or c's to be a member of 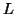 .
.
1. Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.
2. Dexter C. Kozen, Automata and Computability, Undergraduate Texts in Computer Science, Springer.
3. Michael Sipser, Introduction to the Theory of Computation, PWS Publishing.
4. John Martin, Introduction to Languages and the Theory of Computation, Tata McGraw Hill.