2.1 Contextfree grammars CFG and Contextfree languages CFL | unit 2 context free languages and pushdown automata

FLAT

Module 2

Context-free languages and pushdown automata:

2.1 Context-free grammars (CFG) and Context-free languages (CFL)

CFLs are used by the compiler in the parsing phase as they define the syntax of a programming language and are used in many editors.

There are four important components in a grammatical description of a language:

There is a set of symbols that form the strings of the language being defined. They are called terminal symbols, represented by Vt.

There is a finite set of variables, called non-terminals. These are represented by Vn.

One of the variable represents the language being defined; it is called the start symbol. It is represent by S.

There are finite set of rules called productions that represent the recursive definition of a language. Each production consists of:

A variable that is being defined by the production. This variable is often called the head of the production.
The production symbol ->.
A string of zero or more terminals and variable.

Formal definition

A context-free grammar (CFG) is a 4-tuple G=(Vn, Vt, S, P), where Vn and Vt are disjoint finite sets, S is an element of Vn, and P is a finite set of formulas of the form A -> α, where A ϵ Vn and α ϵ (Vn U Vt)*.

2.2 Chomsky and Greibach normal forms

Chomsky normal forms

A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production rules satisfy one of the following conditions:

A non-terminal generating a terminal (e.g.; X->x)

A non-terminal generating two non-terminals (e.g.; X->YZ)

Start symbol generating ε. (e.g.; S->ε)

Consider the following grammars,

G1 = {S->a, S->AZ, A->a, Z->z}

G2 = {S->a, S->aZ, Z->a}

The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.

Note –

CNF is a pre processing step used in various algorithms.

For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.

Greibach normal forms

A CFG is in Greibach Normal Form if the Productions are in the following forms −

A → b

A → bD1…Dn

S → ε

where A, D1,....,Dn are non-terminals and b is a terminal.

Algorithm to Convert a CFG into Greibach Normal Form

Step 1 − If the start symbol S occurs on some right side, create a new start symbol S’ and a new production S’ → S.

Step 2 − Remove Null productions. (Using the Null production removal algorithm discussed earlier)

Step 3 − Remove unit productions. (Using the Unit production removal algorithm discussed earlier)

Step 4 − Remove all direct and indirect left-recursion.

Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.

Problem

Convert the following CFG into CNF

S → XY | Xn | p

X → mX | m

Y → Xn | o

Solution

Here, S does not appear on the right side of any production and there are no unit or null productions in the production rule set. So, we can skip Step 1 to Step 3.

Step 4

Now after replacing

X in S → XY | Xo | p

with

mX | m

we obtain

S → mXY | mY | mXo | mo | p.

And after replacing

X in Y → Xn | o

with the right side of

X → mX | m

we obtain

Y → mXn | mn | o.

Two new productions O → o and P → p are added to the production set and then we came to the final GNF as the following −

S → mXY | mY | mXC | mC | p

X → mX | m

Y → mXD | mD | o

O → o

P → p

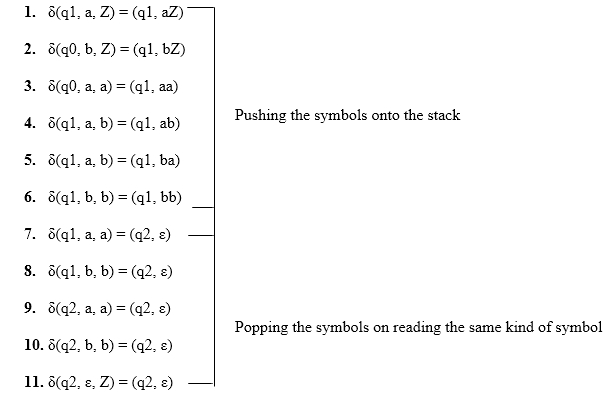
2.3 Non deterministic pushdown automata (PDA) and equivalence with CFG

The non-deterministic pushdown automata is very much similar to NFA. We will discuss some CFGs which accepts NPDA.

The CFG which accepts deterministic PDA accepts non-deterministic PDAs as well. Similarly, there are some CFGs which can be accepted only by NPDA and not by DPDA. Thus NPDA is more powerful than DPDA.

Example:

Design PDA for Palindrome strips.

Solution:

Suppose the language consists of string L = {aba, aa, bb, bab, bbabb, aabaa, ......]. The string can be odd palindrome or even palindrome. The logic for constructing PDA is that we will push a symbol onto the stack till half of the string then we will read each symbol and then perform the pop operation. We will compare to see whether the symbol which is popped is similar to the symbol which is read. Whether we reach to end of the input, we expect the stack to be empty.

This PDA is a non-deterministic PDA because finding the mid for the given string and reading the string from left and matching it with from right (reverse) direction leads to non-deterministic moves. Here is the ID.

Non-deterministic Pushdown Automata

Simulation of abaaba

δ(q1, abaaba, Z) Apply rule 1

⊢ δ(q1, baaba, aZ) Apply rule 5

⊢ δ(q1, aaba, baZ) Apply rule 4

⊢ δ(q1, aba, abaZ) Apply rule 7

⊢ δ(q2, ba, baZ) Apply rule 8

⊢ δ(q2, a, aZ) Apply rule 7

⊢ δ(q2, ε, Z) Apply rule 11

⊢ δ(q2, ε) Accept

2.4 Parse trees

Derivation Tree

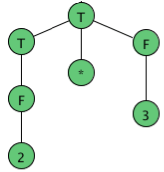
Figure Parse trees

A parse tree is an entity which represents the structure of the derivation of a terminal string from some non-terminal. Key features to define are the root ∈ V and yield ∈ Σ* of each tree.

For each σ ∈ Σ, there is a tree with root σ and no children; its yield is σ

For each rule A → ε, there is a tree with root A and one child ε; its yield is ε

If t1, t2, ..., tn are parse trees with roots r1, r2, ..., rn and respective yields y1, y2, ..., yn, and A → r1r2...rn is a production, then there is a parse tree with root A whose children are t1, t2, ..., tn. Its root is A and its yield is the concatenation of yields: y1y2...yn

Here, parse trees are constructed from bottom up, not top down.

The actual construction of "adding children" should be made more precise, but we intuitively know what's going on.

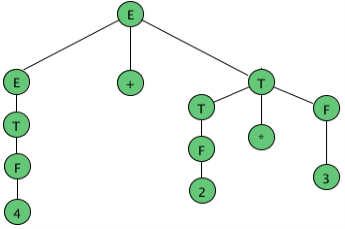
As an example, here are all the parse (sub) trees used to build the parse tree for the arithmetic expression 4 + 2 * 3 using the expression grammar

E → E + T | E - T | T

T → T * F | F

F → a | ( E )

where a represents an operand of some type, be it a number or variable. The trees are grouped by height.

Figure Example of Parse trees

Parse Trees and Derivations

A derivation is a sequence of strings in V* which starts with a non-terminal in V-Σ and ends with a string in Σ*.

Let's consider the sample grammar

E → E+E | a

We write:

E ⇒ E+E ⇒ E+E+E ⇒a+E+E⇒a+a+E⇒a+a+a

but this is incomplete, because it doesn't tell us where the replacement rules are applied.

We actually need "marked" strings which indicate which non-terminal is replaced in all but the first and last step:

E ⇒ Ě+E ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a

In this case, the marking is only necessary in the second step; however it is crucial, because we want to distinguish between this derivation and the following one:

E ⇒ E+Ě ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a

We want to characterize two derivations as "coming from the same parse tree."

The first step is to define the relation among derivations as being "more left-oriented at one step". Assume we have two equal length derivations of length n > 2:

D: x1⇒ x2⇒ ... ⇒xn

D′: x1′ ⇒ x2′ ⇒ ... ⇒xn′

Where x1 = x1′ is a non-terminal and

xn = xn′ ∈ Σ*

Namely they start with the same non-terminal and end at the same terminal string and have at least two intermediate steps.

Let’s say D < D′ if the two derivations differ in only one step in which there are 2 non-terminals, A and B, such that D replaces the left one before the right one and D′ does the opposite. Formally:

D < D′ if there exists k, 1 < k < n such that

xi = xi′ for all i ≠ k (equal strings, same marked position)

xk-1 = uǍvBw, for u, v, w ∈ V*

xk-1′ = uAvB̌w, for u, v, w ∈ V*

xk =uyvB̌w, for production A → y

xk′ = uǍvzw, for production B → z

xk+1 = xk+1′ = uyvzw (marking not shown)

Two derivations are said to be similar if they belong to the reflexive, symmetric, transitive closure of <.

2.5 Ambiguity in CFG

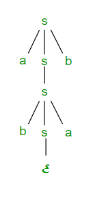
Suppose we have a context free grammar G with production rules: S->aSb|bSa|SS|ɛ

Left most derivation (LMD) and Derivation Tree:

Leftmost derivation of a string from staring symbol S is done by replacing leftmost non-terminal symbol by RHS of corresponding production rule.

For example: The leftmost derivation of string abab from grammar G above is done as:

S =>aSb =>abSab =>abab

The symbols in bold are replaced using production rules.

Derivation tree: It explains how string is derived using production rules from S and is shown in Figure.

Figure Derivation tree

Right most derivation (RMD):

It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.

For Example: The rightmost derivation of string abab from grammar G above is done as:

S => SS =>SaSb =>Sab =>aSbab =>abab

The symbols in bold are replaced using production rules.

The derivation tree for abab using rightmost derivation is shown in Figure.

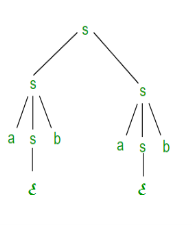
Ambiguity in Context free Grammar and Context free Languages2

Figure Right most derivation

A derivation can be either LMD or RMD or both or none. For Example:

S =>aSb =>abSab =>abab is LMD as well as RMD

butS => SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.

Ambiguous Context Free Grammar:

A context free grammar is called ambiguous if there exists more than one LMD or RMD for a string which is generated by grammar.

There will also be more than one derivation tree for a string in ambiguous grammar.

The grammar described above is ambiguous because there are two derivation trees.

There can be more than one RMD for string abab which are:

S => SS =>SaSb =>Sab =>aSbab =>abab

S =>aSb =>abSab =>abab

2.6 Pumping lemma for context-free languages

Lemma: The language 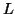= 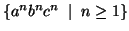$\{a^nb^nc^n\; \mid\; n \geq 1\}$ is not context free.

Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let 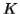$K$ be the constant of the Pumping Lemma.
Considering the string 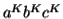$a^Kb^Kc^K$ , where 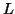$L$ is length greater than $K$ .
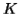By the Pumping Lemma this is represented as 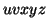$uvxyz$ , such that all 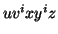$uv^ixy^iz$ are also in 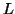$L$ , which is not possible, as:

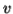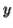either $v$ or $y$ cannot contain many letters from 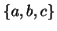$\{a,b,c\}$ ; else they are in the wrong order .

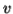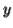if $v$ or $y$ consists of a's, b's or c's, then 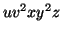$uv^2xy^2z$ cannot maintain the balance amongst the three letters.

Lemma: The language 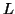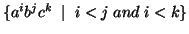$L$ = $\{a^ib^jc^k\; \mid\; i < j\; and\; i < k\}$ is not context free.

Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.

Let 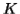$K$ be the constant of the Pumping Lemma.
Considering the string 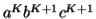$a^Kb^{K+1}c^{K+1}$ , which is $L$ > $K$ .
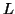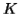By the Pumping Lemma this must be represented as 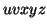$uvxyz$ , such that all 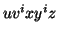$uv^ixy^iz$ are also in $L$ .

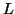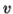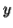-As mentioned previously neither $v$ nor $y$ may contain a mixture of symbols.

-Suppose 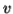$v$ consists of a's.
Then there is no way 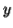$y$ cannot have b's and c's. It generate enough letters to keep them more than that of the a's (it can do it for one or the other of them, not both).
Similarly 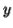$y$ cannot consist of just a's.

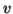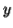-So suppose then that $v$ or $y$ contains only b's or only c's.
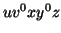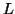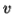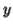Consider the string $uv^0xy^0z$ which must be in $L$ . Since we have dropped both $v$ and $y$ , we must have at least one b' or one c' less than we had in 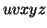$uvxyz$ , which was 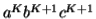$a^Kb^{K+1}c^{K+1}$ . Consequently, this string no longer has enough of either b's or c's to be a member of $L$ .

2.7 Deterministic pushdown automata

Machine transitions are based on the current state and input symbol, and also the current topmost symbol of the stack.

Symbols lower in the stack are not visible and have no immediate effect. Machine actions include pushing, popping, or replacing the stack top.

A deterministic pushdown automaton has at most one legal transition for the same combination of input symbol, state, and top stack symbol.

This is where it differs from the nondeterministic pushdown automaton.

2.8 Closure properties of CFLs

They are closed under −

Union

Concatenation

Kleene Star operation

Union

Let A1 and A2 be two context free languages. Then A1 ∪ A2 is also context free.

Example

Let A1 = { xnyn , n > 0}. Corresponding grammar G1 will have P: S1 → aAb|ab

Let A2 = { cmdm , m ≥ 0}. Corresponding grammar G2 will have P: S2 → cBb| ε

Union of A1 and A2, A = A1 ∪ A2 = { xnyn } ∪ { cmdm }

The corresponding grammar G will have the additional production S → S1 | S2

Concatenation

If A1 and A2 are context free languages, then A1A2 is also context free.

Example

Union of the languages A1 and A2, A = A1A2 = { anbncmdm }

The corresponding grammar G will have the additional production S → S1 S2

Kleene Star

If A is a context free language, then A* is also context free.

Example

Let A = { xnyn , n ≥ 0}. Corresponding grammar G will have P: S → aAb| ε

Kleene Star L1 = { xnyn }*

The corresponding grammar G1 will have additional productions S1 → SS1 | ε

Context-free languages are not closed under −

Intersection − If A1 and A2 are context free languages, then A1 ∩ A2 is not necessarily context free.

Intersection with Regular Language − If A1 is a regular language and A2 is a context free language, then A1 ∩ A2 is a context free language.

Complement − If A1 is a context free language, then A1’ may not be context free.

Reference books

1. Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.

2. Dexter C. Kozen, Automata and Computability, Undergraduate Texts in Computer Science, Springer.

3. Michael Sipser, Introduction to the Theory of Computation, PWS Publishing.

4. John Martin, Introduction to Languages and the Theory of Computation, Tata McGraw Hill.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined