UNIT 5
Undecidability
In 1936, a technique named as lambda-calculus was created by Alonzo Church within which the Church numerals area unit well outlined, i.e. the encryption of natural numbers. additionally in 1936, mathematician machines (earlier known as theoretical model for machines) was created by mathematician, that's used for manipulating the symbols of string with the assistance of tape.
Church mathematician Thesis :
Turing machine is outlined as associate degree abstract illustration of a computer like hardware in computers. mathematician planned Logical Computing Machines (LCMs), i.e. mathematician’s expressions for Turing Machines. This was done to outline algorithms properly. So, Church created a mechanical methodology named as ‘M’ for manipulation of strings by mistreatment logic and arithmetic.
This methodology M should pass the subsequent statements:
• Number of directions in M should be finite.
• Output ought to be made when playing finite variety of steps.
• It mustn't be imagined, i.e. is created in world.
• It mustn't need any complicated understanding.
Using these statements Church planned a hypothesis known as Church’s mathematician thesis that may be expressed as: “The assumption that the intuitive notion of estimable functions is known with partial algorithmic functions.”
In 1930, this statement was initial developed by Alonzo Church and is typically brought up as Church’s thesis, or the Church-Turing thesis. However, this hypothesis can not be proved .
The algorithmic functions is estimable when taking following assumptions:
1. every and each operate should be estimable.
2. Let ‘F’ be the estimable operate and when playing some elementary operations to ‘F’, it'll rework a replacement operate ‘G’ then this operate ‘G’ mechanically becomes the estimable operate.
3. If any operates that follow on top of 2 assumptions should be states as estimable function.
What Justifies the Church-Turing Thesis?
Stephen Kleenewho coined the term "Church-Turing thesis"catalogued four sorts of argument for CTT-O: initial, the argument from non-refutation points out the thesis has ne'er been refuted, despite sustained (and ongoing) makes an attempt to search out a disproof (such because the makes an attempt by László Kalmár and, additional recently, by Doukas Kapantais). Second, the argument from confluence points to the very fact that the assorted characterizations of computability, whereas differing in their approaches and formal details, end up to comprehend the exact same category of estimable functions. Four such characterizations were bestowed (independently) in 1936 and like a shot proved to be extensionally equivalent: mathematician computability, Church's -definability, Kleene's algorithmic functions, and Post's finitary combinatory processes.
Third is associate degree argument typically brought up today as "Turing's analysis." mathematician known as it merely argument "I," stating 5 terribly general and intuitive constraintsor axiomsthe human pc is also assumed to satisfy: "The behavior of the pc at any moment is set by the symbols that he's perceptive, associate degreed his 'state of mind' at that moment"; "[T] here may be a sure B to {the variety|the amount|the quantity} of images or squares that the pc will observe at one moment"; "[E]ach of the new discovered squares is at intervals L squares of an like a shot antecedently discovered square"; "[I]n a straightforward operation no more than one symbol is altered"; and "[T]he number of states of mind which require be taken under consideration is finite." mathematician noted that relation to the computer's states of mind is avoided by talking instead concerning configurations of symbols, these being "a additional definite and physical counterpart" of states of mind.
The second a part of mathematician's argument I may be a demonstration that every operate computed by any human pc subject to those constraints is additionally estimable by a computing machine; it's not tough to visualize that every of the computer's steps is mimicked by the Turing machine, either during a single step or by means that of a series of steps. In short, Turing's 5 axioms entail CTT-O. (Turing's axiomatic approach to computability was actually foreshadowed by Kurt Gödel during a suggestion to Church a year about earlier. Some more moderen axiomatic approaches to computability proceed differently; as an example, Erwin Engeler employs the Schönfinkel-Curry plan of "combinators" so as to axiomatize the idea of associate degree recursive operate.)
Fourth during this catalog of issues supporting CTT-O area unit arguments from first-order logic. they're typified by a 1936 argument of Church's and by Turing's argument II, from Section nine of Turing's 1936 paper. In 2013, Saul Kripke bestowed a reconstruction of Turing's argument II, which works as follows: Computation may be a special variety of mathematical deduction; each|and each} mathematical deductionand thus every computationcan be formalized as a legitimate deduction within the language of first-order predicate logic with identity (a step Kripke brought up as "Hilbert's thesis"); following Gödel's completeness theorem, every computation is so formalized by a obvious formula of first-order logic; and each computation will thus be disbursed by the universal computing machine. This last step concerning the universal computing machine is secured by a theorem proved by Turing: each obvious formula of first-order logic is proved by the universal computing machine.
The third and fourth of those arguments offer justification for CTT-O however not for CTT-A. As Robin Gandy found out, the third argumentTuring's Icontains "crucial steps ... wherever he [Turing] appeals to the very fact that the calculation is being disbursed by a person's being." as an example, mathematician assumed "a soul will solely write one image at a time," associate degreed Gandy noted this assumption can not be carried over to a parallel machine that "prints an discretionary variety of symbols at the same time." In Conway's Game of Life, for example, there's no edge on the amount of cells that conjure the grid, nevertheless the symbols altogether the cells area unit updated at the same time. Likewise, the fourth argument (Turing's II) involves the claim that computation may be a special variety of formal proof, however the notion of proof is in and of itself associated with what a person's mathematicianand not some oraclecan prove.
It is thus perhaps not too surprising that the third and fourth arguments in this catalog seldom if ever appear in logic and computer science textbooks. The two arguments that are always given for the Church-Turing thesis (in, for example, Lewis and Papadimitriou are confluence and non-refutation. Yet both those arguments are merely inductive, whereas the third and fourth arguments are deductive in nature.
However, a number of attempts have sought to extend Turing's axiomatic analysis to machine computation; for example, Gandy broadened Turing's analysis in such a way that parallel computation is included, while Dershowitz and Gurevich gave a more general analysis in terms of abstract state machines. We return to the topic of extending the analysis to machine computation later in this article but first address the important question of whether CTT-O is mathematically provable.
A Turing Machine is the mathematical tool equivalent to a digital computer. It was suggested by the mathematician Turing in the 30s, and has been since then the most widely used model of computation in computability and complexity theory.
The model consists of an input output relation that the machine computes. The input is given in binary form on the machine's tape, and the output consists of the contents of the tape when the machine halts.
What determines how the contents of the tape change is a finite state machine (or FSM, also called a finite automaton) inside the Turing Machine. The FSM is determined by the number of states it has, and the transitions between them.
At every step, the current state and the character read on the tape determine the next state the FSM will be in, the character that the machine will output on the tape (possibly the one read, leaving the contents unchanged), and which direction the head moves in, left or right.
The problem with Turing Machines is that a different one must be constructed for every new computation to be performed, for every input output relation.
This is why we instroduce the notion of a universal turing machine (UTM), which along with the input on the tape, takes in the description of a machine M. The UTM can go on then to simulate M on the rest of the contents of the input tape. A universal turing machine can thus simulate any other machine. 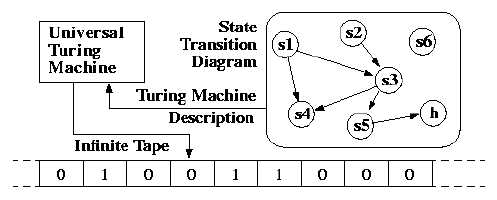
I learned about Turing Machines the first term of my sophomore year at MIT (Fall 96), in 6.004 (Computational Structures), the best class ever conceived. It was late one night when I was starting my problem set on writing a turing machine to compute some operation. To test my result, I figured I could code up a Universal Turing Machine in Scheme to help me do my problem set. I could then feed it my description and a sample input, and it would simulate any machine for me. To my surprise within two hours, the program was working, and i could start the rest of my problem set
;; Program used to check solutions to a 6.004 problem set
;; Simulation of a Turing machine
;; global variables used by procedures.
;; Those are changed at every step, and must be reinitialized before running a different
;; example, by running: (setup state-graph tape initial-state initial-position)
(define *machine* '()) ; the machine currently running
(define *state* 's1) ; the state at which the current machine is at
(define *position* 0) ; the position at which the tape is reading
(define *tape* #()) ; the tape that the current machine is currently running on
;; The following procedure takes in a state graph (see examples below), and turns it
;; to a machine, where each state is represented only once, in a list containing:
;; a structure of the form:
;; ((state (in out move next-state) (in out move next-state) (in out move next-state))
;; (state2 (in out move next-state))
;; (state3 (in out move next-state) (in out move next-state)))
;;
;; Each state name is followed by a list of combinations of inputs (read on the tape)
;; and the corresponding output (written on the tape), direction of motion (left or right),
;; and next state the machine will be in.
;;
;; Here's the machine returned by (initialize flip) (as defined at the end of this file)
;;
;; ((s4 (0 0 l h))
;; (s3 (1 1 r s4) (0 0 l s3))
;; (s2 (0 1 l s3) (1 0 r s2))
;; (s1 (0 1 r s2) (1 1 l s1)))
(define (initialize state-graph)
(define (extend machine states-to-go)
(if (null? states-to-go)
machine
(let ((cur-state (first states-to-go))
(matched #f))
(extend (begin (for-each (lambda (state)
(if (equal? (state-name state) (car cur-state))
(begin (set! matched #t)
(set-cdr! state (cons (cdr cur-state) (cdr state))))))
machine)
(if matched
machine
(cons (list (state-name cur-state)
(cdr cur-state))
machine)))
(cdr states-to-go)))))
(extend '() state-graph))
;; Setup is a handy procedure to initialize and test a new graph.
;; It will take care of reading the graph, and initializing the global variables.
;; Once this is done, all one has to do is run the program (run) or move step
;; by step (step) for debugging
(define (setup state-graph tape state position)
(set! *machine* (initialize state-graph))
(set! *tape* tape)
(set! *state* state)
(set! *position* position))
;; The following are the procedures that implement the Turing machine.
;; It can write, read, move, etc...
(define (set-state! state)
(set! *state* state))
(define (set-position! position)
(set! *position* position))
(define (do-move move-to-make)
(cond ((equal? move-to-make 'R) (move-right))
((equal? move-to-make 'L) (move-left))
(else (error "i don't know what move to make: " move-to-make))))
(define (move-right)
(set! *position* (+ *position* 1)))
(define (move-left)
(set! *position* (- *position* 1)))
(define (write output)
(vector-set! *tape* *position* output))
(define (read)
(vector-ref *tape* *position*))
;; The following Constructors and selectors implement the data
;; structures used by the program.
;; A State is: '(s1 (0 1 r s2) (1 1 l s1))
;; (see above)
(define state-name car)
(define state-specs cdr) ;; returns ==> '((0 1 r s2) (1 1 l s1))
;; (a list of specs)
;; spec is: (input output move next-state)
;; It specifies for a given input, the output, direction of motion and
;; next state.
(define spec-input car)
(define spec-result cdr)
;; result is: (output move next-state)
;; These are all the things we have to deduce from state and input,
;; to be able to continue in our program.
(define result-output car)
(define result-move cadr)
(define result-state caddr)
;; This procedure looks through our *machine* to find the state
;; whose name it is given, and it returns the state with all
;; of its specifications.
(define (get-state-by-name name)
(define (helper states-to-go)
(if (null? states-to-go)
(error "Reference to undefined state" name)
(if (equal? (state-name (car states-to-go)) name)
(car states-to-go)
(helper (cdr states-to-go)))))
(helper *machine*))
;; This procedure is called with the output from the previous procedure (a state)
;; and an input (read from the tape), and it returns the actions to perform
;; (what to write, where to move, which state to go to), in the form:
;; (current-state (output direction-of-motion next-state))
(define (get-what-to-do state input)
(define (helper specs-to-go input)
(if (null? specs-to-go)
(error "Unspecified input to state encountered\n You haven't told me what to do in state"
(state-name state) 'with 'input input)
(if (equal? (spec-input (car specs-to-go)) input)
(list (state-name state) (spec-result (car specs-to-go)))
(helper (cdr specs-to-go) input))))
(helper (state-specs state) input))
;; example:
;; (get-what-to-do (get-state-by-name 's1) 0)
;; ;Value: (s1 (1 r s2))
;; the following selectors deal with the output of get-what-to-do
;; what-to-do is of the form: (current-state (output move next-state))
(define what-to-output caadr)
(define where-to-move cadadr)
(define (what-next-state what-to-do)
(car (cddadr what-to-do)))
;; Sending output (for the user to know what's going on)
(define (describe-move input output move state)
(newline)
(display (list 'input: input 'output: output 'move: move 'state: state 'position: *position* ':
(read))))
(define (describe-current-position)
(newline)
(display (list *tape* *state* *position* (read))))
(define (return-current-position)
(list *tape* *position* *state*))
;; and here are the procedures that make everything work
;; Once the global variables are set appropriately (either automatically by
;; running (setup ...) or manually (for debugging), calling the procedure
;; (step) will make the Turing machine perform one action.
(define (step)
(let* ((what-to-do (get-what-to-do (get-state-by-name *state*) (read)))
(output (what-to-output what-to-do))
(move (where-to-move what-to-do))
(state (what-next-state what-to-do)))
; (describe-move input result output move state)
(write output)
(do-move move)
(set-state! state)
(describe-current-position)))
;; All (run) is doing is calling (step) until the state is "halt" (here 'h)
(define (run)
(if (equal? *state* 'h)
(return-current-position)
(begin (step) (run))))
;; And here are the actual tests relevant to the problem set
;; flip flips a unary number 01111110 to 10000001.
(define flip
'(
(s1 1 1 L s1)
(s1 0 1 R s2)
(s2 1 0 R s2)
(s2 0 1 L s3)
(s3 0 0 L s3)
(s3 1 1 R s4)
(s4 0 0 L H)))
(define tape1
(list->vector '(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _)))
;; We will run the test on tape1 (above), starting in state s1, and in position 17 of the tape (arbitrary choice)
(setup flip tape1 's1 17)
(run)
;; Here's the output:
;; (i've taken the liberty of erasing the lines where the pointer only was moving, without changing the
;; inputs, outputs, state, but only the position on the tape (as you can notice on the rightmost part of the output).
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s1 16)
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s1 7)
;; (#(_ _ _ _ _ _ _ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 8)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 9)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 10)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 11)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 12)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 13)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 14)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 15)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 16)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 17)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 18)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 19)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 20)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 21)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 22)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 23)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 24)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 25)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s2 26)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s3 25)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s3 7)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) s4 8)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) h 7)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) h 7)
;Value: (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _) 7 h)
;; this is the second A of problem 1
;; It takes a unary number, and doubles it: 011110 -> 0111111110
(define doubler
'(
(s1 1 1 L s1)
(s1 0 1 R s2)
(s2 1 0 R s3)
(s2 0 0 L s8)
(s3 0 0 R s4)
(s3 1 1 R s3)
(s4 _ 1 L s5)
(s4 1 1 R s4)
(s5 0 0 L s6)
(s5 1 1 L s5)
(s6 0 0 R s8)
(s6 1 1 L s7)
(s7 0 0 R s2)
(s7 1 1 L s7)
(s8 0 0 R s8)
(s8 1 0 R s8)
(s8 _ 0 L s9)
(s9 0 0 L s10)
(s10 0 1 L s10)
(s10 1 0 R s11)
(s11 0 0 L H)
(s11 1 1 L H)))
(define tape2
(list->vector '(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _)))
(setup doubler tape2 's1 11)
(run)
;; Here's the output (with the same criteria as above for erasing lines).
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s1 10 1)
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s1 7 0)
;; (#(_ _ _ _ _ _ _ 1 1 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s2 8 1)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s3 9 1
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 0 _ _ _ _ _ _ _ _ _ _ _) s4 15 _)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 0 1 _ _ _ _ _ _ _ _ _ _) s5 14 0)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 0 1 _ _ _ _ _ _ _ _ _ _) s2 9 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 0 1 _ _ _ _ _ _ _ _ _ _) s3 10 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 0 1 _ _ _ _ _ _ _ _ _ _) s4 16 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 0 1 1 _ _ _ _ _ _ _ _ _) s5 15 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 0 1 1 _ _ _ _ _ _ _ _ _) s2 10 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 0 1 1 _ _ _ _ _ _ _ _ _) s3 11 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 0 1 1 _ _ _ _ _ _ _ _ _) s4 17 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 0 1 1 1 _ _ _ _ _ _ _ _) s5 16 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 0 1 1 1 _ _ _ _ _ _ _ _) s2 11 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 0 1 1 1 _ _ _ _ _ _ _ _) s3 12 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 0 1 1 1 _ _ _ _ _ _ _ _) s4 18 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 0 1 1 1 1 _ _ _ _ _ _ _) s5 17 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 0 1 1 1 1 _ _ _ _ _ _ _) s2 12 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 0 1 1 1 1 _ _ _ _ _ _ _) s3 13 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 0 1 1 1 1 _ _ _ _ _ _ _) s4 19 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 0 1 1 1 1 1 _ _ _ _ _ _) s5 18 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 0 1 1 1 1 1 _ _ _ _ _ _) s2 13 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 _ _ _ _ _ _) s3 14 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 _ _ _ _ _ _) s4 20 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 1 _ _ _ _ _) s5 19 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 1 _ _ _ _ _) s8 15 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 1 1 1 1 1 _ _ _ _ _) s8 16 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 1 1 1 1 _ _ _ _ _) s8 17 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 1 1 1 _ _ _ _ _) s8 18 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 1 1 _ _ _ _ _) s8 19 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 1 _ _ _ _ _) s8 20 1)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 _ _ _ _ _) s8 21 _)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 _ _ _ _) s9 20 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 _ _ _ _) s10 19 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 _ _ _ _) s10 18 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 _ _ _ _) s10 17 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 _ _ _ _) s10 16 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 0 1 1 1 1 0 0 _ _ _ _) s10 15 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 0 1 1 1 1 1 0 0 _ _ _ _) s10 14 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 0 1 1 1 1 1 1 0 0 _ _ _ _) s10 13 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 0 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 12 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 0 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 11 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 0 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 10 0)
;; (#(_ _ _ _ _ _ _ 1 0 0 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 9 0)
;; (#(_ _ _ _ _ _ _ 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 8 0)
;; (#(_ _ _ _ _ _ _ 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s10 7 1)
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) s11 8 1)
;; (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) h 7 0)
;; ;Value: (#(_ _ _ _ _ _ _ 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 _ _ _ _) 7 h)
The resolving Language
1. Reducing One drawback to a different
Suppose we've Associate in Nursing algorithmic program A to rework instances of 1 drawback P1 to instances of another drawback P2 in such the way that a string w is in P1 if and on condition that the reworked string A(w) is in P2. What this means is that we are able to solve instances of drawback P1 by changing them to instances of drawback P2 so mistreatment the answer to drawback P2 to answer the first question. If we are able to try this, then we are going to say that A may be a reduction of P1 to P2.
Note that a discount from P1 to P2 should flip each instance of P1 with a affirmative Associate in Nursingswer to an instance of P2 with a affirmative answer, and each instance of P1 with a no Associate in Nursingswer to an instance of P2 with a no answer.
we are going to oftentimes use this method to point out that drawback P2 is as exhausting as drawback P1.
The direction of the reduction is very important.
for instance, if there's a discount from P1 to P2 and if P1 isn't algorithmic, then P2 can not be algorithmic. (Why?)
Similarly, if there's a discount from P1 to P2 and if P1 isn't recursively calculable, then P2 can not be recursively calculable. (Why?)
2. Enumerating the Binary Strings
In several proofs involving Alan Mathison Turing machines, we'd like to enumerate the binary strings and encipher computing machines in order that WIll|we are able to} seek advice from the ith binary string as wi and also the ith Alan Mathison Turing machine as Mi.
The binary strings area unit straightforward to enumerate. If w may be a binary string, we have a tendency to shall treat 1w because the binary number i thus we are able to decision w the ith string.
mistreatment this coding, the empty string is that the 1st string, zero the second, one the third, 00 the fourth, 01 the fifth, and so on. henceforward WIll|we'll|we are going to} seek advice from the ith string as wi.
3. Codes for Alan Mathison Turing machines
we are going to currently outline a code for all Alan Mathison Turing machines with the input alphabet in order that every computing machine may be painted by a binary string. this may enable United States to speak regarding the ith computing machine as Mi. we are going to adopt the subsequent conventions:
we have a tendency to assume the states area unit q1, q2, . . . , qr for a few r. we have a tendency to assume q1 can continually be the beginning state. we have a tendency to assume q2 are going to be the sole acceptive state. we'd like only 1 acceptive state if we have a tendency to assume the computing machine halts whenever it enters Associate in Nursing acceptive state.
we have a tendency to assume the tape symbols area unit X1, X2, . . . , Xs for a few s. we have a tendency to assume X1 is zero, X2 is 1, and X3 is that the blank.
we have a tendency to assign integers D1 and D2 to the tape head directions left and right.
currently we are able to encipher a transition rule δ(qi, Xj) = (qk, Xl, Dm) as a binary string C of the shape
0i10j10k 10l10m
Suppose there area unit n transition rules. The code for the complete computing machine are going to be the concatenation of the codes for all of the transitions (in some order) separated by pairs of 1's:
C111C211 … Cn-111Cn
Note that there may be several encodings for identical computing machine.
we are able to encipher a try (Mi, w) consisting of a computing machine and a string by appending 111 to the coding of the computing machine so appending the string w.
4. The resolving Language Ld isn't Recursively calculable
we have a tendency to outline Ld, the resolving language, as follows:
Let w1, w2, w3, . . . be Associate in Nursing enumeration of all binary strings.
Let M1, M2, M3, . . . be Associate in Nursing enumeration of all Alan Mathison Turing machines.
Let Ld = American state | Wisconsin isn't in L(Mi) }.
Theorem: Ld isn't a recursively calculable language.
Proof:
Suppose Ld = L(Mi) for a few atomic number 69 Mi.
this offers rise to a contradiction. take into account what Mi can do on Associate in Nursing input string Wisconsin.
If Mi accepts Wisconsin, then by definition Wisconsin can not be in Ld.
If Mi doesn't accepts Wisconsin, then by definition Wisconsin is in Ld.
Since Wisconsin will neither be in Ld nor not be in Ld, we have a tendency to should conclude there's no computing machine which will outline Ld.
Identifying languages (or problems*) as decidable, undecidable or part decidable may be a quite common question in GATE. With correct data and ample expertise, this question becomes terribly straightforward to unravel.
Lets begin with some definitions:-
Decidable language -A call drawback P is claimed to be decidable (i.e., have Associate in Nursing algorithm)
if the language L of all affirmative instances to P is decidable.
Example- (I) (Acceptance drawback for DFA) Given a DFA will it settle for a given
word?
(II) (Emptiness drawback for DFA) Given a DFA will it settle for any word?
(III) (Equivalence drawback for DFA) Given 2 DFAs, do they settle for the
same language?
Undecidable language -– a call drawback P is claimed to be undecidable if the language L of all
yes instances to P isn't decidable or a language is undecidable if it's not decidable. Associate in Nursing undecidable language perhaps a part decidable language or one thing else however not decidable. If a language isn't even part decidable , then there exists no computing machine for that language.
Partially decidable or Semi-Decidable Language -– a call drawback P is claimed to be semi-decidable (i.e., have a semi-algorithm) if the language L of all affirmative instances to P is RE. A language ‘L’ is part decidable if ‘L’ may be a RE however not REC language.
Recursive language(REC) – A language ‘L’ is alleged to be algorithmic if there exists a computing device which is able to settle for all the strings in ‘L’ and reject all the strings not in ‘L’. The computing device can halt on every occasion and provides associate answer(accepted or rejected) for every and each string input. A language ‘L’ is decidable if it's a algorithmic language. All decidable languages area unit algorithmic languages and vice-versa.
Recursively countable language(RE) – A language ‘L’ is alleged to be a recursively countable language if there exists a computing device which is able to settle for (and so halt) for all the input strings that area unit in ‘L’ however could or might not halt for all input strings that aren't in ‘L’. By definition , all REC languages {are also|also area unit|are} RE languages however not all RE languages are REC languages.
Now lets solve some examples –
a method to unravel decidability issues is by {trying|making associate attempt|attempting} to cut back an already illustrious undecidable downside to the given downside. By reducing a retardant P1 to P2, we tend to mean that we tend to try to unravel P1 by mistreatment the formula wont to solve P2.
If we are able to cut back associate already illustrious undecidable downside P1 to a given downside P2 , then we are able to sure enough say that P2 is additionally undecidable. If P2 was decidable, then P1 would even be decidable however that becomes a contradiction as a result of P1 is understood to be undecidable.
For eg.
1. Given a computing device ‘M’, we want to seek out out whether or not a state ‘Q’ is ever reached once a string ‘w’ is entered in ‘M’. This downside is additionally referred to as the ‘State Entry problem’.
Now lets try and cut back the Halting downside to the State Entry downside. A computing device solely halts once a transition operate ? (qi , a) isn't outlined. modification each indefinable operate ?(qi,a) to ?(qi,a) = (Q, a, L or R). Note that the state letter will solely be reached once the computing device halts.
Suppose we've have associate formula for finding the State Entry downside which is able to halt on every occasion and tell United States of America whether or not state letter will be reached or not. By telling United States of America that we are able to or cannot reach state letter on every occasion, it's telling United States of America that the computing device can or won't halt, every time. however we all know that's impractical as a result of the halting downside is undecidable. meaning that our assumption that there exists associate formula that solves the State Entry downside and halts and offers United States of America a solution on every occasion, is false. Hence, the state entry downside is undecidable.
2. Given 2 regular languages L1 and L2, is that the downside of finding whether or not a string ‘w’ exists in each L1 and L2, a decidable downside or not.
First we tend to create 2 mathematician machines TM1 and TM2 that simulate the DFAs of languages L1 and L2 severally. we all know that a DFA continuously halts, therefore a computing device simulating a DFA will continuously halt. we tend to enter the string ‘w’ in TM1 and TM2. each mathematician machines can halt and provides United States of America a solution. we are able to connect the outputs of the {turing|Turing|Alan mathematician|Alan Mathison Turing|mathematician} machines to a changed ‘AND’ gate which is able to output ‘yes’ only each the Turing machines answer ‘yes’. Otherwise it'll output ‘no’.
Since this method of 2 mathematician machines and a changed AND gate can continuously stop, this downside may be a decidable downside.
There area unit heaps of queries on this subject. there's no universal formula to unravel them. Most of the queries need distinctive and ingenious proofs. Here is wherever expertise is required. By finding heaps of those issues, one will become terribly fast in developing with proofs for these issues on the spot. So, keep active.
*The words ‘language’ and ‘problem’ will be used synonymously in Theory of computation. For eg. The ‘Halting problem’ can even be written as ‘L = { | computing device ‘M’ halts on input ‘w’}’. Here ‘L’ may be a language.
Rice theorem states that any non-trivial linguistics property of a language that is recognized by a information processing system is undecidable. A property, P, is that the language of all Alan Mathison Turing machines that satisfy that property.
Formal Definition
If P may be a non-trivial property, and therefore the language holding the property, Lp , is recognized by information processing system M, then record = L(M) ∈ P is undecidable.
Description and Properties
• Property of languages, P, is solely a collection of languages. If any language belongs to P (L ∈ P), it's aforesaid that L satisfies the property P.
• A property is named to be trivial if either it's not happy by any recursively numerable languages, or if it's happy by all recursively numerable languages.
• A non-trivial property is happy by some recursively numerable languages and aren't happy by others. Formally speaking, in an exceedingly non-trivial property, wherever L ∈ P, each the subsequent properties hold:
o Property one one There exists Alan Mathison Turing Machines, M1 and M2 that acknowledge constant language, i.e. either ( , ∈ L ) or ( , ∉ L )
o Property two two There exists Alan Mathison Turing Machines M1 and M2, wherever M1 acknowledges the language whereas M2 doesn't, i.e. ∈ L and ∉ L
Proof
Suppose, a property P is non-trivial and φ ∈ P.
Since, P is non-trivial, a minimum of one language satisfies P, i.e., L(M0) ∈ P , ∋ information processing system M0.
Let, w be associate degree input in an exceedingly specific instant and N may be a information processing system that follows −
On input x
• Run M on w
• If M doesn't settle for (or does not halt), then don't settle for x (or don't halt)
• If M accepts w then run M0 on x. If M0 accepts x, then settle for x.
A perform that maps associate degree instance ATM = M accepts input w to a N such
• If M accepts w and N accepts constant language as M0, Then L(M) = L(M0) ∈ p
• If M doesn't settle for w and N accepts φ, Then L(N) = φ ∉ p
Since ATM is undecidable and it is reduced to record, record is additionally undecidable.
Decidable issues
A problem is decidable if we will construct a information processing system which can halt in finite quantity of your time for each input and provides answer as ‘yes’ or ‘no’. A decidable downside has associate degree formula to work out the solution for a given input.
Examples
• Equivalence of 2 regular languages: Given 2 regular languages, there's associate degree formula and information processing system to make a decision whether or not 2 regular languages ar equal or not.
• Finiteness of normal language: Given an everyday language, there's associate degree formula and information processing system to make a decision whether or not regular language is finite or not.
• Emptiness of context free language: Given a context free language, there's associate degree formula whether or not CFL is empty or not.
Undecidable issues
A problem is undecidable if there's no information processing system which can continuously halt in finite quantity of your time to provide answer as ‘yes’ or ‘no’. associate degree undecidable downside has no formula to work out the solution for a given input.
Examples
• Ambiguity of context-free languages: Given a context-free language, there's no information processing system which can continuously halt in finite quantity of your time and provides answer whether or not language is ambiguous or not.
• Equivalence of 2 context-free languages: Given 2 context-free languages, there's no information processing system which can continuously halt in finite quantity of your time and provides answer whether or not 2 context free languages ar equal or not.
• Everything or completeness of CFG: Given a CFG and input alphabet, whether or not CFG can generate all doable strings of input alphabet (∑*)is undecidable.
• Regularity of CFL, CSL, REC and REC: Given a CFL, CSL, REC or REC, determinative whether or not this language is regular is undecidable.
Note: 2 in style undecidable issues ar halting downside of metal and angel dust (Post Correspondence Problem). Semi-decidable issues
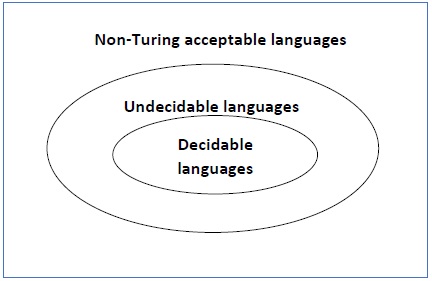
A semi-decidable downside is set of undecidable issues that information processing system can continuously halt in finite quantity of your time for answer as ‘yes’ and will or might not halt for answer as ‘no’.
Relationship between semi-decidable and decidable downside has been shown in Figure one as:
Rice’s Theorem
Every non-trivial (answer isn't known) downside on algorithmic numerable languages is undecidable.e.g.; If a language is algorithmic numerable, its complement are going to be algorithmic numerable or not is undecidable.
Reducibility and Undecidability
Language A is reducible to language B (represented as A≤B) if there exists a perform f which can convert strings in an exceedingly to strings in B as:
w ɛ A <=> f(w) ɛ B
Theorem 1: If A≤B and B is decidable then A is additionally decidable.
Theorem 2: If A≤B and A is undecidable then B is additionally undecidable.
For an undecidable language, there is no Turing Machine which accepts the language and makes a decision for every input string w (TM can make decision for some input string though). A decision problem P is called “undecidable” if the language L of all yes instances to P is not decidable. Undecidable languages are not recursive languages, but sometimes, they may be recursively enumerable languages.
Example
Books
John E. Hopcroft, Rajeev Motwani and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Pearson Education Asia.
Reference books
1. Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson EducationAsia.
2. Dexter C. Kozen, Automata and Computability, Undergraduate Texts in Computer Science, Springer.
3. Michael Sipser, Introduction to the Theory of Computation, PWS Publishing.
4. John Martin, Introduction to Languages and the Theory of Computation, Tata McGraw Hill.