Unit - 1
Security Services
A processing or communication service that improves the security of an organization's data processing systems and information transfers. These services are designed to protect against security attacks and rely on one or more security mechanisms to do so. The five categories of these services are as follows:
![[m1-2]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642700728_564713.jpeg)
Authentication is the process of verifying that the communicating entity is who it claims to be.
Peer Entity Authentication: Used in conjunction with a logical connection to ensure that the entities connecting are who they say they are.
Data-Origin Authentication: Provides assurance that the source of received data is as declared in a connectionless transmission.
Data Confidentiality: Prevents unauthorized disclosure of data.
Unauthorized usage of a resource is prevented via access control (i.e., this service controls who can have access to a resource, under what conditions access can occur, and what those accessing the resource are allowed to do).
Data Integrity: The certainty that data received is exactly as it was supplied by a legitimate source.
Non-repudiation: Prevents one of the parties participating in a communication from denying that they participated in all or part of it.
Proof of Origin: Evidence that the message was sent by the intended recipient.
Proof of Delivery: Evidence that the communication was delivered to the intended recipient.
To support these services, a variety of cryptographic and non-cryptographic techniques might be used. While a single cryptographic mechanism may be capable of providing multiple services, it cannot supply all of them.
Confidentiality
The property of confidentiality is essential when keeping information from being disclosed to unauthorized persons.
Cryptography is used to encrypt the data, making it unreadable to anybody except those who have been given permission to see it. To ensure confidentiality, the cryptographic technique and mode of operation must be designed and implemented in such a way that an unauthorized person will be impossible to deduce the encryption keys or extract the information without utilizing the necessary keys.
Integrity of Data
Data integrity ensures that data has not been tampered with after it has been created, transmitted, or stored in an illegal manner. This indicates that the data has not been inserted, deleted, or substituted.
Digital signatures, also known as message authentication codes, are cryptographic procedures that can be used to detect both unintentional and malicious alterations, such as those caused by device failure or transmission difficulties. While non-cryptographic procedures can be used to detect unintentional changes, cryptographic mechanisms cannot. They are ineffective at identifying deliberate changes.
Authentication services can be provided via cryptography in two ways:
- Integrity authentication can be used to ensure that the data has not been tampered with.
- Source authentication can be used to validate the identity of the person or machine who created the data.
Authentication services are frequently provided using digital signatures or message authentication codes. This service could also be provided via key-agreement mechanisms.
Authorization
Permission to conduct a security function or action is granted through authorization. A cryptographic service is frequently used to support this security service.
Non-Repudiation
Non-repudiation is a word used in key management to describe the binding of a certificate subject to a public key using digital signature keys and digital certificates. When a digital signature key needs to be non-repudiable, it means that the signature created by that key is protected by both the integrity and source authentication services provided by a digital signature. In the same way that a document with a handwritten signature would, a digital signature can likewise signify a commitment by the certificate subject. However, there are numerous factors to consider when making a legal decision about non-repudiation, and this cryptographic process is simply one of them.
Services of Assistance
Supporting services are frequently required for the cryptographic security services listed above. A cryptographic service, for example, may frequently require services for key establishment, random number generation, and cryptographic key protection.
Bringing Services Together
It is strongly recommended that you use a combination of the six security services listed above. When creating a secure system, designers typically start by identifying which security systems are required to safeguard the data that will be stored and processed by the system. The mechanisms that would best supply these services are explored when the services have been determined.
It's possible that some of the mechanisms employed aren't cryptographic in nature. Physical security measures like identity badges or biometric identification devices, for example, can be used to block access to certain data for confidentiality reasons. Cryptographic mechanisms, on the other hand, which include algorithms, The most cost-effective means for keeping information safe are usually keys or other key material.
Attacks, Services, and Mechanisms in Security
To properly assess an organization's security needs, the security manager requires a systematic method of identifying security requirements and characterization of alternatives to meet those criteria. Consider the following three dimensions of information security:
Any activity that jeopardizes the security of an organization's information is referred to as a security attack.
A security mechanism is a system that detects, prevents, or recovers from a security breach.
Security service - A service that improves the security of an organization's data processing systems and information flows. The services are designed to thwart security attacks, and they employ one or more security measures to do so.
To effectively assess an organization's security needs and evaluate and pick alternative security products and policies, the security manager needs a systematic means of identifying security requirements and categorizing approaches to meeting those requirements.
To efficiently examine and evaluate an organization's security needs The OSI security architecture was created in conjunction with the OSI protocol architecture, which may be found in Appendix H. However, a comprehension of the OSI protocol architecture is not necessary for the purposes of this chapter. The OSI security architecture is a good fit for our needs.
The OSI security architecture gives a useful, albeit abstract, summary of many of the ideas for our needs. Security attacks, mechanisms, and services are the emphasis of the OSI security architecture. These can be summarized as follows:
Threat When a scenario, capacity, action, or event exists that has the potential to breach security and inflict harm, it is referred to as a potential for security violation.
In other words, a threat is a potential hazard that could exploit a weakness.
Attack
An intelligent act that is a deliberate attempt (especially in the sense of a method or technique) to evade security services and violate the security policy of a system; that is, an intelligent act that is a deliberate attempt (especially in the sense of a method or technique) to evade security services and violate the security policy of a system.
A communication must be transmitted from one party to another across the internet. For the exchange to take place, the two parties who are the transaction's principals must work together. By designating a path over the internet from source to destination and cooperating with communication protocols, a logical information channel can be built. (For example, TCP/IP) between the two principals.
Using this model necessitates that we:
Devise a suitable security transformation algorithm
Produce the algorithm's secret information (keys) build means for distributing and sharing the secret information establish a protocol that allows the principals to utilize the transformation and secret information for a security service referred to as traditional /single-key / private-key
A common key is shared by both the sender and the recipient.
Prior to the advent of public-key encryption in 1970, all classical encryption techniques were private-key only.
Plaintext - the message as it was originally sent
The following are some of the most commonly used terminologies:
Ciphertext - a message that has been encoded
Key - information used in encryption that is exclusively known by the sender/receiver
Cypher - algorithm for converting plaintext to ciphertext
Cryptography - the study of encryption principles and procedures
Encipher (encrypt) - converting plaintext to ciphertext decipher (decrypt) - recovering ciphertext from plaintext
The study of principles/methods for deciphering ciphertext without knowing the key is known as cryptanalysis (codebreaking).
The field of cryptography and cryptanalysis is known as cryptology.
Crypt text is a term for random nonsense. An algorithm and a key are used in the encryption process. The key is a value that isn't related to the plaintext. Changing the key alters the algorithm's output. It is possible to send the cypher text once it has been created. Using a decryption technique and the same key that was used for encryption, the cypher text can be converted back to the original plaintext upon receipt. Several things influence security. First, the encryption technique must be powerful enough that decrypting a communication only on the basis of cypher text is unfeasible. Beyond that, the key's secrecy determines the level of security. The algorithm's secret, not the algorithm's secrecy
There are two conditions for using symmetric encryption safely:
a powerful cryptographic algorithm
a secret key that is only known by the sender and receiver
EK = Y (X)
DK = X (Y)
Assume you know the encryption algorithm.
Implies the use of a secure route for key distribution.
There are five components to a symmetric encryption method.
• Plaintext: The original, understandable message or data that is sent into the algorithm as input.
• Encryption algorithm: The encryption algorithm alters the plaintext by performing various substitutions and transformations.
• Secret key: The encryption algorithm requires the secret key as well. The key is a value that is unaffected by the plaintext or the algorithm. Depending on whatever key is utilized at the time, the algorithm will yield a different result. The algorithm's specific substitutions and transformations are determined by the key.
- Ciphertext: The scrambled message that is generated as output. The plaintext and the secret key both play a role. Two separate keys will yield two different ciphertexts for the same message. The ciphertext is a seemingly random stream of data that is unreadable in its current state.
- Decryption algorithm: Essentially, this is the encryption algorithm reversed.
Traditional encryption must meet two requirements in order to be secure:
- A robust encryption algorithm is required. At the very least, we'd like the method to be such that an adversary who understands the algorithm and has access to one or more ciphertexts is unable to decipher the ciphertext or deduce the key. This obligation is frequently expressed in a more forceful manner: Even if the opponent has a number of ciphertexts and the plaintext that produced each ciphertext, he or she should be unable to decipher the ciphertext or uncover the key.
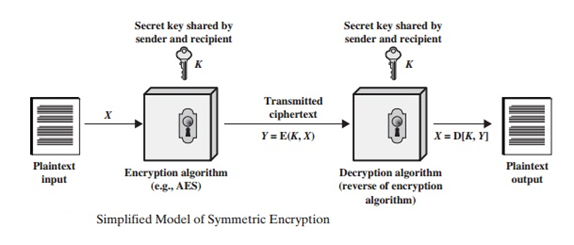
The sender and receiver must have gotten and kept copies of the secret key in a secure manner. If someone can figure out the algorithm and find the key, this key is used in all communication, and it is readable.
We presume that decrypting a message using only the ciphertext and knowledge of the encryption/decryption process is impractical. To put it another way, we simply need to keep the key secret; we don't need to keep the algorithm hidden. Symmetric encryption's ability to be widely used is due to this property.
Manufacturers can and have created low-cost chip implementations of data encryption methods because the algorithm does not need to be kept secret. These chips are widely used and can be found in a variety of goods. Maintaining the confidentiality of the key is the primary security issue with symmetric encryption.
Using Figure, let's take a deeper look at the key components of a symmetric encryption system. A source generates a plaintext message, X = [X1, X2,...., XM]. X has M elements, each of which is a letter from a finite alphabet. The alphabet used to be made up of only the 26 capital letters. The binary alphabet of 0 and 1 is commonly used nowadays. A key of the form K = [K1, K2,....., KJ] is produced for encryption. If the key is generated at the source of the communication, it must also be sent to the destination via a secure channel. A third party could also produce the key and deliver it securely to both the source and the destination.
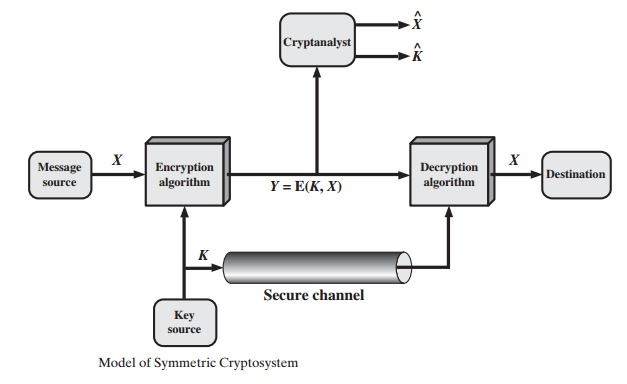
With the message X and the encryption key K as input, the encryption algorithm forms the ciphertext Y = [Y1, Y2, ..... , YN]. We can write this as
Y = E(K, X)
This notation indicates that Y is produced by using encryption algorithm E as a function of the plaintext X, with the specific function determined by the value of the key K.
The intended receiver, in possession of the key, is able to invert the transformation:
X = D (K, Y)
An opponent, observing Y but not having access to K or X, may attempt to recover X or K or both X and K. It is assumed that the opponent knows the encryption (E) and decryption (D) algorithms. If the opponent is interested in only this
Particular message, then the focus of the effort is to recover X by generating a plaintext estimate NX. Often, however, the opponent is interested in being able to read future messages as N well, in which case an attempt is made to recover K by generating an estimate K.
The substitution technique is a traditional encryption method in which the original message's characters are replaced with additional characters, integers, or symbols. If the plain text (original message) is viewed as a string of bits, the replacement approach will replace the plain text's bit pattern with the cypher text's bit pattern.
We'll go over several substitution strategies that will help us better grasp how to transform ordinary text to cypher text. We'll look at the following substitution approaches in this section:
Substitution Technique:
Caesar Cipher
Monoalphabetic Cipher
Playfair Cipher
Hill Cipher
Polyalphabetic Cipher
One-Time Pad
Cipher, Caesar
Julius Caesar devised the simplest substitution cypher. To encrypt plain text using this substitution technique, each alphabet in the plain text is substituted by the alphabet three places further away. And each alphabet in the encrypted text is replaced with the alphabet three places before it in order to decrypt it.
Let's look at an example:
Plain Text: I'll see you tomorrow
Text in Cipher: phhw ph wrpruurz
Look at the example above; we've substituted the letter 'm' with the letter 'p,' which appears three times after 'm.' Similarly, the letter ‘e' is replaced with the letter ‘h,' which appears three times following ‘e.'
Note: If the letter "z" needs to be replaced, the following three alphabets after "z" are "a," "b," and "c." So, if ‘z' appears while counting three more alphabets, it follows ‘a' in a circular pattern. This basic substitution strategy does have some disadvantages. If the hacker is aware that the Caesar cypher is in use, he just has to try 25 different keys to decrypt the plain text using brute force cryptanalysis.
The encryption and decryption algorithms are also known to the hacker.
Cipher monoalphabetic
A substitution cypher is a monoalphabetic cypher. For the whole encryption, the cypher alphabet for each plain text alphabet is fixed.
Simply put, if the plain text's alphabet 'p' is replaced with the cypher alphabet 'd'. The ciphertext will then be formed by replacing the alphabet ‘p' with the alphabet ‘d' throughout the plain text.
Cipher Playfair
A 5X5 matrix is used in the Playfair cypher, which is a substitution cypher. Let's look at how this Playfair cypher works with the help of an example:
Plain Text: I'll see you tomorrow
KEYWORD
Now we must use the provided key to convert the plain text to ciphertext. We'll go over the next steps one by one.
Step 1: Make a 5X5 matrix and fill it with the key, row by row, from left to right. Then fill in the blank space with the remaining alphabets.

Note: If a key contains duplicate alphabets, only fill those alphabets once in the matrix, and I & J should be maintained together in the matrix despite the fact that they appear in the same key.
Step 2: You must now divide the simple text into two alphabets.
Plain Text: I'll see you tomorrow
Me et me to mo rx ro wz
Note: The same letter cannot appear in two alphabets. If both letters are the same, break the pair and add a ‘x' to the previous letter. Because the letter ‘rr' occurs in pairs in our example, we split the pair and appended a ‘x' to the first ‘r'.
If the last pair has only one alphabet left after pairing, we append "z" to that alphabet to produce a pair, as in the example above. Because ‘w' was finally left alone, we added ‘z' to it.
If a pair contains the letters ‘xx,' we split it and add ‘z' to the first ‘x,' resulting in ‘xz' and ‘x_'.
3rd step: We'll convert ordinary text to ciphertext in this phase. Take the first pair of plain text and look for cypher alphabets in the matrix for the corresponding. Follow the steps below to find cypher alphabets.
Note: If both of the pair's alphabets appear in the same row, replace them with the alphabet to their right. If an alphabet from the pair appears at the extreme right, replace it with the first element of that row, so that the last element of the row in the matrix follows the first element of the same row in a circular pattern.
Replace the alphabets in the pair with the alphabet immediately below them if they occur in the same column. The last element of the column follows the first element of the same column in a circular pattern.
If the alphabets in the pair are not in the same column or row, the pair is said to be incompatible. then the alphabet is replaced by the element in its own row and the corresponding column of the other alphabet of the pair.
Me et me to mo rx ro wz
Cipher Text: kn ku kn kz ks ta kc yo
So, this is how we can convert a plain text to ciphertext using Playfair cipher. When compared with monoalphabetic cypher Playfair cypher is much more advanced. But still, it is easy to break.
Hill Cipher
Hill cypher is a polyalphabetic cypher introduced by Lester Hill in 1929. Let us discuss the technique of hill cipher.
Plain text: Binary
Key: HILL
Choose the key in such a way that it always forms a square matrix. With HILL as the key, we can form a 2×2 matrix.
Now, of plain text, you have to form a column vector of length similar to the key matrix. In our case, the key matrix is 2×2 then the column vectors of plain text would be 2×1.
The transposition technique is an encryption method that uses permutation to encode plain text. Transposition cypher is a technique for mapping plain text into cypher text using the transposition technique.
In this section, we'll look at different types of transposition techniques and how they differ from substitution techniques.
The substitution technique, on the one hand, replaces a plain text symbol with a cypher text sign. The transposition technique, on the other hand, uses permutation to generate the cypher text from plain text.
Transposition Techniques
Rail Fence Transposition
Columnar Transposition
Improved Columnar Transposition
Book Cipher/Running Key Cipher
Cipher for Rail Fence
The simplest transposition cypher is the rail fence cypher. The following are the steps to retrieve cypher text using this method:
Step 1: The plain text is typed in a diagonal pattern.
Step 2: The text is then read as a series of rows to acquire the encrypted text.
Let's look at an example to better grasp this:
Plain Text: I'll see you tomorrow,
Now, as you can see, we'll write this plain text in a diagonal format, as follows:
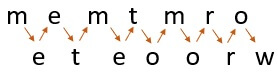
You can see why it was given the term rail fence by looking at the photograph. It resembles a rail fence.
After you've written the message as a series of diagonals, you'll need to read it as a series of rows to get the encrypted text. So, reading the first row of the rail fence, we'll obtain the first half of the cypher text:
m e m t m r o
Reading the second row of the rail fence, we'll get the second half of the cypher text:
e t e o o r w
To get the whole cypher text, join the two halves of the cypher text, and the result will be:
M E M T M R O E T E O O R W
The rail fence cypher is simple to set up and even for a cryptanalyst to decipher. As a result, a more complicated method was required.
Technique of Columnar Transposition
In comparison to the rail fence, the columnar transposition cypher is more complicated. The following are the steps to retrieve cypher text using this method:
Step 1: The plain text is written in a row-by-row pattern in the rectangular matrix of the first defined size.
Step 2: Read the text written in a rectangular matrix column by column to acquire the encryption text:
The cypher text message is the message that was obtained.
Let's look at an example to better grasp columnar transposition:
Meet plain text Tomorrow
Place the plain text in a rectangle with a predetermined size. In our case, the rectangle's predetermined size is 34. The plain text is inserted in the 34% rectangle, as shown in the image below. We've also switched the column's order around.
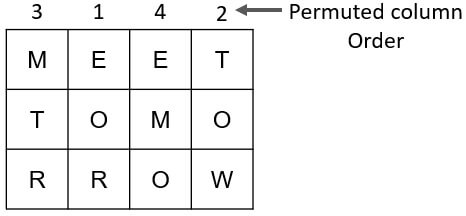
Now we must read the plain text column by column in the permuted column order to acquire the encryption text. In this case, the encrypted text obtained using the columnar transposition approach is:
MTREOREMOTOW is the cypher text.
The columnar cypher, like the rail fence cypher, is easily broken. To extract the permuted order of column and the original message, the cryptanalyst just needs to try a few permutations and combinations over the order of column. As a result, a more advanced approach was needed to reinforce the encryption.
Multiple Rounds Columnar Transposition Technique
It's similar to the basic columnar approach, but with certain improvements. The basic columnar technique is applied to the plain text several times. The following are the steps for using the columnar approach with numerous rounds:
Step 1: The plain text is written row by row in a rectangle of a given size.
Step 2: Read the plain text in the rectangle column by column to get the encryption text. Permute the order of columns as in basic columnar technique before reading the text in rectangle column by column.
Step 3: To get the final cypher text, repeat the previous steps several times.
Book Cipher or Running Key Cipher
The book cypher, also known as the running key cypher, is based on the one-time pad cypher. The key in onetime pad cypher is as lengthy as the plain text and is then deleted after usage. Each time a new key is pressed, a new message is sent.
The key or onetime pad is taken from the book in Book cypher, which is an improvement over the onetime pad. Let's go over the steps:
Step 1: Convert the plain text to numeric form using the following values: A=0, B=1, C=3,..., Z=25.
Step 2: Take a one-time pad or key from any book and convert it to numeric form as well. However, the key must be at least as long as the plain text.
Step 3: Finally, include the numeric representation of both the plain text and the key. Each plain text letter has a key text letter that corresponds to it. If the sum of any plain text letter and its associated key text letter is greater than 26, subtract 26.
Machines with rotors
Multiple steps of encryption, as seen in the preceding example, might result in an algorithm that is substantially more difficult to decrypt. This is true for both substitution and transposition cyphers. The most important application of the notion of several stages of encryption prior to the development of DES was a family of systems known as rotor machines. During World War II, both Germany (Enigma) and Japan (Purple) used machines based on the rotor principle. The Allies' success in breaking both codes was crucial to the war's conclusion.
The rotor machine's essential principle is depicted in Figure. The machine is made up of a series of independently revolving cylinders that allow electrical pulses to pass through them. Each cylinder has 26 input and output pins, with internal wiring connecting each input pin to a different output pin. Only three of each cylinder's internal connections are displayed for clarity.
Figure Three-Rotor Machine with Wiring Represented by Numbered Contacts
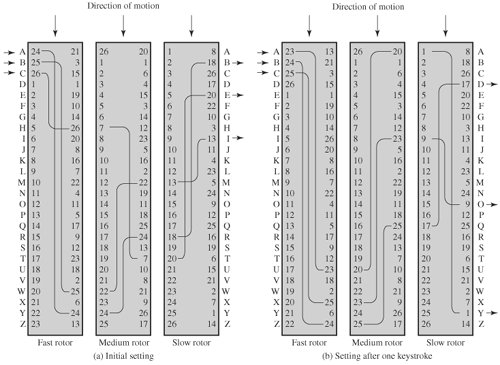
If each input and output pin is assigned to a letter of the alphabet, a monoalphabetic substitution is defined by a single cylinder. In Figure, an electric signal is applied to the first pin of the first cylinder and flows through the internal connection to the twenty-fifth output pin when an operator depresses the letter A key.
Consider a machine that just has one cylinder. The cylinder rotates one position after each input key is depressed, shifting the internal connections appropriately. As a result, a new monoalphabetic substitution cypher is created. The cylinder would return to its original location after 26 letters of plaintext.
As a result, we have a 26-period polyalphabetic substitution method.
A single-cylinder system is simple and does not provide a significant cryptanalytic challenge. The rotor machine's power comes from the usage of many cylinders, with one cylinder's output pins connected to the input pins of the next. A three-cylinder arrangement is depicted in Figure. The input from the operator to the first pin is routed through the three cylinders and appears at the output of the second pin in the left part of the picture.
Each keystroke spins one pin position in the cylinder nearest to the operator input. The middle cylinder rotates one pin position for every complete revolution of the inner cylinder. Finally, the outer cylinder rotates one pin position for every complete revolution of the central cylinder. This is the same procedure that an odometer performs. As a result, before the system repeats, there are 26 x 26 x 26 = 17,576 possible substitution alphabets used. When the fourth and fifth rotors are added, the periods increase to 456,976 and 11,881,376 letters, respectively. When it comes to a five-rotor machine, David Kahn put it succinctly [KAHN96, page 413]: "For every complete rotation of the inner cylinder, the middle cylinder rotates one pin position." This is the same procedure that an odometer performs. As a result, before the system repeats, there are 26 x 26 x 26 = 17,576 possible substitution alphabets used. When the fourth and fifth rotors are added, the periods increase to 456,976 and 11,881,376 letters, respectively. In his brilliant description of a five-rotor machine [KAHN96, page 413], David Kahn said:
Steganography is the use of a variety of techniques to conceal information from prying eyes. Steganography was largely done physically in ancient times.
The earliest known incidence of steganography originates from 500 BC, when Histiaeus, the monarch of Miletus, tattooed a message on the shaved head of one of his slaves and then allowed the hair to regrow. He then handed the slave over to his son-in-law, Aristagoras, who shaved the slave's head once more and disclosed the message.
More advanced kinds of steganography, such as invisible inks, were developed in the centuries that followed. Steganography has now made its way into the digital realm.
“By definition, steganography is the concealment of one file within another,” says Ira Winkler. Trustwave's lead security principal.
What is steganography and how does it work?
Steganography works by concealing information in a non-suspicious manner. Least significant bit (LSB) steganography is one of the most prevalent methods. The information hider embeds the hidden information in the least significant bits of a media file in this style of steganography.
In an image file, for example, each pixel contains three bytes of data corresponding to the hues red, green, and blue (some image formats add a fourth byte for transparency, or ‘alpha').
LSB steganography hides one piece of data by changing the final bit of each of those bytes. So, if you want to hide one megabyte of data with this method.
You'll need a picture file that's eight megabytes in size.
A person seeing the original and the steganographically modified photographs will not be able to detect the difference since altering the last bit of the pixel value does not result in a visually noticeable change to the picture.
The practice of hiding one file inside another is known as steganography.
Other digital media (audio and video) can use the similar method, with data buried in areas of the file that cause the least amount of change to the auditory or visual output.

Steganography is the practice of hiding of one file within another
The use of word or letter substitution is a less well-known steganography technique.
The sender of the secret message conceals the text by inserting the words at certain intervals throughout a much larger text.
While this strategy is simple to employ, it may cause the text to appear weird and out of place because the secret words may not fit well into their target sentences.
Other methods of steganography include concealing a hard drive partition or embedding data in the header section of files and network packets. The effectiveness of these methods is determined by the amount of data they can conceal and the ease with which they can be detected.
References:
1. “Cryptography and Network Security: Principles and Practice” by William Stallings
2. “A Course in Number Theory and Cryptography” by Neal Koblitz.
3. “Cryptography Theory and Practice” by Doug Stinson
4. Modern Cryptography, Probabilistic Proofs and Pseudorandomness, Oded Goldreich, Springer-Verlag 1998