Unit - 4

Encryption standard and ciphers

4.1 Encryption standard and ciphers

Because the Data Encryption Standard (DES) has been discovered to be vulnerable to extremely powerful attacks, its popularity has been on the wane.

DES is a block cypher that encrypts data in 64-bit blocks. This implies that 64 bits of plain text are fed into DES, which generates 64 bits of encrypted text. Encryption and decryption employ the same algorithm and key, with slight variations. The key is 56 bits long. The essential concept is depicted in the diagram.

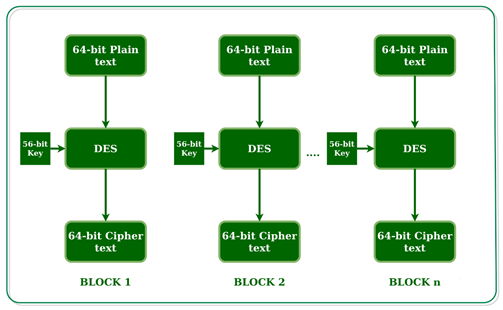
DES employs a 56-bit key, as previously stated. The initial key is actually 64 bits long. However, every eighth bit of the key is destroyed before the DES process even begins, resulting in a 56-bit key. Bit positions 8, 16, 24, 32, 40, 48, 56, and 64 are all eliminated in this way.

Fig. Discording of every 8th bit of original key

As a result, deleting every 8th bit of the key yields a 56-bit key from a 64-bit key.

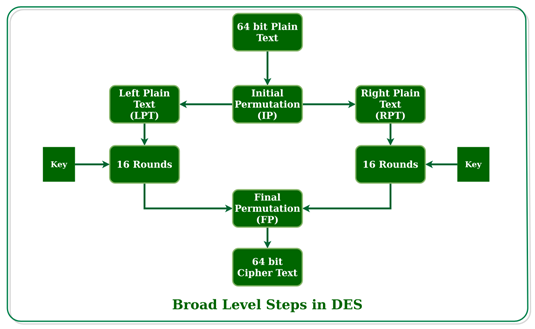
The substitution and transposition properties of cryptography are the foundations of DES (also called as diffusion). DES has 16 steps, each of which is referred to as a round. Substitution and transposition are performed in each round. Let's talk about the high-level steps in DES presently.

• The 64-bit plain text block is given over to an initial Permutation (IP) function in the first stage.
• The first permutation was carried out on plain text.
• Following that, the initial permutation (IP) creates two halves of the permuted block, referred to as Left Plain Text (LPT) and Right Plain Text (RPT) (RPT)
• Each LPT and RPT must now undergo a 16-round encryption process.
• Finally, LPT and RPT are reconnected, and the combined block is subjected to a Final Permutation (FP).
• As a result of this procedure, 64-bit encrypted text is generated.

Initial Permutation (IP) - As previously stated, the Initial Permutation (IP) occurs just once, before the first round. As seen in the diagram, it advises how the IP transposition should continue.

It says, for example, that the IP replaces the first bit of the original plain text block with the 58th bit, the second bit with the 50th bit of the original plain text block, and so on.

This is nothing more than a jigsaw puzzle of bit locations from the plain text block. The same rule holds true for all of the other bit places shown in the diagram.

Fig. Initial permutation table

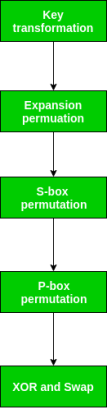
The resulting 64-bit permuted text block is separated into two half blocks, as we saw following IP. Each half block is made up of 32 bits, and each of the 16 rounds is made up of the broad level steps shown in the diagram.

4.2 Evaluation criteria for AES

Over a longer length of time, AES has been subjected to more scrutiny than any other encryption algorithm, and no successful cryptanalytic attack based on the algorithm rather than brute force has been discovered. As a result, there is a high amount of confidence that 3DES is cryptanalysis resistant. If only security was a factor, 3DES would be an excellent choice for a standardized encryption algorithm for many years to come.

The main disadvantage of 3DES is that it is a relatively slow algorithm in software. The original DES was created for hardware implementation in the mid-1970s, and therefore does not produce efficient software code. 3DES has three times the number of rounds as DES.

Is, as a result, slower. Another disadvantage is that DES and 3DES both employ a 64-bit block size. A higher block size is beneficial for both efficiency and security reasons.

3DES is not a good option for long-term use because of these flaws. In 1997, the National Institute of Standards and Technology (NIST) released a request for suggestions for a new Advanced Encryption Standard (AES), which should have security strength equivalent to or greater than 3DES and greatly improved efficiency. 15 suggested methods were accepted in the first round of evaluation. After a second round, the field was reduced to five algorithms. In November 2001, NIST finished its evaluation process and issued a final standard (FIPS PUB 197).

Rijndael was chosen by NIST as the suggested AES algorithm. Dr. Joan Daemen and Dr. Vincent Rijmen are both cryptographers from Belgium who designed and submitted Rijndael for the AES.

AES is intended to eventually replace 3DES, but this will take several years. 3DES is expected to remain an approved algorithm (for use by the US government) for the foreseeable future, according to NIST.

NIST Criterion for Evaluating Possible Applicants-worth It's looking into NIST's criteria for evaluating potential candidates. These requirements cover a wide variety of issues related to the practical use of current symmetric block cyphers. In reality, two different sets of criteria emerged. In 1997, NIST asked for candidate algorithm suggestions for the first time. The following were the three types of criteria:

The effort required to cryptanalyze an algorithm is referred to as security. The focus of the evaluation was on the attack's practicality. Because the minimal key size for AES is 128 bits, brute-force assaults were deemed impracticable with existing and predicted technologies.

As a result, the emphasis in this case is on cryptanalysis rather than a brute-force approach.

AES is expected to be cost-effective in a wide range of applications, according to NIST. As a result, AES must be computationally efficient in order to be used in high-speed applications like broadband networks.

Characteristics of the algorithm and its implementation:

This category comprises a number of factors, such as flexibility, adaptability for a wide range of hardware and software implementations, and simplicity, which makes security analysis easier.

4.3 Advanced Encryption Standard Cipher

The Advanced Encryption Standard (AES) is the most popular and commonly used symmetric encryption algorithm available today (AES). It is at least six times faster than triple DES in terms of discovery.

Because the key size of DES was too small, a replacement was required. It was thought to be vulnerable to an exhaustive key search assault as processing power increased. Triple DES was created to address this flaw, however it was proven to be sluggish.

The following are the characteristics of AES:

• Symmetric block cypher with symmetric key
• Data in 128 bits, keys in 128/192/256 bits
• Triple-DES is stronger and faster.
• Specifications and design specifications should be provided in full.
• Software written in C and Java.

AES's operation

Rather than being a Feistel cypher, AES is an iterative cypher. It is built on the basis of a ‘substitution–permutation network.' It consists of a sequence of connected processes, some of which require substituting specified outputs for inputs (substitutions) and others involving shuffling bits around (permutations).

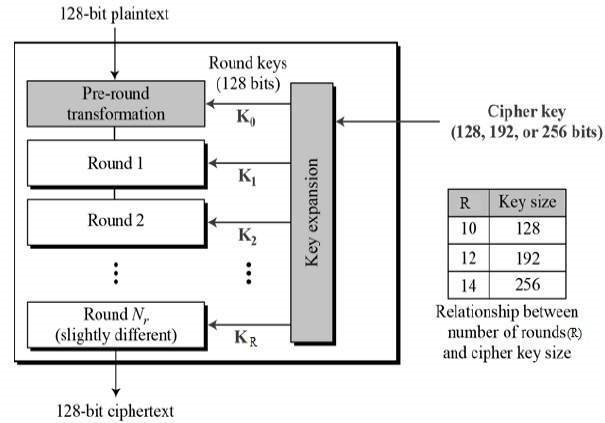
Surprisingly, AES uses bytes rather than bits for all of its calculations. As a result, AES considers a plaintext block's 128 bits as 16 bytes. For matrix processing, these 16 bytes are organized into four columns and four rows. In contrast to DES, the number of rounds in AES is configurable and dependent on the key length. For 128-bit keys, AES employs 10 rounds, 12 rounds for 192-bit keys, and 14 rounds for 256-bit keys.

Each of these rounds use a unique 128-bit round key derived from the original AES key.

The AES structure is depicted schematically in the diagram below.

Process of Encryption

We'll stick to describing a typical cycle of AES encryption here. There are four sub-processes in each round. The first round is illustrated in the diagram below.

Substitution of Bytes (Sub Bytes)

By looking up a fixed table (S-box) provided in design, the 16 input bytes are substituted. The end result is a four-row, four-column matrix.

Shift rows

Each of the matrix's four rows is shifted to the left. Any entries that fall off the right side of the row are re-inserted. The following is how the shift is carried out:

• The first row has not been shifted.
• The second row has been moved one (byte) to the left.
• The third row has been moved two spaces to the left.
• The fourth row has been moved three positions to the left.
• The outcome is a new matrix made up of the same 16 bytes that have been shifted in relation to each other.

Mix Columns

A particular mathematical function is now used to alter each column of four bytes. This function takes four bytes from one column as input and returns four entirely new bytes that replace the original column. As a result, a new matrix with 16 additional bytes is created. It's worth noting that this stage is skipped in the final round.

Add round key

The matrix's 16 bytes are now treated as 128 bits, and they are XORed with the round key's 128 bits. The ciphertext is the output if this is the final round.

Process of Decryption

The reverse process of decrypting an AES ciphertext is analogous to the reverse process of encryption. Each round consists of four processes that are performed in reverse order.

• Include a circular key.
• Columns should be mixed.
• Rows are shifted.
• Substitution of bytes

Because the sub-processes in each round are reversed, unlike a Feistel Cipher, the encryption and decryption algorithms must be implemented separately, despite their close relationship.

AES Evaluation

AES is widely used and supported in both hardware and software in today's encryption. There have been no practical cryptanalytic attacks against AES discovered too far. Furthermore, AES has built-in key length flexibility, which provides some ‘future-proofing' against advancements in the capacity to do exhaustive key searches.

However, AES security is only guaranteed if it is appropriately implemented and good key management is used, just as it is with DES.

4.4 Multiple encryption and Triple DES

Numerous encryption is a technique that employs the usage of the same encryption algorithm multiple times. The encryption algorithm is used to transform plaintext to ciphertext in the first place. Triple DES employs three stages of the DES algorithm, with two or three different keys in total.

Given the possibility of DES being vulnerable to a brute-force assault, there has been a lot of interest in finding a replacement. One option is to create a whole new algorithm, such as AES, which is a good example. Another option is to utilize multiple encryption with DES and multiple keys, which would preserve existing software and equipment investments. We'll start with the most basic example of this second option. After that, we'll look at the widely used triple DES (3DES) method.

DES (Double DES)

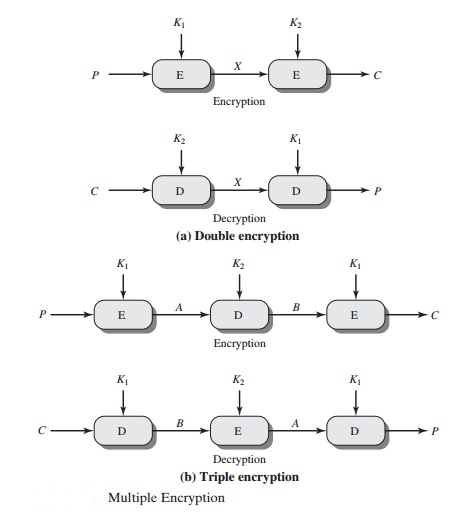
Multiple encryption in its most basic form comprises two encryption stages and two keys (Figure. The ciphertext C is created using a plaintext P and two encryption keys K1 and K2.

C = E (K2, E (K1, P))

Decryption necessitates applying the keys in reverse order:

P = D (K1, D (K2, C))

This approach appears to use a key length of 56 * 2 = 112 bits for DES, resulting in a significant boost in cryptographic strength. However, we must investigate the algorithm further.

A SINGLE STAGE REDUCTION Assume that for all 56-bit key values in DES, finding a key K3 such that E (K2, E (K1, P)) = E (K3, P)   

If this is the case, then double encryption, and indeed any number of steps of multiple encryption using DES, is pointless because the outcome is equivalent to a single encryption with a single 56-bit key.

On the surface, Equation does not appear to be likely to hold. Take into account that DES encryption is a mapping of 64-bit blocks to 64-bit blocks. The mapping can actually be considered as a permutation. That is, if all 264 possible input blocks are considered,

Decryption to recover the original plaintext would be impossible if, for example, two given input blocks mapped to the same output block. How many alternative mappings are there that yield a permutation of the input blocks with 264 potential inputs? The worth is readily apparent.

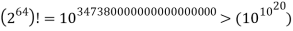
DES, on the other hand, creates one mapping for each unique key, for a total of 256 mappings:

256 6 1017

As a result, it's plausible to infer that if DES is applied twice with different keys, one of the numerous mappings that aren't determined by a single application of DES will result. Despite the fact that there was a lot of evidence to back up this claim, it wasn't verified until 1992.

ATTACK IN THE MIDDLE (MEET-IN-THE-MIDDLE) As a result, double DES encryption produces a mapping that is not equal to single DES encryption. However, there is a way to attack this scheme that does not rely on any specific feature of DES and may be used against any block encryption cypher.

[DIFF77] was the first to explain the algorithm, which is known as a meet-in-the-middle attack. It is founded on the premise that if we have

Then (see above figure a)

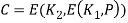
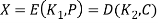
The assault is carried out as follows, given a known pair (P, C). To begin, encrypt P for each of the 256 possible K1 values. Put the findings in a table, and then sort the table by X values. Then, using all 256 potential K2 values, decode C. Check the outcome of each decryption against the table to see if it matches. If a match is found, compare the two keys to a previously known plaintext–ciphertext pair. Accept the two keys as the correct keys if they create the correct ciphertext.

DES Triple with Two Keys

The use of three layers of encryption with three separate keys is an obvious defence to the meet-in-the-middle attack. The cost of a meet-in-the-middle attack rises to 2112, which is well above what is feasible now and in the future. It does, however, have the disadvantage of requiring a key length of 56 * 3 = 168 bits, which can be cumbersome.

Tuchman developed a triple encryption scheme that employs only two keys as an alternative [TUCH79]. An encrypt-decrypt-encrypt (EDE) sequence is followed by the function.

C = E (K1, D (K2, E (K1, P)))

P = D (K1, E (K2, D (K1, C)))

The usage of decryption for the second stage has no cryptographic importance. Its only benefit is that it allows 3DES users to decrypt data encrypted by older single DES users:

C = E (K1, D (K1, E (K1, P))) = E (K1, P)

P = D (K1, E (K1, D (K1, C))) = D (K1, C)

3DES with two keys is a popular variation to DES that has been included in the key management standards ANS X9.17 and ISO 8732.1.

There are currently no feasible cryptanalytic attacks against 3DES. Coppersmith [COPP94] estimates that the cost of a brute-force key search on 3DES is on the order of 2112 L (5 * 1033) and that the cost of differential cryptanalysis is exponentially increasing, nearing 1052, when compared to single DES.

It's worth taking a look at a few proposed 3DES assaults that, while not practical, give you an idea of the types of attacks that have been investigated and could be the foundation for more effective future attacks. Merkle and Hellman [MERK81] made the first serious suggestion. Their strategy entails locating plaintext values that result in an initial intermediate value of A = 0.

Three-key DES (Triple DES)

Although the attacks detailed above appear to be impracticable, anyone who uses two-key 3DES should be concerned. As a result, many researchers now believe that three-key 3DES is the best option (e.g., [KALI96a]). The three-key 3DES algorithm is specified as C = E (K3, D (K2, E (K1, P)) and has an effective key length of 168 bits.

By setting K3 = K2 or K1 = K2, backward compatibility with DES is ensured.

4.5 Block Cipher modes of Operation

Encryption techniques are classified as block cyphers or stream cyphers based on the kind of input. A block cypher is an encryption technique that accepts a given size input, such as b bits, and generates a ciphertext of the same size. It is possible to divide the input further if it is larger than b bits. A block cypher can operate in a variety of ways depending on the application and purpose.

Electronic Code Book (ECB) - The simplest block cypher mode of operation is the electronic code book. It is simpler since each block of input plaintext is directly encrypted, and the output is in the form of encrypted ciphertext blocks. If a message is larger than b bits in size, it is usually ignored. It can be dismantled into a series of blocks, and the procedure repeated.

The ECB's procedure is as follows:

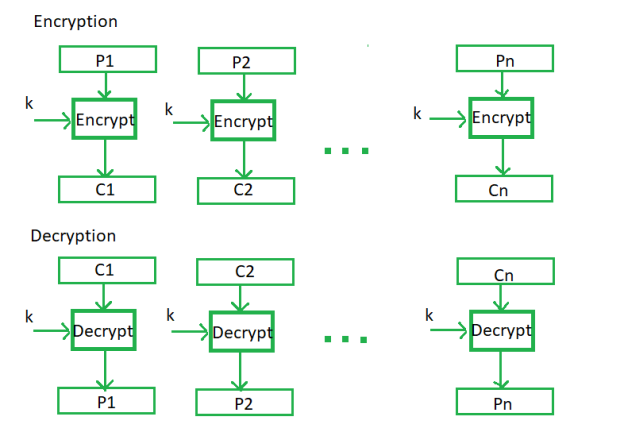
Advantages of utilizing ECB –

• It is possible to encrypt blocks of bits in parallel, making it a faster method of encryption.
• Block cypher in a simple manner.

Disadvantages of utilizing ECB –

• Prone to cryptanalysis because plaintext and ciphertext have a direct link.

Cipher Block Chaining (CBC) –

Since ECB breaches some security standards, CBC is an upgrade made on ECB. After XOR with the original plaintext block, the preceding cypher block is sent as input to the next encryption method in CBC. In a nutshell, a cypher block is created by encrypting the XOR output of the previous cypher block and the plaintext block now being used.

The following diagram depicts the procedure:

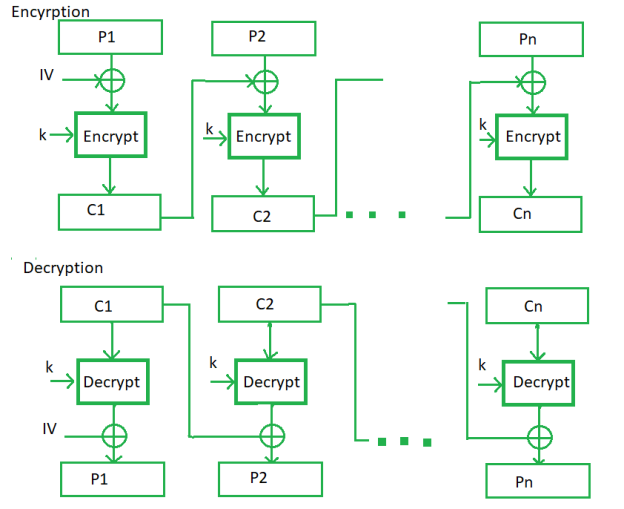
Advantages of CBC –

• For input greater than b bits, CBC works well.
• CBC is a reliable authentication method.
• ECB has a more resistant character to cryptanalysis.

Disadvantages of CBC –

• Because each encryption requires a preceding cypher, parallel encryption is not possible.

CFB (Cipher Feedback Mode) –

The cypher is delivered as feedback to the following block of encryption in this mode, with some new specifications: the first encryption is done with an initial vector IV, and the output bits are separated into a set of sand b-s bits. The left-hand sbits are selected and an XOR operation with plaintext bits is performed.

The result is fed into a shift register, and the cycle repeats. Both the encryption and decryption processes for the same are shown below, and they both use the encryption algorithm.

4.6 Stream cipher and RCG

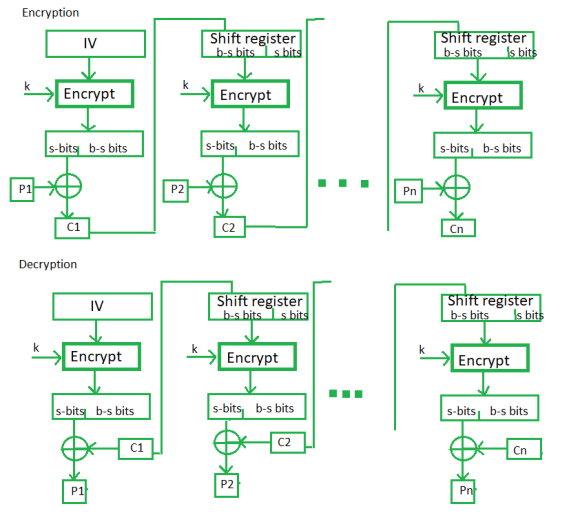
Stream cyphers are encryption algorithms that handle bits, bytes, or characters of plaintext one at a time. In terms of hardware, stream cyphers are frequently faster than block cyphers and require less sophisticated circuitry. Because they have minimal or no error propagation, they are also beneficial when transmission problems are expected to occur.

There are three types of stream cyphers: synchronous, self-synchronizing, and one-time pad. A keystream is created independently from the plaintext and ciphertext in synchronous cyphers. To successfully decode the data, they must be in the same condition and use the same key. If a character in the ciphertext is changed, it has no effect on the rest of the ciphertext's decryption; however, if a character is deleted or inserted, synchronization is broken, and the rest of the decryption fails. A keystream is formed from the key and a defined number of prior ciphertext characters in self-synchronizing (asynchronous) cyphers. Because the state only depends on the set number of prior ciphertext characters, this sort of stream cypher can better withstand characters being deleted or inserted. The cypher will be synced once that number has been processed. A synchronous stream cypher has no error propagation, but a self-synchronizing cypher has some. If a character is changed, the maximum number of faulty decryptions is restricted to the previous ciphertext characters given, after which accurate decryption resumes.

Stream cyphers are ideal for quick implementations that use little resources. These two aspects assist the defender in implementing resistance techniques on devices that lack the resources to install a block cypher. Wireless signals, which are more naturally suited to a streaming paradigm than data transmitted in bigger, fixed-size chunks, can also benefit from stream cyphers. GSM phones, for example, employ the A5/1 stream cypher [19], while security systems for wireless local area networks (WLANs) use the RC4 stream cypher [20]. Stream cyphers' simplicity is both a benefit and a drawback. It appears that properly incorporating stream cyphers into cryptosystems. Is more complex.

Even though the RC4 cypher was not broken—it was just designed badly—the implementation of RC4 in Wired Equivalent Privacy (WEP) for WLAN security was a disaster [20]. The implementation, in particular, artificially shortened the critical period; the technical reason for this is described shortly.

Stream cyphers are divided into two types: those that operate best in hardware and those that work best in software. A5/1 is an example of a hardware-friendly encryption. It belongs to the linear feedback shift registers (LFSRs) family of algorithms, which are simple to build with a little electrical engineering understanding.

RC4 is an example of a software-friendly cypher that is optimized for low resource utilization. Simple array-based operations and less than 1 kilobyte of RAM are all that's required.

Stream cyphers are similar to block cyphers in that they utilize conceptual tools. The major tool is substitution, which involves combining each bit or byte of plaintext with the key material using an exclusive-or (XOR) operation to turn the plaintext bit into the ciphertext bit. Binary XOR is a straightforward operation. There are just two potential values: 1 or 0, and the outcome is 0 if the two inputs are the same, else it is 1.

References:

1. “Cryptography and Network Security: Principles and Practice” by William Stallings

2. “A Course in Number Theory and Cryptography” by Neal Koblitz.

3. “Cryptography Theory and Practice” by Doug Stinson

4. Modern Cryptography, Probabilistic Proofs and Pseudorandomness, Oded Goldreich, Springer-Verlag 1998