Unit 1
Magnetic fields and magnetic circuits
The MMF is defined as the work done in moving the unit magnetic pole (1weber) once around the magnetic circuit.
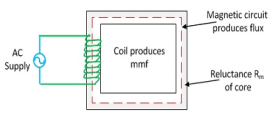
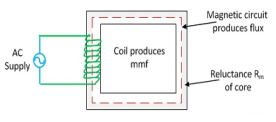
The magnetomotive force (MMF) is required to drive the magnetic flux in the magnetic circuit. The magnetic pressure, which sets up the magnetic flux in the circuit as called Magnetomotive Force. The SI unit of MMF is Ampere-turn (AT), and their CGS unit is G (gilbert). The MMF for the inductive coil shown in the figure below is expressed as
F=NI
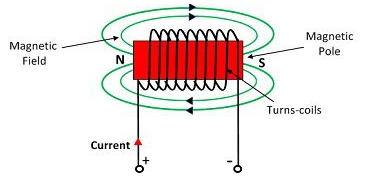
The strength of the MMF is equivalent to the product of the current around the turns and the number of turns of the coil.
Magnetic Flux:
The number of magnetic lines of forces set up in a magnetic circuit is called Magnetic Flux. It is analogous to electric current, I in an electric circuit. Its SI unit is Weber (Wb) and its CGS unit is Maxwell. It is denoted by φB.
ΦB=B.S
ΦB=B.S Cos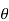
B – the magnitude of the magnetic field
S – area of surface
θ – angle between the magnetic field lines and perpendicular distance normal to the surface area
Magnetic flux for a closed surface
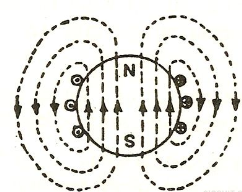
ΦB=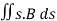
=0
Magnetic flux for open surface is
E=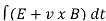
E=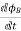
E – electromotive force
v – velocity of the boundary
E – electric field
B – magnetic field
øB - magnetic flux through the open surface
The magnetic flux through a closed surface is always zero, but in the open surface, it is not zero.
Magnetic Reluctance:
The obstruction offered by a magnetic circuit to the magnetic flux is known as reluctance.
S=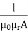
l – the length of the conductor
μo – permeability of vacuum which is equal to 4π Χ10-7 Henry/metre.
μr – relative permeability of the material.
A – cross-section area of the conductor.
Its SI unit is AT / Wb (ampere-turns / Weber)
Magnetic Inductance
The ability of an inductor to store energy in the form of magnetic field(and consequently to oppose the change in current)is called inductance. It is measured in the units of Henry(H).
Que) A laminated soft iron ring of relative permeability 800 has a mean circumference of 600mm and a cross sectional area of 400mm2. A radial air gap of 1mm width is cut in the ring which is wound with 800 turns. Calculate the current required to produce an air gap flux of 0.5mWb if leakage factor is 1.2 and stacking factor 0.9.
Sol: Required Ampere turn = 
gSg+ 
iSi
=
+ 
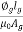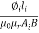
Air gap flux 
s=0.5mWb
lg=1mm=1x10-3m
Ag=400mm2=400x10-6
Flux in iron ring 
i=1.2x0.5x10-3=0.6mWb
Net cross-sectional area = Ai x stacking factor=400x10-6 x 0.9=360x10-6
Total AT required=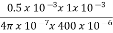
+ 
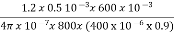= 994.72
I=A/N=994.72/800=1.24A
Que) An iron ring has X-section of 4cm2 and a mean diameter of 25cm. An air-gap of 0.3mm has been cut across the section of the ring. The ring is wound with a coil of 220 turns through which a current of 2A is passed. If the total magnetic flux is 0.24mWb, find relative permeability of iron?
Sol: φ=0.24mWb
A=4cm2=4 x 10-4
B= φ/A=0.24 x 10-3/4 x 10-4=0.6Wb/m2
AT for iron ring=H x l=(B/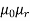
)/l=(0.6/
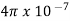x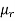
) x 0.25=1.19 x 105/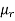
AT for air gap= H x l=( B/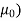
/l=(0.6/
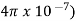x 0.3x10-3=143.24
Total AT required=(1.19 x 105/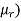
+143.24
Total AT provided=220 x 2=440
Therefore,
(1.19 x 105/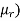
+143.24=440
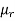= 400.99
The law states that the mmf around a closed path is equal to the current enclosed by the path. The law cab be studied for
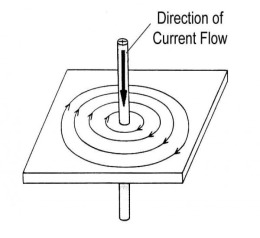
a) MMF around long straight conductor:
Let the conductor carry current of I amperes. The magnetic field consists of circular line of forces having their plane perpendicular to the conductor. If a unit pole is place at radius r, than work done to move the pole once round the conductor against this force is
Mmf= force x distance= I
I= H x 2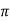
r
H=I/2
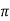r
For N conductors
H=NI/2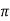
r (A/m)
B= μoH
B= μo NI/2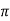
r (Wb/m2 or tesla)
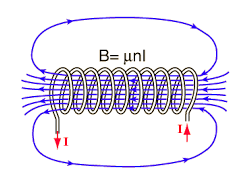
b) Magnetic field strength of long solenoid:
The magnetic field along the solenoid is H. The ampere turns linked with the path are NI. Then according to Ampere’s Law
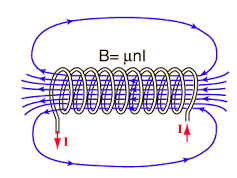
H x l=NI
H=NI/l (A/m)
B= μoH
B=μoNI/l (Wb/m2 or tesla)
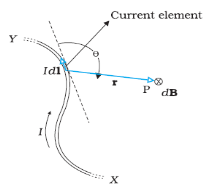
Boit-Savart Law:
The expression for the magnetic field strength dH produced at point P for small length dl of a conductor carrying current of I amperes is given as
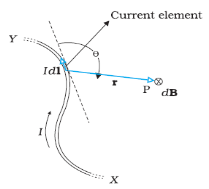
DH=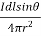
A/m
DB0= μo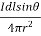 
Wb/m2
Que) Calculate the magnetising force and flux density at a distance of 4cm from a long straight circular conductor carrying a current of 250A and placed in air?
Sol: H=I/2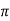
r
=250/2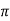
x 0.04=994.71 AT/m
B= μoH
=4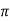
x10-7x994.71=1.25x10-3 Wb/m2
Que) A wire 2.5m long is bent into a square and into a circle. If the current flowing through the wire is 100 A, find the magnetising force at the centre of the square and the centre of the circle?
Sol: Value of h at centre of square will be H=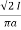
= 
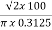=144 AT/m
Value of H at the centre of circle is H=I/2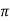
r
=125.6AT/m
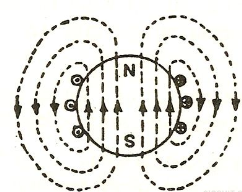
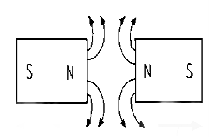
Bar Magnet:
All magnets have two regions called magnetic poles with the magnetism both in and around a magnetic circuit producing a definite chain of organised and balanced pattern of invisible lines of flux around it. These lines of flux are called as the magnetic field of the magnet. At each end of a magnet is a pole. Magnetic poles are always present in pairs, there is always a region of the magnet called the North-pole and there is always an opposite region called the South-pole. The lines which go to make up a magnetic field showing the direction and intensity are called Lines of Force or Magnetic Flux and represented as Phi ( Φ ).
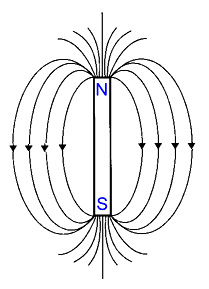
- Lines of force never cross.
- Lines of force are continuous.
- Lines of force always form individual closed loops around the magnet.
- Lines of force have a definite direction from North to South.
- Lines of force that are close together indicate a strong magnetic field.
- Lines of force that are farther apart indicate a weak magnetic field.
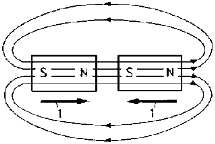
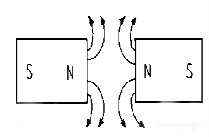
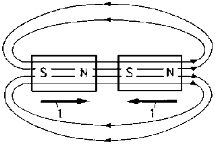
Like poles of the magnet repel each other and unlike poles attract each other.
Magnetic flux density =Magnet flux/Area
B=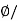
A Tesla
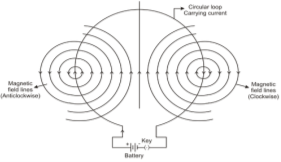
Current carrying coil:
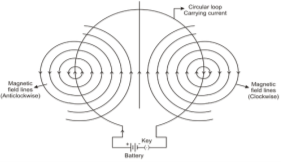
The magnetic field lines are concentric circles at every point of a current carrying circular loop. The direction of magnetic field of every section of the circular loop can be found by using the right-hand thumb rule.
- At the centre of the circular loop, magnetic field lines are straight.
- Each segment of circular loop carrying current produces magnetic field lines in the same direction with in the loop.
- The direction of magnetic field at the centre of circular coil is perpendicular to the place of the coil. i.e. along the axis of the coil.
Factors affecting the strength of magnetic field
- The magnitude of magnetic field is directly proportional to the magnitude of current through the loop. i.e. B∝I.
- The magnitude of magnetic field is inversely proportional to the radius of the circular loop. i.e. B∝1/r.
Que) The amount of flux present in around magnetic bar was measured at 0.013 weber. If the material has a diameter of 14cm, calculate the flux density.
Sol: Area=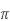
r2
Diameter=2r
r=14/2=7cm=0.07m
Area=3.14 x 0.072=0.0154m2
Flux Density B==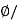
A=0.013/0.0154=0.843 Tesla
Que) Calculate the radius of the material having flux density of 0.5 T and flux present around the magnetic bar is 0.02T.
Sol: Flux Density B=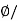
A
A=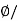 
B=0.02/0.5=0.04 m2
Area=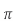
r2
r=0.113m
A highly permeable substance like ferromagnetic materials allow the magnetic lines of forces to pass through them easily. When a ferromagnetic material is placed in the magnetic field the magnetic lines of forces are concentrated inside the substance.
Unit 1
Magnetic fields and magnetic circuits
The MMF is defined as the work done in moving the unit magnetic pole (1weber) once around the magnetic circuit.
The magnetomotive force (MMF) is required to drive the magnetic flux in the magnetic circuit. The magnetic pressure, which sets up the magnetic flux in the circuit as called Magnetomotive Force. The SI unit of MMF is Ampere-turn (AT), and their CGS unit is G (gilbert). The MMF for the inductive coil shown in the figure below is expressed as
F=NI
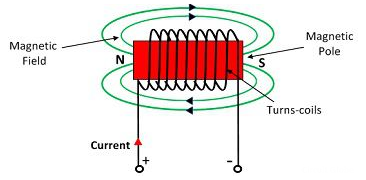
The strength of the MMF is equivalent to the product of the current around the turns and the number of turns of the coil.
Magnetic Flux:
The number of magnetic lines of forces set up in a magnetic circuit is called Magnetic Flux. It is analogous to electric current, I in an electric circuit. Its SI unit is Weber (Wb) and its CGS unit is Maxwell. It is denoted by φB.
ΦB=B.S
ΦB=B.S Cos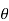
B – the magnitude of the magnetic field
S – area of surface
θ – angle between the magnetic field lines and perpendicular distance normal to the surface area
Magnetic flux for a closed surface
ΦB=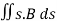
=0
Magnetic flux for open surface is
E=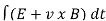
E=
E – electromotive force
v – velocity of the boundary
E – electric field
B – magnetic field
øB - magnetic flux through the open surface
The magnetic flux through a closed surface is always zero, but in the open surface, it is not zero.
Magnetic Reluctance:
The obstruction offered by a magnetic circuit to the magnetic flux is known as reluctance.
S=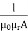
l – the length of the conductor
μo – permeability of vacuum which is equal to 4π Χ10-7 Henry/metre.
μr – relative permeability of the material.
A – cross-section area of the conductor.
Its SI unit is AT / Wb (ampere-turns / Weber)
Magnetic Inductance
The ability of an inductor to store energy in the form of magnetic field(and consequently to oppose the change in current)is called inductance. It is measured in the units of Henry(H).
Que) A laminated soft iron ring of relative permeability 800 has a mean circumference of 600mm and a cross sectional area of 400mm2. A radial air gap of 1mm width is cut in the ring which is wound with 800 turns. Calculate the current required to produce an air gap flux of 0.5mWb if leakage factor is 1.2 and stacking factor 0.9.
Sol: Required Ampere turn =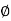 
gSg+ 
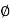iSi
=
+ 
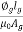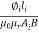
Air gap flux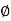 
s=0.5mWb
lg=1mm=1x10-3m
Ag=400mm2=400x10-6
Flux in iron ring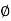 
i=1.2x0.5x10-3=0.6mWb
Net cross-sectional area = Ai x stacking factor=400x10-6 x 0.9=360x10-6
Total AT required=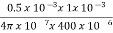
+ 
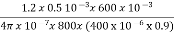= 994.72
I=A/N=994.72/800=1.24A
Que) An iron ring has X-section of 4cm2 and a mean diameter of 25cm. An air-gap of 0.3mm has been cut across the section of the ring. The ring is wound with a coil of 220 turns through which a current of 2A is passed. If the total magnetic flux is 0.24mWb, find relative permeability of iron?
Sol: φ=0.24mWb
A=4cm2=4 x 10-4
B= φ/A=0.24 x 10-3/4 x 10-4=0.6Wb/m2
AT for iron ring=H x l=(B/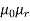
)/l=(0.6/
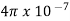x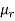
) x 0.25=1.19 x 105/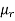
AT for air gap= H x l=( B/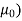
/l=(0.6/
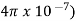x 0.3x10-3=143.24
Total AT required=(1.19 x 105/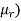
+143.24
Total AT provided=220 x 2=440
Therefore,
(1.19 x 105/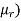
+143.24=440
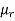= 400.99
The law states that the mmf around a closed path is equal to the current enclosed by the path. The law cab be studied for
a) MMF around long straight conductor:
Let the conductor carry current of I amperes. The magnetic field consists of circular line of forces having their plane perpendicular to the conductor. If a unit pole is place at radius r, than work done to move the pole once round the conductor against this force is
Mmf= force x distance= I
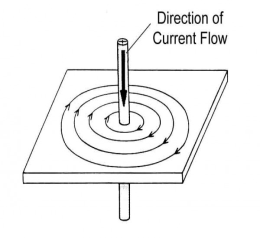
I= H x 2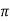
r
H=I/2
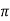r
For N conductors
H=NI/2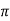
r (A/m)
B= μoH
B= μo NI/2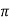
r (Wb/m2 or tesla)
b) Magnetic field strength of long solenoid:
The magnetic field along the solenoid is H. The ampere turns linked with the path are NI. Then according to Ampere’s Law
H x l=NI
H=NI/l (A/m)
B= μoH
B=μoNI/l (Wb/m2 or tesla)
Boit-Savart Law:
The expression for the magnetic field strength dH produced at point P for small length dl of a conductor carrying current of I amperes is given as
DH=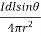
A/m
DB0= μo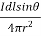 
Wb/m2
Que) Calculate the magnetising force and flux density at a distance of 4cm from a long straight circular conductor carrying a current of 250A and placed in air?
Sol: H=I/2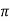
r
=250/2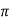
x 0.04=994.71 AT/m
B= μoH
=4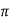
x10-7x994.71=1.25x10-3 Wb/m2
Que) A wire 2.5m long is bent into a square and into a circle. If the current flowing through the wire is 100 A, find the magnetising force at the centre of the square and the centre of the circle?
Sol: Value of h at centre of square will be H=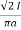
= 
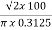=144 AT/m
Value of H at the centre of circle is H=I/2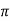
r
=125.6AT/m
Bar Magnet:
All magnets have two regions called magnetic poles with the magnetism both in and around a magnetic circuit producing a definite chain of organised and balanced pattern of invisible lines of flux around it. These lines of flux are called as the magnetic field of the magnet. At each end of a magnet is a pole. Magnetic poles are always present in pairs, there is always a region of the magnet called the North-pole and there is always an opposite region called the South-pole. The lines which go to make up a magnetic field showing the direction and intensity are called Lines of Force or Magnetic Flux and represented as Phi ( Φ ).
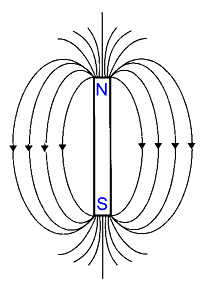
- Lines of force never cross.
- Lines of force are continuous.
- Lines of force always form individual closed loops around the magnet.
- Lines of force have a definite direction from North to South.
- Lines of force that are close together indicate a strong magnetic field.
- Lines of force that are farther apart indicate a weak magnetic field.
Like poles of the magnet repel each other and unlike poles attract each other.
Magnetic flux density =Magnet flux/Area
B=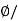
A Tesla
Current carrying coil:
The magnetic field lines are concentric circles at every point of a current carrying circular loop. The direction of magnetic field of every section of the circular loop can be found by using the right-hand thumb rule.
- At the centre of the circular loop, magnetic field lines are straight.
- Each segment of circular loop carrying current produces magnetic field lines in the same direction with in the loop.
- The direction of magnetic field at the centre of circular coil is perpendicular to the place of the coil. i.e. along the axis of the coil.
Factors affecting the strength of magnetic field
- The magnitude of magnetic field is directly proportional to the magnitude of current through the loop. i.e. B∝I.
- The magnitude of magnetic field is inversely proportional to the radius of the circular loop. i.e. B∝1/r.
Que) The amount of flux present in around magnetic bar was measured at 0.013 weber. If the material has a diameter of 14cm, calculate the flux density.
Sol: Area=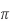
r2
Diameter=2r
r=14/2=7cm=0.07m
Area=3.14 x 0.072=0.0154m2
Flux Density B==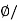
A=0.013/0.0154=0.843 Tesla
Que) Calculate the radius of the material having flux density of 0.5 T and flux present around the magnetic bar is 0.02T.
Sol: Flux Density B=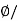
A
A=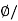 
B=0.02/0.5=0.04 m2
Area=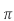
r2
r=0.113m
A highly permeable substance like ferromagnetic materials allow the magnetic lines of forces to pass through them easily. When a ferromagnetic material is placed in the magnetic field the magnetic lines of forces are concentrated inside the substance.
