Unit 4
Single-phase induction motor
Construction:
Like any other electrical motor asynchronous motor also have two main parts namely rotor and stator.
1. Stator:
As its name indicates stator is a stationary part of the induction motor. A single-phase AC supply is given to the stator of a single-phase induction motor.
2. Rotor:
The rotor is a rotating part of an induction motor. The rotor connects the mechanical load through the shaft. The rotor in the single-phase induction motor is of squirrel cage rotor type.
The construction of a single-phase induction motor is almost similar to the squirrel cage three-phase induction motor. But in the case of a single-phase induction motor, the stator has two windings instead of one three-phase winding in a three-phase induction motor.
4.1.1 Stator of Single-Phase Induction Motor
1. The stator of the single-phase induction motor has laminated stamping to reduce eddy current losses on its periphery.
2. The slots are provided on its stamping to carry stator or main winding. Stampings are made up of silicon steel to reduce the hysteresis losses.
3. When we apply a single-phase AC supply to the stator winding, the magnetic field gets produced, and the motor rotates at speed slightly less than the synchronous speed Ns. Synchronous speed Ns is given by
Where,
f = supply voltage frequency,
P = No. of poles of the motor.
4. The construction of the stator of the single-phase induction motor is similar to that of a three-phase induction motor except there are two dissimilarities in the winding part of the single-phase induction motor.
5. Firstly, the single-phase induction motors are mostly provided with concentric coils. We can easily adjust the number of turns per coil can with the help of concentric coils. The mmf distribution is almost sinusoidal.
6. Except for the shaded pole motor, the asynchronous motor has two stator windings namely the main winding and the auxiliary winding. These two windings are placed in space quadrature to each other.
4.1.2 Rotor of Single Phase Induction Motor
1. The construction of the rotor of the single-phase induction motor is similar to the squirrel cage three-phase induction motor.
2. The rotor is cylindrical and has slots all over its periphery.
3.The slots are not made parallel to each other but are a little bit skewed as the skewing prevents magnetic locking of stator and rotor teeth and makes the working of induction motor more smooth and quieter (i.e. less noisy).
4. The squirrel cage rotor consists of aluminium, brass, or copper bars. These aluminium or copper bars are called rotor conductors and placed in the slots on the periphery of the rotor. The copper or aluminium rings permanently short the rotor conductors called the end rings.
5. To provide mechanical strength, these rotor conductors are braced to the end ring and hence form a complete closed circuit resembling a cage and hence got its name as squirrel cage induction motor.
6. As end rings permanently short the bars, the rotor electrical resistance is very small and it is not possible to add external resistance as the bars get permanently shorted. The absence of slip ring and brushes make the construction of single-phase induction motor very simple and robust.
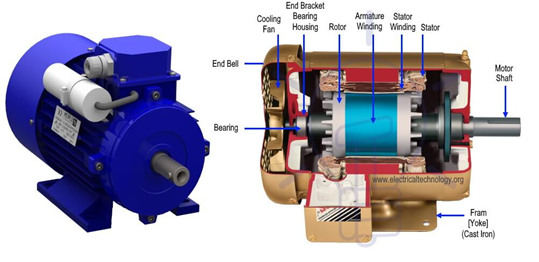
Fig 1. Constructional features
Key takeaways:
1. The slots are provided on its stamping to carry stator or main winding. Stampings are made up of silicon steel to reduce the hysteresis losses.
2. To provide mechanical strength, these rotor conductors are braced to the end ring and hence form a complete closed circuit resembling a cage and hence got its name as squirrel cage induction motor.
1. The double-revolving field theory of a single-phase induction motor states that a pulsating magnetic field is resolved into two rotating magnetic fields.
2. They are equal in magnitude but opposite in directions. The induction motor responds to each of the magnetic fields separately.
3. The net torque in the motor is equal to the sum of the torque due to each of the two magnetic fields.
The equation for an alternating magnetic field is given as:
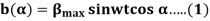
4. Where βmax is the maximum value of the sinusoidally distributed air-gap flux density produced by a properly distributed stator winding carrying an alternating current of the frequency ω, and α is the space displacement angle measured from the axis of the stator winding.
As we know,
)
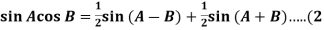So, the equation (1) can be written as
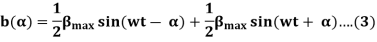
5. The first term of the right-hand side of the equation (2) represents the revolving field moving in the positive α direction. It is known as a Forward Rotating field. Similarly, the second term shows the revolving field moving in the negative α direction and is known as the Backward Rotating field.
6. The direction in which the single-phase motor is started initially is known as the positive direction. Both the revolving field rotates at the synchronous speed. ωs = 2πf in the opposite direction. Thus, the pulsating magnetic field is resolved into two rotating magnetic fields. Both are equal in magnitude and opposite in direction but at the same frequency.
7. At the standstill condition, the induced voltages are equal and opposite as a result; the two torques are also equal and opposite. Thus, the net torque is zero and, therefore, a single-phase induction motor has no starting torque.
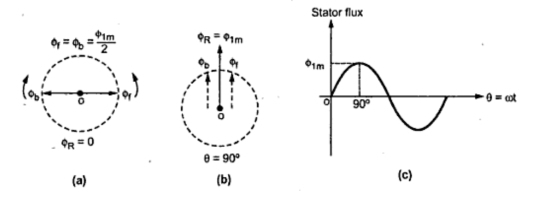
Fig 2. Double revolving field theory
Key takeaways:
1. The net torque in the motor is equal to the sum of the torque due to each of the two magnetic fields.
2. At the standstill condition, the induced voltages are equal and opposite as a result; the two torques are also equal and opposite.
1. The equivalent circuit of any machine shows the various parameter of the machine such as its Ohmic losses and also other losses.
2. The losses are modeled just by inductor and resistor.
3. The copper losses have occurred in the windings so the winding resistance is taken into account. Also, the winding has inductance for which there is a voltage drop due to inductive reactance, and also a term called power factor comes into the picture. There are two types of equivalent circuits in the case of a three-phase induction motor-
Exact Equivalent Circuit
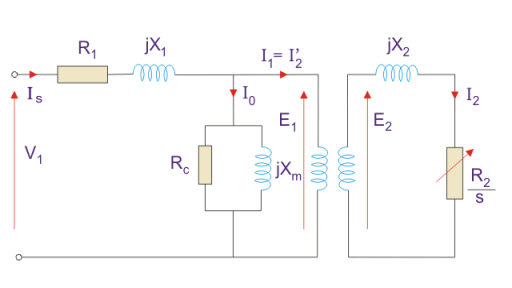
Fig 3. Equivalent Circuit
Here, R1 is the winding resistance of the stator.
X1 is the inductance of the stator winding.
Rc is the core loss component.
XM is the magnetizing reactance of the winding.
R2/s is the power of the rotor, which includes output mechanical power and copper loss of the rotor.
If we draw the circuit with referred to the stator then the circuit will look like-
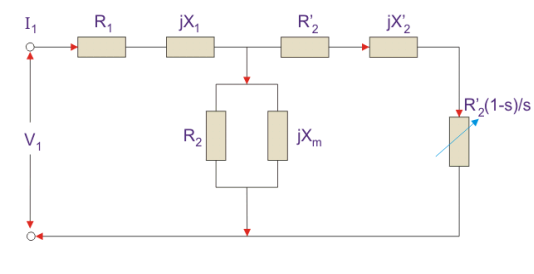
Fig 4. Equivalent circuit
Here all the other parameters are the same except-
R2’ is the rotor winding resistance referred to as stator winding.
X2’ is the rotor winding inductance referred to as stator winding.
R2 (1 – s) / s is the resistance that shows the power which is converted to mechanical power output or useful power. The power dissipated in that resistor is the useful power output or shaft power.
4. The approximate equivalent circuit is drawn just to simplify our calculation by deleting one node. The shunt branch is shifted towards the primary side.
5. This has been done as the voltage drop between the stator resistance and inductance is less and there is not much difference between the supply voltage and the induced voltage.
However, this is not appropriate due to the following reasons-
1. The magnetic circuit of the induction motor has an air gap so the exciting current is larger compared to the transformer so an exact equivalent circuit should be used.
2. The rotor and stator inductance is larger in the induction motor.
3. In an induction motor, we use distributed windings.
4. This model can be used if the approximate analysis has to be done for large motors. For smaller motors, we cannot use this.
Key takeaways:
1. The winding has inductance for which there is a voltage drop due to inductive reactance and also a term called power factor comes into the picture.
2. This has been done as the voltage drop between the stator resistance and inductance is less and there is not much difference between the supply voltage and the induced voltage.
3. The magnetic circuit of the induction motor has an air gap so the exciting current is larger compared to the transformer so an exact equivalent circuit should be used.
1. A stationary pulsating magnetic field might be resolved into two rotating fields, both having equal magnitude but opposite in direction.
2. So the net torque induced is zero at standstill. Here, the forward rotation is called the rotation with slip s, and the backward rotation is given with a slip of (2 – s). The equivalent circuit is-
Fig 5. Equivalent circuit
3. In most cases the core loss component r0 is neglected as this value is quite large and does not affect much in the calculation.
4. Here, Zf shows the forward impedance and Zb shows the backward impedance.
Also, the sum of forwarding and backward slip is 2 so in case of a backward slip, it is replaced by (2 – s).
R1 = Resistance of the stator winding.
X1 = Inductive reactance of the stator winding.
Xm = Magnetising reactance.
R2’ = Rotor Reactance with referred to the stator.
X2’ = Rotor inductive reactance with referred to the stator.
Key takeaways:
1. A stationary pulsating magnetic field might be resolved into two rotating fields, both having equal magnitude but opposite in direction
2. The net torque induced is zero at a standstill
1. The Split Phase Motor is also known as a Resistance Start Motor. It has a single cage rotor, and its stator has two windings known as main winding and starting winding.
2. Both the windings are displaced 90 degrees in space. The main winding has very low resistance and a high inductive reactance whereas the starting winding has high resistance and low inductive reactance.
3. Split-Phase-Induction-Motor-resistor is connected in series with the auxiliary winding. The current in the two windings is not equal as a result the rotating field is not uniform.
4. Hence, the starting torque is small, of the order of 1.5 to 2 times of the starting running torque. At the starting of the motor both the windings are connected in parallel.
5. As soon as the motor reaches the speed of about 70 to 80 % of the synchronous speed the starting winding is disconnected automatically from the supply mains.
6. If the motors are rated about 100 Watt or more, a centrifugal switch is used to disconnect the starting winding and for the smaller rating motors relay is used for the disconnecting of the winding.
7. A relay is connected in series with the main winding. In the starting, the heavy current flows in the circuit, and the contact of the relay gets closed.
8. Thus, the starting winding is in the circuit, and as the motor attains the predetermined speed, the current in the relay starts decreasing. Therefore, the relay opens and disconnects the auxiliary winding from the supply, making the motor runs on the main winding only.
The phasor diagram of the Split Phase Induction Motor is shown below.
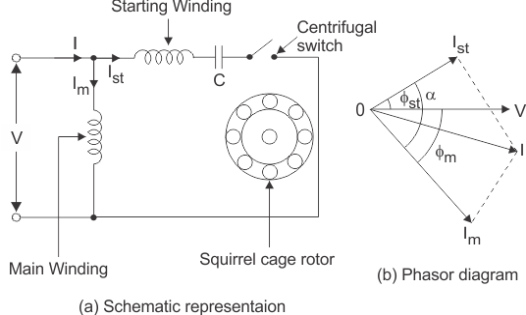
Fig 6. Schematic diagram and phasor diagram of split-phase induction motor
9. Split-Phase-Induction-Motor-The current in the main winding (IM) lag behind the supply voltage V almost by the 90-degree angle. The current in the auxiliary winding IA is approximately in phase with the line voltage.
10. Thus, there exists a time difference between the currents of the two windings. The time phase difference ϕ is not 90 degrees, but of the order of 30 degrees. This phase difference is enough to produce a rotating magnetic field.
Applications of Split Phase Induction Motor
This type of motors are cheap and are suitable for easily starting loads where the frequency of starting is limited. This type of motor is not used for drives that require more than 1 KW because of the low starting torque. The various applications are as follows:-
1. Used in the washing machine, and air conditioning fans.
2. The motors are used in mixer grinder, floor polishers.
3. Blowers, Centrifugal pumps
4. Drilling and lathe machine.
Key takeaways:
1. As soon as the motor reaches the speed of about 70 to 80 % of the synchronous speed the starting winding is disconnected automatically from the supply mains.
2. This type of motor is not used for drives that require more than 1 KW because of the low starting torque
4.7.1. Permanent split capacitor method [psc]
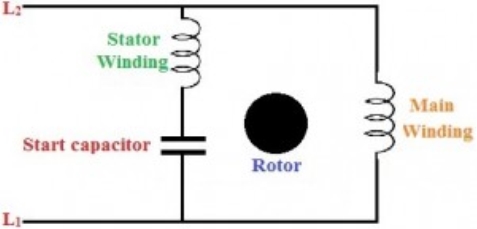
Fig 7. Permanent split capacitor method [psc]
1. In a capacitor start method, a capacitor has to be disconnected after the motor reaches a specific speed of the motor.
2. But in this method, a run-type capacitor is placed in series with the start winding or auxiliary winding. This capacitor is used continuously, and it doesn’t require any switch to disconnect it as it is not used to start the motor only.
3.The starting torque of the PSC is similar to the spilt-phase motors, but with a low starting current.
4.7.2 Capacitor start and capacitor run
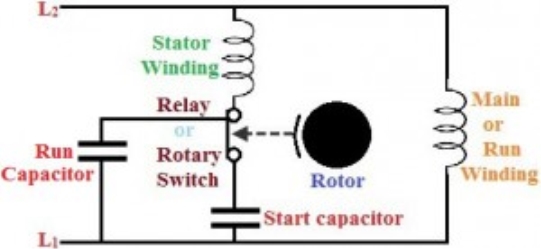
Fig 8. Capacitor Start Capacitor Run
1. The features of the capacitor start and PSC methods can be combined with this method.
2. Run capacitor is connected in series with the start winding or auxiliary winding, and a start capacitor is connected in the circuit using a normally closed switch while starting the motor.
3. Start capacitor provides starting boost to the motor and PSC provides a high running to the motor. It is more costly but still facilitates high starting and breakdown torque along with smooth running characteristics at high horsepower ratings.
Key takeaways:
1. This capacitor is used continuously, and it doesn’t require any switch to disconnect it as it is not used to start the motor only.
2. Start capacitor provides starting boost to the motor and PSC provides a high running to the motor.
Input power to stator- 3 V1I1Cos(Ɵ).
Where V1 is the stator voltage applied.
I1 is the current drawn by the stator winding.
Cos(Ɵ) is the stator power stator.
Rotor input =
Power input- Stator copper and iron losses.
Rotor Copper loss = Slip × power input to the rotor.
Developed Power = (1 – s) × Rotor input power.
Equivalent Circuit of a Single-Phase Induction Motor
1. There is a difference between single-phase and three-phase equivalent circuits. The single-phase induction motor circuit is given by double-revolving field theory which states that-a stationary pulsating magnetic field might be resolved into two rotating fields, both having equal magnitude but opposite in direction.
2. So the net torque induced is zero at standstill. Here, the forward rotation is called the rotation with slip s, and the backward rotation is given with a slip of (2 – s). The equivalent circuit is-
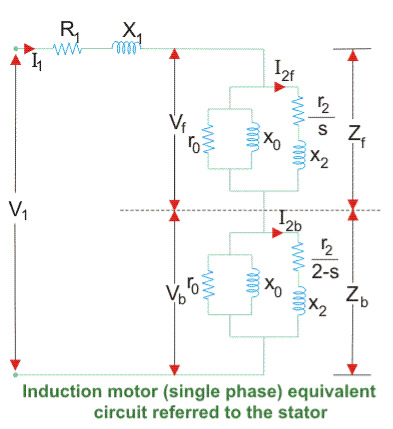
Fig 9. Development of equivalent circuit
3. Equivalent circuit of a single-phase induction motor
In most cases, the core loss component r0 is neglected as this value is quite large and does not affect much in the calculation.
Here, Zf shows the forward impedance and Zb shows the backward impedance.
Also, the sum of forwarding and backward slip is 2 so in the case of a backward slip, it is replaced by (2 – s).
R1 = Resistance of the stator winding.
X1 = Inductive reactance of the stator winding.
Xm = Magnetising reactance.
R2’ = Rotor Reactance with referred to the stator.
X2’ = Rotor inductive reactance with referred to the stator.
4. Calculation of Power of Equivalent Circuit
Find Zf and Zb.
Find stator current which is given by Stator voltage/Total circuit impedance.
Then find the input power which is given by
Stator voltage × Stator current × Cos(Ɵ)
Where Ɵ is the angle between the stator current and voltage.
Power Developed (Pg) is the difference between forwarding field power and backward power. The forward and backward power is given by the power dissipated in the respective resistors.
The rotor copper loss is given by- slip × Pg.
Output Power is given by-
Pg – s × Pg – Rotational loss.
The rotational losses include friction loss, windage loss, Core loss.
Efficiency can also be calculated by diving output power by the input power.
Key takeaways:
1. Power Developed (Pg) is the difference between forwarding field power and backward power. The forward and backward power is given by the power dissipated in the respective resistors.
2. The forward rotation is called the rotation with slip s and the backward rotation is given with a slip of (2 – s)
1.8.1 Blocked rotor test
1. The induction motors are widely used in industries and consume maximum power. To improve its performance characteristics certain tests have been designed like no-load test and block rotor test, etc.
2. A blocked rotor test is normally performed on an induction motor to find out the leakage impedance.
3. Apart from it, other parameters such as torque, motor, short-circuit current at normal voltage, and many more could be found from this test. The blocked rotor test is analogous to the short circuit test of the transformer.
4. Here shaft of the motor is clamped i.e. blocked so it cannot move and rotor winding is short-circuited.
5.In slip ring motor rotor winding is short-circuited through slip rings and in cage motors, rotor bars are permanently short-circuited.
6. The testing of the induction motor is a little bit complex as the resultant value of leakage impedance may get affected by rotor position, rotor frequency, and magnetic dispersion of the leakage flux path.
7.These effects could be minimized by conducting a blocking rotor current test on squirrel-cage rotors.
Process of Testing of Blocked Rotor Test of Induction Motor
1. In the blocked rotor test, it should be kept in mind that the applied voltage on the stator terminals should be low otherwise normal voltage could damage the winding of the stator.
2. In the block rotor test, the low voltage is applied so that the rotor does not rotate and its speed becomes zero and full load current passes through the stator winding.
3. The slip is unity related to zero speed of rotor hence the load resistance becomes zero. Now, slowly increase the voltage in the stator winding so that the current reaches its rated value.
4. At this point, note down the readings of the voltmeter, wattmeter, and ammeter to know the values of voltage, power, and current. The test can be repeated at different stator voltages for the accurate value.
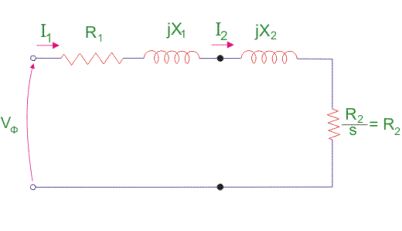
Fig 10. Block rotor test
5. Calculations of Blocked Rotor Test of Induction Motor
Resistance and Leakage Reactance Values
In blocked rotor test, core loss is very low due to the supply of low voltage and frictional loss is also negligible as the rotor is stationary, but stator copper losses and the rotor copper losses are reasonably high.
Let us take denote copper loss by Wcu.
Calculations of Blocked Rotor Test of Induction Motor
Resistance and Leakage Reactance Values
In blocked rotor test, core loss is very low due to the supply of low voltage and frictional loss is also negligible as the rotor is stationary, but stator copper losses and the rotor copper losses are reasonably high.
Let us take denote copper loss by Wcu.
Therefore,
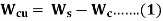
Where Wc = core loss
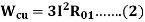
Where R01 = Motor winding of stator and rotor as per phase referred to the stator.
Thus,
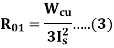
Now let us consider
Is = short circuit current
Vs = short circuit voltage
Z0 = short circuit impedance as referred to stator
Therefore,
X01 = Motor leakage reactance per phase referred to stator can be calculated as
Stator reactance X1 and rotor reactance per phase referred to as stator X2 is normally assumed equal.
Therefore,
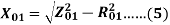
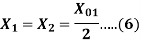
Similarly, stator resistance per phase R1 and rotor resistance per phase referred to stator R2 can be calculated as follows:
First, some suitable test is done on stator windings to find the value of R1 and then to find R2 subtract the R1 from R01
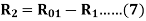
Short Circuit Current for Normal Supply Voltage
To calculate short circuit current Isc at normal voltage V of the stator, we must note short-circuit current Is and low voltage Vs applied to the stator winding.
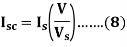
Key takeaways:
1. In the blocked rotor test, it should be kept in mind that the applied voltage on the stator terminals should be low otherwise normal voltage could damage the winding of the stator.
2. The testing of the induction motor is a little bit complex as the resultant value of leakage impedance may get affected by rotor position, rotor frequency, and magnetic dispersion of the leakage flux path.
3. To calculate short circuit current Isc at normal voltage V of the stator, we must note short-circuit current Is and low voltage Vs applied to the stator winding.
4.8.2 No-load test
1. The impedance of magnetizing path of the induction motor is large enough to obstruct the flow of current. Therefore, a small current is applied to the machine due to which there is a fall in the stator-impedance value, and rated voltage is applied across the magnetizing branch.
2. But the drop in stator-impedance value and power dissipated due to stator resistance is very small in comparison to the applied voltage. Therefore, their values are neglected and it is assumed that total power drawn is converted into core loss.
3. The air gap in a magnetizing branch in an induction motor slowly increases the exciting current and the no-load stator I2R loss can be recognized.
4. One should keep in mind that the current should not exceed its rated value otherwise rotor accelerates beyond its limit.
5. The test is performed at poly-phase voltages and rated frequency applied to the stator terminals. When the motor runs for some time and bearings get lubricated fully, at that time readings of applied voltage, input current, and input power are taken.
6. To calculate the rotational loss, subtract the stator I2R losses from the input power.
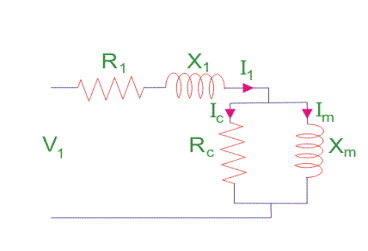
Fig 11. No-load test
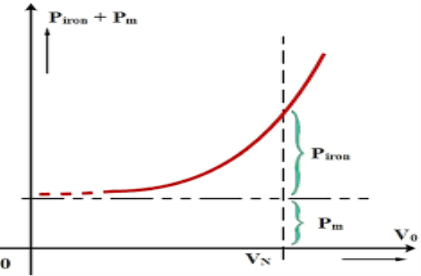
Fig 12. Graph for no-load test
Calculation of No-Load Test of Induction Motor
Let the total input power supplied to the induction motor be W0 watts.
Where,
V1 = line voltage
I0 = No-load input current
Rotational loss = W0 – S1
Where,
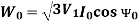…….(1)
S1 = stator winding loss = Nph I2 R1
Nph = Number phase
The various losses like windage loss, core loss, and rotational loss are fixed losses that can be calculated by
Stator winding loss = 3Io2R1
Where,
I0 = No load input current
R1 = Resistance of the motor
Core loss = 3GoV2
Key takeaways:
1. The impedance of magnetizing path of induction motor is large enough to obstruct the flow of current
2. One should keep in mind that the current should not exceed its rated value otherwise rotor accelerates beyond its limit.
References :
1. A. E. Fitzgerald and C. Kingsley, "Electric Machinery”, McGraw Hill Education,2013.
2. M. G. Say, “Performance and design of AC machines”, CBS Publishers,2002.
3. P. S. Bimbhra, “Electrical Machinery”, Khanna Publishers,2011.
4. I. J. Nagrath and D. P. Kothari, “Electric Machines”, McGraw Hill Education,2010.
5. A. S. Langsdorf, “Alternating current machines”, McGraw Hill Education,1984.
6. P. C. Sen, “Principles of Electric Machines and Power Electronics”, John Wiley & Sons,2007.
