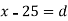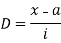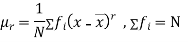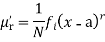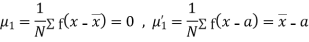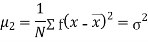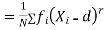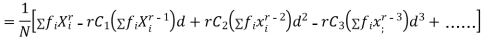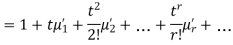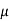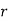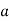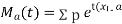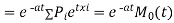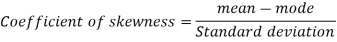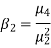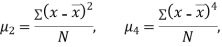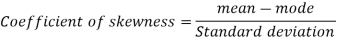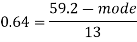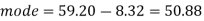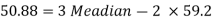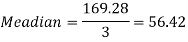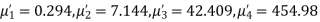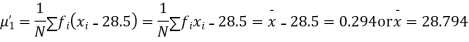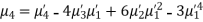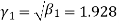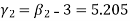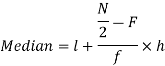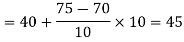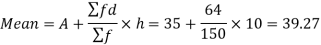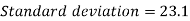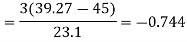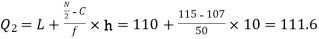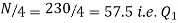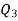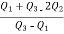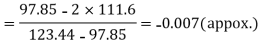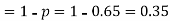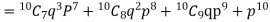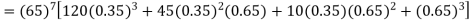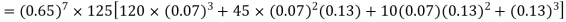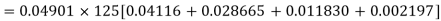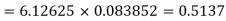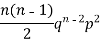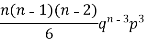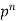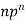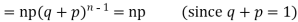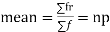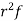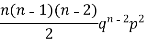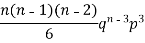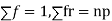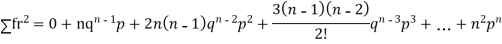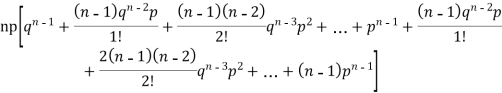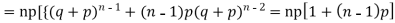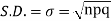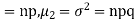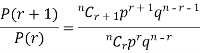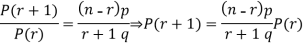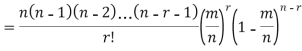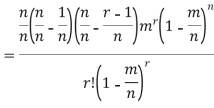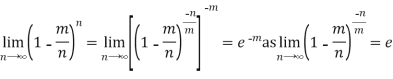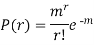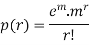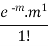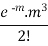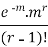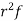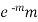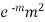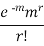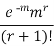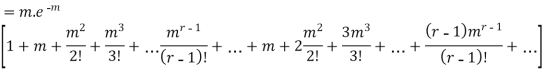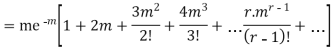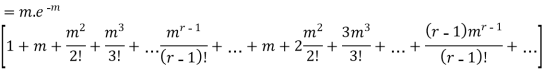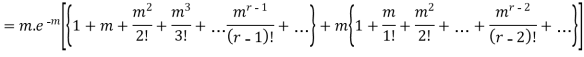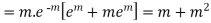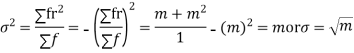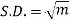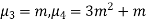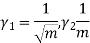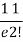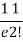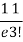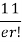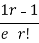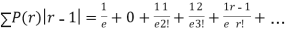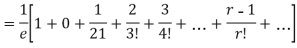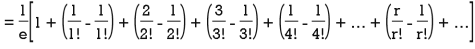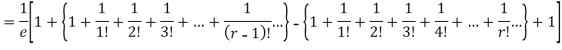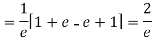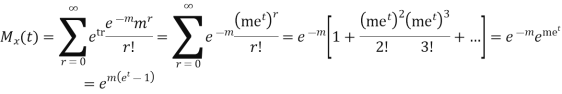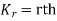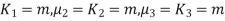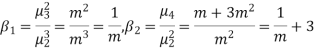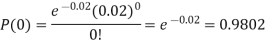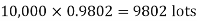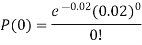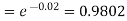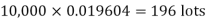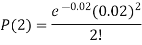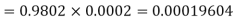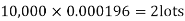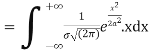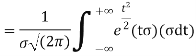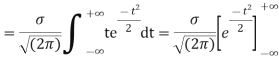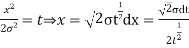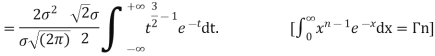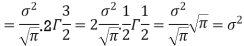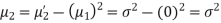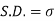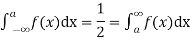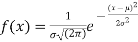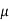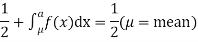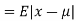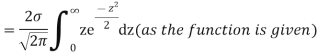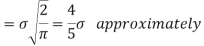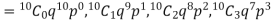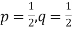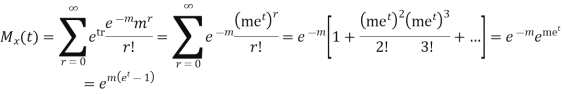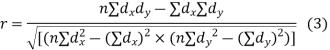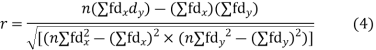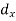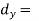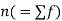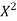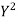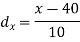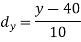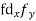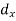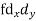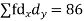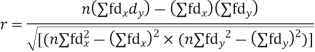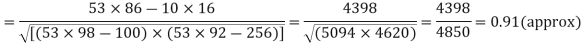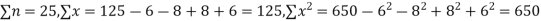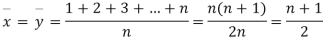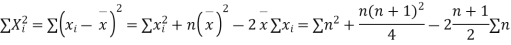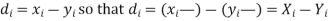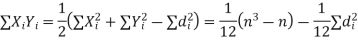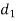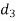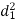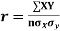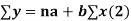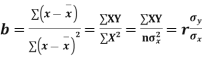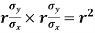Unit IV
Basic Statistics
Average or measures of Central tendency
An average is a value which is representative of a set of data. Average value may also be termed as measures of Central tendency. There are five types of averages in common.
(i) Arithmetic average or mean
(ii) Median
(iii) Mode
(iv) Geometric mean
(v) Harmonic mean
Arithmetic mean
If 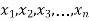 are n numbers then their arithmetic mean (A.M) is defined by
are n numbers then their arithmetic mean (A.M) is defined by
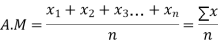
If the number  occurs
occurs  times
times 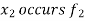 X and so on then
X and so on then

This is known as direct method.
Example 1. Find the mean of 20, 22, 25, 28, 30.
Solution. 
Example 2. Find the mean of the following:
Numbers | 8 | 10 | 15 | 20 |
Frequency | 5 | 8 | 8 | 4 |
Solution. 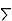 fx = 8×5 + 10×8 + 15×8 + 20×4 = 40+80+120+80=320
fx = 8×5 + 10×8 + 15×8 + 20×4 = 40+80+120+80=320
 f = 5+8+8+4=25
f = 5+8+8+4=25
A.M.= 
(b) Short cut method
Let a be the assumed mean, d the derivation of the variate x from a. Then
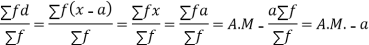
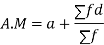
Example 3. Find the arithmetic mean for the following distribution
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
Solution. Let assumed mean (a) = 25
Class | Mid-value (x) | Frequency (f) |
| fd |
0-10 | 5 | 7 | -20 | -140 |
10-20 | 15 | 8 | -10 | -80 |
20-30 | 25 | 20 | 0 | 0 |
30-40 | 35 | 10 | + 10 | +100 |
40-50 | 45 | 5 | + 20 | +100 |
Total |
| 50 |
| -20 |
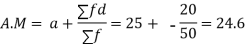
(C) Step diffusion method
Let a be the assumed mean, i the width of the class interval and
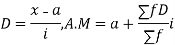
Example 4. Find the arithmetic mean of the data given in example 3 by step deviation method.
Solution. Let a =25
Class | Mid-value x | Frequency F |
| f.D |
0-10 | 5 | 7 | -2 | -14 |
10-20 | 15 | 8 | -1 | -8 |
20-30 | 25 | 20 | 0 | 0 |
30-40 | 35 | 10 | +1 | +10 |
40-50 | 45 | 5 | +2 | +10 |
Total |
| 50 |
| -2 |
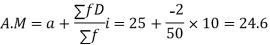
Median
Median is defined as the measure of the central atom when they are arranged in ascending or descending order of magnitude.
When the total number of the items is odd and equal to say n of 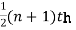 item gives the median.
item gives the median.
When the total number of The frequencies is even, say n, then there are two middle items and so the mean of the values of 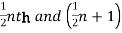 th items is the median.
th items is the median.
Example 5. Find the median of 6, 8, 9, 10, 11, 12, 13.
Solution. Total number of items =7
The middle item 
Median= value of the 4th item = 10
For grouped data, median 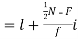
Where l is the lower limit of the median class, f is the frequency of the class, i is the width of the class interval, F is the total of all the the preceding frequencies of the median class and N is total frequency of the data.
Example 6. Find the value of median from the following data
Number of days for which absent (less than) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
Number of students | 29 | 224 | 465 | 582 | 634 | 644 | 650 | 653 | 655 |
Solution. The given cumulative frequency distribution will first be converted into ordinary frequency as under:
Class interval | Cumulative frequency | Ordinary frequency |
0-5 | 29 | 29=29 |
5-10 | 224 | 224-29=105 |
10-15 | 465 | 465-224=241 |
15-20 | 582 | 582-465=117 |
20-25 | 634 | 634-582=52 |
25-30 | 644 | 644-634=10 |
30-35 | 650 | 650-644=6 |
35-40 | 653 | 653-650=3 |
40-45 | 655 | 655-653=2 |
Median = size of 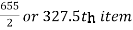
327.5th item lies in 10-15 which is the median class

Where l stands for lower limit of median class.
N stands for the total frequency
C stands for cumulative frequency just preceding the median class
i stands for class interval
f stands for frequency for the median class

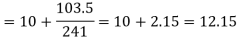
Mode
Mode is defined to be the size of the variable which occurs most frequently.
Example 7. Find the mode of the following items
0,1,6,7,2,3,7,6,6,2,6,0,5,6,0.
Solution. 6 occurs 5 times and no other item occurs 5 or more than 5 times, hence the mode is 6.
For grouped data, 
Where l is the lower limit of the modal class, f is the frequency of the modal class, i is the width of the class,  is the frequency before the model class and
is the frequency before the model class and 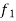 frequency of the modal class.
frequency of the modal class.
Empirical formula
Mean – Mode =3 [Mean – Median]
Example 8. Find the mode from the following data
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
Solution.
Age | Frequency | Cumulative frequency |
0-6 | 6 | 6 |
6-12 | 11 | 17 |
12-18 |
| 42 |
18-24 | 35 = f | 77 |
24-30 |
| 95 |
30-36 | 12 | 107 |
36-42 | 6 | 113 |


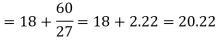
Geometric mean
If  be n values of variates x, then the geometric mean
be n values of variates x, then the geometric mean
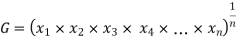
Example 10. Calculate the harmonic mean of 4,8,16.
Solution. 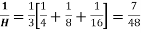
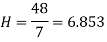
Average deviation on mean deviation
It is the mean of the absolute values of the definitions of given set of numbers from their arithmetic mean.
If 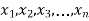 be a set of numbers with frequencies
be a set of numbers with frequencies  respectively. Let x be the arithmetic mean of the numbers
respectively. Let x be the arithmetic mean of the numbers 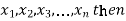
Mean deviation = 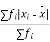
Example 11. Find the mean deviation of the following frequency distribution
Class | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
Frequency | 8 | 10 | 12 | 9 | 5 |
Solution. Let a = 15
Class | Mid-value x | Frequency f | d = x-a | fd | |x-14| | f|x-14| |
0-6 | 3 | 8 | -12 | -96 | 11 | 88 |
6-12 | 9 | 10 | -6 | -60 | 5 | 50 |
12-18 | 15 | 12 | 0 | 0 | 1 | 12 |
18-24 | 21 | 9 | +6 | 54 | 7 | 63 |
24-30 | 27 | 5 | +12 | 60 | 13 | 65 |
Total |
| 44 |
| -42 |
| 278 |

Average deviation= 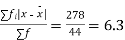
MOMENTS
The rth moment of a variable x about the mean x is usually denoted by is given by
The rth moment of a variable x aboutany point a is defined by
Relation between moments about mean and moment about any point:
In particular
|
Note. 1. The sum of the coefficients of the various terms on the right‐hand side is zero.
2. The dimension of each term on right‐hand side is the same as that of terms on the left.
MOMENT GENERATING FUNCTION
The moment generating function of the variate 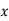 about
about  is defined as the expected value of
is defined as the expected value of 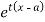 and is denoted
and is denoted  .
.
where Hence
again
|
Thus the moment generating function about the point 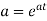 moment generating function about the origin.
moment generating function about the origin.
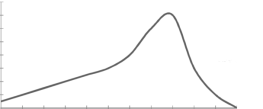
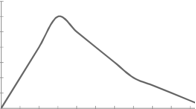
SKEWNESS:
The word skewness means lack of symmetry-
The examples of symmetric curve, positively skewed and negatively skewed curves are given as follows-
1. Symmetric curve-
|
2. Positively skewed-
|
3. Negatively skewed-
|
To measure the skewness, we use Karl Pearson’s coefficient of skewness.
Then formula is as follows-
|
Note- the value of Karl Pearson’s coefficient of skewness lies between -1 to +1.
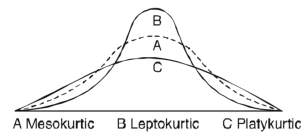
KURTOSIS:
It is the measurement of the degree of peachiness of a distribution
Kurtosis is measured as-
|
Calculation of kurtosis-
The second and fourth central moments are used to measure kurtosis.
We use Karl Pearson’s formula to calculate kurtosis-
|
Now, three conditions arises-
1. If 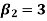 , then the curve is mesokurtic.
, then the curve is mesokurtic.
2. If  , then the curve is platykurtic
, then the curve is platykurtic
3. if 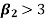 , then the curve is said to be leptokurtic.
, then the curve is said to be leptokurtic.
Example: If coefficient of skewness is 0.64. Standard deviation is 13 and mean is 59.2, then find the mode and median.
Sol.
We know that-
So that-
And we also know that-
|
Example. The first four moments about the working mean 28.5 of distribution are 0.2 94, 7.1 44, 42.409 and 454.98. Calculate the moments about the mean. Also evaluate 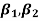 and comment upon the skewness and kurtosis of the distribution.
and comment upon the skewness and kurtosis of the distribution.
Solution.
The first four moments about the arbitrary origin 28.5 are
|
Example: Calculate the Karl Pearson’s coefficient of skewness of marks obtained by 150 students.
|
Sol. Mode is not well defined so that first we calculate mean and median-
Class | f | x | CF |
| fd |
|
0-10 | 10 | 5 | 10 | -3 | -30 | 90 |
10-20 | 40 | 15 | 50 | -2 | -80 | 160 |
20-30 | 20 | 25 | 70 | -1 | -20 | 20 |
30-40 | 0 | 35 | 70 | 0 | 0 | 0 |
40-50 | 10 | 45 | 80 | 1 | 10 | 10 |
50-60 | 40 | 55 | 120 | 2 | 80 | 160 |
60-70 | 16 | 65 | 136 | 3 | 48 | 144 |
70-80 | 14 | 75 | 150 | 4 | 56 | 244 |
Now,
And
Standard deviation-
Then-
|
Example. Calculate the median, quartiles and the quartile coefficient of skewness from the following data:
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
No. of persons | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Solution. Here total frequency 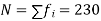
The cumulative frequency table is
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
Frequency | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Cumulative Frequency | 12 | 30 | 65 | 107 | 157 | 202 | 222 | 230 |
Now, N/2 =230/2= 115th item which lies in 110 – 120 group.
Median or Also,
Similarly 3N/4 = 172.5 i.e.
Hence quartile coefficient of skewness =
|
Key takeaways-
- Mean-
If there are n numbers in a dataset- 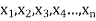 then arithmetic mean will be-
then arithmetic mean will be-

If the numbers along with frequencies are given then mean can be defined as-

2. Short cut method to find mean-
Suppose ‘a’ is assumed mean, and ‘d’ is the deviation of the variate x form a, then-
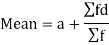
3. Step deviation method for mean-

Where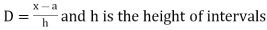
4. Median for grouped data-
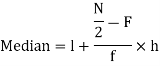
Here,
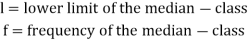
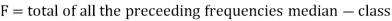


5. Mode for grouped data-
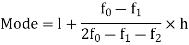
Here,
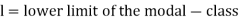




6. Mean – Mode = [Mean - Median]
7. 1. 
8. The rth moment of a variable x about the mean x is usually denoted by is given by
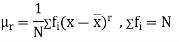
9. 
10. Karl Pearson’s formula to calculate kurtosis-

Now, three conditions arises-
1. If 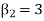 , then the curve is mesokurtic.
, then the curve is mesokurtic.
2. If 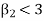 , then the curve is platykurtic
, then the curve is platykurtic
3. if  , then the curve is said to be leptokurtic.
, then the curve is said to be leptokurtic.
A probability distribution is an arithmetical function which defines completely possible values &possibilities that a random variable can take in a given range. This range will be bounded between the minimum and maximum possible values. But exactly where the possible value is possible to be plotted on the probability distribution depends on a number of influences. These factors include the distribution's mean, SD, Skewness, and kurtosis.
Binomial Distribution:
BINOMIAL DISTRIBUTION 
To find the probability of the happening of an event once, twice, thrice,…r times ….exactly in n trails.
Let the probability of the happening of an event A in one trial be p and its probability of not happening be 1 – p – q.
We assume that there are n trials and the happening of the event A is r times and its not happening is n – r times.
This may be shown as follows
AA……A 
r times n – r times (1)
A indicates its happening  its failure and P (A) =p and P (
its failure and P (A) =p and P (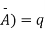
We see that (1) has the probability
pp…p qq….q=
r times n-r times (2)
Clearly (1) is merely one order of arranging r A’S.
The probability of (1) = Number of different arrangements of r A’s and (n-r)
Number of different arrangements of r A’s and (n-r) ’s
’s
The number of different arrangements of r A’s and (n-r) ’s
’s 
Probability of the happening of an event r times =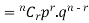
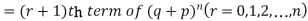
If r = 0, probability of happening of an event 0 times 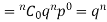
If r = 1,probability of happening of an event 1 times 
If r = 2,probability of happening of an event 2 times 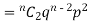
If r = 3,probability of happening of an event 3 times 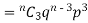 and so on.
and so on.
These terms are clearly the successive terms in the expansion of 
Hence it is called Binomial Distribution.
Example. If on an average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.
Solution. Out of 10 ships one ship is wrecked.
I.e. nine ships out of 10 ships are safe, P (safety) = 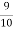
P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)

Example. The overall percentage of failures in a certain examination is 20. if 6 candidates appear in the examination what is the probability that at least five pass the examination?
Solution. Probability of failures = 20% 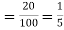
Probability of (P) = 
Probability of at least 5 pass = P(5 or 6)
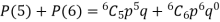

Example. The probability that a man aged 60 will live to be 70 is 0.65. what is the probability that out of 10 men, now 60, at least seven will live to be 70?
Solution. The probability that a man aged 60 will live to be 70
Number of men= n = 10 Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10) = P (7)+ P(8)+ P(9) + P(10) =
|
Example. Assuming that 20% of the population of a city are literate so that the chance of an individual being literate is  and assuming that hundred investigators each take 10 individuals to see whether they are illiterate, how many investigators would you expect to report 3 or less were literate.
and assuming that hundred investigators each take 10 individuals to see whether they are illiterate, how many investigators would you expect to report 3 or less were literate.
Solution. 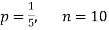
Required number of investigators = 0.879126118× 100 =87.9126118 = 88 approximate
|
Mean or binomial distribution
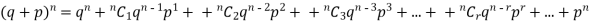
Successors r | Frequency f | rf |
0 |
| 0 |
1 |
|
|
2 |
| n(n-1) |
3 |
|
|
….. | …… | …. |
n |
|
|
Since,
|
STANDARD DEVIATION OF BINOMIAL DISTRIBUTION
Successors r | Frequency f |
|
0 |
| 0 |
1 |
|
|
2 |
| 2n(n-1) |
3 |
|
|
….. | …… | …. |
n |
|
|
We know that r is the deviation of items (successes) from 0.
Putting these values in (1) we have
Hence for the binomial distribution, Mean
|
Example. A die is tossed thrice. A success is getting 1 or 6 on a TOSS. Find the mean and variance of the number of successes.
Solution. 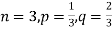
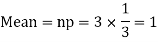
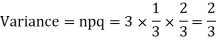
RECURRENCE RELATION FOR THE BINOMIAL DISTRIBUTION
By Binomial Distribution
On dividing (2) by (1) , we get
|
Poisson Distribution:
Poisson distribution is a particular limiting form of the Binomial distribution when p (or q) is very small and n is large enough.
Poisson distribution is

where m is the mean of the distribution.
Proof. In Binomial Distribution
Taking limits when n tends to infinity
|
MEAN OF POISSON DISTRIBUTION

Success r | Frequency f | f.r |
0 |
| 0 |
1 |
|
|
2 |
|
|
3 |
|
|
… | … | … |
r |
|
|
… | … | … |
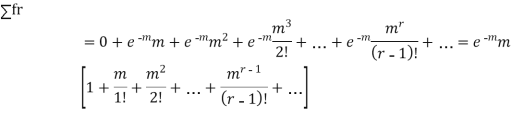
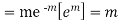

STANDARD DEVIATION OF POISSON DISTRIBUTION
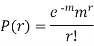
Successive r | Frequency f | Product rf | Product |
0 |
| 0 | 0 |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
……. | …….. | …….. | …….. |
r |
|
|
|
…….. | ……. | …….. | ……. |
Hence mean and variance of a Poisson distribution are equal to m. Similarly we can obtain,
|
MEAN DEVIATION
Show that in a Poisson distribution with unit mean, and the mean deviation about the mean is 2/e times the standard deviation.
Solution. 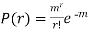 But mean = 1 i.e. m =1 and S.D. =
But mean = 1 i.e. m =1 and S.D. = 
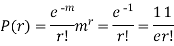
r | P (r) | |r-1| | P(r)|r-1| |
0 |
| 1 |
|
1 |
| 0 | 0 |
2 |
| 1 |
|
3 |
| 2 |
|
4 |
| 3 |
|
….. | ….. | ….. | ….. |
r |
| r-1 |
|
Mean Deviation =
|
MOMENT GENERATING FUNCTION OF POISSON DISTRIBUTION
Solution. 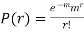
Let  be the moment generating function then
be the moment generating function then
|
CUMULANTS
The cumulant generating function 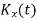 is given by
is given by
Now i.e. Mean =
|
RECURRENCE FORMULA FOR POISSON DISTRIBUTION
SOLUTION. By Poisson distribution
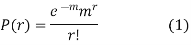

On dividing (2) by (1) we get
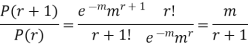
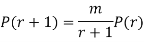
Example. Assume that the probability of an individual coal miner being killed in a mine accident during a year is 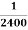 . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
Solution. 
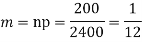

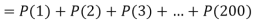
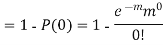
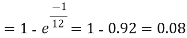
Example. Suppose 3% of bolts made by a machine are defective, the defects occuring at random during production. If bolts are packaged 50 per box, find
(a) Exact probability and
(b) Poisson approximation to it, that a given box will contain 5 defectives.
Solution. 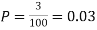
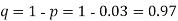
(a) Hence the probability for 5 defectives bolts in a lot of 50.

(b) To get Poisson approximation m = np =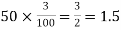
Required Poisson approximation=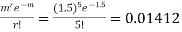
Example. In a certain factory producing cycle tyres, there is a smallchance of 1 in 500 tyres to be defective. The tyres are supplied in lots of 10. Using Poisson distribution, calculate the approximate number of lots containing no defective, one defective and two defective tyres, respectively, in a consignment of 10,000 lots.
Solution.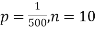
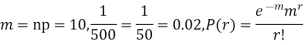
S.No. | Probability of defective | Number of lots containing defective |
1. |
|
|
2. |
|
|
3. |
|
|
Normal Distribution:
Normal Distribution
Normal distribution is a continuous distribution. It is derived as the limiting form of the Binomial distribution for large values of n and p and q are not very small.
The normal distribution is given by the equation
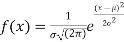 (1)
(1)
Where  = mean,
= mean,  = standard deviation,
= standard deviation, 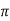 =3.14159…e=2.71828…
=3.14159…e=2.71828…

On substitution 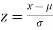 in (1) we get
in (1) we get 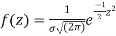 (2)
(2)
Here mean = 0, standard deviation = 1
(2) is known as standard form of normal distribution.
MEAN FOR NORMAL DISTRIBUTION
Mean
|
STANDARD DEVIATION FOR NORMAL DISTRIBUTION
Put,
|
MEDIAN OF THE NORMAL DISTRIBUTION
If a is the median then it divides the total area into two equal halves so that
Where, Suppose
|
Thus, 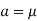
Similarly, when 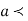 mean, we have a =
mean, we have a = 
Thus, median = mean = 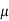
MEA DEVIATION ABOUT THE MEAN 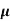
Mean deviation
|
MODE OF THE NORMAL DISTRIBUTION
We know that mode is the value of the variate x for which f (x) is maximum. Thus by differential calculus f (x) is maximum if  and
and 
Where, 
Thus mode is 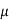 and model ordinate =
and model ordinate = 
NORMAL CURVE
Let us show binomial distribution graphically. The probabilities of heads in 1 tosses are
|
If the variates (head here) are treated as if they were continuous, the required probability curve will be a normal curve as shown in the above figure by dotted lines.
Properties of the normal curve 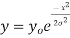
- The curve is symmetrical about the y- axis. The mean, median and mode coincide at the origin.
- The curve is drawn, if mean (origin of x) and standard deviation are given. The value of
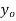 can be calculated from the fact that the area of the curve must be equal to the total number of observations.
can be calculated from the fact that the area of the curve must be equal to the total number of observations. - y decreases rapidly as x increases numerically. The curve extends to infinity on either side of the origin.
- (a)
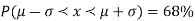
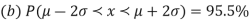
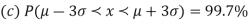
AREA UNDER THE NORMAL CURVE
By taking 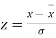 the standard normal curve is formed.
the standard normal curve is formed.
The total area under this curve is 1. The area under the curve is divided into two equal parts by z = 0. Left hand side area and right hand side area to z = 0 is 0.5. The area between the ordinate z = 0.
Example. On a final examination in mathematics, the mean was 72, and the standard deviation was 15. Determine the standard scores of students receiving graders.
(a) 60
(b) 93
(c) 72
Solution. (a) 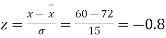
(b)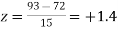
(c) 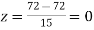
Example. Find the area under the normal curve in each of the cases
(a) Z = 0 and z = 1.2
(b) Z = -0.68 and z = 0
(c) Z = -0.46 and z = -2.21
(d) Z = 0.81 and z = 1.94
(e) To the left of z = -0.6
(f) Right of z = -1.28
Solution. (a) Area between Z = 0 and z = 1.2 =0.3849
(b)Area between z = 0 and z = -0.68 = 0.2518
(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\
= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)
=0.4865 + 0.1772 = 0.6637
(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)
= 0.4738-0.2910=0.1828
(e) Required area = 0.5-(Area between z = 0 and z = 0.6)
= 0.5-0.2257=0.2743
(f)Required area = (Area between z = 0 and z = -1.28)+0.5
= 0.3997+0.5
= 0.8997
Example. The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise the washers are considered defective. Determine the percentage of defective washers produced by the machine assuming the diameters are normally distributed.
Solution. 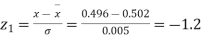

Area for non – defective washers = Area between z = -1.2
And z = +1.2
=2 Area between z = 0 and z = 1.2
=2 (0.3849)-0.7698=76.98%
(0.3849)-0.7698=76.98%
Percentage of defective washers = 100-76.98=23.02%
Example. A manufacturer knows from experience that the resistance of resistors he produces is normal with mean  and standard deviation
and standard deviation  . What percentage of resistors will have resistance between 98 ohms and 102 ohms?
. What percentage of resistors will have resistance between 98 ohms and 102 ohms?
Solution. 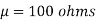 ,
,
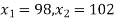


Area between 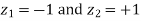
= (Area between z = 0 and z = +1)
= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826
0.3413 = 0.6826
Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26
Example. In a normal distribution, 31% of the items are 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
Solution. Let  be the mean and
be the mean and 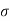 the S.D.
the S.D.
If x = 45, 
If x = 64, 
Area between 0 and 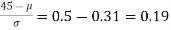
[From the table, for the area 0.19, z = 0.496)

Area between z = 0 and z =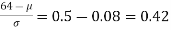
(from the table for area 0.42, z = 1.405)
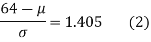
Solving (1) and (2) we get 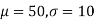
Key takeaways-
Probability of the happening of an event r times =
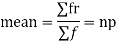
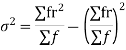
- RECURRENCE RELATION FOR THE BINOMIAL DISTRIBUTION
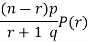
2. Poisson distribution is

where m is the mean of the distribution.
3. 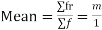
4. MOMENT GENERATING FUNCTION OF POISSON DISTRIBUTION
|
5. RECURRENCE FORMULA FOR POISSON DISTRIBUTION

6. Normal Distribution
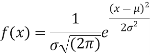
7. median = mean = 
Correlation
So far we have confined our attention to the analysis of observations on a single variable. There are however, many phenomena where the changes in one variable are related to the changes in the other variable. For instance, the yield of a crop varies with the amount of rainfall, the price of a commodity increases with the reduction in its supply and so on. Such a data connecting two variables is called bivariate population.
To obtain a measure of relationship between the two variables, we plot their corresponding values on the graph taking one of the variable along the x axis and the other along the y axis. (Figure 25.6).
Let the origin be shifted to  , where
, where  re the means of X’s and y's that the new coordinates are given by
re the means of X’s and y's that the new coordinates are given by

Now the points (X,Y) are so distributed over the four quadrants of XY plane that the product XY is positive in the first and third quadrant but negative in the second and fourth quadrants. the algebraic sum of the products can be taken as describing the trend of the dots in all the quadrants.
(i) If 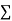 XY is positive, the trend of the dots is through the first and third quadrants.
XY is positive, the trend of the dots is through the first and third quadrants.
(ii) If 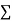 XY is negative the trend of two dots is in the second and fourth quadrants and
XY is negative the trend of two dots is in the second and fourth quadrants and
(iii) If 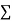 XY is zero, the points indicate no trend i.e. the points are evenly distributed over the quadrants.
XY is zero, the points indicate no trend i.e. the points are evenly distributed over the quadrants.
The 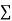 XY or better still
XY or better still 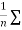 XY i.e. the average of n products may be taken as a measure of correlation. If we put X and Y in their units, i.e.
XY i.e. the average of n products may be taken as a measure of correlation. If we put X and Y in their units, i.e. 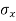 taking, as the unit for x and
taking, as the unit for x and  for y, then
for y, then
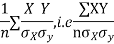
Is the measure of correlation.
Coefficient of correlation
The numerical measure of correlation is called the coefficient of correlation and is defined by the relation

Where, X = deviation from the mean =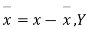 = devaluation from the mean
= devaluation from the mean 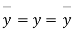
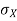 = Standard deviation of x series,
= Standard deviation of x series, 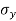 = standard deviation of y series and n = number of the values of the two variables
= standard deviation of y series and n = number of the values of the two variables
Methods of calculation
(a) Direct method. Substituting the value of
Another form of the formula (1) which is quite handy for calculation is
(b) Step deviation method. The direct method becomes very lengthy and tedious if the means of the two series are not integers. In such cases, use is made of assumed means. If
(c) Coefficient of correlation for grouped data. When x and y series are both given as frequency distributions these can be represented by a two way table known as the correlation table. the coefficient of correlation for such a bivariate frequency distribution is calculated by the formula
Where
|
Example. Psychological test of the intelligence and of Engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and Engineering ratio (E.R). Calculate the coefficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R. | 105 | 104 | 102 | 101 | 100 | 99 | 98 | 96 | 93 | 92 |
E.R. | 101 | 103 | 100 | 98 | 95 | 96 | 104 | 92 | 97 | 94 |
Solution. We construct the following table
Student | Intelligence ratio x | Engineering ratio y y |
|
| XY |
A | 105 6 | 101 3 | 36 | 9 | 18 |
B | 104 5 | 103 5 | 25 | 25 | 25 |
C | 102 3 | 100 2 | 9 | 4 | 6 |
D | 101 2 | 98 0 | 4 | 0 | 0 |
E | 100 1 | 95 -3 | 1 | 9 | -3 |
F | 99 0 | 96 - 2 | 0 | 4 | 0 |
G | 98 -1 | 104 6 | 1 | 36 | -6 |
H | 96 -3 | 92 -6 | 9 | 36 | 18 |
I | 93 -6 | 97 -1 | 36 | 1 | 6 |
J | 92 -7 | 94 -4 | 49 | 16 | 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, mean of x, i.e. 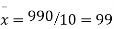 and mean of y, i.e.
and mean of y, i.e. 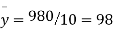
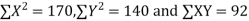
Substituting these value in the formula (1)p.744 we have

Example. The correlation table given below shows that the ages of husband and wife of 53 married couples living together on the census night of 1991. Calculate the coefficient of correlation between the age of the husband and that of the wife.
Age of husband | Age of wife | Total | ||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | |||
15-25 | 1 | 1 | - | - | - | - | 2 | |
25-35 | 2 | 12 | 1 | - | - | - | 15 | |
35-45 | - | 4 | 10 | 1 | - | - | 15 | |
45-55 | - | - | 3 | 6 | 1 | - | 10 | |
55-65 | - | - | - | 2 | 4 | 2 | 8 | |
65-75 | - | - | - | - | 1 | 2 | 3 | |
Total | 3 | 17 | 14 | 9 | 6 | 4 | 53 | |
Solution.
Age of husband | Age of wife x series | Suppose
| |||||||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
Total f | |||||||
Years | Midpoint x | 20 | 30 | 40 | 50 | 60 | 70 | ||||||
Age group | Midpoint y |
|
| -20 | -10 | 0 | 10 | 20 | 30 |
|
|
| |
| -2 | -1 | 0 | 1 | 2 | 3 | |||||||
15-25 | 20 | -20 | -2 | 4 1 | 2 1 |
|
|
|
| 2 | -4 | 8 | 6 |
25-35 | 30 | -10 | -1 | 4 2 | 12 12 | 0 1 |
|
|
| 15 | -15 | 15 | 16 |
35-45 | 40 | 0 | 0 |
| 0 4 | 0 10 | 0 1 |
|
| 15 | 0 | 0 | 0 |
45-55 | 50 |
|
|
|
| 0 3 | 6 6 | 2 1 |
| 10 | 10 | 10 | 8 |
55-65 | 60 |
|
|
|
|
| 4 2 | 16 4 | 12 2 | 8 | 16 | 32 | 32 |
65-75 | 70 |
|
|
|
|
|
| 6 1 | 18 2 | 3 | 9 | 27 | 24 |
Total f | 3 | 17 | 14 | 9 | 6 | 4 | 53 = n | 16 | 92 | 86 | |||
| -6 | -17 | 0 | 9 | 12 | 12 | 10 | Thick figures in small sqs. for Check:
From both sides | |||||
| 12 | 17 | 0 | 9 | 24 | 36 | 98 | ||||||
| 8 | 14 | 0 | 10 | 24 | 30 | 86 | ||||||
With the help of the above correlation table, we have
|
Lines of Regression
It frequently happens that the dots of the scatter diagram generally tends to cluster along a well- defined direction which suggests a linear relationship between the variables x and y. Such a line of best fit for the given distribution of dots is called the line of regression (figure 25.6). in fact there are two such lines, one giving the best possible mean values of y for each specified value pf x and the other giving the best possible mean values of x for given value of y. the former is known as the line of regression of y on x and the latter as the line of regression of x on y.
Consider first the line of regression of y on x. Let the straight line satisfying the general trend of n dots in a scatter diagram be
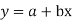 (1)
(1)
We have to determine the constant a and b so that (1) gives for each value of x, the best estimate for the average value of y in accordance with the principle of least squares therefore, the normal equation for a and b are
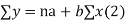

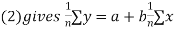 i.e.
i.e. 
This shows that 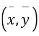 i.e. the mean of x and y lie on (1).
i.e. the mean of x and y lie on (1).
Shifting the origin to  (3) takes the form of
(3) takes the form of
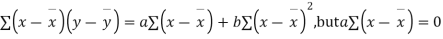

Cor. The correlation coefficient r is the geometric mean between the two regression coefficients
For 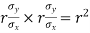
Example. The two regression equations of the variable x and y are x = 19.13 and y = 11.64 – 0.50 x. Find (i) mean of x’s (ii) mean of y’s and (iii) the correlation coefficient between x and y.
Solution. Since the mean of x’s and the mean of y’s lie on the two regression lines, we have
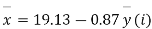
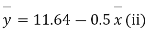
Multiplying (ii) by 0.87 and subtracting from (i) we have


Regression coefficient of y and x is -0.50 and that of x and y is -0.87.
Now since the coefficient of correlation is the geometric mean between the two regression coefficients.
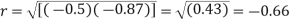
[-ve sign is taken since both the regression coefficients are –ve]
Example. If  is the angle between the two regression lines show that
is the angle between the two regression lines show that
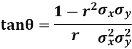
Explain the significance when 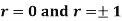 .
.
Solution. The equations to the line of regression of y on x and x on y are

Their slopes are 
Thus, 
When r = 0, i.e. when the variable are independent, the two lines of regression are perpendicular to each other.
i.e. when the variable are independent, the two lines of regression are perpendicular to each other.
When 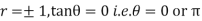 . Thus the line of regression coincide i.e. there is perfect correlationbetween the two variables.
. Thus the line of regression coincide i.e. there is perfect correlationbetween the two variables.
Example. While calculating correlation coefficient between two variables x and y from 25 pairs of observations, the following results were obtained : n = 25,  Later it was discovered at the time of checking that the pairs of values x -8,6 and y = 12, 8 were copied down as x = 6,8 and y = 14,6. Obtain the correct value of correlation coefficients.
Later it was discovered at the time of checking that the pairs of values x -8,6 and y = 12, 8 were copied down as x = 6,8 and y = 14,6. Obtain the correct value of correlation coefficients.
Solution. To get the correct results, we subtract the incorrect values and add the corresponding correct values.
The correct results would be
|
RANK CORRELATION
A group of n individuals may be arranged in order to merit with respect to some characteristics. The same group would give different orders for different characteristics. Considering the orders corresponding to two characteristics A and B, the correction between these n pairs of rank is called the rank correlation in the characteristics A and B for that group of individuals.
Let  be the ranks of the ith individuals in A and B respectively. Assuming that no two individuals are bracketed equal in either case, each of the variables taking the values 1,2,3,…,n we have
be the ranks of the ith individuals in A and B respectively. Assuming that no two individuals are bracketed equal in either case, each of the variables taking the values 1,2,3,…,n we have
If X, Y be the deviations of x, y from their means, then
Now let,
Hence the correlation coefficient between these variables is
|
This is called the rank correlation coefficient and is denoted by 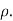
Example. Ten participants in a contest are ranked by two judges as follows:
x | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
y | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Calculate the rank correlation coefficient 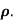
Solution. If 
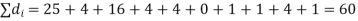
Hence, 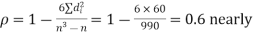
Example. Three judges A,B,C give the following ranks. Find which pair of judges has common approach
A | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
B | 3 | 5 | 8 | 4 | 7 | 10 | 2 | 1 | 6 | 9 |
C | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Solution. Here n = 10
A (=x) | Ranks by B(=y) | C (=z) |
x-y |
y - z |
z-x |
|
|
|
1 | 3 | 6 | -2 | -3 | 5 | 4 | 9 | 25 |
6 | 5 | 4 | 1 | 1 | -2 | 1 | 1 | 4 |
5 | 8 | 9 | -3 | -1 | 4 | 9 | 1 | 16 |
10 | 4 | 8 | 6 | -4 | -2 | 36 | 16 | 4 |
3 | 7 | 1 | -4 | 6 | -2 | 16 | 36 | 4 |
2 | 10 | 2 | -8 | 8 | 0 | 64 | 64 | 0 |
4 | 2 | 3 | 2 | -1 | -1 | 4 | 1 | 1 |
9 | 1 | 10 | 8 | -9 | 1 | 64 | 81 | 1 |
7 | 6 | 5 | 1 | 1 | -2 | 1 | 1 | 4 |
8 | 9 | 7 | -1 | 2 | -1 | 1 | 4 | 1 |
Total |
|
| 0 | 0 | 0 | 200 | 214 | 60 |


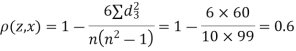
Since 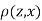 is maximum, the pair of judge A and C have the nearest common approach.
is maximum, the pair of judge A and C have the nearest common approach.
Key takeaways-
Coefficient of correlation
References:
1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
2. P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
4. W. Feller, “An Introduction to Probability Theory and its Applications”, Vol. 1, Wiley, 1968.
5. N.P. Bali and M. Goyal, “A text book of Engineering Mathematics”, Laxmi Publications, 2010.
6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
7. T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010.