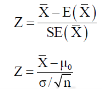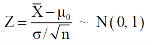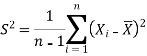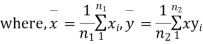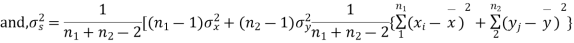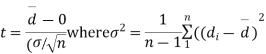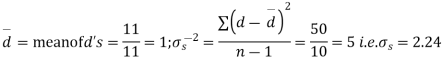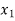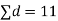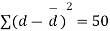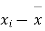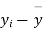Unit VI
Small samples
Test for single mean
Testing of hypothesis for population mean using Z-Tesnt
For testing the null hypothesis, the test statistic Z is given as-
|
The sampling distribution of the test statistics depends upon variance 
So that there are two cases-
Case-1: when 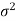 is known -
is known -
The test statistic follows the normal distribution with mean 0 and variance unity when the sample size is the large as the population under study is normal or non-normal. If the sample size is small then test statistic Z follows the normal distribution only when population under study is normal. Thus,
|
Case-1: when 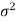 is unknown –
is unknown –
We estimate the value of 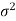 by using the value of sample variance
by using the value of sample variance
|
Then the test statistic becomes-

After that, we calculate the value of test statistic as may be the case ( is known or unknown) and compare it with the critical value at prefixed level of significance α.
is known or unknown) and compare it with the critical value at prefixed level of significance α.
Example: A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?
Sol.
It is given that-
Specified value of population mean = 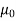 = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25
|
The null and alternative hypothesis will be-

Also the alternative hypothesis left-tailed so that the test is left tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should used t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by

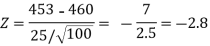
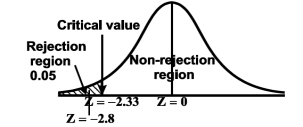
We get the critical value of left tailed Z test at 1% level of significance is 
Since calculated value of test statistic Z (= ‒2.8) is less than the critical value
(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance.
Example: A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with standard deviation 90 hours. Should the company accept the new brand at 5% level of significance?
Sol.
Here we have-
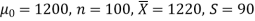
The company may accept the new CFL light when average life of
CFL light is greater than 1200 hours. So the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So our claim is 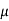 > 1200 and its complement is
> 1200 and its complement is 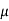 ≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,

Since the alternative hypothesis is right-tailed so the test is right-tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for Z-test instead of t-test.
Therefore, test statistic is given by
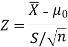

The critical values for right-tailed test at 5% level of significance is
 1.645
1.645
Since calculated value of test statistic Z (= 2.22) is greater than critical value (= 1.645), that means it lies in rejection region so we reject the null hypothesis and support the alternative hypothesis i.e. we support our claim at 5% level of significance
Thus, we conclude that sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs
Significance test of difference between sample means
Given two independent examples 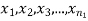 and
and  with means
with means  standard derivations
standard derivations 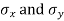 from a normal population with the same variance, we have to test the hypothesis that the population means
from a normal population with the same variance, we have to test the hypothesis that the population means  are same For this, we calculate
are same For this, we calculate
|
It can be shown that the variate t defined by (1) follows the t distribution with 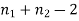 degrees of freedom.
degrees of freedom.
If the calculated value 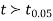 the difference between the sample means is said to be significant at 5% level of significance.
the difference between the sample means is said to be significant at 5% level of significance.
If  , the difference is said to be significant at 1% level of significance.
, the difference is said to be significant at 1% level of significance.
If 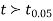 the data is said to be consistent with the hypothesis that
the data is said to be consistent with the hypothesis that 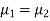 .
.
Cor. If the two samples are of same size and the data are paired, then t is defined by
|
 =difference of the ith member of the sample
=difference of the ith member of the sample
d=mean of the differences =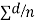 and the member of d.f.=n-1.
and the member of d.f.=n-1.
Example
Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
Sol. We compute the mean and the S.D. of the difference between the marks of the two tests as under:
|
Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.
Then,  nearly and df v=11-1=10
nearly and df v=11-1=10
Students |
|
|
|
|
|
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
|
|
|
|
we find that 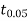 (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of  , the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
Example:
From a random sample of 10 pigs fed on diet A, the increase in weight in certain period were 10,6,16,17,13,12,8,14,15,9 lbs. For another random sample of 12 pigs fed on diet B, the increase in the same period were 7,13,22,15,12,14,18,8,21,23,10,17 lbs. Test whether diets A and B differ significantly as regards their effect on increases in weight ?
Sol. We calculate the means and standard derivations of the samples as follows
| Diet A |
|
| Diet B |
|
|
|
|
|
|
|
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 13 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 17 | 2 | 4 |
|
|
|
|
|
|
120 |
|
| 180 | 0 | 314 |

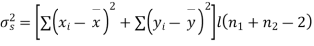

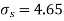
Assuming that the samples do not differ in weight so far as the two diets are concerned i.e. 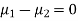
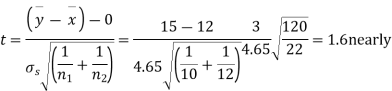

For v=20, we find  =2.09
=2.09
The calculated value of 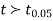
Hence the difference between the samples means is not significant i.e. thew two diets do not differ significantly as regards their effects on increase in weight.
Testing of hypothesis for difference of two population means using Z-Test-
Let there be two populations, say, population-I and population-II under study.
Also let  denote the means and variances of population-I and population-II respectively where both
denote the means and variances of population-I and population-II respectively where both 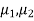 are unknown but
are unknown but  may be known or unknown. We will consider all possible cases here. For testing the hypothesis about the difference of two population means, we draw a random sample of large size n1 from population-I and a random sample of large size n2 from population-II. Let
may be known or unknown. We will consider all possible cases here. For testing the hypothesis about the difference of two population means, we draw a random sample of large size n1 from population-I and a random sample of large size n2 from population-II. Let 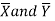 be the means of the samples selected from population-I and II respectively.
be the means of the samples selected from population-I and II respectively.
These two populations may or may not be normal but according to the central limit theorem, the sampling distribution of difference of two large sample means asymptotically normally distributed with mean 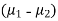 and variance
and variance 
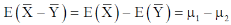
And
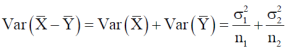
We know that the standard error = 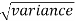
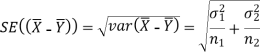
Here, we want to test the hypothesis about the difference of two population means so we can take the null hypothesis as
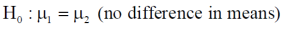
Or

And the alternative hypothesis is-
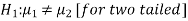
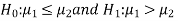
Or
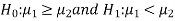
The test statistic Z is given by-
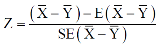
Or
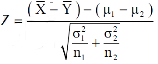
Since under null hypothesis we assume that 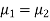 , therefore , we get-
, therefore , we get-
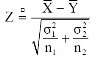
Now, the sampling distribution of the test statistic depends upon 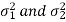 that both are known or unknown. Therefore, four cases arise-
that both are known or unknown. Therefore, four cases arise-
Case-1: When  are known and
are known and 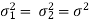
In this case, the test statistic follows normal distribution with mean
0 and variance unity when the sample sizes are large as both the populations under study are normal or non-normal. But when sample sizes are small then test statistic Z follows normal distribution only when populations under study are normal, that is,
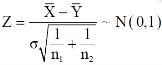
Case-2: When 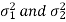 are known and
are known and 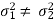
In this case, the test statistic also follows the normal distribution as described in case I, that is,

Case-3: When  are unknown and
are unknown and 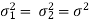
In this case, σ2 is estimated by value of pooled sample variance 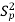
where,
|
and test statistic follows t-distribution with (n1 + n2 − 2) degrees of freedom as the sample sizes are large or small provided populations under study follow normal distribution.
But when the populations are under study are not normal and sample sizes n1 and n2are large (> 30) then by central limit theorem, test statistic approximately normally distributed with mean
0 and variance unity, that is,
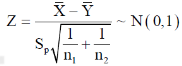
Case-4: When  are unknown and
are unknown and 
In this case, 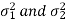 are estimated by the values of the sample variances
are estimated by the values of the sample variances  respectively and the exact distribution of test statistic is difficult to derive. But when sample sizes n1 and n2 are large (> 30) then central limit theorem, the test statistic approximately normally distributed with mean 0 and variance unity,
respectively and the exact distribution of test statistic is difficult to derive. But when sample sizes n1 and n2 are large (> 30) then central limit theorem, the test statistic approximately normally distributed with mean 0 and variance unity,
that is,

After that, we calculate the value of test statistic and compare it with the critical value at prefixed level of significance α.
Example: A college conducts both face to face and distance mode classes for a particular course indented both to be identical. A sample of 50 students of face to face mode yields examination results mean and SD respectively as-

and other sample of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:

Are both educational methods statistically equal at 5% level?
Sol. here we have-
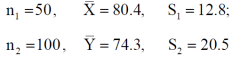
Here we wish to test that both educational methods are statistically equal. If 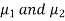 denote the average marks of face to face and distance mode students respectively then our claim is
denote the average marks of face to face and distance mode students respectively then our claim is 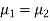 and its complement is
and its complement is 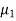 ≠
≠  . Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
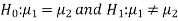
Since the alternative hypothesis is two-tailed so the test is two-tailed test.
We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So we should go for t-test if population of difference is known to be normal. But it is not the case.
Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.
For testing the null hypothesis, the test statistic Z is given by

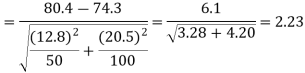
The critical (tabulated) values for two-tailed test at 5% level of significance are-

Since calculated value of Z ( = 2.23) is greater than the critical values
(= ±1.96), that means it lies in rejection region so we
reject the null hypothesis i.e. we reject the claim at 5% level of significance
Key takeaways-
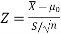
- Significance test of difference between sample means

3. Testing of hypothesis for difference of two population means using Z-Test-
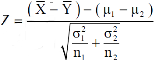
(1) CHI SQUARE  TEST
TEST
When a fair coin is tossed 80 times we expect from the theoretical considerations that heads will appear 40 times and tail 40 times. But this never happens in practice that is the results obtained in an experiment do not agree exactly with the theoretical results. The magnitude of discrepancy between observations and theory is given by the quantity 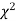 (pronounced as chi squares). If
(pronounced as chi squares). If  the observed and theoretical frequencies completely agree. As the value of
the observed and theoretical frequencies completely agree. As the value of  increases, the discrepancy between the observed and theoretical frequencies increases.
increases, the discrepancy between the observed and theoretical frequencies increases.
(1) Definition. If  and
and 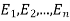 be the corresponding set of expected (theoretical) frequencies, then
be the corresponding set of expected (theoretical) frequencies, then  is defined by the relation
is defined by the relation

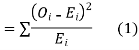

(2) Chi – square distribution
If  be n independent normal variates with mean zero and s.d. unity, then it can be shown that
be n independent normal variates with mean zero and s.d. unity, then it can be shown that 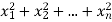 is a random variate having
is a random variate having 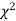 distribution with ndf.
distribution with ndf.
The equation of the  curve is
curve is
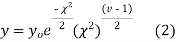
(3) Properties of  distribution
distribution
- If v = 1, the
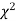 curve (2) reduces to
curve (2) reduces to 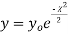 which is the exponential distribution.
which is the exponential distribution. - If
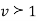 this curve is tangential to x – axis at the origin and is positively skewed as the mean is at v and mode at v-2.
this curve is tangential to x – axis at the origin and is positively skewed as the mean is at v and mode at v-2. - The probability P that the value of
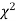 from a random sample will exceed
from a random sample will exceed  is given by
is given by
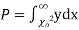
 have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)
have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)
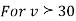 ,the
,the 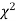 curve approximates to the normal curve and we should refer to normal distribution tables for significant values of
curve approximates to the normal curve and we should refer to normal distribution tables for significant values of 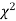 .
.
IV. Since the equation of 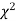 curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
V. Mean = 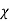 and variance =
and variance = 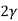
Goodness of fit
The values of  is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit given distribution
is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit given distribution 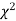 therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory and fact.
therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory and fact.
This is a nonparametric distribution free test since in this we make no assumptions about the distribution of the parent population.
Procedure to test significance and goodness of fit
(i) Set up a null hypothesis and calculate
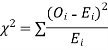
(ii) Find the df and read the corresponding values of 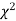 at a prescribed significance level from table V.
at a prescribed significance level from table V.
(iii) From  table, we can also find the probability P corresponding to the calculated values of
table, we can also find the probability P corresponding to the calculated values of 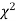 for the given d.f.
for the given d.f.
(iv) If P<0.05, the observed value of 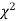 is significant at 5% level of significance
is significant at 5% level of significance
If P<0.01 the value is significant at 1% level.
If P>0.05, it is a good faith and the value is not significant.
Example. A set of five similar coins is tossed 320 times and the result is
Number of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
Solution. For v = 5, we have 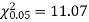
P, probability of getting a head=1/2;q, probability of getting a tail=1/2.
Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion 
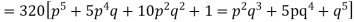
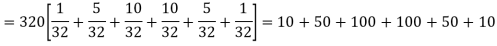
Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.
Hence, 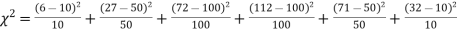


Since the calculated value of 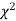 is much greater than
is much greater than 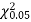 the hypothesis that the data follow the binomial law is rejected.
the hypothesis that the data follow the binomial law is rejected.
Example. Fit a Poisson distribution to the following data and test for its goodness of fit at level of significance 0.05.
x | 0 | 1 | 2 | 3 | 4 |
f | 419 | 352 | 154 | 56 | 19 |
Solution. Mean m =
Hence, the theoretical frequency are 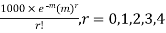
x | 0 | 1 | 2 | 3 | 4 | Total |
f | 404.9 (406.2) | 366 | 165.4 | 49.8 | 11..3 (12.6) | 997.4 |
Hence, 
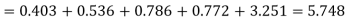
Since the mean of the theoretical distribution has been estimated from the given data and the totals have been made to agree, there are two constraints so that the number of degrees of freedom v = 5- 2=3
For v = 3, we have 
Since the calculated value of 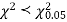 the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
Example. In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
Solution. The corresponding frequencies are

Hence, 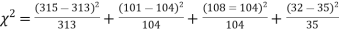

For v = 3, we have 
Since the calculated value of  is much less than
is much less than  there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
Key takeaways-
- For testing the null hypothesis, the test statistic t is given by-

2. We use test statistic F for testing the null hypothesis-
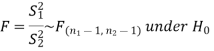

And
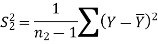
3.
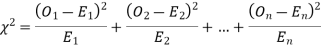

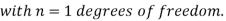
References:
1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
2. P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
4. W. Feller, “An Introduction to Probability Theory and its Applications”, Vol. 1, Wiley, 1968.
5. N.P. Bali and M. Goyal, “A text book of Engineering Mathematics”, Laxmi Publications, 2010.
6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
7. T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010.