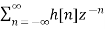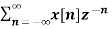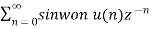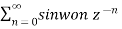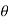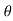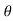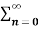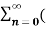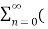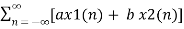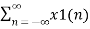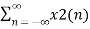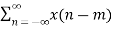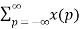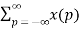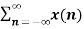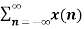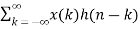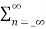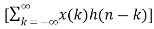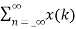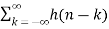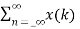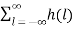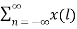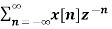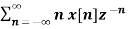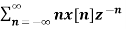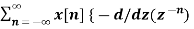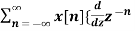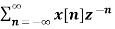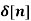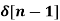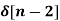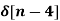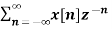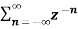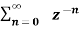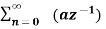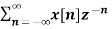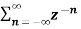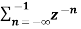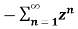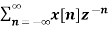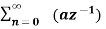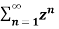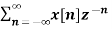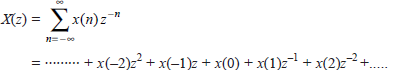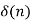The most important use of z-transform is its ability to completely characterise signals and linear systems in the most general ways possible. The z-transform is primarily used to convert the discrete time domain signal into discrete frequency domain signal. The z-transform for LTI system is defined as

H(z)=

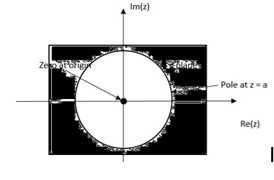
The range of variation of z for which z-transform converges is called region of convergence of z-transform.

Properties of ROC of Z-Transforms

•     ROC does not contain any poles.
•     If x(n) is a finite sequence and x(z) converges for some value of z, then ROC can be entire z plane except at z=0 and ∞.
•     If x(n) is a right sided sequence and x(z) converges for some value of z, then the ROC is the of the form |z|>Rmax where Rmax is the radius.
•     If x(n) is left sided sequence and x(z) converges for some value of z then the ROC is of the form |z|<Rmin where Rmin  is the smallest magnitude of any pole of x(z). Thus, the ROC is the entire circle having Rmin.
•     If x(n) is a double sided sequence and x(z) converges for some value of z then the ROC is of the form

R1 <|z| < R2

Rmin < |z| <Rmax.

Where R1, R2 are the magnitude of two poles of x(z)

Key takeaway

ROC does not contain any pole.

Example-1 Find the z-transform of the signal x(n) = sin w0n u(n) and find ROC.

A1) X(z) = 

X(z) = 

=       sin = ej - e-j / 2j

= 1/2j        (ejw0n – e –jwon )z-n 

= 1/2j ejwon z-1) n - e-jw0z-1) n

1/2j[ 1/1-ejw0z-1 – 1/1-e-jw0z-1]

= sin w0 z-1/ 1-2cos(wo)z-1 + z-2       ROC |z| >1

Due to its convolution property, the z-transform is a powerful tool to analyse LTI systems. From convolution property Y(z)=H(z)X(z).

Where:

Y(z)= z-transform of system output

H(z) = z-transform of impulse response

X(z)= z-transform of system input

A discrete time LTI system is causal if and only if the ROC of its system function is exterior of the circle including infinity. The ROC is the exterior of the outermost pole. H(z) is the ratio of polynomials in z, the order of numerator cannot be greater than the order of the denominator.

The LTI system is stable if and only if the ROC of the system function H(z) includes the unit circle |Z|=1. If it is a causal system it will be stable if and only if all he poles of H(z) lie inside the unit circle.

Key takeaway

1. It is possible for the system to be stable but not causal.

Linearity

If X1(z) = Z{x1(n)} and X2(z) = Z{x2(n)}

Then

Z{ax1(n) + bx2(n)} = a X1(z) + b X2(z)

Proof:

Z{ax1(n) + b x2(n) }=   z-n

= a    z-n + b   z-n 

= a X1(z) + b X2(z)

Time Shifting

If X(z) = Z{x(n)} and initial conditions for x(n) are zero then

Z{x(n-m) } = z-m X(z)

Where m is a positive integer.

Proof:

Z {x(n-m)} =   z-n

Let n-m = p then n= p+m

Z{x(n-m)} =   z –(m+p)

z-m z-p  = z-m X(z)

Multiplication by exponential sequence

If X(z ) = Z{x(n)} then

Z [ an x(n) ] = X(a-1 z)

Proof:

Z{ an x(n) } =  an z-n

        =   (az-1)n 

        = X(az-1)

Convolution

We know that

Z{x(n) * h(n) } = X(z) H(z)

Proof:

Let y(n) = x(n) * h(n)

y(n)=

Taking z-transform on both sides we obtain

Y(z) = z-n

z-k    z –(n-k)       Replacing n-k by l

  z-k    z-l

 = X(k) Z(k)

Time Reversal

If X(z) = Z{x(n)} then

   Z{x(-n)} = X(z-1}

Proof:

Z{x(-n)} = ( z-l) -1           l=-n

= X(z-1)

Multiplication by n

If Z{x(n)} = X(z) then

Z{n x(n)} = -z d/dz X(z)

          X(z) = 

        Z{n x(n)} =

                 = z -1

     = z

     =  -z }

              = -z d/dz {

 = -z d/dz X(z)

Key takeaway

Examples

1)Find the z-transform of the sequence

 x(n) = a n-1 u(n-1)

We know that x(n) = an u(n)  is

X(z) = 1/1/az-1

By using time shifting property we have Z{ x(n-k)} = z-k X(z)

Therefore

Z{an-1 u(n-1)} = z-1/ 1-az-1  = 1/z-a.            ROC |z| > |a|

2)Find the z-transform of the sequence

x(n) = an cos nπ/2

Z{ cos w0n} = 1- (cos w0) z-1/ 1 –(2 cos w0) z-1 + z-2   

Since w0=π/2

Z{ cos π/2 n u(n)} = 1/1 + z-2

Using exponential sequence property

Z{ an x(n) } = X(a-1 z)

Z{ an cos nπ/2} = 1/1+(a-1z)-2 = 1/ 1 + a2/z2  = z2/ a2 + z2  

3)Find the z transform of the sequence x(n) = n u(n)

The z-transform of unit step sequence is given by

Z{u(n)} = z/z-1

Z{ n u(n)} = -z d/dz (z/z-1)

= z/(z-1)2    

4)If x(n) = x1(n) * x2(n) where x1(n) = (1/3)n u(n) and x2(n) = (1/5)n u(n). Find X(z) by using convolution property.

X1(z) = 1/ 1- (1/3)z-1         X2(z) = 1/1- (1/5) z-1 

 X(z) = 1/1-(1/3)z-1 . 1/1-(1/5) z-1  

Using z-transform find the convolution of two sequences.

x1(n) = {1,2,-1,0,3}        x2(n) = { 1,2,-1}

Z{ x1(n) * x2(n)} = X1(z) . X2(z)

X1(z) = 1 + 2z-1 – z-2 + 3 z-4

X2(z) = 1 + 2z-1 – z-2 

(1 + 2z-1 – z-2 + 3 z-4  )  (1 + 2z-1 – z-2  )

= 1 + 4z-1 + 2z-2 – 4 z- 3 + 4 z-4 + 6 z- 5 – 3 z-6 

5)Determine the z-transform of the signal

 x(n ) = rn (sin w0n ) u(n)

Z{(sin w0n ) u(n)}  = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2

Z{ an x(n)} = X(a-1 z)

Therefore

Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2  

= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2

6)Determine the signal x(n) whose z-transform is given by

X(z) = log(1- az-1).

X(z)= log(1-az-1)

Differentiating both sides we get

d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1

-z d/dz { X(z)} = -az-1/1-az-1

= -az-1[ 1/1-az-1]

= -a Z[ a n-1 u(n-1)]                           -------- (1)

From differentiation property

Z{ n x(n)} = -z d/dz [ X(z)]            ------- (2)

Comparing (1) and (2) we get

n  x(n) = -a [ a n-1 u(n-1)]

or x(n) = -a [a n-1 u(n-1)]/n

7)Determine the z-transform of the signal  

x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)

=½ n2 (1/3) n-1 u(n-1) +1/2 n (1/3) n-1 u(n-1)

We know that

Z[(1/3) n u(n)] = z/ z-1/3

Using time-shifting property

Z{(1/3) n-1 u(n-1)] = 1/ z- 1/3

Z [ n (1/3) n-1 u(n-1)] = -z d/dz [1/z-(1/3)]

=-z d/dz( 1/z-1/3)= -z [-1/(z-1/3) 2]= z/ (z-1/3)2

Z [ n2 (1/3) u(n-1)] = -z d/dz [ z/(z-1/3)2]

= z(z+1/3)/(z-1/3)2 

= -z [ (z-1/3)2 -2z(z-1/3)/(z-1/3)4

= z(z+1/3)/(z-1/3)3 

X(z) = ½[z(z+1/3)/(z-1/3)3 + z/ (z-1/3)2]

= z2/(z-1/3)3

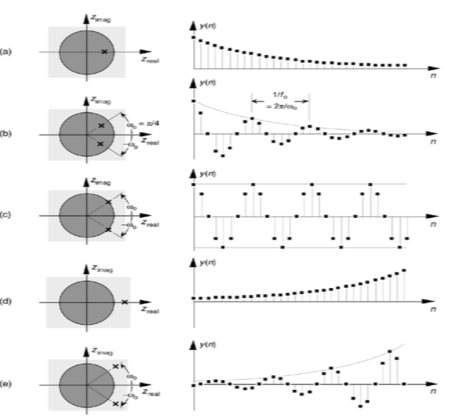
One of the most important characteristics of the z-plane is that the region of filter stability is mapped to the inside of the unit circle on the z-plane. Given the H(z) transfer function of a digital filter, we can examine that function's pole locations to determine filter stability. If all poles are located inside the unit circle, the filter will be stable. On the other hand, if any pole is located outside the unit circle, the filter will be unstable.

Fig1 Various H(z) pole locations and their discrete time domain impulse responses

Figure above shows the z-plane pole locations of several example z-domain transfer functions and their corresponding discrete time-domain impulse responses. The y(n) outputs in Figures (d) and (e) show examples of how unstable filter outputs increase in amplitude, as time passes, whenever their x(n) inputs are nonzero. To avoid this situation, any IIR digital filter that we design should have an H(z) transfer function with all of its individual poles inside the unit circle. 

Key takeaway

The location pole can determine the systems stability.

Examples

Find the z-transform for the sequence

 x[n] = 2 + 3 + 5 + 2

 Solution:

          X(z) = 2 + 3 z-1 + 5 z -2 + 2 z -3   

 If X(z)= 4 – 5 z-2 + z-3 – 2z -4    then find x[n]

 Solution:

 x[n] = 4 - 5 + - 2

Find the z-transform and ROC of the signal

 x(n) = an u(n)

 Solution: 

  X(z) = 

         = an u(n) -----(1)    u(n) = 0 for n<0

          1 for n≥0

  = an ------- (2)

 = n   ------- (3)

 This is a geometric series of infinite length that is

 a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1

          Then from equation (3) it converges when |az-1| < 1 or |z| >|a|

 Therefore

 X(z) = 1/ 1-az-1:  ROC    |z| > |a|

Fig 2 ROC |z|>|a|

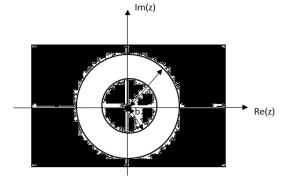
Find the z-transform of the signal x(n) =-b n u(-n-1). Find ROC

X(z) = 

  X(z) =  bn u(-n-1)                                                                   u(-n-1) =0 for n ≥0

            = 1 for n ≤ -1

= bn   = b-1  =

= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1                                                               |z| < |b|

Fig 3 ROC |z|<|b|

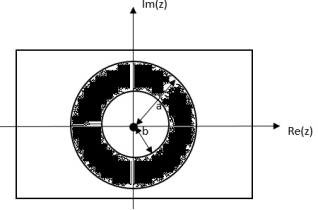
Find the z-transform of x(n) = an u(n) – bn u(-n-1)

 X(z) = 

=  n  + b-1

= z/z-a + z/z-b       ROC |a| < |z| < |b|

Fig 4 ROC |a| < |z| < |b|

|b|< |a|

Fig 5 ROC |b|< |a|

|b| >|a|

Find the z-transform of x(n) = {1,2,3,2}

Given x(0) = 1  x(1) =2   x(2) =3    x(3) = 2

X(z) = 

X(z) = 1+ 2z-1 + 3 z-2 +2 z-3 

Formal inverse z-transform is based on a Cauchy integral

• Less formal ways sufficient most of the time – Inspection method – Partial fraction expansion – Power series expansion

• Inspection Method – Make use of known z-transform pairs such as

anu[n]  1/ (1-az-1)   |z|  >  |a|

Power series method

The z-transform of the sequence x(n) is given by

 gives the expansion in power series form. From power series we get the following sequence:

 x(n) = {∙∙∙∙∙∙∙∙∙∙x(−2), x(−1), x(0), x(1), x(2), ∙∙∙∙∙∙∙∙∙∙∙}

 It is possible to get the power series expansion directly or by long division. In power series expansion technique ROC has a vital role.

Partial fraction expansion method

Find the partial fraction method of

X(z) = ¼ z-1

  (1 – ½ z-1)(1-1/4 z-1)

X(z) =         A                +          B

      Z           (1-1/2z-1)      (1 – ¼ z-1)

By solving A= 1 and B=-1

Therefore,

X(z) =   z     -       z 

 z-1/2 z-1/4

x(n) = (1/2) n u(n) – (1/4) n u(n)

Find the partial fraction of

X(z) =           1

  1+ z-1 + z-2

X(z) =      z

    z2 + z + 1

=                    z

       (z + 0.5 +j 0.866)(z+0.5 – j0.866)

X(z)    =      c                      +                      c* 

  z    z-(-0.5 +j0.866)  z – (- 0. 5 – j 0.866)

X(z)    =      0.5+j0.288                      +          0.5 – j 0.288 

  z    z-(-0.5 +j0.866)            z – (- 0. 5 – j 0.866)

X(z)  =       0.5+j0.288  z                    +          0.5 – j 0.288  z

     z-(-0.5 +j0.866)              z – (- 0. 5 – j 0.866)

By taking inverse z-transform both sides we get

= (0.5+j0.288)( (-0.5 +j0.866) n u(n) +(0.5+j0.288)( (-0.5 -j0.866) n u(n)

Solution of difference equations using Z transform

Z transform converts the difference into algebraic equation in z-domain.

Find the impulse response and step response for the following systems:

y(n) = -  ¾ y(n-1) + 1/8 y(n-2) = x(n)

y(n)  - ¾ y(n-1) + 1/8 y(n-2) = x(n)

Taking z-transform on both sides we get

Y(z) – ¾ [ z-1 Y(z) + y(-1) ] +1/8 [ z-2 Y(z) + z-1 y(-1)+y(-2)] = X(z)

Substituting y(-1)=y(-2)= 0

Y(z) -3/4 z-1 Y(z) + 1/8 z-2 Y(z) = X(z)

Y(z) =     1____________

               1-¾ z-1 + 1/8 z-2

Impulse response

x(n) =        X(z) =1

Y(z) =            1____________           =      1____________ 

                 1-¾ z-1 + 1/8 z-2                          1-  ¾ z-1 + 1/8 z-2  

Y(z)  =  z__________       =        A___        +    B__

X(z)  (z-1/2)(z-1/4)  (z-1/2)   (z-1/4)

By solving A=2 and B=-1.

Y(z) = 2 z          -       z

           z-1/2       (z-1/4)

y(n) = 2 (1/2)n u(n) – (1/4) n u(n).

Step Response

x(n) = u(n) X(z) = z/z-1

Y(z)  =         1_______

X(z)   1-3/4 z-1 + 1/8 z-2

Y(z) = z    +              z2___________

 z-1  z2 -3/4 z +1/8

Y(z)   =    z2___________

z     z2 -3/4 z +1/8

Y(z)   =    z2___________

z     (z-1)(z-1/2)(z-3/4)

=               A       +     B   +      C

          z-1        z-1/2      z- 1/4

By solving A=8/3   B= -2  C= 1/3

Therefore

Y(z) = 8 . z      -2  z   + 1/3 z

 3     z-1      z-1/2 z-1/4

y(n) = 8/3 u(n) – 2(1/2)n u(n) +1/3 (1/4) n u(n)

Key takeaway

The methods used for finding inverse z-transform are partial fraction method and power series method.