Unit - 4
Digital Protection
Development of computer relaying
Since the Digital computer started performing Power system relaying functions, the field of computer relaying has always been evolving. The short circuit, load flow, and stability problems started replacing the DC boards and the Network Analyzers in 1960’s. Systematically, the traditional tools of analytical power engineering were replaced with digital computers.
The evolution of computers over the years has been so rapid that algorithmic sophistication demanded by the relaying programs has finally found a correspondence in the speed and economy of the modern microcomputer; so that at present computer relays offer the best economic and technical solution to the protection problems – in many instances the only workable solution. Indeed, we are at the start of an era in which computer relaying has become routine, and it has further influenced the development of effective tools for real-time monitoring and control of power systems.
Historical Background
Some of the earliest research papers in 1960’s explored the idea that that relaying of all the equipment in a substation would be handled by a single computer. This was justified as the computers at that time were too expensive and the use of multiple computers for digital protection was not economically viable. Hence, the trend to use conventional relays without digital protection seemed to be cost effective. In addition, the speed of contemporary computers was too slow to handle high speed relaying, while the power consumption of the computers was too high. Despite all this, the idea behind digital computer relaying was viewed with great interest as it explored several protection algorithmic details thoroughly.
Several other papers were published at approximately the same time, and led to the algorithmic development for protection of high voltage transmission lines. It was recognized early that transmission line protection function (distance relaying in particular) – more than any other – is of greatest interest to relay engineers because of its widespread use on power systems, its relatively high cost, and its functional complexity. These early researchers began a study of distance protection algorithms which continues unabated to this day.
An entirely different approach to distance relaying has been proposed during recent years. It is based upon the utilization of traveling waves initiated by a fault to estimate the fault distance. Traveling wave relays require relatively high frequencies for sampling voltage and current input signals. Although traveling wave relays have not offered compelling advantages over other relaying principles in terms of speed and accuracy of performance, they have been applied in a few instances around the world with satisfactory performance.
Significant advances in computer hardware had taken place since those early days. The size, power consumption, and cost of computers has gone down significantly while simultaneously the speed of computation has increased by several orders. The appearance of 32 bit microprocessors and computers based upon them make high speed computer relaying technically achievable, while at the same time cost of computer based relays began to become comparable to that of conventional relays.
With reasonable prospects of having affordable computer relays which can be dedicated to a single protection function, attention soon turned to the opportunities offered by computer relays to integrate them into a substation-wide, perhaps even a system-wide, network using high-speed wide-band communication networks.
Expected benefits of computer relaying
- Cost- The cost of a relay is the main consideration in its acceptability. In the early stages of computer relaying, computer relay costs were 10 to 20 times greater than the cost of conventional relays. Over the years, the cost of digital computers has steadily declined; at the same time their computational power has increased substantially.
2. Self-checking and reliability - A computer relay can be programmed to monitor several of its hardware and software subsystems continuously, thus detecting any malfunctions that may occur. It can be designed to fail in a safe mode – i.e. take itself out of service if a failure is detected – and send a service request alarm to the system center. This feature of computer relays is perhaps the most telling technical argument in favor of computer relaying.
3. System integration and digital environment - Digital computers and digital technology have become the basis of most systems in substations. Measurements, communication, telemetry and control are all computer based functions. Many of the power transducers (current and voltage transformers) are in the process of becoming digital systems. Fiber optic links, because of their immunity to Electromagnetic Interference (EMI), are likely to become the medium of signal transmission from one point to another in a substation; it is a technology particularly suited to the digital environment. In substations of the future, computer relays will fit in very naturally. They can accept digital signals obtained from newer transducers and fiber optic channels, and become integrated with the computer based control and monitoring systems of a substation.
4. Functional flexibility and adaptive relaying - Since the digital computer can be programmed to perform several functions as long as it has the input and output signals needed for those functions, it is a simple matter to the relay computer to do many other substation tasks. For example, measuring and monitoring flows and voltages in transformers and transmission lines, controlling the opening and closing of circuit breakers and switches, providing backup for other devices that have failed, are all functions that can be taken over by the relay computer. The relaying function calls for intensive computational activity when a fault occurs on the system. This intense activity at best occupies the relaying computer for a very small fraction of its service life – less than a tenth of a percent. The relaying computer can thus take over these other tasks at practically no extra cost.
Computer relay architecture
Computer relays consist of subsystems with well defined functions. Although a specific relay may be different in some of its details, these subsystems are most likely to be incorporated in its design in some form.
The block diagram below shows the principal subsystems of a computer relay. The processor is central to its organization. It is responsible for the execution of relay programs, maintenance of various timing functions, and communicating with its peripheral equipment. Several types of memories shown below – each of them serves a specific need.
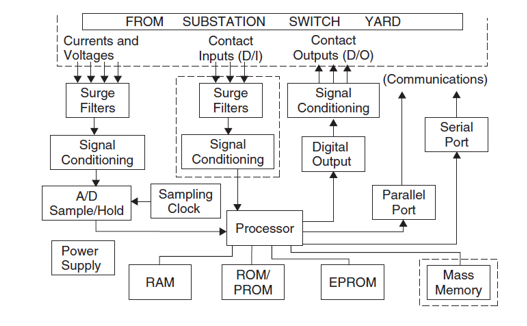
Each of them serves a specific need. The Random Access Memory (RAM) holds the input sample data as they are brought in and processed. It may also be used to buffer data for later storage in a more permanent medium. In addition, RAM is needed as a scratch pad to be used during relay algorithm execution. The Read Only Memory (ROM) or Programmable Read Only Memory (PROM) is used to store the programs permanently. In some cases the programs may execute directly from the ROM, if its read time is short enough. If this is not the case, the programs must be copied from the ROM into the RAM during an initialization stage, and then the real-time execution would take place from the RAM. The Erasable PROM (EPROM) is needed for storing certain parameters (such as the relay settings) which may be changed from time to time, but once set must remain fixed, even if the power supply to the computer is interrupted. Either a core type memory or an on-board battery backed RAM may be suitable for this function.
A large capacity EPROM is likely to become a desirable feature of a computer relay. Such a memory would be useful as an archival data storage medium, for storing fault related data tables, time-tagged event logs, and audit trails of interrogations and setting changes made in the relay. The main consideration here is the cost of such a memory. The memory costs have dropped sufficiently by now so that archival storage of oscillography and sequence-of-event data on a large scale within the relays has become possible.
Many of the input signals such as phase voltages and currents encountered in power systems are essentially periodic. Ideally, the voltages and currents present in the system in steady state are pure sinusoids at the power system frequency. Some devices (for example, power transformers, inverters, converters and loads) create harmonic distortion in the steady state signals. The signals seen by protective relays also fail to be pure sinusoids. The non-fundamental frequency content of the voltage and current seen by a relay are not truly periodic but change in time.
The nature of these non-fundamental frequency signals has an important bearing on the performance of relaying algorithms. The Fourier series provides a technique for examining these signals and determining their harmonic content.
A signal r(t) is said to be periodic if there is a T such that
r(t) = r(t + T); for all t …..(1)
If r(t) is periodic and not a constant then let T0 be the smallest positive value of T for which Equation 1 is satisfied. The period T0 is called the fundamental period of r(t). If r(t) = sin(ω0t) then equation 1 is satisfied for:
T =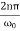 
; n = 1,2,3….
The smallest positive value is, of course, T = 2π/ω0. Associated with the fundamental
Period is a fundamental frequency defined by: ω0 =2π/T0 .
The objective of Fourier analysis is to decompose an arbitrary periodic signal into components as in equation 2:
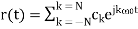……(2)
Exponential Fourier series
Given a periodic signal with fundamental frequency ω0 the exponential Fourier series is written as:
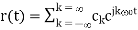……(1)
The task is to determine the coefficients ck. An important property of the exponentials makes the calculation a simple process. Note that:
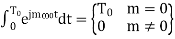….(2)
The value of the integral is clear for m = 0, while for m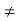 
0
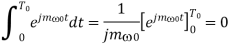
Since ω0T0 = 2π
To compute the Fourier series coefficients it is only necessary to multiply Equation (1) by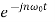 
and integrate over a period:
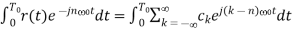
From Equation (2) every term on the right hand side vanishes except the nth, term yielding:
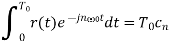
Or
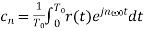……….(3)
Equation (3) can be evaluated over any period that is convenient
Sine and Cosine Fourier series
Through the use of the Euler identity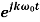 
= cos(kωot) + j sin(kωot)
It is possible to write the exponential series in terms of sines and cosines
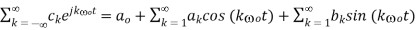….(1)
Where
ao = co
ak = ck + c−k k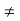 
0
bk = j(ck − c−k) k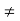 
0
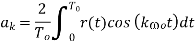
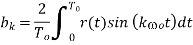
The real and even signals have expansions of the form of Equation (1) with only cosine terms, while real and odd signals have such expansions with only sine terms.
If the Fourier series is written as
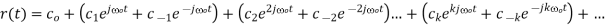
The various terms can be recognized as
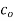the dc component (average value)
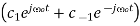the fundamental frequency component
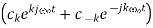kth harmonic
Properties of Fourier Transform:
Linearity property
If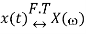 
And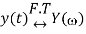 
Then linearity property states that
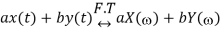
Time shifting property
If 
Then Time shifting property states that
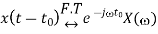
Frequency Shifting property
If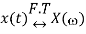 
Then frequency shifting property states that
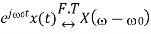
Time Reversal Property
If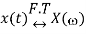 
The time reversal property states that
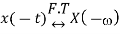
Time Scaling Property
If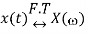 
Then Time scaling property states that
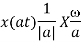
Differentiation and Integration properties
If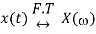 
Then Differentiation property states that
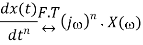
And integration property states that
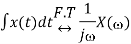
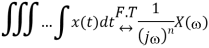
Multiplication and convolution properties
If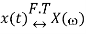 
And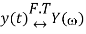 
Then multiplication property states that
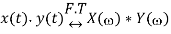
And convolution property states that
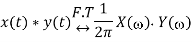
A sinusoid x(t) with frequency kf0 with a Fourier series
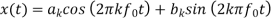
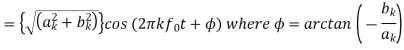
Has a phasor representation
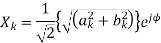
Where the square root of 2 in the denominator is to obtain the rms value of the sinusoid. The phasor in complex form becomes:
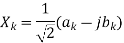
Using the relationship of the Fourier series coefficients with the DFT, the phasor representation of the kth harmonic component is given by
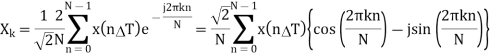
Using the notation x(nΔT) = xn, and 2π/N = θ (θ is the sampling angle measured in terms of the period of the fundamental frequency component)
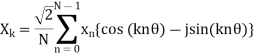
If we define the cosine and sine sums as follows:
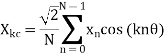
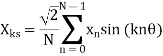
Then, the phasor Xk is given by:
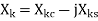
Sampled data from input signals are the starting point of digital signal processing. The computation of phasors of voltages and currents begins with the samples of the waveform taken at uniform intervals kΔT (k = 0, ±1, ±2, ±3, ±4,…}. Consider an input signal x(t) which is being sampled, yielding sampled data x(kΔT). We may view the sampled data as a time function x′(t) consisting of uniformly spaced impulses, each with a magnitude x(kΔT).
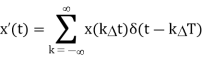
The sampled data function is a product of the function x(t) and the sampling function δ(t − kΔT). The Fourier transform X′(f) of x′(t) is the convolution of the Fourier transforms of x(t) and of the unit impulse train.
The Fourier transform of the impulse train is:
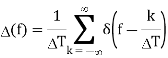
Hence, the Fourier transform of the sampled data function is the convolution of Δ(f) and X(f):
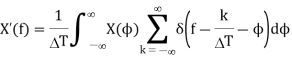
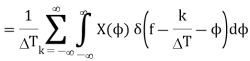
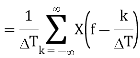
The Fourier transform of x(t) is shown to be band-limited, meaning that it has no components beyond a cutoff frequency fc. The sampled data have a Fourier transform, which consist of an infinite train of the Fourier transforms of x(t) centered at frequency intervals of (k/ΔT) for all k.
If the cutoff frequency fc is greater than one-half of the sampling frequency fs, the Fourier transform of the sampled data will be as shown in figure below. In this case, the spectrum of the sampled data is different from that of the input signal in the region, where the neighboring spectra overlap as shown by the shaded region in figure. This implies that frequency components estimated from the sampled data in this region will be in error, due to a phenomenon known as aliasing.
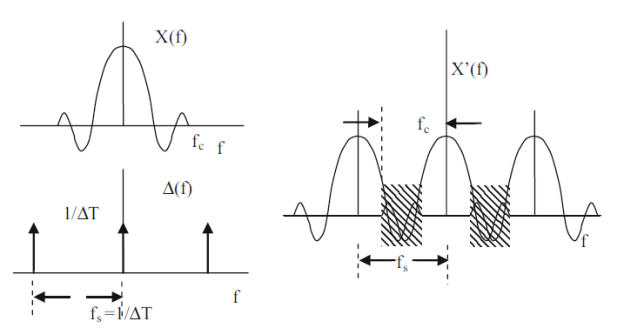
Figure- Fourier transform of the sampled data function when the input signal is band-limited to a frequency greater than half of the sampling frequency. The estimate of frequencies from sampled data in the shaded region will be in error because of aliasing.
References:
1. J. L. Blackburn, “Protective Relaying: Principles and Applications”, Marcel Dekker, New York, 1987.
2. Y.G. Paithankar and S. R. Bhide, “Fundamentals of power system protection”, Prentice Hall, India, 2010.
3. A.G. Phadke and J. S. Thorp, “Computer Relaying for Power Systems”, John Wiley & Sons, 1988.
4. A.G. Phadke and J. S. Thorp, “Synchronized Phasor Measurements and their Applications”, Springer, 2008.
5. D. Reimert, “Protective Relaying for Power Generation Systems”, Taylor and Francis, 2006.
