Unit 5
Two Port Network and Network Functions
The parameters of a two- port network is called as two port network parameters. The types are: -
- Z parameters
- Y parameters
- T parameters
- T’ parameters
- h-parameters
- g-parameters
Z parameters:
The following set of two equations by considering variables V1 & V2 as dependent and I1 & I2 as independent. The coefficients of independent variables, I1 and I2 are called as Z parameters.
V1 = Z11 I1 + Z12 I2
V2 = Z21 I1 + Z22 I2
The Z parameters are:
Z11 = V1 I1 when I2 =0
Z12 = V1 I2 when I1=0
Z21= V2I1 when I2 =0
Z22 = V2I1 when I2 =0
The Z parameters are called as impedance parameters because these are the ratio of volatges and currents.
To calculate Z11 and Z21 by doing open circuit of port2. Similiarly the other two parameters Z12 and Z22 are calculated by doing open circuit of port1.
Y parameters:
The set of equations can be obtained by considering I1 and I2 as dependent and V1 and V2 as independent. The co-effecients of independent variables V1 and V2 are called as Y parameters.
I1 = Y11 V1 + Y12 V2
I2 = Y21 V1 + Y22 V2
Y parameters are called as admittance parameters because these are simply, the ratios of currents and voltages. Units of Y parameters are mho.
T parameters:
The set of equations can be obtained by considering V1 and I1 as dependent and V2 and I2 as independent. The coefficients V2 and I2 are called as T parameters.
V1 = A V2 – B I2
I1 = C V2 – D I2
The T parameters are :
A = V1/V2 when I2 =0
B = -V1 / I2 when V2 =0
C = I1/V2 when I2 =0
D = -I1/I2 when V2 =0
h- parameters
The following set of two equations by considering the variables V1 and I2 as dependent and I1 and V2 as independent. The coefficient of independent variables I1 and V2 are called as h-parameters.
V1 = h11 I1 + h12 V2
I2 = h21 I1 + h22 V2
The h parameters are:
h 11 = V1/I1 when V2 =0
h 12 = V1 / V2 when I1=0
h21 = I2/I1 when V2 =0
h22 = I2/V2 when I1 =0
h-parameters are called as hybrid parameters. The parameters, h12 and h21, do not have any units, since those are dimension-less. The units of parameters, h11 and h22, are Ohm and Mho respectively.
g-parameters
The following set of two equations can be obtained by considering the variables I1 & V2 as dependent and V1 & I2 as independent. The coefficients of independent variables, V1 and I2 are called as g-parameters.
I1=g11V1+g12I2I1
V2=g21V1+g22I2
The g-parameters are
g11=I1V1, whenI2=0
g12=I1I2, whenV1=0
g21=V2V1, whenI2=0
g22=V2I2, whenV1=0
g-parameters are called as inverse hybrid parameters.
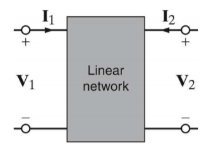
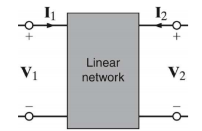
A two-port network requires two terminal pairs (total 4 terminals). Two voltages and two currents are shown and two are independently specified.
Input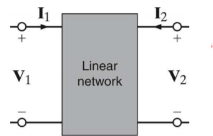 
Output
By convention, regard Port 1 as Input and Port 2 as Output.
C 4 2 = (4/2) = 4!/ 2! (4-2)! = 24 / 2 x 2 = 6.
Finding the model parameters
For each of the four types of models, the four parameters can be found from variables V1, V2 , I1,I2 network by the following.
- For Z-model:
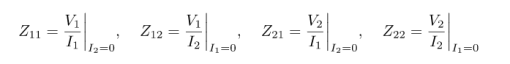
- For Y-model:
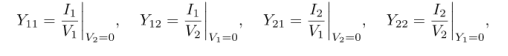
- For A-model
- For H model
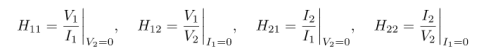
Find the Z-model and Y-model of the circuit
First assume I2 , we get
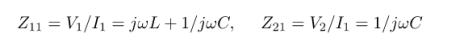
Assume I1 =0 we get
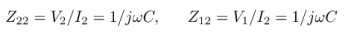
The parameters of the Y-model can be found as the inverse of :
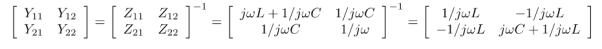
Combinations of two-port models
- Series connection of two 2-port networks:
- Parallel connection of two 2-port networks:
- Cascade connection of two 2-port networks:
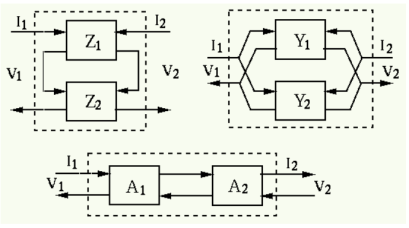
The circuit shown below contains a two-port network represented by a Z-model:
The input voltage is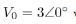 
with an internal impedance 
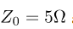and the load impedance is 
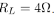. Find the two voltages V1, V2 and two currents I1 , I2 
.
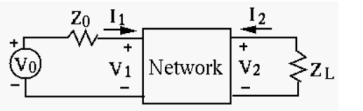
First according to Z-model we have
V1 = Z11 I1 + Z 12 I 2 = 4 I1 + j 3 I2
V2 = Z21 I1 + Z22 I2 = j 3I1 + 2 I2
Second two more equations can be obtained from the circuit.
V1 = Vo – Zo I1 = 3 – 5 I1
V2 = -ZL I2 = -4I2
Substituting the last two equations for V1 and V2 into the first two we get
9 I1 + j 3 I2 = 3
j 3 I1 + 6 I 2 =0
Solving we get
I1 = 2/7 , I2 = -j/7 , V1 =11/7 , V2 = j4/7
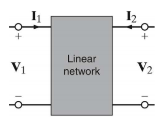
[V1] = [Z11 Z12][I1]
[V2] =[ Z21 Z22] [I2]
V1 = Z11 I1 + Z12 I2
V2 = Z21 I1 + Z22 I2
Determine Z parameters
Z11 = V1/I1 |I2 =0 open circuit input impedance
Z22 = V2/I2 |I1 =0 Open circuit output impedance
Z12 = V1/I2 | I1 =0
Z21 = V2/I1 |I2 =0
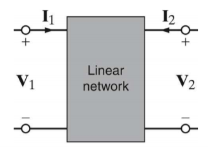
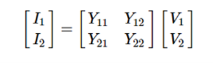
I1 = Y11 V1 + Y 12 V2
I 2 = Y21 V1 + Y 22 V2
To determine Y parameters:
y11 = I1/V1 |V2=0 ----- short circuit input admittance
y22 = I2/V2 |V1=0 ---- short circuit output admittance
y12 = I1/V2 |v1=0
y21 = I2/V1 |v2=0 trans admittance
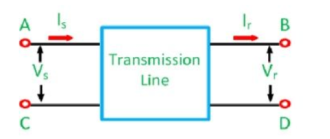
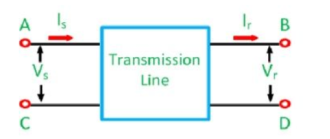
The voltage and current in the output and input terminals of a two-port network are given by the equations shown below
Vs = A Vr + B Ir
Is = C Vr + D Ir
Vs = sending end voltage
Is = sending end current
Vr = receiving end voltage
Ir = receiving end current
A, B, C and D are the constants also known as the transmission parameters or chain parameters. These parameters are used for the analysis of an electrical network.
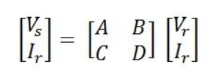
For open circuit
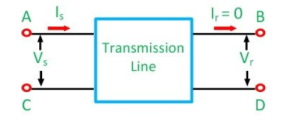
In the open circuit, the output terminals are open, and the voltage measure across them is Vr. Since the circuit is open at the receiving end, the current Ir remains zero.
Vs = A Vr + B0
Vs = A Vr +0
A = Vs/Vr | Ir =0
From above equations, we get the value of A parameter which is the ratio of sending end voltage to the receiving end voltage.
Similarly, if Ir =0 is substituted in current equation,
Is = CVr + D0
Is = CVr +0
C = Is/Vr | Ir =0
we get the value of c parameter which is the ratio of the sending end voltage to the current. Its unit is Siemens.
For short circuit
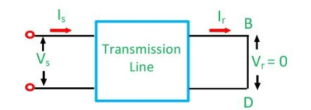
For the short circuit, the voltage remains zero at the receiving end.
Vs = A0 + B Ir
Vs = 0 + B Ir
B = Vs/Ir | Vr=0
If we put Vr = 0 in the equation, we get the value of B which is the ratio of sending end voltage to the receiving end currents. Its unit is ohms.
Similarly, if we put Vr= 0 in current equations,
Is = C0 + D Ir
Is = 0 + D Ir
D = Is/ Ir | Vr =0
We get the value of D, which is the ratio of the sending current to the receiving current. It is the dimensionless constant.
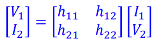
h 1 1 = V 1 / I1 when V2 =0
h 1 2 = V1/ V2 when I1 =0
h 21= I2/I1 when V2=0
h22 = I2/V2 when I1 =0
References:
- Network theory by A.V Bakshi, U.A Bakshi
- Network Theory Analysis and Synthesis by Smarajit Ghosh
- Networks: An introduction by Mark Newman
- Network Theory (Bput) book by Satpathy
Unit 5
Two Port Network and Network Functions
The parameters of a two- port network is called as two port network parameters. The types are: -
- Z parameters
- Y parameters
- T parameters
- T’ parameters
- h-parameters
- g-parameters
Z parameters:
The following set of two equations by considering variables V1 & V2 as dependent and I1 & I2 as independent. The coefficients of independent variables, I1 and I2 are called as Z parameters.
V1 = Z11 I1 + Z12 I2
V2 = Z21 I1 + Z22 I2
The Z parameters are:
Z11 = V1 I1 when I2 =0
Z12 = V1 I2 when I1=0
Z21= V2I1 when I2 =0
Z22 = V2I1 when I2 =0
The Z parameters are called as impedance parameters because these are the ratio of volatges and currents.
To calculate Z11 and Z21 by doing open circuit of port2. Similiarly the other two parameters Z12 and Z22 are calculated by doing open circuit of port1.
Y parameters:
The set of equations can be obtained by considering I1 and I2 as dependent and V1 and V2 as independent. The co-effecients of independent variables V1 and V2 are called as Y parameters.
I1 = Y11 V1 + Y12 V2
I2 = Y21 V1 + Y22 V2
Y parameters are called as admittance parameters because these are simply, the ratios of currents and voltages. Units of Y parameters are mho.
T parameters:
The set of equations can be obtained by considering V1 and I1 as dependent and V2 and I2 as independent. The coefficients V2 and I2 are called as T parameters.
V1 = A V2 – B I2
I1 = C V2 – D I2
The T parameters are :
A = V1/V2 when I2 =0
B = -V1 / I2 when V2 =0
C = I1/V2 when I2 =0
D = -I1/I2 when V2 =0
h- parameters
The following set of two equations by considering the variables V1 and I2 as dependent and I1 and V2 as independent. The coefficient of independent variables I1 and V2 are called as h-parameters.
V1 = h11 I1 + h12 V2
I2 = h21 I1 + h22 V2
The h parameters are:
h 11 = V1/I1 when V2 =0
h 12 = V1 / V2 when I1=0
h21 = I2/I1 when V2 =0
h22 = I2/V2 when I1 =0
h-parameters are called as hybrid parameters. The parameters, h12 and h21, do not have any units, since those are dimension-less. The units of parameters, h11 and h22, are Ohm and Mho respectively.
g-parameters
The following set of two equations can be obtained by considering the variables I1 & V2 as dependent and V1 & I2 as independent. The coefficients of independent variables, V1 and I2 are called as g-parameters.
I1=g11V1+g12I2I1
V2=g21V1+g22I2
The g-parameters are
g11=I1V1, whenI2=0
g12=I1I2, whenV1=0
g21=V2V1, whenI2=0
g22=V2I2, whenV1=0
g-parameters are called as inverse hybrid parameters.
A two-port network requires two terminal pairs (total 4 terminals). Two voltages and two currents are shown and two are independently specified.
Input 
Output
By convention, regard Port 1 as Input and Port 2 as Output.
C 4 2 = (4/2) = 4!/ 2! (4-2)! = 24 / 2 x 2 = 6.
Finding the model parameters
For each of the four types of models, the four parameters can be found from variables V1, V2 , I1,I2 network by the following.
- For Z-model:
- For Y-model:
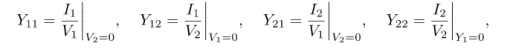
- For A-model
- For H model
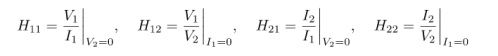
Find the Z-model and Y-model of the circuit
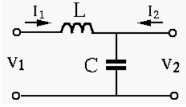
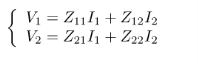
First assume I2 , we get
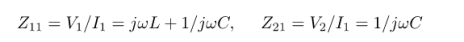
Assume I1 =0 we get
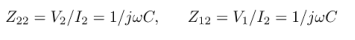
The parameters of the Y-model can be found as the inverse of :
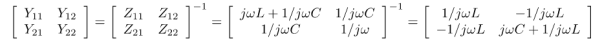
Combinations of two-port models
- Series connection of two 2-port networks:
- Parallel connection of two 2-port networks:
- Cascade connection of two 2-port networks:
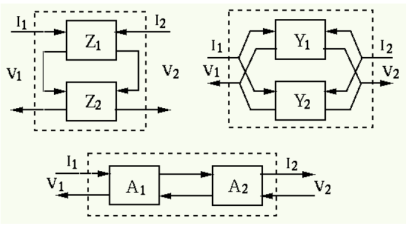
The circuit shown below contains a two-port network represented by a Z-model:
The input voltage is 
with an internal impedance 
and the load impedance is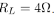 
. Find the two voltages V1, V2 and two currents I1 , I2 
.
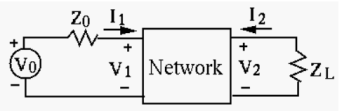
First according to Z-model we have
V1 = Z11 I1 + Z 12 I 2 = 4 I1 + j 3 I2
V2 = Z21 I1 + Z22 I2 = j 3I1 + 2 I2
Second two more equations can be obtained from the circuit.
V1 = Vo – Zo I1 = 3 – 5 I1
V2 = -ZL I2 = -4I2
Substituting the last two equations for V1 and V2 into the first two we get
9 I1 + j 3 I2 = 3
j 3 I1 + 6 I 2 =0
Solving we get
I1 = 2/7 , I2 = -j/7 , V1 =11/7 , V2 = j4/7
[V1] = [Z11 Z12][I1]
[V2] =[ Z21 Z22] [I2]
V1 = Z11 I1 + Z12 I2
V2 = Z21 I1 + Z22 I2
Determine Z parameters
Z11 = V1/I1 |I2 =0 open circuit input impedance
Z22 = V2/I2 |I1 =0 Open circuit output impedance
Z12 = V1/I2 | I1 =0
Z21 = V2/I1 |I2 =0
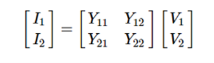
I1 = Y11 V1 + Y 12 V2
I 2 = Y21 V1 + Y 22 V2
To determine Y parameters:
y11 = I1/V1 |V2=0 ----- short circuit input admittance
y22 = I2/V2 |V1=0 ---- short circuit output admittance
y12 = I1/V2 |v1=0
y21 = I2/V1 |v2=0 trans admittance
The voltage and current in the output and input terminals of a two-port network are given by the equations shown below
Vs = A Vr + B Ir
Is = C Vr + D Ir
Vs = sending end voltage
Is = sending end current
Vr = receiving end voltage
Ir = receiving end current
A, B, C and D are the constants also known as the transmission parameters or chain parameters. These parameters are used for the analysis of an electrical network.
For open circuit
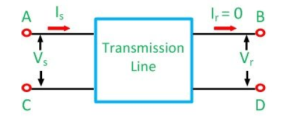
In the open circuit, the output terminals are open, and the voltage measure across them is Vr. Since the circuit is open at the receiving end, the current Ir remains zero.
Vs = A Vr + B0
Vs = A Vr +0
A = Vs/Vr | Ir =0
From above equations, we get the value of A parameter which is the ratio of sending end voltage to the receiving end voltage.
Similarly, if Ir =0 is substituted in current equation,
Is = CVr + D0
Is = CVr +0
C = Is/Vr | Ir =0
we get the value of c parameter which is the ratio of the sending end voltage to the current. Its unit is Siemens.
For short circuit
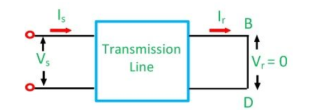
For the short circuit, the voltage remains zero at the receiving end.
Vs = A0 + B Ir
Vs = 0 + B Ir
B = Vs/Ir | Vr=0
If we put Vr = 0 in the equation, we get the value of B which is the ratio of sending end voltage to the receiving end currents. Its unit is ohms.
Similarly, if we put Vr= 0 in current equations,
Is = C0 + D Ir
Is = 0 + D Ir
D = Is/ Ir | Vr =0
We get the value of D, which is the ratio of the sending current to the receiving current. It is the dimensionless constant.
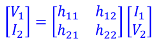
h 1 1 = V 1 / I1 when V2 =0
h 1 2 = V1/ V2 when I1 =0
h 21= I2/I1 when V2=0
h22 = I2/V2 when I1 =0
References:
- Network theory by A.V Bakshi, U.A Bakshi
- Network Theory Analysis and Synthesis by Smarajit Ghosh
- Networks: An introduction by Mark Newman
- Network Theory (Bput) book by Satpathy
