Unit 4
Static Magnetic Fields
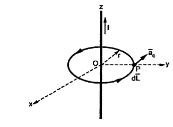
Let us consider a conductor carrying direct current I and a steady magnetic field is produced around it. The law helps us to obtain magnetic field intensity  produced at a point P due to differential current element idL. The current carrying conductor is as shown in the figure.
produced at a point P due to differential current element idL. The current carrying conductor is as shown in the figure.
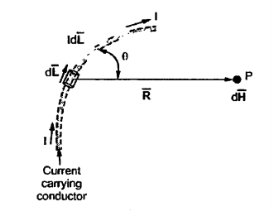
Consider differential length dL and differential current IdL. This is a small part of the current carrying conductor. The point P is at a distance R from differential current element. 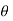 is the angle between the differential current element and the line joining point P to the differential current element?
is the angle between the differential current element and the line joining point P to the differential current element?
Bio-Savart Law states that the magnetic field intensity 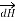 produced at point P due to differential current IdL is,
produced at point P due to differential current IdL is,
Proportional to the product of current I and differential length dL.
The sine of angle between the element and the line joining point P to the element.
Inversely proportional to the square of distance R between point P and the element.
Bio-Savart law can be stated as ,
d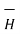 α I dL sin Ɵ / R 2
α I dL sin Ɵ / R 2
d =k I dL sin Ɵ / R 2
=k I dL sin Ɵ / R 2
Where k = constant of proportionality
In SI units, k = 1/ 4 π.
d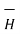 = I dL sin Ɵ / 4πR 2
= I dL sin Ɵ / 4πR 2
In vector form,
Let dL = Magnitude of vector length 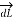 and
and
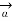 R = Unit vector in the direction from differential current element to point P.
R = Unit vector in the direction from differential current element to point P.
Then from rule of cross product ,
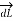 x
x 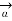 R = dL |
R = dL |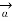 R| sin Ɵ = dL sin Ɵ |
R| sin Ɵ = dL sin Ɵ |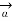 R|=1
R|=1
Replacing we get
d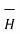 = I d
= I d  x
x  R / 4πR 2 A/m
R / 4πR 2 A/m
 R =
R =  / |
/ |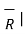 =
=  / R
/ R
d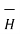 = I d
= I d 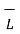 x
x  / 4πR 3 A/m
/ 4πR 3 A/m
This is the mathematical form of Bio-Savarts Law.
According to direction of cross product the direction of 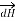 is normal to the plane containing two vectors and the normal direction along the progress of right- handed screw turned from
is normal to the plane containing two vectors and the normal direction along the progress of right- handed screw turned from 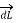 through smaller angle
through smaller angle 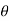 towards the line joining element to point P.
towards the line joining element to point P.
Therefore, direction of 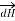 is normal to the plane of paper.
is normal to the plane of paper.
According to right- handed screw rule the direction of 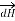 is going into the plane of paper.
is going into the plane of paper.
The entire conductor is made of differential elements . Therefore , in order to obtain the total magnetic field take the integral
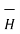 =
= 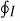 d
d 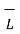 x
x 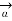 R / 4πR 2
R / 4πR 2
The closed line integral is required to ensure that all the current elements are considered because current can flow only in the closed path provided by close circuit.
If the current element is considered at point 1 and point P at point 2 as shown in the figure, then
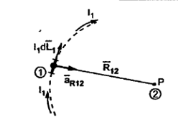
D  2 = I1 d
2 = I1 d  1 x x
1 x x  R 12 / 4πR 2 12
R 12 / 4πR 2 12
Where
I1 = current flowing through dL1 at point 1.
DL1 = Differential vector length at point 1
 R12 = Unit vector in the direction from element at point 1 to point P at point2.
R12 = Unit vector in the direction from element at point 1 to point P at point2.
 R12 =
R12 = 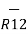 / |
/ |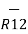 | =
| =  / R12
/ R12
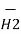 =
=  d
d 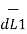 x
x 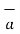 R12 / 4 π R 2 12 A/m
R12 / 4 π R 2 12 A/m
This integral form is called Biot-Savart law.
Problem:
Find the incremental field strength at P2 due to the current element of 2πa2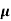 Am at P1. The co-ordinates of P1 and P2 are (4,0,0) and (0,3,0) respectively.
Am at P1. The co-ordinates of P1 and P2 are (4,0,0) and (0,3,0) respectively.
Solution:
The two points P1 and P2 along with the I1dL1 current element at I1 are shown in figure.
According to Bio-Savart law
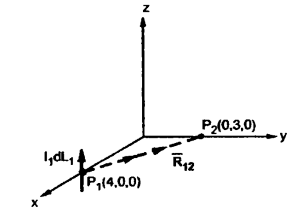
d 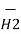 = I1 d
= I1 d 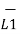 x
x 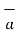 R12 / 4 π R 2 12
R12 / 4 π R 2 12
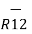 = (0-4)
= (0-4) 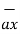 + (3-0) ay + 0. Az
+ (3-0) ay + 0. Az
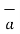 R12 =
R12 = 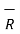 12 /|
12 /|  12 |
12 |
= -4 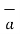 x + 3
x + 3 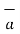 y /
y / 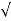 16 + 9
16 + 9
= -4 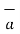 x + 3
x + 3  y /5
y /5
While I1 dL1 = 2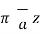
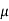 A m.
A m.
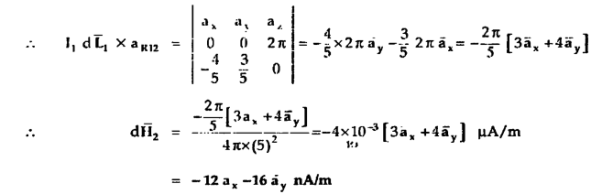
3.3 Ampere ‘s Circuit Law –
Gauss’s Law is useful to obtain  in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
It states that
The line integral of magnetic field intensity  around closed path is exactly equal to direct current enclosed by that path.
around closed path is exactly equal to direct current enclosed by that path.
The mathematical representation of Ampere’s circuital law is
 ---------------------(1)
---------------------(1)
This law is useful to determine  when current distribution is symmetrical.
when current distribution is symmetrical.
Proof:
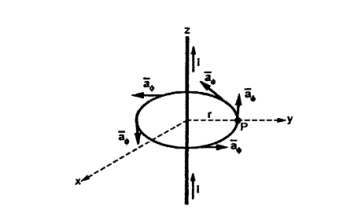
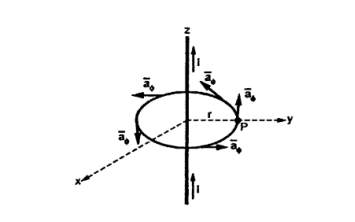
Consider a long straight conductor carrying direct current I placed along z axis as shown in figure. Consider a closed circular path of radius r which encloses the straight conductor carrying direct current I. The point P is at perpendicular distance r from the conductor.
Consider  at point P which is direction
at point P which is direction 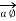 direction tangential to circular path at point P.
direction tangential to circular path at point P.
Therefore,

While 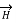 obtained at point P, from Biot-Savart law due to infinitely long conductor is,
obtained at point P, from Biot-Savart law due to infinitely long conductor is,
 = 1/ 2 π r .
= 1/ 2 π r .  ɸ . r dɸ .
ɸ . r dɸ . 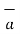 ɸ
ɸ
= 1/ 2  r . dɸ = 1/ 2 π . dɸ
r . dɸ = 1/ 2 π . dɸ
Integrating  .
. 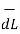 over the entire closed path
over the entire closed path
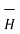 .
. 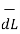 =
= 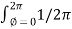 dɸ = 1/ 2 π [ɸ] 0 2π = I. 2 π/ 2 π
dɸ = 1/ 2 π [ɸ] 0 2π = I. 2 π/ 2 π
This proves that the integral 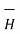 .
.  along closed path gives the direct current enclosed by that closed path.
along closed path gives the direct current enclosed by that closed path.
Steps to Apply Amper’s Circuital Law:
Step1: Consider a closed path preferably symmetrical such that it encloses the direct current I once. This is Amperian path.
Step2: Consider differential length 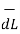 depending upon the co-ordinate system used.
depending upon the co-ordinate system used.
Step3: Identify the symmetry and find in which direction 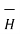 exists according to co-ordinate system used.
exists according to co-ordinate system used.
Step 4: Find 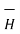 .
. 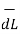 . Make sure that
. Make sure that 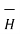 and
and 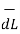 are in the same direction.
are in the same direction.
Step 5: Find the integral of 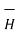 .
.  around the closed path. And equate it to current I enclosed by the path.
around the closed path. And equate it to current I enclosed by the path.
To apply Ampere’s circuital law the following conditions must be satisfied,
- The
 ie either tangential or normal to the path, at each point of the closed path.
ie either tangential or normal to the path, at each point of the closed path. - The magnitude of
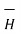 must be same at all points of the path where
must be same at all points of the path where 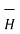 is tangential.
is tangential.
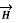 due to straight conductors.
due to straight conductors.
Consider an infinitely long straight conductor which is placed along z-axis carrying direct current I as shown in figure. Consider the Amperian closed path enclosing the conductor as shown in figure. Consider point P on the closed path at which 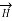 is obtained. The radius of the path is r from the conductor. The magnitude of
is obtained. The radius of the path is r from the conductor. The magnitude of 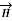 depends on r and the direction is always tangential to the closed path. So,
depends on r and the direction is always tangential to the closed path. So,  has only component in
has only component in 
 direction say H
direction say H  .
.
Consider elementary length  at point P in cylindrical co-ordinates it is r d
at point P in cylindrical co-ordinates it is r d in
in  .
.
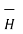 = Hɸ
= Hɸ  ɸ and
ɸ and 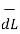 = r dɸ .
= r dɸ . ɸ
ɸ
 .
.  = Hɸ
= Hɸ  ɸ . r dɸ .
ɸ . r dɸ . ɸ = Hɸ r dɸ
ɸ = Hɸ r dɸ
According to Ampere’s circuit law ,
 = I
= I
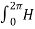 ɸ . r. dɸ = I
ɸ . r. dɸ = I
Hɸ . r  . dɸ = I
. dɸ = I
Hɸ . r [2π] =I
Hɸ = 1/ 2π r
Hence 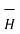 at point P is given by
at point P is given by
 = Hɸ.
= Hɸ.  ɸ = 1/ 2 π r .
ɸ = 1/ 2 π r .  ɸ
ɸ
The total magnetic lines of force that is magnetic flux crossing a unit area in a plane at right angles to the direction of flux is called magnetic flux density. It is denoted  and is vector quantity. It is measured in weber per square metre called as Tesla.
and is vector quantity. It is measured in weber per square metre called as Tesla.
If Vm is the scalar magnetic potential, then it must satisfy the equation
 x
x 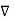 Vm =0
Vm =0
But the scalar magnetic potential is related to the magnetic field intensity 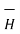 as
as
 = -
= - 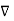 Vm
Vm
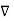 x (-
x (-  =0 that is
=0 that is 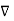 x (
x (  =0
=0
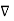 x (
x ( 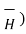 =
= 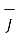 that is
that is 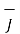 =0
=0
Thus scalar magnetic potential Vm can be defined for source free region where 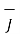 that is the current density is zero.
that is the current density is zero.
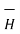 = -
= - 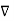 Vm only for
Vm only for 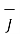 =0
=0
Vector magnetic potential:
The vector magnetic potential is denoted as 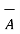 and measured in Wb/m . It has to satisfy equation that divergence of a curl of a vector is always zero.
and measured in Wb/m . It has to satisfy equation that divergence of a curl of a vector is always zero.
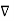 .
. 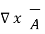 =0
=0
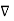 .
. 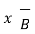 =0
=0
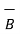 =
= 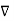
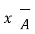
The curl of a vector magnetic potential is the flux density.
Now 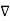 .
. 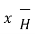 =
= 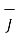

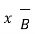 /
/ 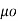 =
= 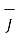
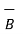 =
= 
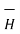

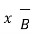 =
= 
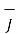
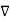 x
x  x A = =
x A = = 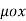
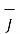
Using vector identity to express on L.H.S we write
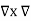
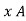 = =
= =  J
J
J = 1/ 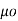 [
[ 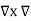
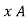 ] = 1/ 1/
] = 1/ 1/ 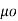 [
[ 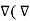 x
x  ) -
) -  2
2 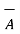 ]
]
Thus if vector magnetic potential is known then current density J can be obtained.
Consider two current carrying conductors placed parallel to each other. Each of these conductors produce its own flux around it. So when such two conductors are placed close to each other there exists a force due to the interaction of two fluxes. The force between such parallel current carrying conductors depends on the directions of the two currents.
If the directions of both the currents are same then the conductors experience a force of attraction. If the direction of two currents are opposite to each other then the conductors experience force of repulsion.
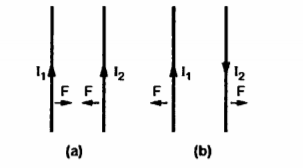
Let us consider two current elements I1 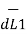 and I2
and I2 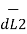 as shown in the figure. As the currents are flowing in the same direction through the elements the force d(
as shown in the figure. As the currents are flowing in the same direction through the elements the force d(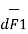 1) exerted on element I1
1) exerted on element I1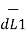 due to magnetic field
due to magnetic field  produced by other element I2
produced by other element I2 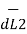 is the force of attraction.
is the force of attraction.
From the equation of force the force exerted on a differential current element is given by
d(d  ) = I1
) = I1 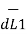 x d
x d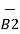
According to Bio-Savart’s law the magnetic field produced by the current element I2 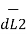 is given by free space
is given by free space
x d =
= 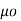 d
d 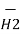 =
= 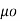 [ I2
[ I2 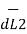 x
x 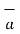 R21 / 4
R21 / 4  R 2 21
R 2 21
Substituting the value of d
d ( d 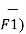 =
=  x I1
x I1 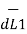 x ( I2
x ( I2 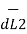 x
x 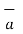 R21 ) / 4
R21 ) / 4 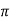 R 2 21
R 2 21
The equation represents force between two current elements.
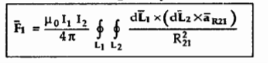
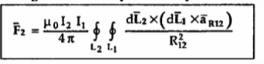
The above equation indicates that the forces F1 and F2 obey Newton’s third law that for every action there is equal and opposite reaction.
For the two current carrying conductors of length l each the force exerted is given by
F = 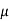 I1 I2 l / 2 π d
I1 I2 l / 2 π d
References
- Faraday, Maxwell, and the Electromagnetic Field:by Basil Mahon and Nancy Forbes.
- ELECTROMAGNETISM: Theory and Applications Book by ASHUTOSH PRAMANIK
- Field and wave electromagnetics Textbook by David K. Cheng
Unit 4
Static Magnetic Fields
Let us consider a conductor carrying direct current I and a steady magnetic field is produced around it. The law helps us to obtain magnetic field intensity 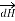 produced at a point P due to differential current element idL. The current carrying conductor is as shown in the figure.
produced at a point P due to differential current element idL. The current carrying conductor is as shown in the figure.
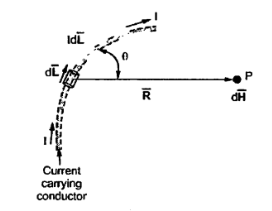
Consider differential length dL and differential current IdL. This is a small part of the current carrying conductor. The point P is at a distance R from differential current element.  is the angle between the differential current element and the line joining point P to the differential current element?
is the angle between the differential current element and the line joining point P to the differential current element?
Bio-Savart Law states that the magnetic field intensity  produced at point P due to differential current IdL is,
produced at point P due to differential current IdL is,
Proportional to the product of current I and differential length dL.
The sine of angle between the element and the line joining point P to the element.
Inversely proportional to the square of distance R between point P and the element.
Bio-Savart law can be stated as ,
d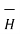 α I dL sin Ɵ / R 2
α I dL sin Ɵ / R 2
d =k I dL sin Ɵ / R 2
=k I dL sin Ɵ / R 2
Where k = constant of proportionality
In SI units, k = 1/ 4 π.
d = I dL sin Ɵ / 4πR 2
= I dL sin Ɵ / 4πR 2
In vector form,
Let dL = Magnitude of vector length 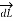 and
and
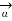 R = Unit vector in the direction from differential current element to point P.
R = Unit vector in the direction from differential current element to point P.
Then from rule of cross product ,
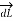 x
x 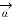 R = dL |
R = dL | R| sin Ɵ = dL sin Ɵ |
R| sin Ɵ = dL sin Ɵ | R|=1
R|=1
Replacing we get
d = I d
= I d  x
x 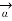 R / 4πR 2 A/m
R / 4πR 2 A/m
 R =
R =  / |
/ | =
= 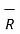 / R
/ R
d = I d
= I d 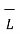 x
x 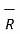 / 4πR 3 A/m
/ 4πR 3 A/m
This is the mathematical form of Bio-Savarts Law.
According to direction of cross product the direction of  is normal to the plane containing two vectors and the normal direction along the progress of right- handed screw turned from
is normal to the plane containing two vectors and the normal direction along the progress of right- handed screw turned from 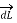 through smaller angle
through smaller angle 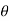 towards the line joining element to point P.
towards the line joining element to point P.
Therefore, direction of 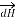 is normal to the plane of paper.
is normal to the plane of paper.
According to right- handed screw rule the direction of 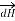 is going into the plane of paper.
is going into the plane of paper.
The entire conductor is made of differential elements . Therefore , in order to obtain the total magnetic field take the integral
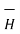 =
= 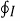 d
d 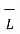 x
x  R / 4πR 2
R / 4πR 2
The closed line integral is required to ensure that all the current elements are considered because current can flow only in the closed path provided by close circuit.
If the current element is considered at point 1 and point P at point 2 as shown in the figure, then
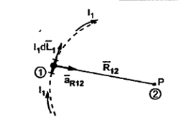
D  2 = I1 d
2 = I1 d  1 x x
1 x x 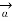 R 12 / 4πR 2 12
R 12 / 4πR 2 12
Where
I1 = current flowing through dL1 at point 1.
DL1 = Differential vector length at point 1
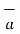 R12 = Unit vector in the direction from element at point 1 to point P at point2.
R12 = Unit vector in the direction from element at point 1 to point P at point2.
 R12 =
R12 =  / |
/ |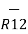 | =
| = 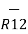 / R12
/ R12
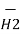 =
=  d
d  x
x 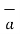 R12 / 4 π R 2 12 A/m
R12 / 4 π R 2 12 A/m
This integral form is called Biot-Savart law.
Problem:
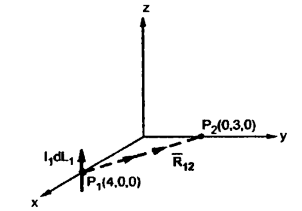
Find the incremental field strength at P2 due to the current element of 2πa2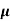 Am at P1. The co-ordinates of P1 and P2 are (4,0,0) and (0,3,0) respectively.
Am at P1. The co-ordinates of P1 and P2 are (4,0,0) and (0,3,0) respectively.
Solution:
The two points P1 and P2 along with the I1dL1 current element at I1 are shown in figure.
According to Bio-Savart law
d  = I1 d
= I1 d  x
x 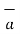 R12 / 4 π R 2 12
R12 / 4 π R 2 12
 = (0-4)
= (0-4) 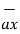 + (3-0) ay + 0. Az
+ (3-0) ay + 0. Az
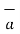 R12 =
R12 =  12 /|
12 /| 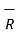 12 |
12 |
= -4 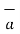 x + 3
x + 3  y /
y / 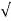 16 + 9
16 + 9
= -4 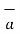 x + 3
x + 3 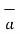 y /5
y /5
While I1 dL1 = 2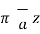
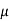 A m.
A m.
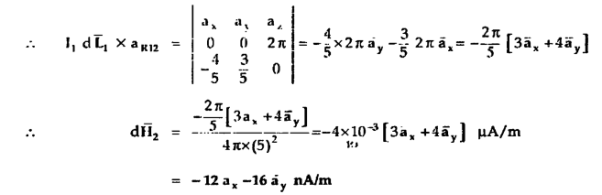
3.3 Ampere ‘s Circuit Law –
Gauss’s Law is useful to obtain 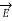 in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
It states that
The line integral of magnetic field intensity  around closed path is exactly equal to direct current enclosed by that path.
around closed path is exactly equal to direct current enclosed by that path.
The mathematical representation of Ampere’s circuital law is
 ---------------------(1)
---------------------(1)
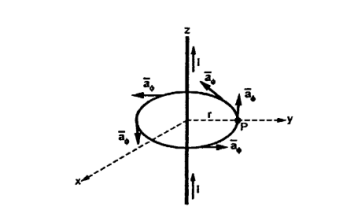
This law is useful to determine 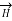 when current distribution is symmetrical.
when current distribution is symmetrical.
Proof:
Consider a long straight conductor carrying direct current I placed along z axis as shown in figure. Consider a closed circular path of radius r which encloses the straight conductor carrying direct current I. The point P is at perpendicular distance r from the conductor.
Consider  at point P which is direction
at point P which is direction 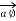 direction tangential to circular path at point P.
direction tangential to circular path at point P.
Therefore,

While  obtained at point P, from Biot-Savart law due to infinitely long conductor is,
obtained at point P, from Biot-Savart law due to infinitely long conductor is,
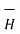 = 1/ 2 π r .
= 1/ 2 π r .  ɸ . r dɸ .
ɸ . r dɸ . 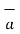 ɸ
ɸ
= 1/ 2 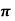 r . dɸ = 1/ 2 π . dɸ
r . dɸ = 1/ 2 π . dɸ
Integrating 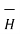 .
. 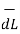 over the entire closed path
over the entire closed path
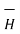 .
. 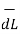 =
=  dɸ = 1/ 2 π [ɸ] 0 2π = I. 2 π/ 2 π
dɸ = 1/ 2 π [ɸ] 0 2π = I. 2 π/ 2 π
This proves that the integral 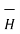 .
. 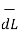 along closed path gives the direct current enclosed by that closed path.
along closed path gives the direct current enclosed by that closed path.
Steps to Apply Amper’s Circuital Law:
Step1: Consider a closed path preferably symmetrical such that it encloses the direct current I once. This is Amperian path.
Step2: Consider differential length 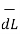 depending upon the co-ordinate system used.
depending upon the co-ordinate system used.
Step3: Identify the symmetry and find in which direction 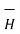 exists according to co-ordinate system used.
exists according to co-ordinate system used.
Step 4: Find 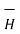 .
.  . Make sure that
. Make sure that 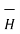 and
and 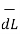 are in the same direction.
are in the same direction.
Step 5: Find the integral of  .
. 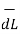 around the closed path. And equate it to current I enclosed by the path.
around the closed path. And equate it to current I enclosed by the path.
To apply Ampere’s circuital law the following conditions must be satisfied,
- The
 ie either tangential or normal to the path, at each point of the closed path.
ie either tangential or normal to the path, at each point of the closed path. - The magnitude of
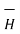 must be same at all points of the path where
must be same at all points of the path where  is tangential.
is tangential.
 due to straight conductors.
due to straight conductors.
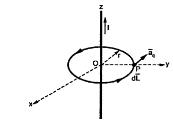
Consider an infinitely long straight conductor which is placed along z-axis carrying direct current I as shown in figure. Consider the Amperian closed path enclosing the conductor as shown in figure. Consider point P on the closed path at which  is obtained. The radius of the path is r from the conductor. The magnitude of
is obtained. The radius of the path is r from the conductor. The magnitude of 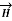 depends on r and the direction is always tangential to the closed path. So,
depends on r and the direction is always tangential to the closed path. So, 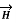 has only component in
has only component in 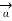
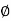 direction say H
direction say H  .
.
Consider elementary length 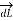 at point P in cylindrical co-ordinates it is r d
at point P in cylindrical co-ordinates it is r d in
in 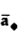 .
.
 = Hɸ
= Hɸ  ɸ and
ɸ and  = r dɸ .
= r dɸ .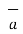 ɸ
ɸ
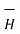 .
. 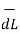 = Hɸ
= Hɸ  ɸ . r dɸ .
ɸ . r dɸ .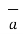 ɸ = Hɸ r dɸ
ɸ = Hɸ r dɸ
According to Ampere’s circuit law ,
 = I
= I
 ɸ . r. dɸ = I
ɸ . r. dɸ = I
Hɸ . r  . dɸ = I
. dɸ = I
Hɸ . r [2π] =I
Hɸ = 1/ 2π r
Hence 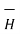 at point P is given by
at point P is given by
 = Hɸ.
= Hɸ.  ɸ = 1/ 2 π r .
ɸ = 1/ 2 π r . 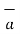 ɸ
ɸ
The total magnetic lines of force that is magnetic flux crossing a unit area in a plane at right angles to the direction of flux is called magnetic flux density. It is denoted 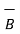 and is vector quantity. It is measured in weber per square metre called as Tesla.
and is vector quantity. It is measured in weber per square metre called as Tesla.
If Vm is the scalar magnetic potential, then it must satisfy the equation
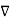 x
x 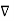 Vm =0
Vm =0
But the scalar magnetic potential is related to the magnetic field intensity 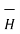 as
as
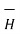 = -
= - 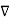 Vm
Vm
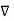 x (-
x (- 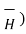 =0 that is
=0 that is 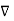 x (
x ( 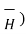 =0
=0
 x (
x ( 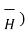 =
= 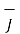 that is
that is 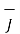 =0
=0
Thus scalar magnetic potential Vm can be defined for source free region where  that is the current density is zero.
that is the current density is zero.
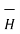 = -
= -  Vm only for
Vm only for  =0
=0
Vector magnetic potential:
The vector magnetic potential is denoted as 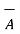 and measured in Wb/m . It has to satisfy equation that divergence of a curl of a vector is always zero.
and measured in Wb/m . It has to satisfy equation that divergence of a curl of a vector is always zero.
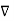 .
. 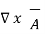 =0
=0
 .
. 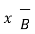 =0
=0
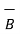 =
= 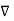

The curl of a vector magnetic potential is the flux density.
Now  .
. 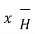 =
= 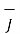
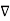
 /
/ 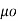 =
= 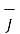
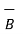 =
= 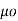
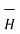
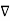
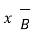 =
= 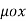
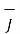
 x
x 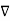 x A = =
x A = = 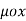

Using vector identity to express on L.H.S we write
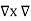
 = =
= = 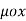 J
J
J = 1/ 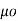 [
[ 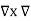
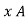 ] = 1/ 1/
] = 1/ 1/ 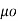 [
[ 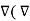 x
x  ) -
) - 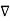 2
2 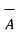 ]
]
Thus if vector magnetic potential is known then current density J can be obtained.
Consider two current carrying conductors placed parallel to each other. Each of these conductors produce its own flux around it. So when such two conductors are placed close to each other there exists a force due to the interaction of two fluxes. The force between such parallel current carrying conductors depends on the directions of the two currents.
If the directions of both the currents are same then the conductors experience a force of attraction. If the direction of two currents are opposite to each other then the conductors experience force of repulsion.
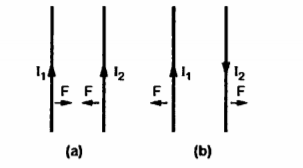
Let us consider two current elements I1  and I2
and I2 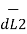 as shown in the figure. As the currents are flowing in the same direction through the elements the force d(
as shown in the figure. As the currents are flowing in the same direction through the elements the force d(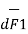 1) exerted on element I1
1) exerted on element I1 due to magnetic field
due to magnetic field  produced by other element I2
produced by other element I2 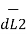 is the force of attraction.
is the force of attraction.
From the equation of force the force exerted on a differential current element is given by
d(d  ) = I1
) = I1 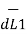 x d
x d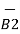
According to Bio-Savart’s law the magnetic field produced by the current element I2  is given by free space
is given by free space
x d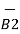 =
= 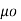 d
d 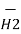 =
=  [ I2
[ I2  x
x  R21 / 4
R21 / 4 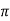 R 2 21
R 2 21
Substituting the value of d
d ( d 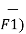 =
=  x I1
x I1 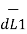 x ( I2
x ( I2 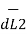 x
x 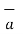 R21 ) / 4
R21 ) / 4 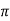 R 2 21
R 2 21
The equation represents force between two current elements.
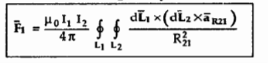
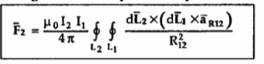
The above equation indicates that the forces F1 and F2 obey Newton’s third law that for every action there is equal and opposite reaction.
For the two current carrying conductors of length l each the force exerted is given by
F = 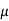 I1 I2 l / 2 π d
I1 I2 l / 2 π d
References
- Faraday, Maxwell, and the Electromagnetic Field:by Basil Mahon and Nancy Forbes.
- ELECTROMAGNETISM: Theory and Applications Book by ASHUTOSH PRAMANIK
- Field and wave electromagnetics Textbook by David K. Cheng
Unit 4
Static Magnetic Fields
Let us consider a conductor carrying direct current I and a steady magnetic field is produced around it. The law helps us to obtain magnetic field intensity 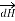 produced at a point P due to differential current element idL. The current carrying conductor is as shown in the figure.
produced at a point P due to differential current element idL. The current carrying conductor is as shown in the figure.
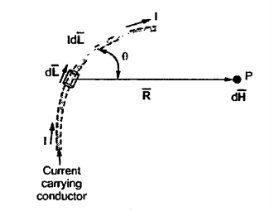
Consider differential length dL and differential current IdL. This is a small part of the current carrying conductor. The point P is at a distance R from differential current element. 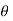 is the angle between the differential current element and the line joining point P to the differential current element?
is the angle between the differential current element and the line joining point P to the differential current element?
Bio-Savart Law states that the magnetic field intensity 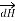 produced at point P due to differential current IdL is,
produced at point P due to differential current IdL is,
Proportional to the product of current I and differential length dL.
The sine of angle between the element and the line joining point P to the element.
Inversely proportional to the square of distance R between point P and the element.
Bio-Savart law can be stated as ,
d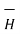 α I dL sin Ɵ / R 2
α I dL sin Ɵ / R 2
d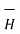 =k I dL sin Ɵ / R 2
=k I dL sin Ɵ / R 2
Where k = constant of proportionality
In SI units, k = 1/ 4 π.
d = I dL sin Ɵ / 4πR 2
= I dL sin Ɵ / 4πR 2
In vector form,
Let dL = Magnitude of vector length 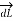 and
and
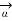 R = Unit vector in the direction from differential current element to point P.
R = Unit vector in the direction from differential current element to point P.
Then from rule of cross product ,
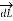 x
x  R = dL |
R = dL |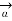 R| sin Ɵ = dL sin Ɵ |
R| sin Ɵ = dL sin Ɵ | R|=1
R|=1
Replacing we get
d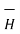 = I d
= I d 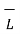 x
x 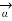 R / 4πR 2 A/m
R / 4πR 2 A/m
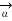 R =
R = 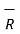 / |
/ |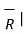 =
= 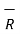 / R
/ R
d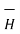 = I d
= I d 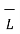 x
x 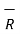 / 4πR 3 A/m
/ 4πR 3 A/m
This is the mathematical form of Bio-Savarts Law.
According to direction of cross product the direction of  is normal to the plane containing two vectors and the normal direction along the progress of right- handed screw turned from
is normal to the plane containing two vectors and the normal direction along the progress of right- handed screw turned from 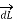 through smaller angle
through smaller angle 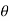 towards the line joining element to point P.
towards the line joining element to point P.
Therefore, direction of 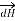 is normal to the plane of paper.
is normal to the plane of paper.
According to right- handed screw rule the direction of 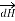 is going into the plane of paper.
is going into the plane of paper.
The entire conductor is made of differential elements . Therefore , in order to obtain the total magnetic field take the integral
 =
=  d
d 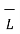 x
x 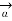 R / 4πR 2
R / 4πR 2
The closed line integral is required to ensure that all the current elements are considered because current can flow only in the closed path provided by close circuit.
If the current element is considered at point 1 and point P at point 2 as shown in the figure, then
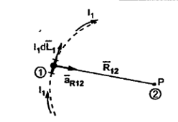
D 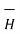 2 = I1 d
2 = I1 d  1 x x
1 x x  R 12 / 4πR 2 12
R 12 / 4πR 2 12
Where
I1 = current flowing through dL1 at point 1.
DL1 = Differential vector length at point 1
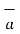 R12 = Unit vector in the direction from element at point 1 to point P at point2.
R12 = Unit vector in the direction from element at point 1 to point P at point2.
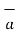 R12 =
R12 = 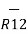 / |
/ |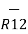 | =
| = 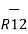 / R12
/ R12
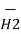 =
=  d
d 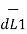 x
x  R12 / 4 π R 2 12 A/m
R12 / 4 π R 2 12 A/m
This integral form is called Biot-Savart law.
Problem:
Find the incremental field strength at P2 due to the current element of 2πa2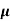 Am at P1. The co-ordinates of P1 and P2 are (4,0,0) and (0,3,0) respectively.
Am at P1. The co-ordinates of P1 and P2 are (4,0,0) and (0,3,0) respectively.
Solution:
The two points P1 and P2 along with the I1dL1 current element at I1 are shown in figure.
According to Bio-Savart law
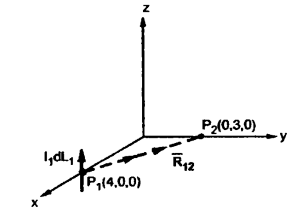
d  = I1 d
= I1 d 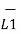 x
x  R12 / 4 π R 2 12
R12 / 4 π R 2 12
 = (0-4)
= (0-4) 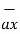 + (3-0) ay + 0. Az
+ (3-0) ay + 0. Az
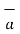 R12 =
R12 = 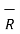 12 /|
12 /|  12 |
12 |
= -4  x + 3
x + 3 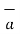 y /
y / 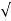 16 + 9
16 + 9
= -4 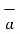 x + 3
x + 3 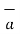 y /5
y /5
While I1 dL1 = 2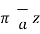
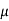 A m.
A m.
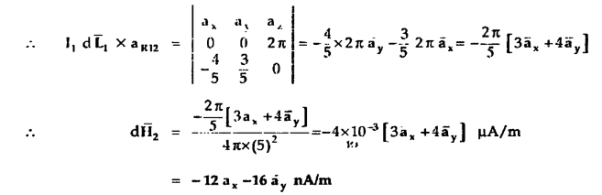
3.3 Ampere ‘s Circuit Law –
Gauss’s Law is useful to obtain  in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
in case of complex problems. I magnetostatics complex problems can be solved using Ampere’s Law.
It states that
The line integral of magnetic field intensity  around closed path is exactly equal to direct current enclosed by that path.
around closed path is exactly equal to direct current enclosed by that path.
The mathematical representation of Ampere’s circuital law is
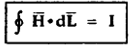 ---------------------(1)
---------------------(1)
This law is useful to determine  when current distribution is symmetrical.
when current distribution is symmetrical.
Proof:
Consider a long straight conductor carrying direct current I placed along z axis as shown in figure. Consider a closed circular path of radius r which encloses the straight conductor carrying direct current I. The point P is at perpendicular distance r from the conductor.
Consider 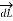 at point P which is direction
at point P which is direction 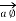 direction tangential to circular path at point P.
direction tangential to circular path at point P.
Therefore,

While 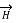 obtained at point P, from Biot-Savart law due to infinitely long conductor is,
obtained at point P, from Biot-Savart law due to infinitely long conductor is,
 = 1/ 2 π r .
= 1/ 2 π r .  ɸ . r dɸ .
ɸ . r dɸ . 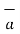 ɸ
ɸ
= 1/ 2 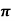 r . dɸ = 1/ 2 π . dɸ
r . dɸ = 1/ 2 π . dɸ
Integrating 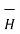 .
.  over the entire closed path
over the entire closed path
 .
. 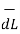 =
= 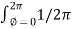 dɸ = 1/ 2 π [ɸ] 0 2π = I. 2 π/ 2 π
dɸ = 1/ 2 π [ɸ] 0 2π = I. 2 π/ 2 π
This proves that the integral 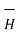 .
. 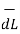 along closed path gives the direct current enclosed by that closed path.
along closed path gives the direct current enclosed by that closed path.
Steps to Apply Amper’s Circuital Law:
Step1: Consider a closed path preferably symmetrical such that it encloses the direct current I once. This is Amperian path.
Step2: Consider differential length 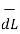 depending upon the co-ordinate system used.
depending upon the co-ordinate system used.
Step3: Identify the symmetry and find in which direction 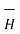 exists according to co-ordinate system used.
exists according to co-ordinate system used.
Step 4: Find 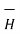 .
.  . Make sure that
. Make sure that 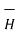 and
and  are in the same direction.
are in the same direction.
Step 5: Find the integral of 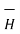 .
.  around the closed path. And equate it to current I enclosed by the path.
around the closed path. And equate it to current I enclosed by the path.
To apply Ampere’s circuital law the following conditions must be satisfied,
- The
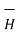 ie either tangential or normal to the path, at each point of the closed path.
ie either tangential or normal to the path, at each point of the closed path. - The magnitude of
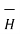 must be same at all points of the path where
must be same at all points of the path where 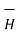 is tangential.
is tangential.
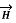 due to straight conductors.
due to straight conductors.
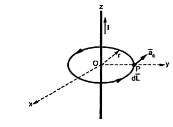
Consider an infinitely long straight conductor which is placed along z-axis carrying direct current I as shown in figure. Consider the Amperian closed path enclosing the conductor as shown in figure. Consider point P on the closed path at which 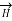 is obtained. The radius of the path is r from the conductor. The magnitude of
is obtained. The radius of the path is r from the conductor. The magnitude of 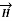 depends on r and the direction is always tangential to the closed path. So,
depends on r and the direction is always tangential to the closed path. So, 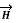 has only component in
has only component in 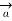
 direction say H
direction say H  .
.
Consider elementary length  at point P in cylindrical co-ordinates it is r d
at point P in cylindrical co-ordinates it is r d in
in 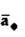 .
.
 = Hɸ
= Hɸ  ɸ and
ɸ and 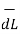 = r dɸ .
= r dɸ .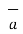 ɸ
ɸ
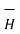 .
.  = Hɸ
= Hɸ  ɸ . r dɸ .
ɸ . r dɸ .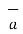 ɸ = Hɸ r dɸ
ɸ = Hɸ r dɸ
According to Ampere’s circuit law ,
 = I
= I
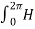 ɸ . r. dɸ = I
ɸ . r. dɸ = I
Hɸ . r 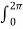 . dɸ = I
. dɸ = I
Hɸ . r [2π] =I
Hɸ = 1/ 2π r
Hence 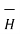 at point P is given by
at point P is given by
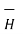 = Hɸ.
= Hɸ. 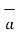 ɸ = 1/ 2 π r .
ɸ = 1/ 2 π r . 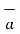 ɸ
ɸ
The total magnetic lines of force that is magnetic flux crossing a unit area in a plane at right angles to the direction of flux is called magnetic flux density. It is denoted 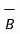 and is vector quantity. It is measured in weber per square metre called as Tesla.
and is vector quantity. It is measured in weber per square metre called as Tesla.
If Vm is the scalar magnetic potential, then it must satisfy the equation
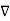 x
x 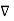 Vm =0
Vm =0
But the scalar magnetic potential is related to the magnetic field intensity 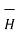 as
as
 = -
= - 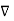 Vm
Vm
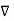 x (-
x (-  =0 that is
=0 that is  x (
x ( 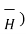 =0
=0
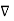 x (
x ( 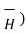 =
= 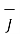 that is
that is 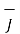 =0
=0
Thus scalar magnetic potential Vm can be defined for source free region where  that is the current density is zero.
that is the current density is zero.
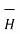 = -
= - 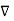 Vm only for
Vm only for 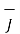 =0
=0
Vector magnetic potential:
The vector magnetic potential is denoted as 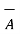 and measured in Wb/m . It has to satisfy equation that divergence of a curl of a vector is always zero.
and measured in Wb/m . It has to satisfy equation that divergence of a curl of a vector is always zero.
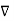 .
. 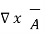 =0
=0
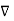 .
.  =0
=0
 =
= 
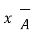
The curl of a vector magnetic potential is the flux density.
Now  .
.  =
= 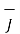
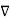
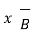 /
/ 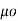 =
= 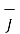
 =
= 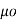


 =
= 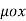
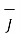
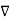 x
x 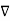 x A = =
x A = = 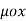
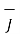
Using vector identity to express on L.H.S we write

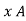 = =
= = 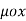 J
J
J = 1/  [
[ 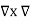
 ] = 1/ 1/
] = 1/ 1/ 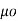 [
[ 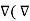 x
x 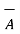 ) -
) - 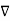 2
2 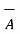 ]
]
Thus if vector magnetic potential is known then current density J can be obtained.
Consider two current carrying conductors placed parallel to each other. Each of these conductors produce its own flux around it. So when such two conductors are placed close to each other there exists a force due to the interaction of two fluxes. The force between such parallel current carrying conductors depends on the directions of the two currents.
If the directions of both the currents are same then the conductors experience a force of attraction. If the direction of two currents are opposite to each other then the conductors experience force of repulsion.
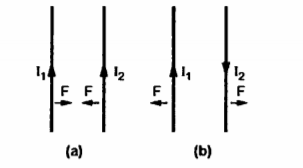
Let us consider two current elements I1 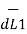 and I2
and I2 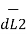 as shown in the figure. As the currents are flowing in the same direction through the elements the force d(
as shown in the figure. As the currents are flowing in the same direction through the elements the force d(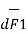 1) exerted on element I1
1) exerted on element I1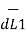 due to magnetic field
due to magnetic field 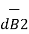 produced by other element I2
produced by other element I2  is the force of attraction.
is the force of attraction.
From the equation of force the force exerted on a differential current element is given by
d(d  ) = I1
) = I1 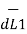 x d
x d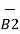
According to Bio-Savart’s law the magnetic field produced by the current element I2  is given by free space
is given by free space
x d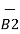 =
= 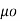 d
d 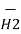 =
= 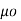 [ I2
[ I2  x
x 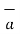 R21 / 4
R21 / 4 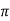 R 2 21
R 2 21
Substituting the value of d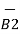
d ( d 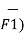 =
= 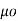 x I1
x I1  x ( I2
x ( I2 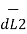 x
x 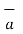 R21 ) / 4
R21 ) / 4  R 2 21
R 2 21
The equation represents force between two current elements.
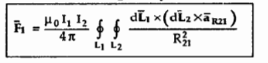
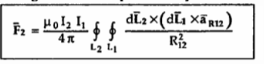
The above equation indicates that the forces F1 and F2 obey Newton’s third law that for every action there is equal and opposite reaction.
For the two current carrying conductors of length l each the force exerted is given by
F = 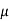 I1 I2 l / 2 π d
I1 I2 l / 2 π d
References
- Faraday, Maxwell, and the Electromagnetic Field:by Basil Mahon and Nancy Forbes.
- ELECTROMAGNETISM: Theory and Applications Book by ASHUTOSH PRAMANIK
- Field and wave electromagnetics Textbook by David K. Cheng