UNIT 3

Discrete time systems

3.1 Transform and its applications to the analysis of LTI Systems

1. Z transform for Discrete System

Definition:

The Z transform for discrete time system x(n ) is defined as

X(z) = 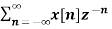   ------- (1) where z is a complex variable.

In polar form z can be expressed as

z  = r e jw  ---------------(2) where r is the radius of a circle.

For n≥ 0

X(z ) = 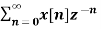       --------- (3)which is called one-sided z-transform.

By substituting z = r e jw

X(r e jw)  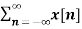=    (r e jw) –n     ------- (4)

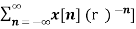    e- jwn       ----- (5)

Equation(5) represents the Fourier transform of the signal x(n) r-n

Hence the inverse DTFT  X(r ejw) must be x(n) r-n.

x(n) r-n = 1/2π 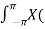r e jw )  e jwn dw

On multiplying both sides by rn  we get

x(n) = 1/ 2 π 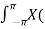  r ejw) (r ejw ) n dw                  [ z = r ejw

Let z= r e jw  and dw= dz/jz 

Dz = r ejw dw

Dw = dz/jre jw

Example

Find the z-transform for the sequence

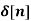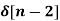x[n] = 2 + 3 + 5 + 2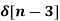

Solution:

X(z) = 2 + 3 z-1 + 5 z -2 + 2 z -3   

Example

If X(z)= 4 – 5 z-2 + z-3 – 2z -4    then find x[n]

Solution:

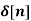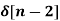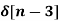x[n] = 4 - 5 + - 2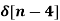

Example : Find the z-transform and ROC of the signal

x(n) = an u(n)

Solution: 

X(z) =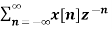 

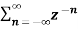= an u(n) -----(1)    u(n) = 0 for n<0

1 for n≥0

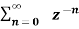= an ------- (2)

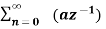= n   ------- (3)

This is a geometric series of infinite length that is

a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1

Then from equation (3) it converges when |az-1| < 1 or |z| >|a|

Therefore

X(z) = 1/ 1-az-1:  ROC    |z| > |a|

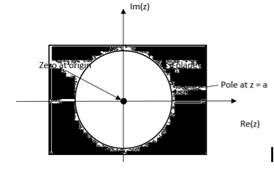
Find the z-transform of the signal x(n) =-b n u(-n-1). Find ROC

X(z) =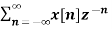 

X(z) = 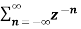 bn u(-n-1)                                                                   u(-n-1) =0 for n ≥0

= 1 for n ≤ -1

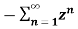= bn   = b-1  =

= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1                                                               |z| < |b|

Find the z-transform of x(n) = an u(n) – bn u(-n-1)

X(z) =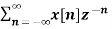 

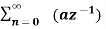=  n  + b-1

= z/z-a + z/z-b       ROC |a| < |z| < |b|

|b|< |a|

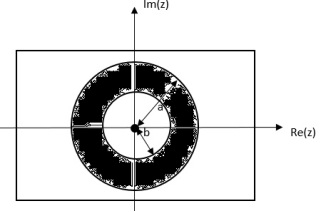
|b| >|a|

Find the z-transform of x(n) = {1,2,3,2}

Given x(0) = 1  x(1) =2   x(2) =3    x(3) = 2

X(z) =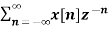 

X(z) = 1+ 2z-1 + 3 z-2 +2 z-3 

Properties of Convergence

1. The ROC is a ring or disk in the z-plane centered at the origin.
2. ROC cannot contain any poles.
3. If x(n) is finite duration casual sequence then the ROC is the entire z-plane except at z=0.
4. If x(n) is finite duration anti-casual sequence then ROC is the entire z-plane except at z=∞
5. If x(n) is a finite duration two-sided sequence ROC is the entire z-plane except at z=0 and z=∞
6. If x(n) is a finite duration two-sided sequence then ROC will consist of a ring in the z-plane bounded on the interior and exterior by a pole not containing any poles.
7. The ROC of an LTI system contains unit circle.
8. ROC must be a connected region.

Find the z-transform of the signal x(n) = sin w0n u(n) and find ROC.

X(z) =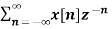 

X(z) =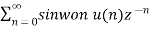 

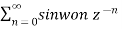=       sin = ej - e-j / 2j

= 1/2j 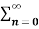       (ejw0n – e –jwon )z-n 

= 1/2j 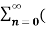ejwon z-1) n - 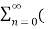e-jw0z-1) n

1/2j[ 1/1-ejw0z-1 – 1/1-e-jw0z-1]

= sin w0 z-1/ 1-2cos(wo)z-1 + z-2       ROC |z| >1

2. LTI system

Properties of z-transform

• Linearity

If X1(z) = Z{x1(n)} and X2(z) = Z{x2(n)}

Then

Z{ax1(n) + bx2(n)} = a X1(z) + b X2(z)

Proof:

Z{ax1(n) + b x2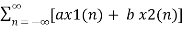(n) }=   z-n

= a 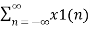   z-n + b   z-n 

= a X1(z) + b X2(z)

• Time Shifting

If X(z) = Z{x(n)} and initial conditions for x(n) are zero then

Z{x(n-m) } = z-m X(z)

Where m is a positive integer.

Proof:

Z {x(n-m)} = 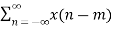  z-n

Let n-m = p then n= p+m

Z{x(n-m)} = 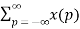  z –(m+p)

z-m 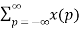z-p  = z-m X(z)

• Multiplication by exponential sequence

If X(z ) = Z{x(n)} then

Z [ an x(n) ] = X(a-1 z)

Proof:

Z{ an x(n) } = 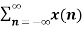 an z-n

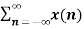=   (az-1)n 

= X(az-1)

• Convolution

We know that

Z{x(n) * h(n) } = X(z) H(z)

Proof:

Let y(n) = x(n) * h(n)

y(n)=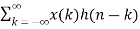

Taking z-transform on both sides we obtain

Y(z) =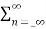 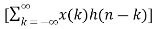z-n

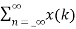z-k 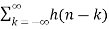   z –(n-k)       Replacing n-k by l

  z-k    z-l

= X(k) Z(k)

• Time Reversal

If X(z) = Z{x(n)} then

Z{x(-n)} = X(z-1}

Proof:

Z{x(-n)} = 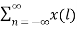( z-l) -1           l=-n

= X(z-1)

• Multiplication by n

If Z{x(n)} = X(z) then

Z{n x(n)} = -z d/dz X(z)

X(z) =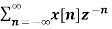 

Z{n x(n)} =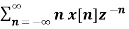

= z 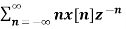-1

= z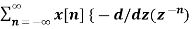

=  -z }

= -z d/dz {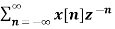

= -z d/dz X(z)

Problems:

Find the z-transform of the sequence

x(n) = a n-1 u(n-1)

We know that x(n) = an u(n)  is

X(z) = 1/1/az-1

By using time shifting property we have Z{ x(n-k)} = z-k X(z)

Therefore

Z{an-1 u(n-1)} = z-1/ 1-az-1  = 1/z-a.            ROC |z| > |a|

• Find the z-transform of the sequence

x(n) = an cos nπ/2

Z{ cos w0n} = 1- (cos w0) z-1/ 1 –(2 cos w0) z-1 + z-2   

Since w0=π/2

Z{ cos π/2 n u(n)} = 1/1 + z-2

Using exponential sequence property

Z{ an x(n) } = X(a-1 z)

Z{ an cos nπ/2} = 1/1+(a-1z)-2 = 1/ 1 + a2/z2  = z2/ a2 + z2  

• Find the z transform of the sequence x(n) = n u(n)

The z-transform of unit step sequence is given by

Z{u(n)} = z/z-1

Z{ n u(n)} = -z d/dz (z/z-1)

= z/(z-1)2    

• If x(n) = x1(n) * x2(n) where x1(n) = (1/3)n u(n) and x2(n) = (1/5)n u(n). Find X(z) by using convolution property.

X1(z) = 1/ 1- (1/3)z-1         X2(z) = 1/1- (1/5) z-1 

X(z) = 1/1-(1/3)z-1 . 1/1-(1/5) z-1  

Using z-transform find the convolution of two sequences.

x1(n) = {1,2,-1,0,3}        x2(n) = { 1,2,-1}

Z{ x1(n) * x2(n)} = X1(z) . X2(z)

X1(z) = 1 + 2z-1 – z-2 + 3 z-4

X2(z) = 1 + 2z-1 – z-2 

(1 + 2z-1 – z-2 + 3 z-4  )  (1 + 2z-1 – z-2  )

= 1 + 4z-1 + 2z-2 – 4 z- 3 + 4 z-4 + 6 z- 5 – 3 z-6 

• Determine the z-transform of the signal

x(n ) = rn (sin w0n ) u(n)

Z{(sin w0n ) u(n)}  = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2

Z{ an x(n)} = X(a-1 z)

Therefore

Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2  

= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2

• Determine the signal x(n) whose z-transform is given by

X(z) = log(1- az-1)

X(z)= log(1-az-1)

Differentiating both sides we get

d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1

-z d/dz { X(z)} = -az-1/1-az-1

= -az-1[ 1/1-az-1]

= -a Z[ a n-1 u(n-1)]                           -------- (1)

From differentiation property

Z{ n x(n)} = -z d/dz [ X(z)]            ------- (2)

Comparing (1) and (2) we get

n  x(n) = -a [ a n-1 u(n-1)]

Or x(n) = -a [a n-1 u(n-1)]/n

• Determine the z-transform of the signal

x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)

=½ n2 (1/3) n-1 u(n-1) +1/2 n (1/3) n-1 u(n-1)

We know that

Z[(1/3) n u(n)] = z/ z-1/3

Using time-shifting property

Z{(1/3) n-1 u(n-1)] = 1/ z- 1/3

Z [ n (1/3) n-1 u(n-1)] = -z d/dz [1/z-(1/3)]

=-z d/dz( 1/z-1/3)= -z [-1/(z-1/3) 2]= z/ (z-1/3)2

Z [ n2 (1/3) u(n-1)] = -z d/dz [ z/(z-1/3)2]

= z(z+1/3)/(z-1/3)2 

= -z [ (z-1/3)2 -2z(z-1/3)/(z-1/3)4

= z(z+1/3)/(z-1/3)3 

X(z) = ½[z(z+1/3)/(z-1/3)3 + z/ (z-1/3)2]

= z2/(z-1/3)3

• Inverse  Z-transform

There are three methods that are often used to find inverse z-transform.

• Long Division Method
• Partial fraction method
• Convolution Method

• Long Division Method

If X(z) is the ratio of two polynomials then

X(z) = N(z)/D(z ) = b0 + b1 z-1 + b2 z-2 +……….. +bM z-M   

1+ a1z-1 + a2 z-2 + …………. + aN z-N 

Using long division method Find the inverse z-transform of the sequence of

X(z) = z+1

z2 +3z + 2

z-1 + 4z-2 + 10 z-3 +22 z-4

z2 -3z +2                                z+1

z- 3 + 2z-1

4 – 2z-1

4 – 12 z-1 + 8 z-2

10z-1 – 8z-2

10 z-1 – 30z-2 +20 z-3

22 z-2 – 20 z-3

22 z-2 -66 z-3 +44 z-4

46 z-3 – 44 z-4

X(z) = z-1 + 4 z-2 + 10 z-3 + 22z-4

x(n) = { 0,1,4,10,22………}

• Partial fraction Method

Find the partial fraction method of

X(z) = ¼ z-1

(1 – ½ z-1)(1-1/4 z-1)

X(z) =         A                +          B

Z (1-1/2z-1)      (1 – ¼ z-1)

By solving A= 1 and B=-1

Therefore,

X(z) =   z     -       z 

z-1/2 z-1/4

x(n) = (1/2) n u(n) – (1/4) n u(n)

Find the partial fraction of

X(z) =           1

1+ z-1 + z-2

X(z) =      z

z2 + z + 1

=   z

(z + 0.5 +j 0.866)(z+0.5 – j0.866)

X(z)    =      c                      +                      c* 

z    z-(-0.5 +j0.866) z – (- 0. 5 – j 0.866)

X(z)    =      0.5+j0.288                      +          0.5 – j 0.288 

z    z-(-0.5 +j0.866)  z – (- 0. 5 – j 0.866)

X(z)  =       0.5+j0.288  z                    +          0.5 – j 0.288  z

z-(-0.5 +j0.866)  z – (- 0. 5 – j 0.866)

By taking inverse z-transform both sides we get

= (0.5+j0.288)( (-0.5 +j0.866) n u(n) +(0.5+j0.288)( (-0.5 -j0.866) n u(n

• Convolution Method

Using convolution method  find

X(z) = 1 + 3z-1

1 + 3z-1 + 2z-2

= z(z+3)

(z+1)(z+2)  

X1(z) =     z       X2(z) = z+3     =  z       + z-1 3z

z+1     z+2     z+2            z+2

x1(n) = (-1) n u(n)

x2(n) = (-2) n u(n) + 3 (-2) n-1 u(n-1)

x(n) = x1(n) * x2(n)

= (-1) n u(n) * [ (-2) n u(n) + 3 (-2) n-1 u(n-1)]

= (-1) n u(n) *  (-2) n  u(n) + 3 (-1) n u(n) * (-2) n-1 u(n-1)

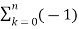= k u(k) (-2) n-k  u(n-k) + 3 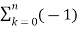k u(k) (-2) n-k-1  u(n-k-1)

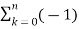= (-2)n k (-2) –k + 3(-2) n-1 k (-2) –k

= (-2) n 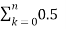    k  + 3 (-2) n-1  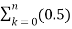 k  

= (-2) n  [ 1-(0.5) n+1 ]   + 3 (-2) n-1 [ 1- (0.5) n]

1 – 0.5   1 – 0.5

x(n)  = [ 2(-1)n – (-2)n]  u(n)

3.  Solution to Difference Equation using z-transform

Z transform converts the difference into algebraic equation in z-domain.

Find the impulse response and step response for the following systems:

y(n) = -  ¾ y(n-1) + 1/8 y(n-2) = x(n)

y(n)  - ¾ y(n-1) + 1/8 y(n-2) = x(n)

Taking z-transform on both sides we get

Y(z) – ¾ [ z-1 Y(z) + y(-1) ] +1/8 [ z-2 Y(z) + z-1 y(-1)+y(-2)] = X(z)

Substituting y(-1)=y(-2)= 0

Y(z) -3/4 z-1 Y(z) + 1/8 z-2 Y(z) = X(z)

Y(z) =     1____________

1-     ¾ z-1 + 1/8 z-2

Impulse response

x(n) = 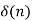       X(z) =1

Y(z) =    1____________           =      1____________ 

1-     ¾ z-1 + 1/8 z-2                 1-  ¾ z-1 + 1/8 z-2  

Y(z)  =  z__________       =        A___        +    B__

X(z) (z-1/2)(z-1/4)  (z-1/2)            (z-1/4)

By solving A=2 and B=-1.

Y(z) = 2 z          -       z

z-1/2       (z-1/4)

y(n) = 2 (1/2)n u(n) – (1/4) n u(n).

Step Response

x(n) = u(n)   X(z) = z/z-1

Y(z)  =         1_______

X(z)   1-3/4 z-1 + 1/8 z-2

Y(z) = z     z2___________

z-1  z2 -3/4 z +1/8

Y(z)   =    z2___________

z     z2 -3/4 z +1/8

Y(z)   =    z2___________

z     (z-1)(z-1/2)(z-3/4)

=               A       +     B   +      C

z-1        z-1/2      z- 1/4

By solving A=8/3   B= -2  C= 1/3

Therefore

Y(z) = 8 . z      -2  z   + 1/3 z

3     z-1      z-1/2 z-1/4

y(n) = 8/3 u(n) – 2(1/2)n u(n) +1/3 (1/4) n u(n)