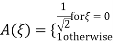UNIT 5
LTI
Fourier series expansion of periodic functional symmetry condition:
Fourier series Representation of Periodic Signals.
To represent any periodic signal x(t) Fourier developed an expression called Fourier series. This is in terms of an infinite sum of sines and cosines or exponentials.
A periodic signal is one which repeats itself periodically over -∞ < t < ∞
A sinusoidal signal x(t) = A sin Ω0t is periodic with period T = 2π/ Ω0.
Let us consider a signal x(t) is a sum of sine and cosine functions whose frequencies are integer multiple of Ω0.
x(t) = a0 + a1 cos (Ω0t) + a2 cos (2 Ω0t) + a3 cos ( 3 Ω0t) ……. + ak cos(k Ω0t) + b1 sin(Ω0t) + b2 sin (2Ω0t) + b3 sin(3Ω0t) + ……….. + bk sin( k Ω0t) ------------- (1)
= a0 + 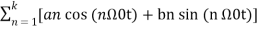
Where a0,a1……. Ak and b1,b2………bk are constants and 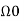 is the fundamental frequency.
is the fundamental frequency.
If the signal x(t) has to be periodic then it should satisfy the condition
x(t + T) = x(t)
x(t + T) = a0 + 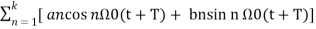 ---------------- (2)
---------------- (2)
= a0 + 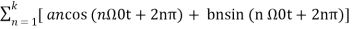 Here
Here 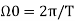
= a0 + 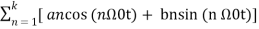 -------------- (3)
-------------- (3)
= x(t)
Evaluation of Fourier Coefficients
The constants a0,a1,a2 ……… an , b1,b2…….bn are called Fourier coefficients. To evaluate ao we have to integrate both sides of eq(3) over one period (t0,t0+T)n of x(t) from an arbitrary time t0.
Thus 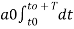 +
+ 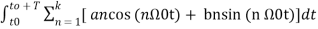 -------(4)
-------(4)
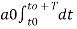 +
+ 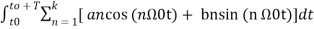 ------(5)
------(5)
= a T + 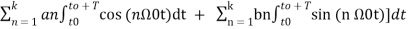 ------(6)
------(6)
Each of the integrals in the summation in the above equation(6) is zero since the net areas of sinusoids over the complete periods are zero for any nonzero integer n .
Therefore
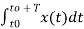 = aoT----------(7)
= aoT----------(7)
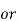 a0 = 1/T
a0 = 1/T 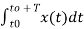 ------(8)
------(8)
To evaluate an and bn
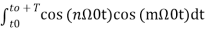 = 0 for m≠n when m=n ≠0 = T/2.-------(9)
= 0 for m≠n when m=n ≠0 = T/2.-------(9)
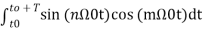 = 0 for values of m and n-------(10)
= 0 for values of m and n-------(10)
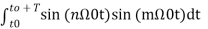 = 0 when m≠n when m=n ≠0 = T/2------(11)
= 0 when m≠n when m=n ≠0 = T/2------(11)
To find an multiply eq(3) by cos( and integrate over one period. That is
and integrate over one period. That is
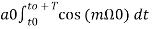 +
+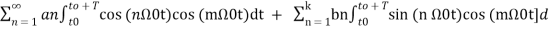 t -----------(12)
t -----------(12)
The first integral on the RHS of the above equation yields to zero because we are integrating over one period.
Therefore
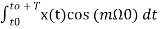 = am T/2-----(13)
= am T/2-----(13)
Am = 2/T 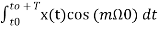 or
or
An = 2/T 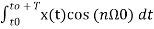
Similarly
Bn=2/T 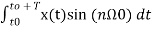
The Fourier series of functions is used to find the steady-state response of a circuit.
Condition for symmetry
There are different types of symmetry that can be used to simplify the process of evaluating the Fourier coefficients.
- Even function symmetry
A function is defined to be even if and only if
f(t) = f(-t)
If a function satisfies the equation then it is said to be even because polynomial functions with only even exponents have this type of behavior.
Av = 2/T 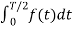
Ak = 4/T 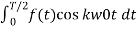 bk=0 for all values of k.
bk=0 for all values of k.
The function is even if the coefficients of b are zero.
When t0 = -T/2 then
Av = 1/T 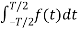
Av = 1/T 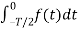 +
+ 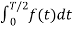
When t= -x we observe that f(-x) =f(x) since it is even function.
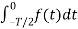 =
= 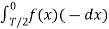 =
= 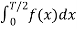
Which does show that integrating from -T/2 to 0 is the same as integrating from 0 to T/2
Therefore
Ak = 2/T 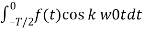 + 2/T
+ 2/T 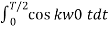
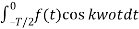 =
= 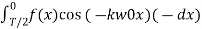 =-
=- 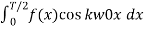
Similarly
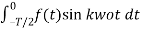 =
= 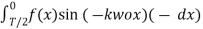 =
= 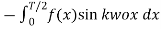
To find the Fourier coefficients the integration lies between 0 and T/2.
- Odd function symmetry
A periodic function is defined to be odd if f( t) = -f(t) due to the fact that polynomial functions with only odd exponents behave this way.
The expression is
Av= 0 ; ak = 0 for all k;
Bk = 4/T 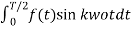
The evenness (oddness) of a function can be dismantled by shifting the periodic function along the time axis.
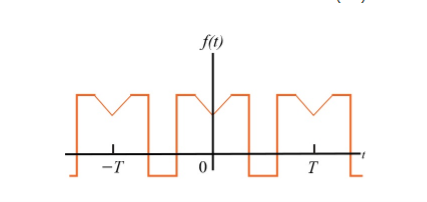
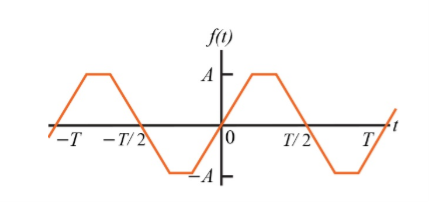
Example :
For the following diagram explain whether it is even or odd.
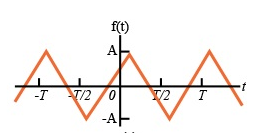
Solution:
The signal is neither even nor odd.
To make the signal even there is a slight shift to be applied as shown in the figure.
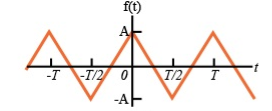
To make the signal odd
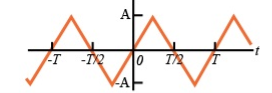
- Half-wave symmetry:
A periodic signal satisfying the condition
x(t) = -x(t ± T/2)
Is said to half symmetry . The Fourier series expansions of such type of periodic signals contains odd harmonics only.
Example:
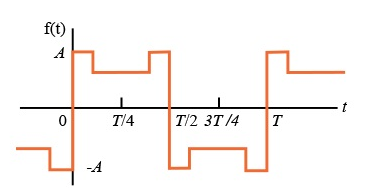
Show that the signal x(t) that satisfies half wave symmetry contains Fourier coefficients with odd harmonics only.
A signal with half-wave symmetry that satisfies the condition x(t+T/2) = - x(t)
The Fourier coefficients of the signal are
Cn = 1/T 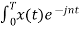 Ω0 dt
Ω0 dt
= 1/T [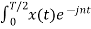 Ω0 dt +
Ω0 dt + 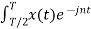 Ω0 dt
Ω0 dt
= 1/T 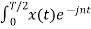 Ω0 dt +
Ω0 dt + 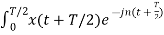 Ω0 dt
Ω0 dt
= 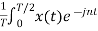 Ω0 dt -
Ω0 dt - 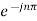
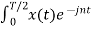 Ω0 dt Here e-jnπ = 1 for n
Ω0 dt Here e-jnπ = 1 for n
Even.
Hence Cn=0
Ω0 = 2π/T
- Quarter-wave symmetry
If a function has half-wave symmetry and symmetry about the midpoint of the positive and negative half-cycles, the periodic function is said to have quarter--wave symmetry.
Problems:
Find the trigonometric Fourier series for the periodic signal x(t) as shown in the figure.
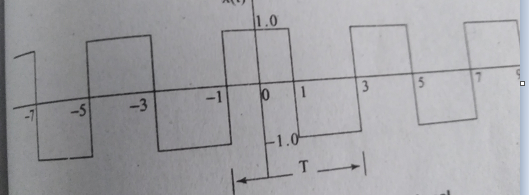
For the given signal the period T =4.
For our convenience let us choose one period signal from t= -1 to t=3
That is t0=-1 and t0+ T =3.
The fundamental frequency
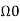 = 2 π/T =2 π/4= π/2.
= 2 π/T =2 π/4= π/2.
x(t) = { 1 for -1 ≤t ≤1
-1 for 1≤t≤3}
a0= 1/T 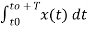
= ¼  = ¼[
= ¼[ 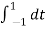 +
+ 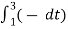 ]
]
= ¼ [ t |-1 1 + (-t)| 1 3 ]
= ¼ [ 1 – (-1) – (3-1)] = 0
a0 = 0.
An = 2/T 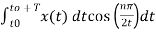
½ 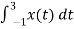
= ½ 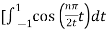 +
+ 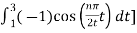
= ½ [ 2/ nπ sin(nπ/2t) | -1 1 - 2/nπ sin(nπ/2t)|1 3
= ½ [ 8/nπ sin(nπ/2)] = 4/nπ sin(nπ/2)
An=4/nπ sin(nπ/2)
Bn = 1/2 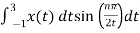
= ½ 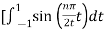 +
+ 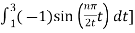
= ½ [ -2 /nπ cos(nπ/2t) | -1 1 + 2/nπ cos(nπ/2t) | 1 3
= -2/nπ(cosnπ/2 – cos nπ/2) + 2/nπ (cos 3nπ/2 – cosnπ/2)
= 0
Therefore 4/nπ sinnπ/2 = { 0 n even
4/nπ = 1,,9,13…..
- 4/nπ 3,7,11,15…….
x(t) = 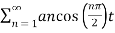
= 4/π cos (π/2 t) – 4/3π cos (3π/2 t)+ 4/5π cos(5π/2 t) - …………..
= 4/π [ cos(π/2 t) -1/ 3 cos( 3π/2 t ) + 1/5 cos (5 π/2 t) – 1/7 cos(7π/2 t) + ………..
2. Exponential Fourier Series
The exponential Fourier series is another form of Fourier series. Using Euler’s identity we cam write
An cos(Ω0nt + 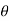 n ) = An [ ej(Ω0nt +
n ) = An [ ej(Ω0nt + 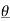 n) –e -j(Ω0nt +
n) –e -j(Ω0nt + 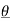 n)]
n)]
2
x(t) = A0 + 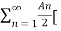 ej(Ω0nt +
ej(Ω0nt + 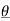 n) –e- j(Ω0nt +
n) –e- j(Ω0nt + 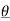 n)]
n)]
= A0 + 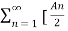 ej(Ω0nt ) ej
ej(Ω0nt ) ej 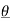 n) –e- j(Ω0nt ) . ej
n) –e- j(Ω0nt ) . ej 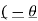 n)]
n)]
= A0 + 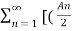 ej
ej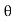 n ) ej(Ω0nt ) + (An/2 e-j
n ) ej(Ω0nt ) + (An/2 e-j 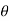 n ) e- j(Ω0t ) ] -------- (1)
n ) e- j(Ω0t ) ] -------- (1)
Let n=-k
x(t) = A0 + 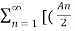 ej
ej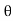 n ) ej(Ω0nt ] +
n ) ej(Ω0nt ] + 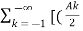 ej
ej 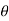 k ) e j(Ω0kt ) ------- (2)
k ) e j(Ω0kt ) ------- (2)
Comparing (1) and (2) we get
An = Ak (-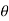 n ) =
n ) = 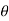 k n>0 k<0-------------------(3)
k n>0 k<0-------------------(3)
Let us define c0 = A0 ; cn =An/2 ej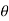 n for n>0
n for n>0
By changing the index from k to n and combining into one equation we get
x(t) = A0 + 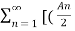 ej
ej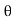 n ) ej(Ω0nt) +
n ) ej(Ω0nt) + 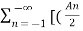 ej
ej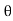 n) ej(Ω0nt)]
n) ej(Ω0nt)]
x(t) = 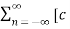 n ej(Ω0nt) ]
n ej(Ω0nt) ]
The above series is known as Exponential Fourier Series.
To develop the coefficients of the the exponential Fourier series
We know that
x(t) = 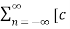 n ej(Ω0nt) ] where Ω0 = 2π/T
n ej(Ω0nt) ] where Ω0 = 2π/T
Multiply e-jk Ω0 t and integrate over one period .Then
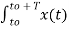 e-jk Ω0 t dt =
e-jk Ω0 t dt = 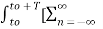 cn ej(Ω0nt) ] e-jk Ω0 t dt
cn ej(Ω0nt) ] e-jk Ω0 t dt
= 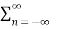 cn
cn 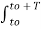 ej(Ω0nt) e-jk Ω0 t dt
ej(Ω0nt) e-jk Ω0 t dt
Substituting the relation 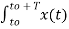 e-jk Ω0 t dt = 0 for k ≠n and T when k=n
e-jk Ω0 t dt = 0 for k ≠n and T when k=n
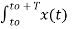 e-jk Ω0 t dt = T ck
e-jk Ω0 t dt = T ck
Therefore
Ck = 1/T 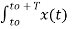 e-jk Ω0 t dt
e-jk Ω0 t dt
Or
Cn = 1/T 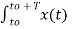 e-jk Ω0 t dt
e-jk Ω0 t dt
Where cn are the Fourier series coefficients of exponential Fourier series.
Problems:
- Compute the Exponential series of the following series.
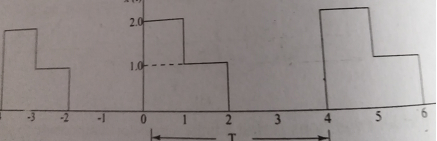
The time period of the signal x(t) isT=4.
Ω0 = 2π/T = 2 π/4= π/2
C0 = 1/T 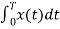 = ¼ [
= ¼ [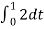 +
+ 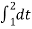
C0 = ¼ [ 2+1 ] = ¾
Cn = 1/T [ 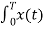 e-jnΩot dt = ¼[
e-jnΩot dt = ¼[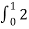 e-jnπ/2t dt +
e-jnπ/2t dt + 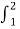 e-jn π/2t dt
e-jn π/2t dt
= ½ . 1/ -jn π/2 [e-jn π/2t ] 0 1 + ¼ 1/-jn π/2[ e-jn π/2t ] 1 2
= - 1/jn π[e-jn π/2 – 1] – 1/ 2jn π (e-jn π – e-jn π/2 )
= 1/jn π[ 1 - e-jn π/2 ] – 1/ 2 e-jn π + ½ e-jn π/2 )
= 1/jn π [ 1- ½ (-1) n -1/2 e-j n π/2 ]
3. Fourier Integral and Fourier Transform
Fourier Integral
The formula for the decomposition of a non-periodic function into harmonic components whose frequencies range over a continuous set of values.
If a function f(x) satisfies the Dirichlet condition on every finite interval and if the integral
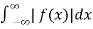 converges then
converges then
F(x) = 1/π 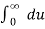
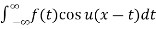 --------- (1)
--------- (1)
The formula was first introduced by J. Fourier in connection with the solution of certain heat conduction problems but was proved later by other mathematicians.
Formula(1) can also be given in the form
f(x) = 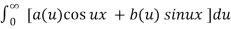 ------- (2)
------- (2)
Where
a(u) = 1/π 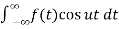
b(u) = 1/π 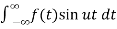
In particular for even functions
f(x) = 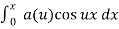 where
where
a(u) = 2/π 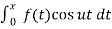
By taking the limits of Fourier series for functions with period 2T as T -> ∞
Then a(u) and b(u) are analogues of the Fourier coefficients of f(x)
Using complex numbers we can replace formula (1) with
f(x) = 1/2π 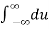
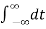 e ju(x-t) f(t)
e ju(x-t) f(t)
f(x)= lim 1/π 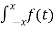 sin
sin 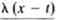 dt
dt
x-t
This is called Fourier Integral.
Problem:
1.Find the Fourier integral of
f(x) = |sin x| |x| ≤ π
= 0 |x| ≥ π
Deduce that 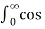 π +1/ 1 -
π +1/ 1 - 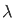 2 cos (
2 cos (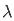 π/2) d
π/2) d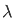 = π/2
= π/2
Solution:
f(x) = 2/π 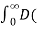
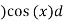
=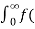 t
t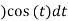 =
= 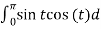
=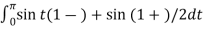
= - cost(1-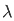 ) ]0 π - cost(1+
) ]0 π - cost(1+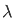 ) ]0 π
) ]0 π
2(1-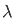 ) 2(1+
) 2(1+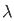 )
)
= 1/ 1- 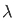 2 [cos π
2 [cos π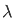 + 1]
+ 1]
=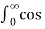 π +1/ 1 -
π +1/ 1 - 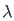 2 cos (
2 cos (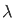 π/2) d
π/2) d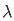 = π/2
= π/2
Find the Fourier Integral of
f(x) = 1 |x| ≤ 1
0 |x| ≥ 1
f(x) = 1/π 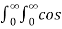
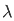 (t-x) dt d
(t-x) dt d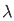
= 1/π 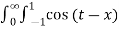 dt d
dt d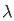
= 1/π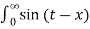 /
/ 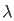 ] -1 1 d
] -1 1 d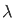
= 1/π 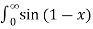 -
- 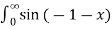 /
/ 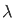 d
d 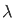
= 1/π 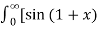 – sin
– sin 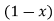 ]/
]/ 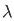 d
d 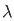
= 2/π 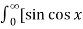 /
/ 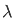 d
d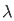 = π/2 when |x| < 1 and 0 when |x| >1
= π/2 when |x| < 1 and 0 when |x| >1
By setting x=0
= 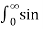 /
/ 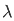 d
d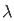 = π/2.
= π/2.
Fourier Transform
Consider a periodic signal f(t) with period T. The complex Fourier series representation of f(t) is given as
f(t) = 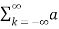 k ejkw0t
k ejkw0t
= 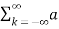 k ej2π/T0kt -------- (1)
k ej2π/T0kt -------- (1)
Let 1/T0 = 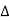 f then equation (1) becomes
f then equation (1) becomes
f(t) = 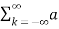 k ej2π
k ej2π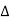 kft --------------- (2)
kft --------------- (2)
But you know that
Ak = 1/ T0 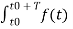 e-jkw0t dt
e-jkw0t dt
Substitute in eq(2)
f(t) = 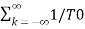
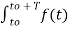 e-jkw0t dt ej2πk
e-jkw0t dt ej2πk 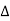 ft
ft
Let to = T/2 then
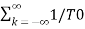
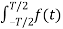 e-j2πkt
e-j2πkt  dt ej2πkt
dt ej2πkt  ft
ft  f
f
As lim T-> ∞  f approaches differential df, k
f approaches differential df, k 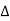 f becomes continuous variable hence summation becomes integration
f becomes continuous variable hence summation becomes integration
f(t) = lim T-> ∞ { 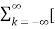
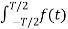 e-j2πk
e-j2πk 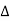 ft dt] ej2πk
ft dt] ej2πk 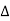 ft
ft  f
f
= 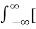
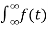 e-j2π ft dt] ej2π ft df
e-j2π ft dt] ej2π ft df
f(t)= 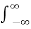
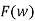 ejwt dw
ejwt dw
Where F(w) = 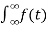 e-j2π ft dt
e-j2π ft dt
Fourier transform of a signal is given by
f(t) = F(w) = 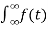 e-jwt dt
e-jwt dt
And Inverse Fourier transform is given by
f(t) = 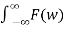 ejwt dw
ejwt dw
Fourier transform are classified into
- Continuous Fourier transform and
- Discrete Fourier transform.
Continuous Fourier Transform
Fourier series was defined for periodic signals. A periodic signals can be considered as a periodic signal with fundamental period
Consider a periodic square wave:
x(t) = 1 for |t| < T1
= 0 T1 < |t| < T0/2
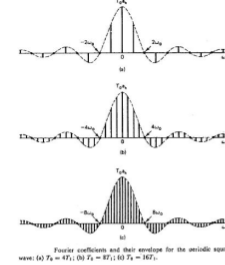
The fourier series co-efficient is
Ak = 2 sin(kwoT1)
k wo T0
To.ak = 2 sin(wT1) | w=kw0
w
Discrete Fourier Transform
The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.
The DTFT sequence x[n] is given by
X(w) = 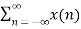 e-jwn ---------------(1)
e-jwn ---------------(1)
Here X(w) is a complex function of real frequency variable w and can be written as
X(w) = Xre (w) + j X img(w)
Where Xre (w) , j X img(w) are real and Imaginary parts of X(w)
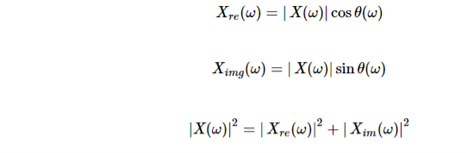
And | X(w)| can be represented as
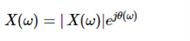 .
.
Inverse Discrete Fourier Transform is given by
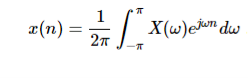
Problems:
Find the four point DFT of the sequence
x(n) = {0,1,2,3}
Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1 for n=0
W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j
W42 = e-j π = cos π – j sin π = -1
W43 = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j
For k=0
X(k) = 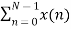 e-j2 π nk/N
e-j2 π nk/N
X(0) =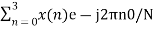
X(0) = x(0)+ x(1)+x(2) + x(3) = 0 +1+2+3 = 6
X(1) = 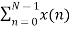 e-j2 π nk/N
e-j2 π nk/N
X(1) = 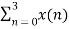 e-j2 π n/4
e-j2 π n/4
= x(0) e0 + x(1) e –j2 π /4+ + x(2) e-j4 π/4+ x(3) e- j 6 π/4
= 0 + 1 –j + 2( -1) + 3(j)
= -2+ 2j
X(2) = 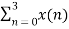 e-j2 π n2/4
e-j2 π n2/4
X(2) = 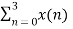 e-j π n
e-j π n
X(2) = x(0) 1+ x(1) e-j π + x(2) e-j2 π + x(3) e-j3 π
X(2) = -2
X(3) = 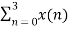 e-j2 π n3/4
e-j2 π n3/4
X(3) = x(0) e0 + x(1) e-j3 π/2 + x(2) e-j3 π + x(3) e-j9 π/2
X(3) = -2-2j.
DFT = { 6, -2+2j,-2,_2-2j}
Properties of Fourier Transform
Linear Property
If x(t) -> X(w)
Y(t) -> Y(w) then
a x(t) + b y(t) -> a X(w) +b Y(w)
Time Shifting Property
If x(t)⟷F.TX(ω)
Then Time shifting property states that
x(t−t0)⟷F.T e−jω0t X(ω)
Frequency Shifting Property
If x(t)⟷X(ω)
Then frequency shifting property states that
Ejω0t.x(t)⟷X(ω−ω0)
Time Reversal Property
If x(t)⟷X(ω)
Then Time reversal property states that
x(−t)⟷X(−ω)
Differentiation Property
If x(t)⟷X(ω)
Then Differentiation property states that
Dx(t)dt⟷jω.X(ω)
dnx(t)dtn⟷(jω)n.X(ω)
Integration Property
Integration property states that
∫x(t)dt⟷1jω X(ω)
Then
∭...∫x(t)dt⟷(jω)n X(ω)
Multiplication and Convolution Properties
If x(t)⟷X(ω)
y(t)⟷Y(ω)
Then multiplication property states that
x(t).y(t)⟷X(ω)∗Y(ω)
And convolution property states that
x(t)∗y(t)⟷1/2πX(ω).Y(ω)
4. Analysis by Fourier Methods
There are multiple Fourier methods that are used in signal processing.
The most common are
- Fourier transform,
- Discrete-time Fourier transform,
- Discrete Fourier transform,
- Short-time Fourier transform.
Fourier methods are used for two primary purposes:
- Mathematical analysis of problems
- Numerical analysis of data.
- The Fourier transform and discrete-time Fourier transform are mathematical analysis tools and cannot be evaluated exactly in a computer.
- The Fourier transform is used to analyze problems involving continuous-time signals or mixtures of continuous- and discrete-time signals.
- The discrete-time Fourier transform is used to analyze problems involving discrete-time signals or systems.
- In contrast, the discrete Fourier transform is the computational workhorse of signal processing. It is used solely for numerical analysis of data.
- Lastly, the short-time Fourier transform is a variation of the discrete Fourier transform that is used for numerical analysis of data whose frequency content changes with time.
DTFT
The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.
The DTFT sequence x[n] is given by
X(w) = 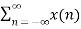 e-jwn ---------------(1)
e-jwn ---------------(1)
Here X(w) is a complex function of real frequency variable w and can be written as
X(w) = Xre (w) + j X img(w)
Where Xre (w) , j X img(w) are real and Imaginary parts of X(w)
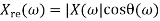
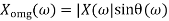
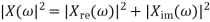
And | X(w)| can be represented as
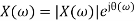 .
.
Inverse Discrete Fourier Transform is given by
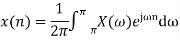
Problems:
Find the four point DFT of the sequence
x(n) = {0,1,2,3}
Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1 for n=0
W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j
W42 = e-j π = cos π – j sin π = -1
W43 = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j
For k=0
X(k) = 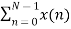 e-j2 π nk/N
e-j2 π nk/N
X(0) =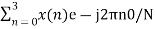
X(0) = x(0)+ x(1)+x(2) + x(3) = 0 +1+2+3 = 6
X(1) = 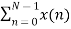 e-j2 π nk/N
e-j2 π nk/N
X(1) = 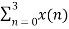 e-j2 π n/4
e-j2 π n/4
= x(0) e0 + x(1) e –j2 π /4+ + x(2) e-j4 π/4+ x(3) e- j 6 π/4
= 0 + 1 –j + 2( -1) + 3(j)
= -2+ 2j
X(2) = 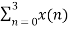 e-j2 π n2/4
e-j2 π n2/4
X(2) = 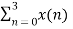 e-j π n
e-j π n
X(2) = x(0) 1+ x(1) e-j π + x(2) e-j2 π + x(3) e-j3 π
X(2) = -2
X(3) = 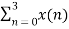 e-j2 π n3/4
e-j2 π n3/4
X(3) = x(0) e0 + x(1) e-j3 π/2 + x(2) e-j3 π + x(3) e-j9 π/2
X(3) = -2-2j.
DFT = { 6, -2+2j,-2,_2-2j}
Frequency domain sampling
Sampling in frequency domain is usually used in DFT (Discrete Fourier transform), where continuous signal of spectrum in sampled to get discrete values of spectrum, which results in periodicity in time domain. This helps to process any continuous spectrum signal of non periodic in nature to discretize and digitize for further processing.
DFT
The discrete Fourier transform transforms a sequence of N complex numbers 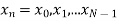 into another sequence of complex numbers
into another sequence of complex numbers
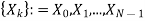 which is defined by
which is defined by
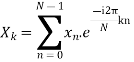
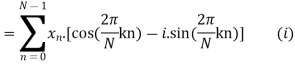
Example:
Let N =4 and
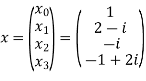
Here we demonstrate how to calculate the DFT of x using equation (1)
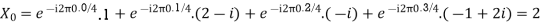
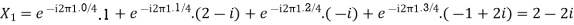
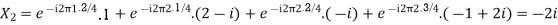
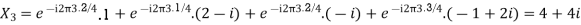
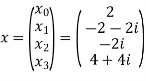
Properties of DFT
Linear Property
If x(t) -> X(w)
Y(t) -> Y(w) then
a x(t) + b y(t) -> a X(w) +b Y(w)
Time Shifting Property
If x(t)⟷F.TX(ω)
Then Time shifting property states that
x(t−t0)⟷F.T e−jω0t X(ω)
Frequency Shifting Property
If x(t)⟷X(ω)
Then frequency shifting property states that
Ejω0t.x(t)⟷X(ω−ω0)
Time Reversal Property
If x(t)⟷X(ω)
Then Time reversal property states that
x(−t)⟷X(−ω)
Differentiation Property
If x(t)⟷X(ω)
Then Differentiation property states that
Dx(t)dt⟷jω.X(ω)
dnx(t)dtn⟷(jω)n.X(ω)
Integration Property
Integration property states that
∫x(t)dt⟷1jω X(ω)
Then
∭...∫x(t)dt⟷(jω)n X(ω)
Multiplication and Convolution Properties
If x(t)⟷X(ω)
y(t)⟷Y(ω)
Then multiplication property states that
x(t).y(t)⟷X(ω)∗Y(ω)
And convolution property states that
x(t)∗y(t)⟷1/2πX(ω).Y(ω)
Numericals:
- Compute the N-point DFT of x(n)=3δ(n).
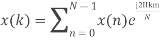
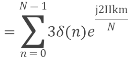
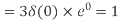
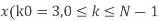
2. Compute the N-point DFT of x(n)=7(n−n0)
Solution − We know that,
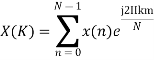
Substituting the value of x(n),
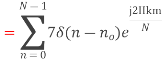
Circular convolution
Let us take two finite duration sequences 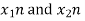 ,having integer length as N. Their DI are
,having integer length as N. Their DI are 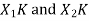 reapectively which is shown below
reapectively which is shown below
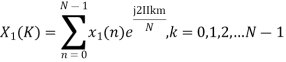
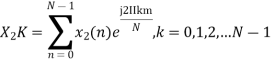
Now we will try to find the DFT of another sequence 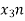 , which is given by
, which is given by 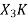
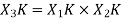
By taking the IDFT of the above we get
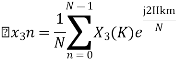
After solving the above equation finally we get
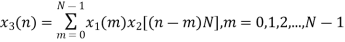
Methods of Circular Convolution
Generally, there are two methods, which are adopted to perform circular convolution and they are −
- Concentric circle method,
- Matrix multiplication method.
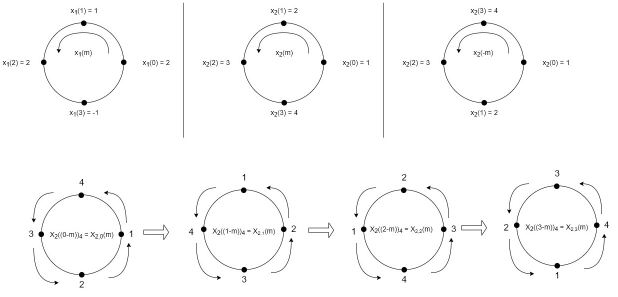
Concentric Circle Method
Let x1(n) and x2(n) be two given sequences. The steps followed for circular convolution of x1(n) and x2(n) are
- Take two concentric circles. Plot N samples of x1(n) on the circumference of the outer circle maintaining equal distance successive points maintaining equal distance successive points in anti-clockwise direction.
- For plotting x2(n), plot N samples of x2(n) in clockwise direction on the inner circle, starting sample placed at the same point as 0th sample of x1(n)
- Multiply corresponding samples on the two circles and add them to get output.
- Rotate the inner circle anti-clockwise with one sample at a time.
Matrix Multiplication Method
Matrix method represents the two given sequence x1(n) and x2(n) in matrix form.
- One of the given sequences is repeated via circular shift of one sample at a time to form a N X N matrix.
- The other sequence is represented as column matrix.
- The multiplication of two matrices give the result of circular convolution.
Numerical:
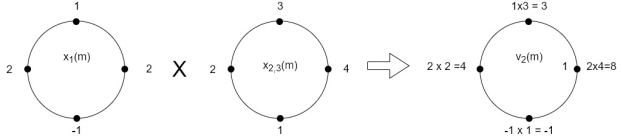
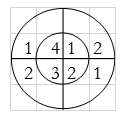
Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}
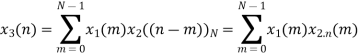
(2)
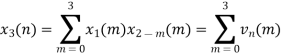
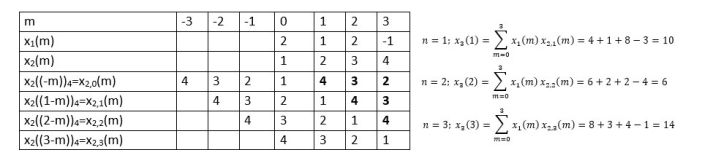
When n=0; 
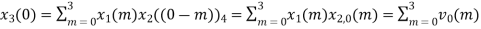
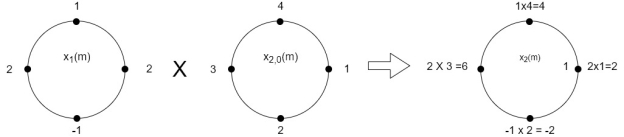
The sum of samples of v0(m) gives x3(0)
⸫ x3(0)=2+4+6-2=10
When n=1; 
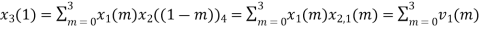
The sum of samples of v1(m) gives x2(1)
⸫ x3(1)=4 + 1 +8-3=10
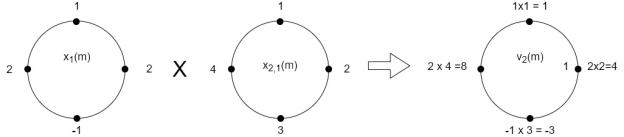
(3)When n=2; 
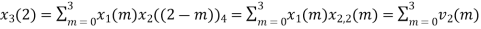
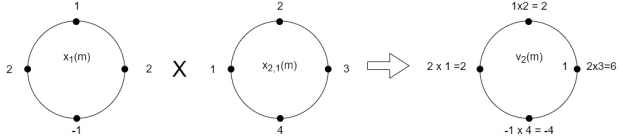
The sum of samples of v2(m) gives x3(2)
⸫ x3(2)=6+2+2-4=6
(4) When n=3; 
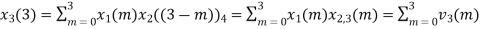
The sum of samples of v3(m) gives x3(3)
⸫ x3(3)=8+ 3+ 4-1= 14
x3(n)={10,10,6,14}
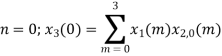
= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)
= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10
Linear convolution
Linear Convolution states that
y(n) = x(n) * h(n)
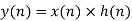
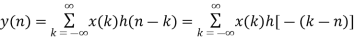
Example 1: h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n).
METHOD 1: GRAPHICAL REPRESENTATION
Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n))
Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1



METHOD 2: MATHEMATICAL FORMULA
Use Convolution formula
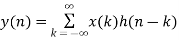
k= 0 to 3 (start index to end index of x(n))
y(n) = x(0) h(n) + x(1) h(n-1) + x(2) h(n-2) + x(3) h(n-3)
METHOD 3: VECTOR FORM (TABULATION METHOD)
X(n)= {x1,x2,x3} & h(n) ={ h1,h2,h3}

y(-1) = h1 x1
y(0) = h2 x1 + h1 x2
y(1) = h1 x3 + h2x2 + h3 x1 …………
METHOD 4: SIMPLE MULTIPLICATION FORM
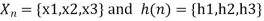
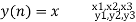
Computation of linear convolution using circular convolution
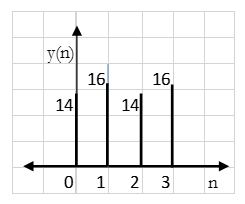
Find circular convolution and linear using circular convolution for the following sequences x1(n) = {1, 2, 3, 4} and x2(n) = {1, 2, 1, 2}. Using Time Domain formula method.
Solution:
Circular convolution using circular convolution:
x1x1(n) = {1, 2, 3, 4}
And x2x2 (n) = {1, 2, 1, 2}
L=4, M=4
Length of y(n) = L+M-1=4+4-1=7
∴,x1(n) = {1, 2, 3, 4, 0, 0, 0}
& x2(n) = {1, 2, 1, 2, 0, 0, 0}
For y(0),
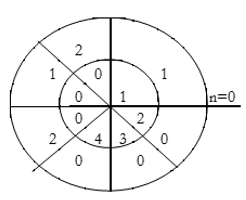
∴ y(0)= 1×1=1
For y(1),
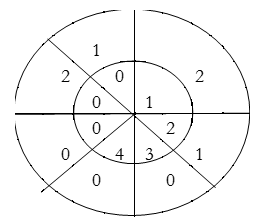
∴ y(1)= 2×1+1×2=4
For y(2),
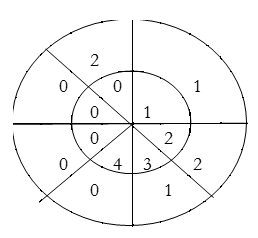
∴ y(2)= 1×1+2×2+3×1=8
For y(3),
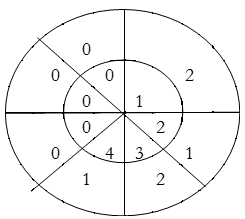
y(3)=1×2+2×1+3×2+4×1=14
For y(4),
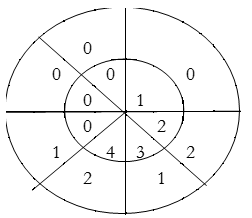
∴ y(4)= 4×2+3×1+2×2=15
For y(5),
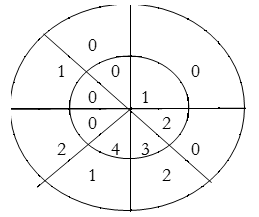
∴ y(5) = 4×1+3×2=10
For y(6),
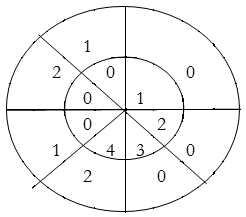
∴ y(6) = 4×2=8
∴y(n) = {1, 4, 8, 14, 15, 10, 8}
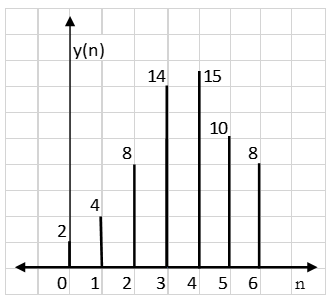
Result: y(n) = {2, 4, 8, 14, 15, 10, 8}
Linear using circular convolution:
For y(0),
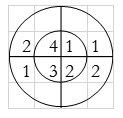
∴ y(0)= 1+4+3+8=16
For y(1),
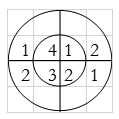
∴ y(1)= 2+2+6+4=14
For y(2),
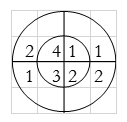
∴ y(2)= 1+4+3+8=16
For y(3),
∴ y(3)= 2+2+6+4=14
y(n) = {16, 14, 16, 14}
Result: y(n) = {14, 16, 14, 16}
2.8 FFT
Certain algorithms permit implementations of Discrete Fourier transform with considerable savings in computation time. These algorithms are known as Fast Fourier Transform.
FFT algorithm are based on fundamental principle of decomposing the computation of DFT of sequence length into successively smaller discrete Fourier transforms.
They are basically two classes of FFT algorithms
- Decimation in time
- Decimation in frequency
Decimation in time and decimation in frequency using Radix-2 FFT algorithm
Decimation-in-time algorithm
This algorithm is known as Radix-2 DIT-FFT algorithm which means the number of output points N can be expressed as a power of 2 that is N = 2M where M is an integer.
Let x(n) be a sequence where N is assumed to be a power of 2. Decimate or break this sequence into two sequences of length N/2 where one sequence consists of even-indexed values of x(n) and the other of odd-indexed values of x(n).
Xe(n) = x(2n) n= 0,1,……….. N/2-1
Xo(n) = x(2n+1) n= 0,1,……….. N/2 -1
The N-pt DFT of x(n) can be written as
X(k) = 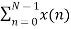 WN nk where k=0,1……….. N-1.
WN nk where k=0,1……….. N-1.
Separating x(n) into even and odd indexed values of x(n) we obtain
X(k) = 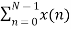 WN nk +
WN nk + 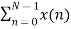 WN nk
WN nk
( n even) (n odd)
= 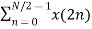 WN 2nk +
WN 2nk +  WN (2n+1)k
WN (2n+1)k
= 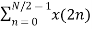 WN 2nk + Wnk
WN 2nk + Wnk 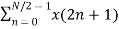 W N 2nk
W N 2nk
X(k) = 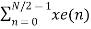 WN 2nk + Wnk
WN 2nk + Wnk 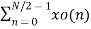 W N 2nk
W N 2nk
WN2 =( e-j2π/N) 2 = e-j2π/N/2 = W N/2 .
WN2 = W N/2
X(k) = 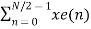 W N/2n k + WNk
W N/2n k + WNk 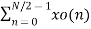 WN/2kn
WN/2kn
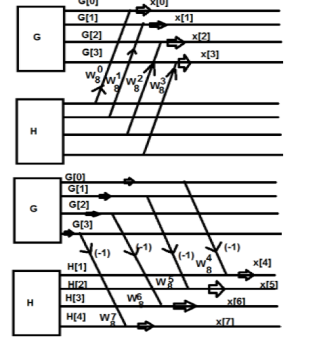
W84 = -1
W8 5 = - W 81
W86 = - W82
W87 = - W83
G(0) – H(0) = x(4)
G(1) - W 81 H(1) = x(5)
G(2) - W82 H(2) = x(6)
G(3) - W83 H(3) = x(7)
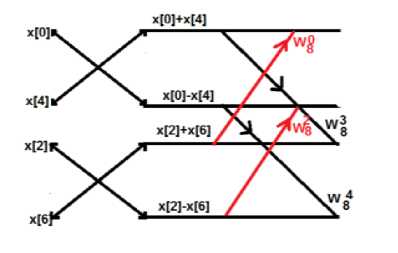
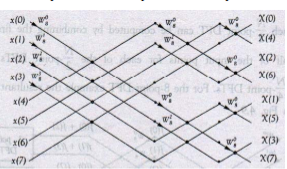
Consider the sequence x[n]={ 2,1,-1,-3,0,1,2,1}. Calculate the FFT.
Arrange the sequence as x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7)
Since N=8 find the values W8 0 to W 87
Apply the butterfly diagram to obtain the values.
Decimation in Frequency FFT
Apart from time sequence, an N-point sequence can also be represented in frequency. Let us take a four-point sequence to understand it better.
Let the sequence be x[0],x[1],x[2],x[3]………..x[7]
Mathematically, this sequence can be written as;
X(k) = 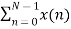 WN n-k where k=0,1……….. N-1.
WN n-k where k=0,1……….. N-1.
Now let us make one group of sequence number 0 to 3 and another group of sequence 4 to 7. Now, mathematically this can be shown as
= 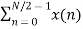 WN nk +
WN nk + 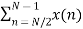 WN nk
WN nk
Let us replace n by r, where r = 0, 1 , 2….N/2−1.
= 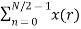 W N/2 nr
W N/2 nr
We take the first four points x[0],x[1],x[2],x[3] initially, and try to represent them mathematically as follows –
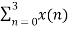 W 8 nk +
W 8 nk + 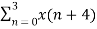 W8 (n+4) k
W8 (n+4) k
= 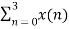 +
+ 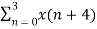 W8 (n+4) k
W8 (n+4) k
= 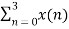 + {
+ { 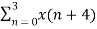 W8 (4) k } W8 nk
W8 (4) k } W8 nk
X[0] = 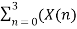 + X[n+4]
+ X[n+4]
X[1] = 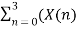 + X[n+4]) W8 nk
+ X[n+4]) W8 nk
= X(0) – X(4) + (x[1] – X[5]) W8 1 + ( X[2] – X[6] )W82 + X(3) – X(7) W8 3
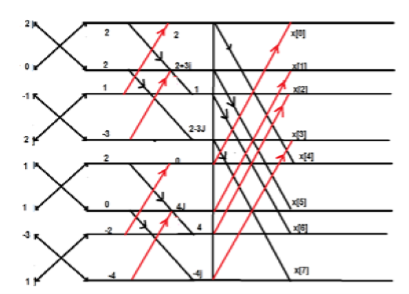
DIF –FFT Algorithm
Find the DIF –FFT of the sequence x(n)= { 1,-1,-1,1,1,1,-1} using Dif-FFT algorithm.
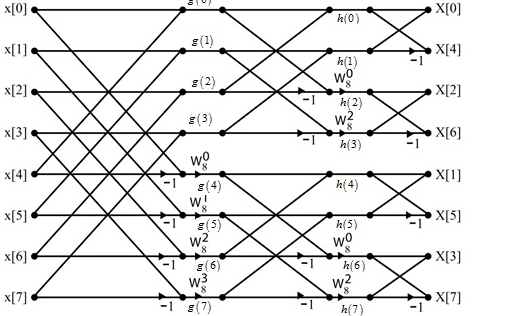
X(0)= 20 X(4) =0
X(1) = -5.828- j2.414 X(5) = -0.1716 + j 0.4141
X(2) = 0 X(6) = 0
X(3) = -0.171 – j 0.4142 X(7) = -5.8284 + j2.4142
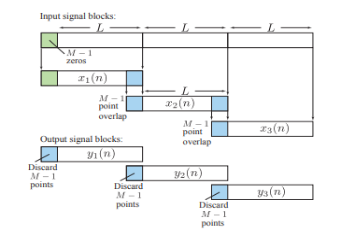
Linear filtering using overlap add and overlap save method
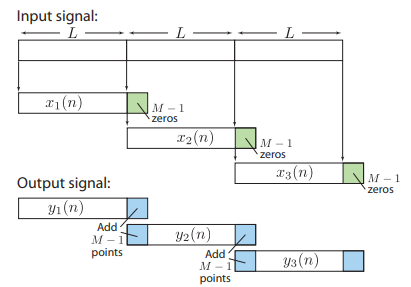
Overlap add method
- Break the input signal x(n) into non overlapping blocks
 of length L.
of length L. - Zero pad h(n) to be of length N=L+M-1.
- Take N-DFT of h(n) to give H(k), k = 0,1,…,N-1.
- Fop each block m
- Zero pad
 to be length of N-L+M-1.
to be length of N-L+M-1. - Take N-DFT of
 to give
to give 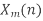 , k=0,1,…,N-1.
, k=0,1,…,N-1. - Multiply
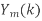 =
=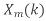 . H(k), k=0,1,…,N-1.
. H(k), k=0,1,…,N-1. - Take N-DFT of
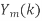 to give
to give 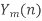 , n=0,1,…,N-1.
, n=0,1,…,N-1.
- Zero pad
- Form y(n) by overlapping the last M-1 samples of
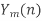 with the first M-1 samples of
with the first M-1 samples of 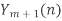 and adding the result.
and adding the result.
Overlap save method
- Insert M-1 zeros at the beginning of the input sequence x (n).
- Break the padded input signal into overlapping blocks
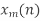 of length N = L +M-1 where the overlap length is M-1.
of length N = L +M-1 where the overlap length is M-1. - Zero pad h (n) to be of length N = L+M-1.
- Take N-DFT of h (n) to give H (k), k= 0,1,…,N-1.
- For each block m\
- Take N-DFT of
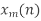 to give
to give 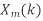 , k= 0,1,…,N-1.
, k= 0,1,…,N-1. - Multiply
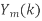 =
= 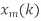 . H (k), k=0,1,…,N-1.
. H (k), k=0,1,…,N-1. - Take N-DFT of
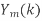 to give
to give 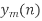 , n=0,1,…,N-1.
, n=0,1,…,N-1. - Discard the first M-1 points of each output block
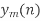 .
.
- Take N-DFT of
- Form y (n) by appending the remaining i.e. last L samples of each block
 .
.
Introduction to Discrete Cosine Transform
The discrete cosine transform (DCT) helps separate the image into parts (or spectral sub-bands) of differing importance (with respect to the image's visual quality). The DCT is similar to the discrete Fourier transform: it transforms a signal or image from the spatial domain to the frequency domain.
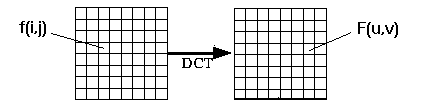
DCT Encoding
The general equation for a 1D (N data items) DCT is defined by the following equation:
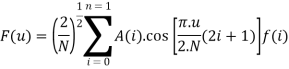
And the corresponding inverse 1D DCT transform is simple F-1(u), i.e.:
Where
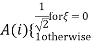
The general equation for a 2D (N by M image) DCT is defined by the following equation:
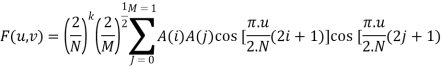
And the corresponding inverse 2D DCT transform is simple F-1(u,v), i.e.:
Where